2. 武警黄金第10支队, 昆明市, 650111
随着GNSS的广泛运用,在要求高精度、时效性的同时,服务模式的简化、服务产品的简单表达也引起广泛关注。传统的卫星钟差数据主要来自于卫星传输的导航文件和IGS钟差产品,均以数据序列的形式提供,采样率为30 s、5 min、15 min不等[1]。高采样率的钟差序列数据量大,对传输服务和数据利用造成负担。如果能利用数学模型分析钟差数据,并将其模型化,就能用简单的几个参数代替大量数据序列,在保证卫星定位精度不受影响的同时,简化卫星钟差长期以来的服务模式。
国内外学者在钟差函数模型方面的研究集中于多项式模型、Kalman滤波模型[2]、灰色模型[3]、ARIMA模型[4]、谐分析[5-8]及各种模型的组合等方面。多次项模型计算简单,但无法表达钟差的非平稳特性。本文选择多项式模型和结合周期项的混合函数模型对卫星钟差进行模型化和精度评估,将模型化后的钟差应用于PPP进行解算,评估不同模型化钟差的定位结果。
1 数学模型本文选择多项式模型以及结合周期项的混合函数模型。采用单天的IGS高精度卫星钟差产品进行模型参数的求解。多项式模型表示为:
| $ {\rm{clks}}\left( t \right) = \sum\limits_{n = 0}^l {\left( {{a_n} \times {t^n}} \right)} $ | (1) |
式中,an是n次多项式的系数,l是多项式函数的最高次数,t是历元数。多项式模型和Kalman滤波[2]、灰色模型[3]等类似,适合描述卫星钟差中稳定的趋势项,但对于其中的非平稳特性,其表达能力明显减弱。本文以多项式模型作为趋势项的基础,加上周期项部分,形成基于谐函数的混合函数模型:
| $ \begin{array}{l} {\rm{clks}}\left( t \right) = \sum\limits_{n = 0}^l {\left( {{a_n} \times {t^n}} \right)} + \\ \sum\limits_{i = 1}^k {{\lambda _i} \times \sin \left( {\frac{{2{\rm{ \mathsf{ π} }}}}{{{T_i}}} \times t + {\theta _i}} \right)} \end{array} $ | (2) |
式中,Ti为对应周期项的周期,λi、θi为对应周期项的振幅和相位。周期项的周期选择通过对多次项拟合残差进行频谱分析得到[7-8],文献[8-9]利用傅里叶变换进行频谱分析后,对Block ⅡF之前的系列卫星均探测出有4种谐波频率的周期性信号,频率约为每天(协调世界时每24 h)k×(2.002 9±0.000 5)周,其中k=1,2,3,4[6]。由于周期性变化和卫星轨道周期存在明显联系,本文认为该结论同样适用于Block ⅡF系列卫星。对于式(2),选择k=4,T1=12 h,T2=6 h,T3=4 h,T4=3 h。
2 模型化精度分析采用GPS周1 891~1 894共计28 d(2016-04-03~04-30)的IGS最终卫星钟差产品进行模型化研究,数据采样率为30 s。利用线性模型、二次多项式模型、三次多项式模型、二次多项式结合周期项的混合模型、三次多项式结合周期项的混合模型共5种模型,对每24 h(2 880历元)钟差数据进行模型化研究,采用函数模型进行对应系数的求解,并进行对应模型精度分析。
为了评估不同卫星的模型拟合效果,以G01(Block ⅡF Rb钟)、G05(Block ⅡR-M Rb钟)、G19(Block ⅡR Rb钟)、G24(Block ⅡF Cs钟)为例,所对应的每日RMS如图 1~4所示。

|
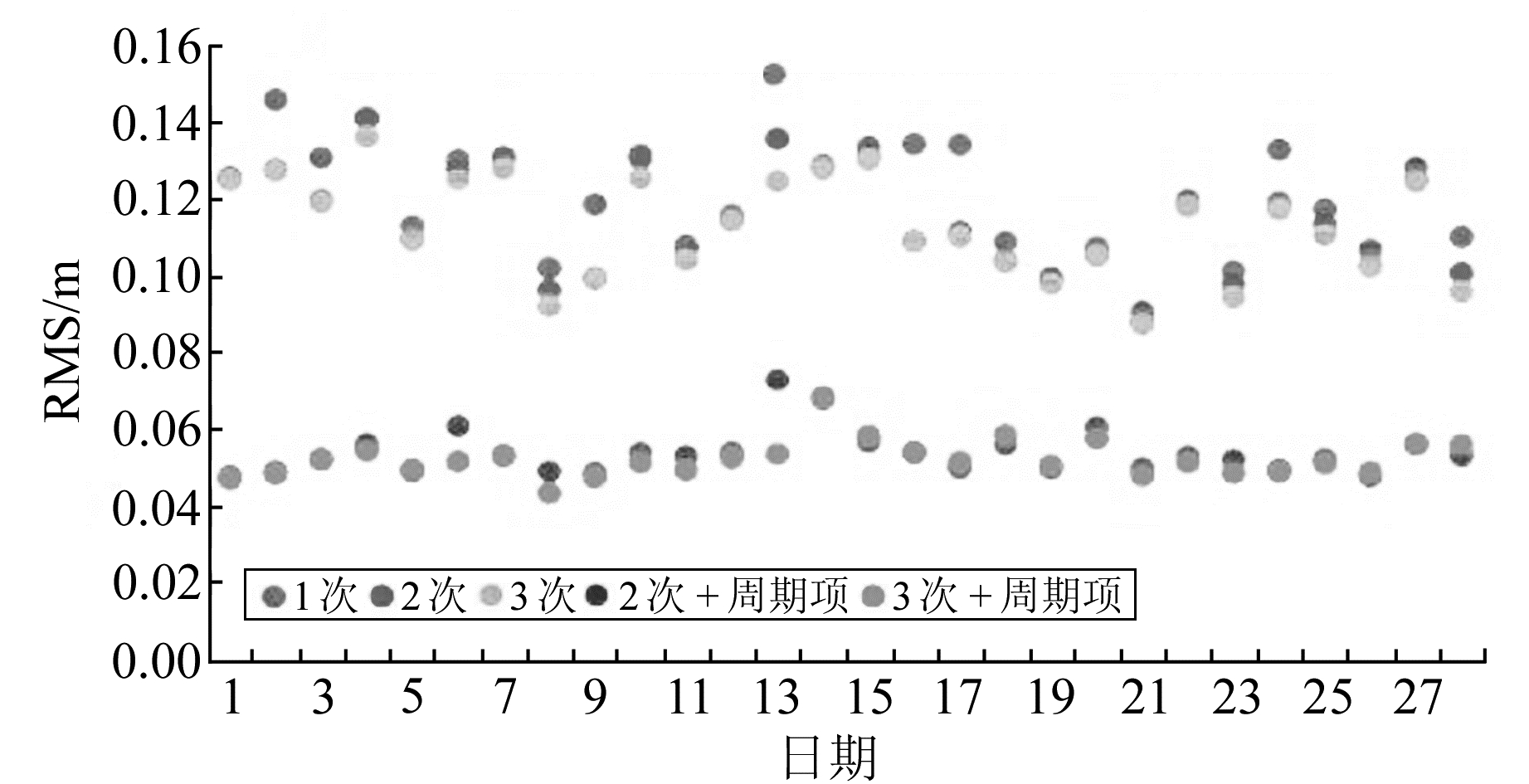
图 1 G01(Block ⅡF Rb钟)对应的每日RMS Fig. 1 RMS of G01(Block ⅡF Rb clock) |
|
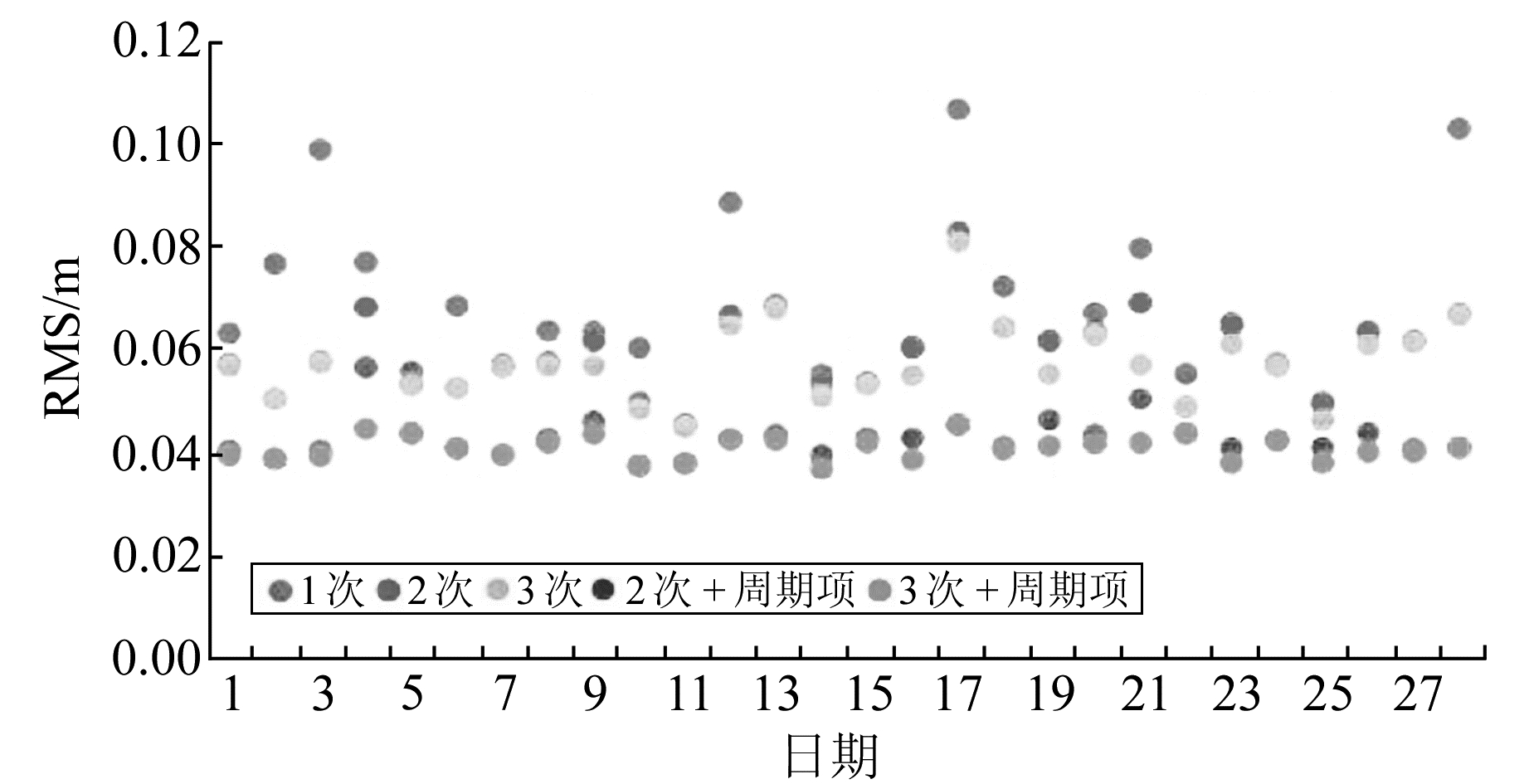
图 2 G05(Block ⅡR-M Rb钟)对应的每日RMS Fig. 2 RMS of G05(Block ⅡR-M Rb clock) |
|
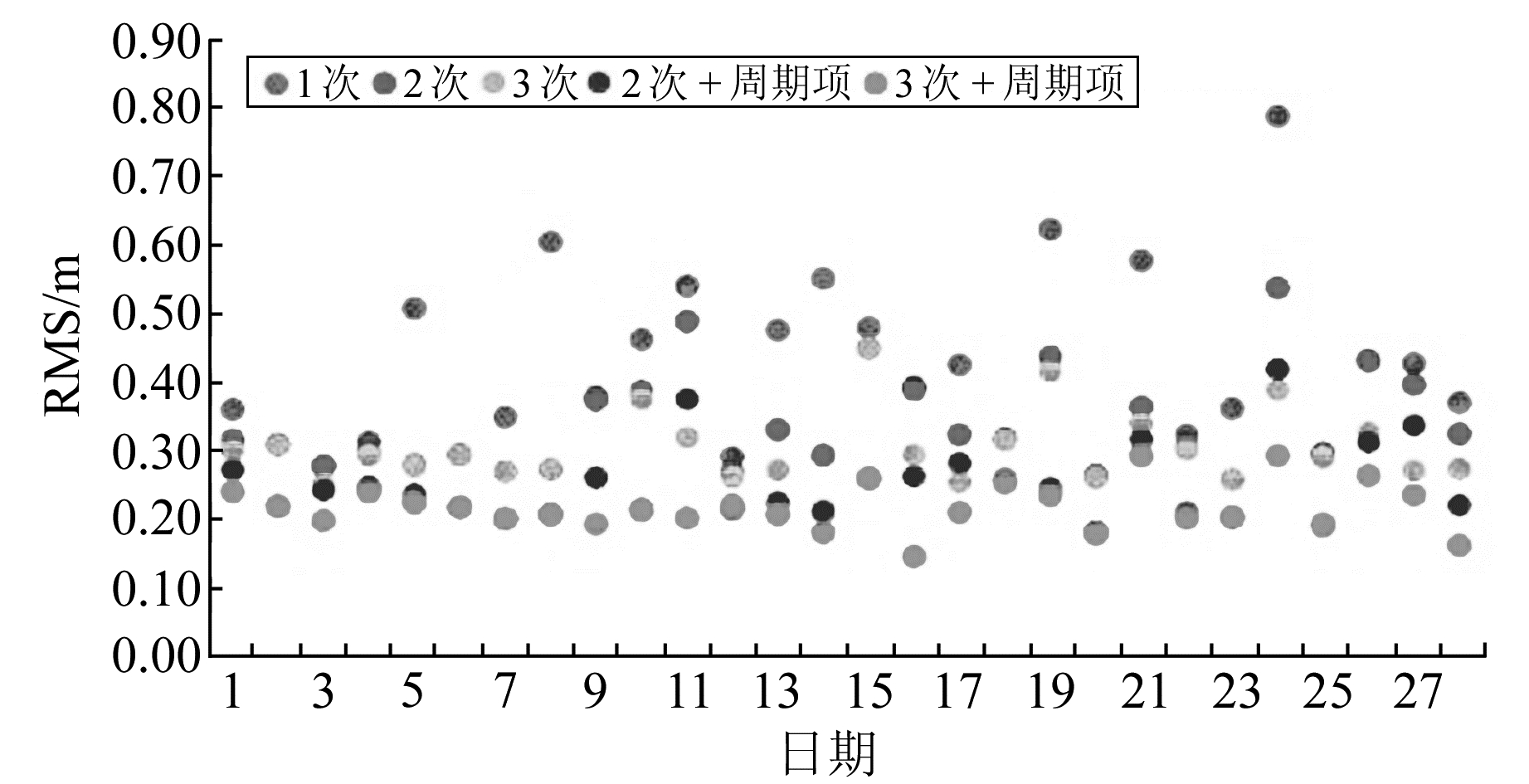
图 3 G19(Block ⅡR Rb钟)对应的每日RMS Fig. 3 RMS of G19(Block ⅡR Rb clock) |
|
图 4 G24(Block ⅡF Cs钟)对应的每日RMS Fig. 4 RMS of G24(Block ⅡF Cs clock) |
从图 1~4可看出,在只使用多项式模型的情况下,模型化精度随次数增大而提高,其中三次多项式模型精度略优于二次多项式,意味着至少对于24 h的钟差序列而言,提高多次项的项数,能够更好地拟合出钟差的变化特性。相比之下,结合周期项的混合函数模型的钟差模型化精度得到明显提高,证明混合函数模型比单纯的多次项模型更能表达出钟差的周期性变化。由图 1知,G01(Rb钟)的多项式模型化精度在0.05 m(约0.2 ns)左右,混合模型化精度提高到0.03 m(约0.1 ns)左右。由图 2、图 3知,G05(Rb钟)和G19(Rb钟)的多项式模型化精度在0.15 m(约0.5 ns)左右,混合模型化精度提高到0.05 m(约0.2 ns)左右。由图 4知,G24(Cs钟)的整体精度比Rb钟低一个量级,处于dm级(约ns级),和已有结论一致[10-11]。
不同类型卫星钟的钟差模型化精度存在差异,主要原因是各卫星发射年限及不同类型卫星性能有所区别。图 5为截至2016-04-03,4种不同类型卫星的平均运行时间。

|
图 5 在轨卫星运行时长 Fig. 5 The running time of the on-orbit satellite |
利用前述模型化后的卫星钟差和IGS精密星历及卫星轨道产品进行PPP解算。以2016-04-30结果为例,随机选择5个IGS观测站(WTZZ、WTZS、GUUG、WUHN、SHAO),对比不同卫星钟差PPP静态定位的解算结果。以IGS精密钟差解算结果的最终收敛值为基准,以测站WTZZ为例,图 6~8展示了不同的模型化钟差的PPP结果在站心坐标系E、N、U方向上随时间变化的差值。

|
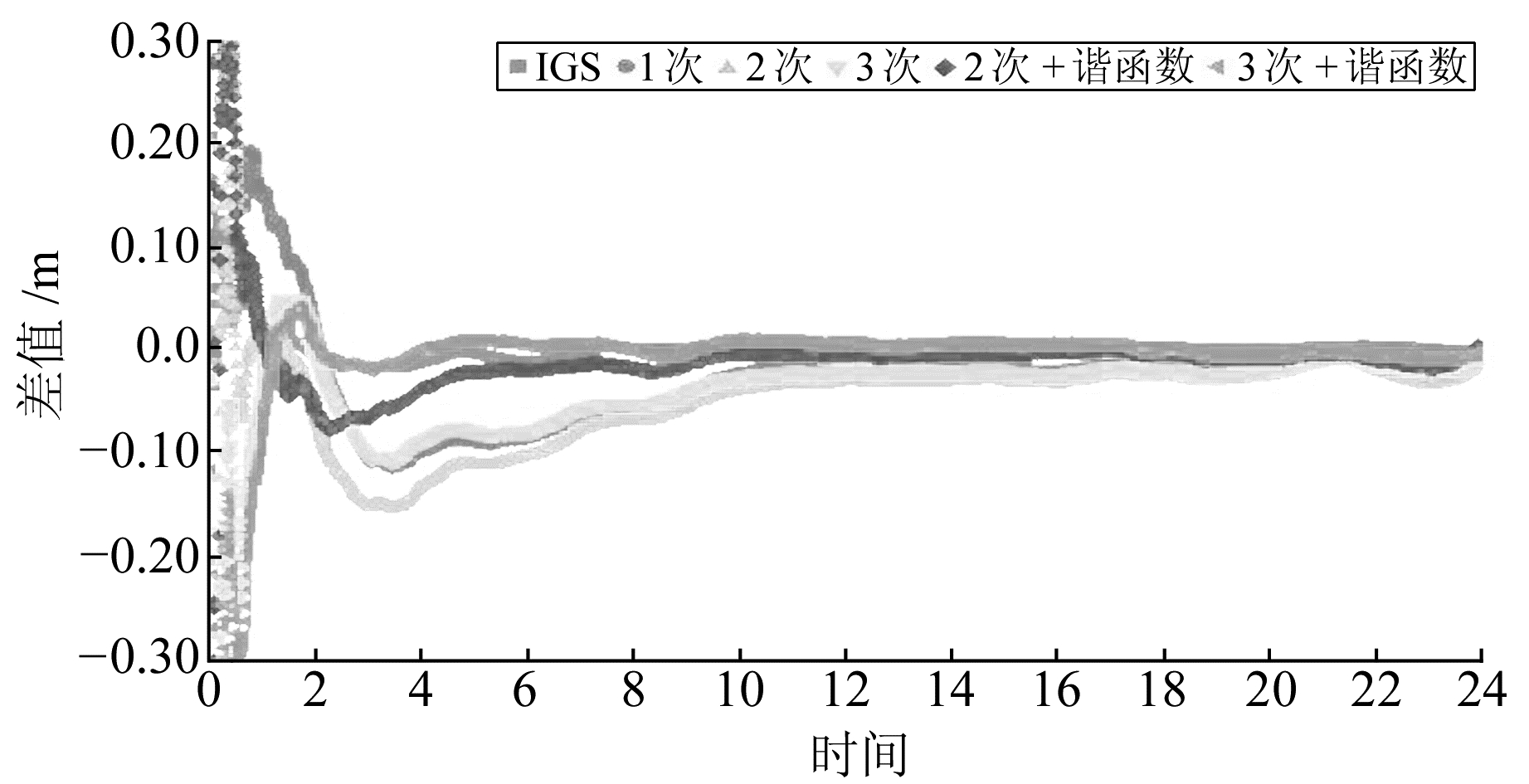
图 6 不同钟差定位结果在测站WTZZ的E方向上的偏差 Fig. 6 Effect of the satellite errors on the east direction of WTZZ |
|
图 7 不同钟差定位结果在测站WTZZ的N方向上的偏差 Fig. 7 Effect of the satellite errors on the north direction of WTZZ |
|
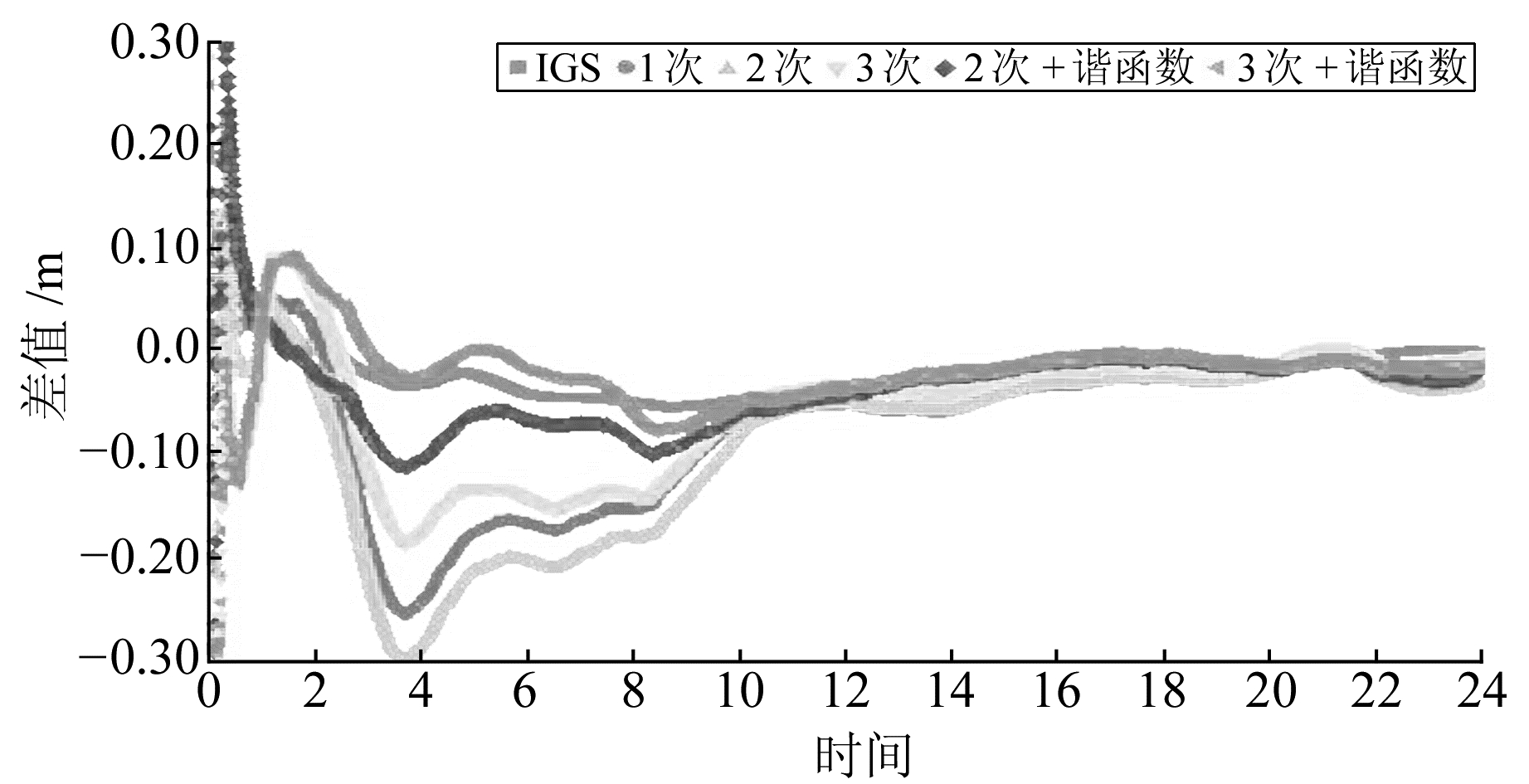
图 8 不同钟差定位结果在测站WTZZ的U方向上的偏差 Fig. 8 Effect of the satellite errors on the up direction of WTZZ |
由图 6~8可知,IGS精密钟差解算的定位结果最优,所有模型化钟差PPP结果的最终收敛值在各个方向均达到cm级。相比之下,结合周期项的混合函数模型化钟差比多项式模型化钟差的PPP结果精度更高、差值更小。
不同钟差在PPP解算的收敛时间以连续定位结果与最终收敛值不超过0.10 m为收敛标准。由图 9和表 1(单位h)可看出,IGS精密钟差收敛时间最短,在测站的3个方向上均于0.5 h左右收敛;结合周期项的混合函数模型化钟差的PPP收敛时间约为4 h,其中3次多项式结合周期项的混合函数模型化钟差表现较优;多项式模型化钟差的PPP收敛速度最慢,所需时间约为10 h。

|
图 9 测站WTZZ上不同钟差PPP解算的收敛时间 Fig. 9 PPP convergence time of different satellite clock errors of WTZZ |
|
|
表 1 不同钟差结果对应的参数收敛时间 Tab. 1 Convergence time of different satellite clock errors |
本文提出对卫星钟差进行模型化,并进一步使用简单参数代替数据序列,以达到简化卫星钟差服务的目的。选择多项式模型和结合周期项的混合函数模型进行24 h的卫星钟差数据拟合实验,观察钟差模型化结果的精度,并将得到的模型化钟差应用于精密单点定位,得出以下结论:
1) 结合周期项的混合函数模型比单纯的多项式模型更适合对钟差进行拟合,进一步证明周期性是卫星钟差特性中不可忽略的一部分。对于Rb钟卫星,Block ⅡF卫星钟差混合函数模型化精度达到0.03 m(约0.1 ns)左右,Block ⅡR和Block ⅡR-M卫星钟差混合函数模型化精度达到0.05 m(约0.2 ns)左右。
2) Cs钟卫星钟差稳定性远次于Rb钟,模型化精度只能达到dm级,证明上述模型化方法不适合Cs钟卫星。至于未来可能存在的氢钟等新型原子钟,模型化的实用性尚待进一步实验。
3) 结合周期项的混合函数模型化钟差PPP结果的精度可达cm级,收敛时间约为4 h。由此可以认为,混合函数模型得到的少量参数可以在一定时间范畴内替代IGS提供的数据序列,进而减少卫星钟差的传输数据量,简化卫星钟差服务。
| [1] |
Dow J M, Neilan R E, Rizos C. The International GNSS Service in a Changing Landscape of Global Navigation Satellite Systems[J]. Journal of Geodesy, 2009, 83(3): 191-198
(  0) 0) |
| [2] |
Allan D W. Time and Frequency(Time-Domain) Characterization, Estimation, and Prediction of Precision Clocks and Oscillators[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 1987, 34(6): 647-654 DOI:10.1109/T-UFFC.1987.26997
(  0) 0) |
| [3] |
崔先强, 焦文海. 灰色系统模型在卫星钟差预报中的应用[J]. 武汉大学学报:信息科学版, 2005, 30(5): 447-450 (Cui Xianqiang, Jiao Wenhai. Grey System Model for the Satellite Clock Error Predicting[J]. Geomatics and Information Science of Wuhan University, 2005, 30(5): 447-450)
(  0) 0) |
| [4] |
Stein S R, Evans J. The Application of Kalman Filters and ARIMA Models to the Study of Time Prediction Errors of Clocks for Use in the Defense Communication System (DCS)[C]. Symposium on Frequency Control, 1990
(  0) 0) |
| [5] |
黄观文, 张勤, 许国昌, 等. 基于频谱分析的IGS精密星历卫星钟差精度分析研究[J]. 武汉大学学报:信息科学版, 2008, 33(5): 496-499 (Huang Guanwen, Zhang Qin, Xu Guochang, et al. IGS Precise Satellite Clock Model Fitting and Its Precision by Using Spectral Analysis Model[J]. Geomatics and Information Science of Wuhan University, 2008, 33(5): 496-499)
(  0) 0) |
| [6] |
Senior K L, Ray J R, Beard R L. Characterization of Periodic Variations in the GPS Satellite Clocks[J]. GPS Solutions, 2008, 12(3): 211-225 DOI:10.1007/s10291-008-0089-9
(  0) 0) |
| [7] |
郑作亚, 党亚民, 卢秀山, 等. 附有周期项的预报模型及其在GPS卫星钟差预报中的应用研究[J]. 天文学报, 2010, 51(1): 95-102 (Zheng Zuoya, Dang Yamin, Lu Xiushan, et al. Prediction Model with Periodic Item and Its Application to the Prediction of GPS Satellite Clock Bias[J]. Acta Astronomica Sinica, 2010, 51(1): 95-102)
(  0) 0) |
| [8] |
张杰, 周渭, 宣宗强, 等. 卫星钟差预报模型中周期项的选取方法及性能分析[J]. 天文学报, 2013, 54(3): 282-290 (Zhange Jie, Zhou Wei, Xuan Zongqiang, et al. Selection of Periodic Items and Its Performance in the Forcasting Model of Satellite Clock Bias[J]. Acta Astronomica Sinica, 2013, 54(3): 282-290)
(  0) 0) |
| [9] |
Li H, Zhou X, Wu B. Fast Estimation and Analysis of the Inter-Frequency Clock Bias for Block ⅡF Satellites[J]. GPS Solutions, 2013, 17(3): 347-355 DOI:10.1007/s10291-012-0283-7
(  0) 0) |
| [10] |
孙大伟. GNSS星载原子钟性能分析理论与算法研究[D]. 西安: 长安大学, 2016 (Sun Dawei. Study of the Theory and Algorithm for GNSS Satellite Clock[D]. Xi'an: Chang'an University, 2016) http://cdmd.cnki.com.cn/Article/CDMD-10424-1017295193.htm
(  0) 0) |
| [11] |
Vannicola F, Beard R, White J, et al. GPS Block ⅡF Atomic Frequency Standard Analysis[C]. 42nd Annual Precise Time and Time Interval (PTTI) Application and Planning Meeting, 2010
(  0) 0) |
2. No. 10 Gold Party of PAP, Kunming 650111, China
 2018, Vol. 38
2018, Vol. 38

