时间同步的精度及其完好性对于编队/星座系统中各个节点协同工作至关重要。时间同步技术包括物理同步和数学同步。针对LEO编队/星座,由于成本约束无法携带高精度原子钟,GNSS技术成为时间同步重要的选择。然而,随着GNSS授时精度的提升,其要成为LEO时间同步技术的核心还存在完好性保证问题。目前的完好性算法主要针对航空和地面接收机用户[1-7],航天器用户涉及的较少。本文针对基于GNSS的LEO卫星TRAIM问题,详细推导基于GNSS的LEO卫星TRAIM可用性算法,并以GPS+BDS为例开展仿真研究,为基于星载GNSS的LEO时间同步方案的可靠性设计提供参考。
1 基于GNSS的LEO卫星TRAIM检测可用性算法 1.1 GNSS观测模型将GNSS(GPS+BDS)观测方程线性化,得:
| $ \mathit{\boldsymbol{Y = AX}} - \mathit{\boldsymbol{\varepsilon }} $ | (1) |
式中,
| $ \mathit{\boldsymbol{V = }}\left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{A}}{{\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)}^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}} \right)\mathit{\boldsymbol{\varepsilon }} $ | (2) |
则验后单位权中误差为:
| $ \hat \sigma = \sqrt {\frac{{{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{V}}}}{{l - t}}} $ | (3) |
式中,l为可观测卫星总数; t为待解未知数个数,单系统时取4,双系统时取5。
1.2 TRAIM故障检测算法为确保上述定位和授时解算精度的完好性,需进行TRAIM粗差探测。若伪距残差向量V中各向量相互独立,并服从均值为0、方差为σ02(取52)的正态分布,则VTV/σ02服从自由度为l-t的χ2分布;若V的均值不为0,则VTV/σ02服从自由度为l-t的非中心化χ2(中心化参数为λ)分布。假设:
无故障假设H0:E(ε)=0,
有故障假设H1:E(ε)≠0,
GNSS系统无伪距故障时,若出现故障告警则为误警。给定误警概率PFA(设为10-7),则:
| $ \begin{array}{*{20}{c}} {{P_r}\left( {{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{V}}/\sigma _0^2 < {T^2}} \right) = }\\ {\int_0^{{T^2}} {{f_{{\chi ^2}\left( {l - t} \right)}}\left( x \right){\rm{d}}x = 1 - {P_{{\rm{FA}}}}} } \end{array} $ | (4) |
通过式(4)可以确定检验统计量VTV/σ02的门限阈值T,则:
| $ {\sigma _T} = {\sigma _0}T/\sqrt {l - t} $ | (5) |
若
利用上述方法进行故障检测存在一个问题,当卫星几何条件不佳时,如果某颗卫星存在故障,尽管会产生较大的定位和授时误差,但
当存在故障卫星时,将检测统计量VTV/σ02与门限阈值的平方T2进行比较,若VTV/σ02 < T2,则为漏检。给定漏检概率PMD,则有:
| $ \begin{array}{*{20}{c}} {{P_r}\left( {{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{V}}/\sigma _0^2 < {T^2}} \right) = }\\ {\int_0^{{T^2}} {{f_{{\chi ^2}\left( {l - t, \lambda } \right)}}\left( x \right){\rm{d}}x = {P_{{\rm{MD}}}}} } \end{array} $ | (6) |
给定误警率PFA和漏检概率PMD,利用式(6)可以计算得到非中心化参数λ。
通过计算误差保护限值PL来保证TRAIM的误警率和漏检率需求,进而对卫星几何结构进行质量保证。传统的时间同步误差保护限值都是在一维空间下计算的[8-9],而基于GNSS的LEO时间同步,因难以获取实时的高精度轨道信息,本文将位置和钟差信息联合解算,进而计算授时误差保护限值。定义授时误差保护限值为[1]:
| $ {\rm{TPL = }}\delta {\rm{TDO}}{{\rm{P}}_{\max }} \times {\sigma _0} \times \sqrt \lambda $ | (7) |
基于上述分析,在进行TRAIM故障检测前,需要实时计算各卫星对应的δTDOP。若δTDOPmax小于精度因子限值,则表示一个故障存在于最难监测卫星的假设下,能够保证漏检概率。计算公式为:
| $ \delta {\rm{TDO}}{{\rm{P}}_{\max }} = \max \left( {\sqrt {\frac{{\mathit{\boldsymbol{A}}_{4i}^{*2}}}{{{\mathit{\boldsymbol{Q}}_{Vii}}}}} } \right)或\max \left( {\sqrt {\frac{{\mathit{\boldsymbol{A}}_{5i}^{*2}}}{{{\mathit{\boldsymbol{Q}}_{Vii}}}}} } \right) $ | (8) |
其中, A*=(ATA)-1AT, Aji*(j=4, 5)为A*的第j行,QV=(I-A(ATA)-1AT)。
将保护限值TPL与告警阈值TAL(目前授时精度需求约为100 ns)比较,可以给出故障的完好性保证,即如果TPL小于TAL,则算法可用;反之,则算法不可用。
2 基于GNSS的LEO卫星TRAIM可用性仿真分析为分析基于GNSS的LEO卫星TRAIM可用性,首先基于STK和MATLAB开发的联合仿真平台仿真GPS31+BDS35星座,其中GPS星座为2014-10的真实星座,BDS星座中GEO是2014-10的5颗GEO,另外仿真了3颗IGSO和27颗MEO星座[10]。观测值误差设为中误差为5 m的随机参数,数据采样率为1 min,卫星截止高度角为3°。主要选取BDS单系统和GPS+BDS等两种方案进行分析。选取高度分别为500 km(大规模微纳卫星等)、650 km(遥感卫星等)、800 km(铱星、海洋卫星等)和1 400 km(空间信息网络低轨星座)的极轨卫星(轨迹可覆盖全球)等4种具有代表性的轨道类型,以验证基于GNSS的LEO卫星TRAIM可用性。4颗卫星星下点轨迹分布如图 1(圆点、三角、十字、方块分别是500 km、650 km、800 km、1 400 km轨道高度的卫星星下点轨迹)。对4颗卫星2 d内的授时检测保护限值进行统计,见图 2~5。

|
图 1 4颗卫星2 d内星下点轨迹分布图(5 min采样) Fig. 1 Distribution of tracks of sub-satellite points for four satellites during two days(interval of 5 minutes) |

|
图 2 500 km卫星授时误差检测保护限值 Fig. 2 Timing protection level for the satellite with the altitude of 500 km |
|
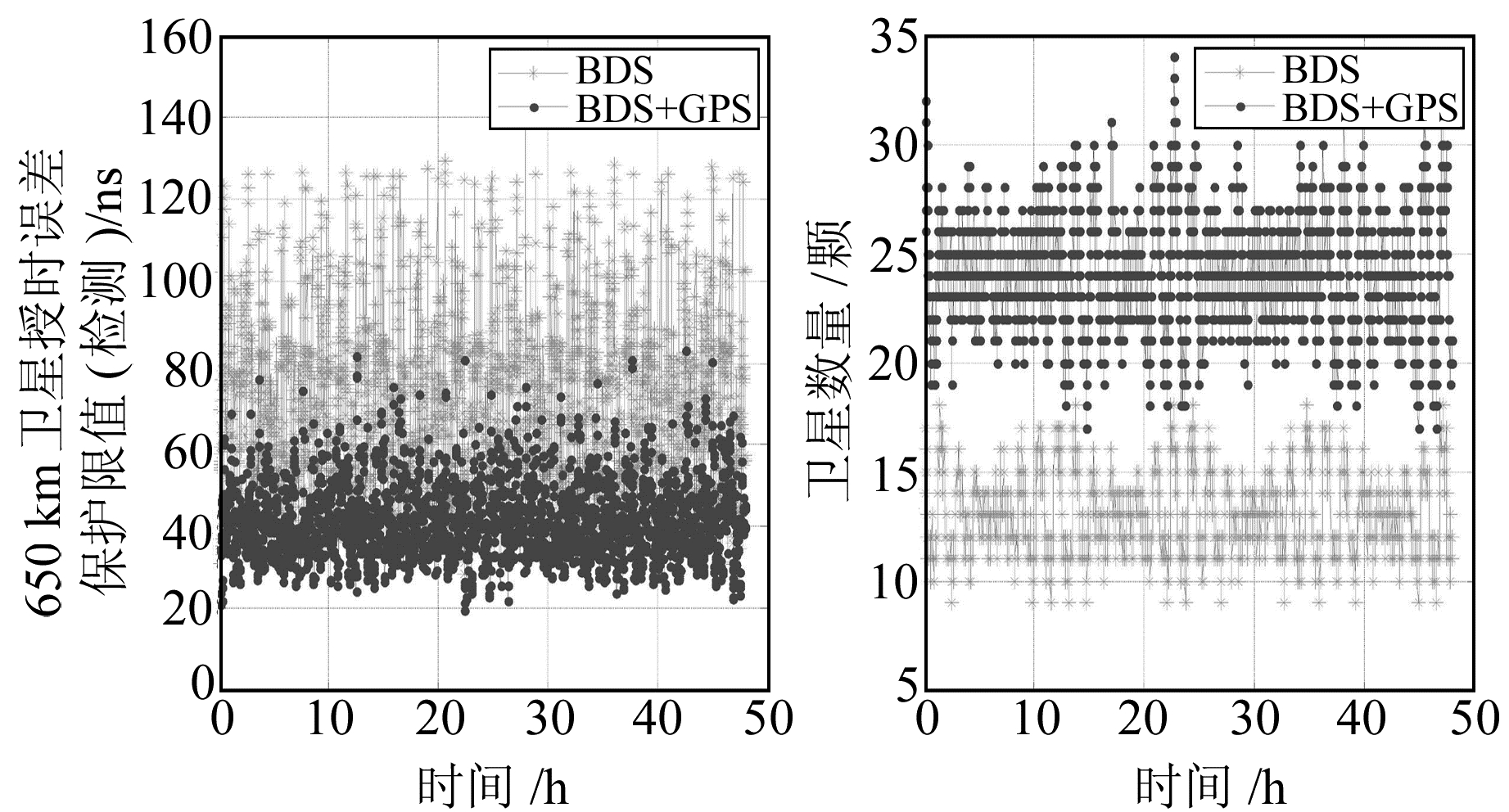
图 3 650 km卫星授时误差检测保护限值 Fig. 3 Timing protection level for the satellite with the altitude of 650 km |

|
图 4 800 km卫星授时误差检测保护限值 Fig. 4 Timing protection level for the satellite with the altitude of 800 km |
|
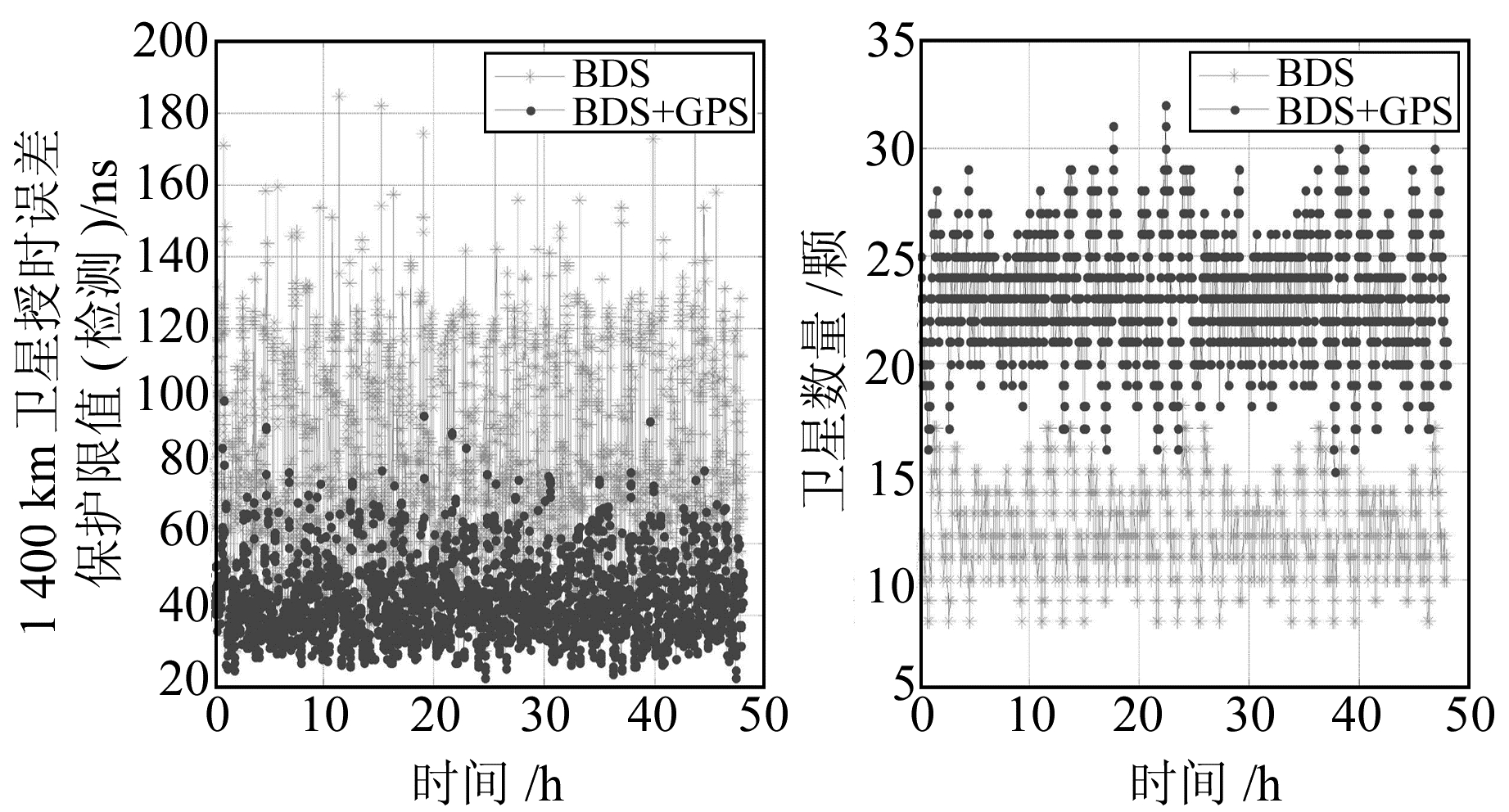
图 5 1 400 km卫星授时误差检测保护限值 Fig. 5 Timing protection level for the satellite with the altitude of 1 400 km |
可以看出,在单系统模式下,4颗卫星授时误差检测保护限值大部分位于50~140 ns;在组合系统模式下,授时误差检测保护限值基本都位于30~70 ns。将授时误差保护限值与20 ns、30 ns、40 ns、50 ns、70 ns、80 ns、100 ns等各种告警阈值进行比较,其可用性概率统计见图 6和表 1。

|
图 6 不同轨道高度不同告警阈值下LEO卫星TRAIM可用性概率统计 Fig. 6 Probability statistics of availability of TRAIM for LEOs from different altitudes with different protection levels |
|
|
表 1 不同轨道高度LEO卫星TRAIM可用性概率统计(告警阈值分别为70 ns和100 ns) Tab. 1 Probability statistics of availability of TRAIM for LEOs from different altitudes (protection levels of 70 ns and 100 ns) |
1) 随着卫星轨道高度增加,TRAIM检测可用性概率逐步降低。单系统模式下,1 400 km高度的卫星TRAIM比500 km高度的卫星TRAIM检测可用性低10%~13%。
2) 在误警率10-7和漏警率10-3概率约束下,在TRAIM告警阈值为70 ns和BDS单系统星座分布均匀时,TRAIM检测可用性对于500~800 km高度的卫星均只能实现35%左右的可用概率;而GPS+BDS组合系统TRAIM检测可用性对于500~1 400 km高度的卫星可以实现88%以上的可用概率,难以满足LEO授时完好性需求。
3) 在误警率10-7和漏警率10-3概率约束下,在TRAIM告警阈值为100 ns和BDS单系统星座分布均匀时,TRAIM检测可用性对于500~650 km高度的卫星能实现65%以上的可用概率,800 km以上为60%左右;而GPS+BDS组合系统TRAIM检测可用性,对于500~1 400 km高度的卫星均可实现99.1%以上的可用概率,基本满足LEO授时完好性需求。其中,500 km高度的卫星能够满足99.7%(3倍中误差)以上的概率。
3 结语本文详细推导了基于GNSS的LEO卫星TRAIM故障检测数学模型以及两者的可用性算法。仿真结果表明,告警阈值70 ns时,BDS单系统可以实现约50%的可用概率,而基于GPS+BDS组合系统的TRAIM检测可用概率达到88%以上;告警阈值100 ns时,BDS单系统可以实现60%~70%的检测概率,而基于GPS+BDS组合系统的TRAIM检测可用概率达到99.1%。整体来讲,基于GPS+BDS组合时间同步方案能够满足LEO卫星TRAIM可用性需求,即能保证单星故障可检测的可用性,对于时间同步精度完好性至关重要。此方案对于LEO实时时间同步很有发展前景。后续将考虑LEO卫星轨道预报信息进行约束,增强时间同步RAIM可用性,为工程化实施和应用提供参考。
| [1] |
陈金平, 许其凤, 刘广军. GPS RAIM水平定位误差保护限值算法分析[J]. 测绘学院学报, 2001, 18(S1): 1-3 (Chen Jinping, Xu Qifeng, Liu Guangjun. Analysis of Different Algorithms for GPS RAIM HPL[J]. Journal of Institute of Surveying and Mapping, 2001, 18(S1): 1-3)
(  0) 0) |
| [2] |
蒋虎, 袁运斌, 王海涛, 等. 精密进近阶段的多系统GNSS组合RAIM可用性算法及分析[J]. 中国空间科学技术, 2016, 36(3): 32-40 (Jiang Hu, Yuan Yunbin, Wang Haitao, et al. Multi-GNSS RAIM Availability Algorithms and Analysis for Precise Approach[J]. Chinese Space Science and Technology, 2016, 36(3): 32-40)
(  0) 0) |
| [3] |
Ober P B, Harriman D. On the Use of Multiconstellation-RAIM for Aircraft Approaches[C]. ION GNSS, Fort Worth, 2006
(  0) 0) |
| [4] |
Ene A. Further Development of Galileo-GPS RAIM for Vertical Guidance[C]. ION GNSS, Fort Worth, 2006
(  0) 0) |
| [5] |
Ene A, Blanch J, Walter T. Galileo-GPS RAIM for Vertical Guidance[C]. ION NTM, Monterey, 2006
(  0) 0) |
| [6] |
Martineau A, Macabiau C, Mabilleau M. GNSS RAIM Assumptions for Vertically Guided Approaches[C]. 22nd International Technical Meeting of the Satellite Division of the Institute of Navigation, Savannah, 2009
(  0) 0) |
| [7] |
陈坡, 孙付平, 景晓鹏, 等. 基于惯导辅助的GNSS完好性检测方法研究[J]. 大地测量与地球动力学, 2013, 33(2): 102-104 (Chen Po, Sun Fuping, Jing Xiaopeng, et al. Integrity Monitoring Technique of GNSS Based on INS[J]. Journal of Geodesy and Geodynamics, 2013, 33(2): 102-104)
(  0) 0) |
| [8] |
Geier G J, King T M, Kennedy H L, et al. Prediction of the Time Accuracy and Integrity of GPS Timing[C]. IEEE International, 1995
(  0) 0) |
| [9] |
王爱兵, 何海波, 郭睿, 等. GPS测时的接收机自主完好性监测算法[J]. 海洋测绘, 2007, 27(3): 28-30 (Wang Aibing, He Haibo, Guo Rui, et al. The Algorithm of GPS Timing Receiver Autonomous Integrity Monitoring[J]. Hydrographic Surveying and Charting, 2007, 27(3): 28-30)
(  0) 0) |
| [10] |
中国卫星导航系统管理办公室. 北斗卫星导航系统公开服务性能规范(1. 0版)[Z]. 北京, 2013 (China Satellite Navigation System Management Office. The Public Service Performance Specification for Beidou Satellite Navigation System(Version 1. 0)[Z]. Beijing, 2013)
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38

