GPS软件接收机具有成本低、扩展性强和灵活性高等优势，已逐步替代传统的GPS硬件接收机。信号捕获和跟踪是GPS软件接收机的核心，也是目前研究的热点^[1-3]。对特定GPS卫星而言，GPS信号捕获就是对C/A码相位和频率的二维搜索，称为C/A码捕获^[4]。C/A码捕获包括串行和并行两种方式。串行方式因其时间消耗大，已较少采用。基于C/A码的周期性，采用FFT并行计算可以实现高速信号捕获^[5]，但FFT只解决了捕获的速度问题，却不能对微弱GPS信号进行捕获^[6-8]。文献[9]提出基于分段移位平均周期图的高动态GPS信号捕获算法，实现低信噪比下大动态范围的GPS信号捕获，但算法复杂度较高；文献[10]提出一种部分匹配滤波与FFT粗捕获和线性调频Z变换精捕获方法，实现了高动态信号捕获，但信噪比低时捕获性能不佳；文献[11]设计了一种并行频域搜索捕获算法，可在同一时间对所有码时延进行处理，减少运算量，但其对弱信号的捕获能力有待提高。

针对弱信号条件下的GPS信号捕获问题，本文采用平均相关处理提高对微弱信号的捕获能力，基于叠加相关提高信号捕获过程中大量相关运算的计算效率，通过频偏校正和内插为后续信号跟踪提供精度较高的频率估计结果。相比已有捕获方法，该方法能够对信噪比较低的GPS信号进行精度较高的快速捕获，为GPS软件接收机信号捕获提供一种新的思路。

1 C/A捕获问题

进入GPS软件接收机的卫星信号经RF前端混频和AD采样处理后，数字基带信号为：

$ \begin{array}{*{20}{c}} {x({t_n}) = {\text{A}}{{\text{D}}_k}({t_n}){C_k}\left[ {\left( {1 + \eta } \right)({t_n} - {t_\tau })} \right]} \\ {{\text{cos}}\left[ {({\omega _{{\text{IF}}}} - {\omega _D}){t_n} + {\varphi _0}} \right] + v({t_n})} \end{array} $

(1)

式中，A表示信号幅度，为常数；t_n表示采样后的时间序列；D_k(t_n)表示GPS导航电文数据序列，间隔20 ms在±1中随机取值；C_k(t_n)代表卫星的伪随机编码，也就是要捕获的C/A码；t_τ代表C/A码的起始码相位；η代表信号多普勒频偏C/A码相位的影响因子；ω_IF为混频后输出的中频频率；ω_D为GPS接收机与卫星之间相对运动产生的多普勒频偏；φ₀代表初始相位；v(t_n)代表加性高斯白噪声。如果忽略电离层的影响，影响因子与多普勒频偏之间存在以下关系：

$ \eta = \frac{{{\omega _D}}}{{2{\rm{ \mathsf{ π} }} \times 1575.42 \times {{10}^6}}} $

(2)

要捕获第k颗卫星信号，首先要在软件接收机中复制出该卫星C/A码中频信号的同向分量和正交分量：

$ I({t_n}) = {C_k}\left[ {\left( {1 + \hat \eta } \right)({t_n} - {t_{\hat \tau }})} \right]{\rm{cos}}\left[ {({\omega _{{\rm{IF}}}} - {{\hat \omega }_D}){t_n}} \right] $

(3)

$ Q({t_n}) = - {C_k}\left[ {\left( {1 + \hat \eta } \right)({t_n} - {t_{\hat \tau }})} \right]{\rm{sin}}\left[ {({\omega _{{\rm{IF}}}} - {{\hat \omega }_D}){t_n}} \right] $

(4)

式中，${C_k}\left[ {\left( {1 + \hat \eta } \right)({t_n} - {t_{\hat \tau }})} \right]$表示本地复制的C/A码，${\rm{cos}}\left[ {({\omega _{{\rm{IF}}}} - {{\hat \omega }_D}){t_n}} \right]$和${\rm{sin}}\left[ {({\omega _{{\rm{IF}}}} - {{\hat \omega }_D}){t_n}} \right]$分别表示本地复制的同向载波和正交载波，${\hat \eta }$、${{t_{\hat \tau }}}$和${{{\hat \omega }_D}}$分别表示η、t_τ和ω_D的估计值。由于η和ω_D存在耦合关系，因此C/A码捕获问题就是一个关于${{t_{\hat \tau }}}$和${{{\hat \omega }_D}}$的二维搜索问题。

将本地复制信号与GPS信号进行相关运算后组成复信号，忽略影响因子η，化简为：

$ \begin{array}{*{20}{c}} {z({t_n}) = 0.5A{D_k}({t_n})R(\Delta {t_\tau }) \cdot }\\ {\sin c\left[ {\Delta {\omega _d}{t_n}} \right]{{\rm{e}}^{ - {\rm{j}}\left[ {\Delta {\omega _d}{t_n} + \varphi } \right]}} + w({t_n})} \end{array} $

(5)

式中，R(·)为C/A的自相关函数；$\Delta {t_\tau } = \left| {{t_\tau } - {t_{\hat \tau }}} \right|$为本地复制C/A码与接收机C/A码的码相位偏差；sinc(·)为辛格函数；$\Delta {\omega _d} = \left| {{\omega _d} - {{\hat \omega }_d}} \right|$为本地复制信号与接收机信号多普勒频率之间的频率差；w(t_n)代表相关运算后的噪声。当${t_{\hat \tau }} = {t_\tau }$且${{\hat \omega }_d} = {\omega _d}$时，信号相关z(t_n)取得最大值。因此，遍历t_τ和ω_d，将z(t_n)最大值与门限比较即可实现C/A码的捕获，同时完成码相位和多普勒频偏的粗估计。

为减小运算复杂度，可以基于FFT并行实现C/A码快速捕获^[6]。接收信号与本地复制信号之间的自相关表示为：

$ \begin{array}{*{20}{c}} {z({t_m}) = \sum\limits_{{t_n} = 0}^{N - 1} {x({t_n} + {t_m})C({t_n}) = } {\rm{ }}}\\ {{\rm{FFT}}\left[ {X\left( k \right){C^*}\left( k \right)} \right]} \end{array} $

(6)

2 算法原理 2.1 平均相关处理

由C/A信号捕获过程可知，自相关损耗是影响微弱信号C/A捕获的关键。由C/A码自相关函数可知，采样间隔越小，自相关损耗就越小，越有利于捕获微弱信号。但是，采样间隔的降低会显著提高捕获算法的运算复杂度，降低C/A信号捕获的时效性。因此，本文提出一种基于平均相关的微弱信号捕获方法。

平均相关的思路是对经过高速采样的GPS信号和本地复制信号均进行分组，对分组后信号进行并行相关运算。首先按每组信号M个采样点数对接收到的GPS信号进行分组，然后将各组内的第一个采样组合构成一个新的信号片段，从而生成M个信号片段。本次复制信号进行同样的分组，经过相关并行运算后，就会获得M组相关结果，累加后即可实现信号捕获。

不失一般性，假设C/A码为矩形码片，码片宽度为T_c。当采样间隔小于等于码片宽度，即|Δt_τ≤T_c|时，C/A码的自相关函数为：

$ R\left( {\Delta {t_\tau }} \right) = {A^2}\left( {1 - \frac{{\Delta {t_\tau }}}{{{T_c}}}} \right) $

(7)

传统相关捕获算法的码搜索步长通常设为码片宽度的一半，而高采样速度的平均相关捕获可以设置很小的搜索步长。例如传统相关捕获的步长为T_c/2，平均相关捕获则可以获得T_c/32的步长。代入式(7)可得出，平均相关捕获能够改善2 dB以上的自相关损耗。

GPS接收信号中存在多普勒频偏，需要本地复制信号进行频点步进搜索。搜索步长也会影响自相关函数的损耗：

$ \sin c\left( {\Delta {\omega _d}{t_n}} \right) = \frac{{\sin \left( {\Delta {\omega _d}{t_n}} \right)}}{{\Delta {\omega _d}{t_n}}} $

(8)

式(8)表明，要想获取较小的自相关函数峰值，搜索步长就要相应减小，但步长减小会影响到计算效率，实际应用时要综合考虑。

2.2 叠加相关处理

在C/A码捕获过程中，都是通过累积来提高捕获灵敏度，其实质就是信号相关。因此，C/A码捕获需要大量的相关运算(平均分组后大量运算仍然是相关运算)。为了提升捕获速度，本文采用先叠加后相关的思想降低相关运算复杂度。

假设x_p(t_n)是经过平均分组后的某组GPS信号，信号时长1 ms，y(t_n)为本地复制C/A码信号，则需要完成的相关运算为：

$ Z\left( k \right) = {X_p}\left( k \right)Y\left( k \right) $

(9)

式中，X_p(k)、Y(k)为x_p(t_n)、y(t_n)的FFT。

设信号的相关累积长度为P ms，则共需要进行P次相关累加：

$ {Z_\Delta }\left( k \right) = \sum\limits_{p = 1}^P {{X_p}\left( k \right)Y\left( k \right) = } Y\left( k \right){\rm{FFT}}\left[ {\sum\limits_{p = 1}^P {{x_p}\left( {{t_n}} \right)} } \right] $

(10)

式(10)表明，只需一次相关运算和少量累加运算就可以取得多次相关运算所能取得的结果，显著降低了相关累加的计算复杂度。

此外，为了能够利用FFT并行快速算法，需要C/A码周期采样点数符合2ⁿ的要求。但是，如果采用直接补零的方式将采样点数凑齐2ⁿ，就会严重破坏C/A码的相关性，FFT并行运算后，自相关峰值会出现分裂，影响捕获性能。本文采用文献[12]提出的线性插值方式，将C/A码周期采样点数凑齐2ⁿ。通过线性插值，既满足FFT并行运算的要求，又不会影响自相关峰值。需要注意的是，线性插值会改变采样频率，因此要满足带通采样定理的要求。

2.3 频偏校正和内插

根据C/A码捕获过程，多普勒频偏会降低自相关函数峰值，因此需要进行频偏补偿。对于每一个本地复制信号的搜索频点，首先计算对应的多普勒频偏${{\hat \omega }_D}$，然后按照式(2)中多普勒频偏与影响因子的关系进行补偿线性插值，校正多普勒频偏对自相关函数峰值的影响。

C/A码捕获过程中，为降低捕获时间，通常会采用较大的频率搜索步长，频率分辨率较低。FFT并行运算后，自相关峰值对应的频点与实际频点存在较大差距。为了给后续GPS信号跟踪提供精确的频率信息，以自相关峰值对应频点为基础进行新一轮频点搜索，严重影响捕获效率。为此，本文借助正弦波信号频率估计中的Rife插值思想，采用内插方式获取精确的频点信息。

经过FFT并行运算后，自相关函数峰值记为Z_m，Z_m对应频点记为ω_m0，与Z_m相邻的左右两个频点的自相关值记为Z_m-1、Z_m+1，则C/A码捕获频点估计值为：

$ {\omega _0} = \left( {{\omega _{m0}} + r\frac{{\left| {{Z_{m + r}}} \right|}}{{\left| {{Z_m}} \right| + \left| {{Z_{m + r}}} \right|}}} \right) \cdot \Delta f $

(11)

式中，Δf为FFT并行运算的频率分辨率，当A_k0+1 < A_k0-1时，r=-1；当A_k0+1≥A_k0-1时，r=1。经过内插后，可以获得较高的频率估计精度，避免二次搜索，显著降低捕获时间。

3 算法实现

为了实现微弱GPS信号的捕获，必须对多段相关结果累积，进一步提升信号处理增益。累积方法包括相干累积、非相干累积和差分相干累积。相干累积能够有效消除噪声，提高捕获灵敏度，最大限度地提高处理增益，但由于GPS信号的特殊性(导航电文数据存在相位跳变)，导致相关累积时间不能过长。非相干累积可以进行长时间累积，但是一种非线性预运算，对微弱信号的捕获性能不佳。差分相干累积是将当前周期相关值与前一周期相关值共轭相乘后再进行累积，对导航电文数据跳变不敏感，但相邻的相关数据会存在一定差异，对微弱GPS信号的捕获性能欠佳。

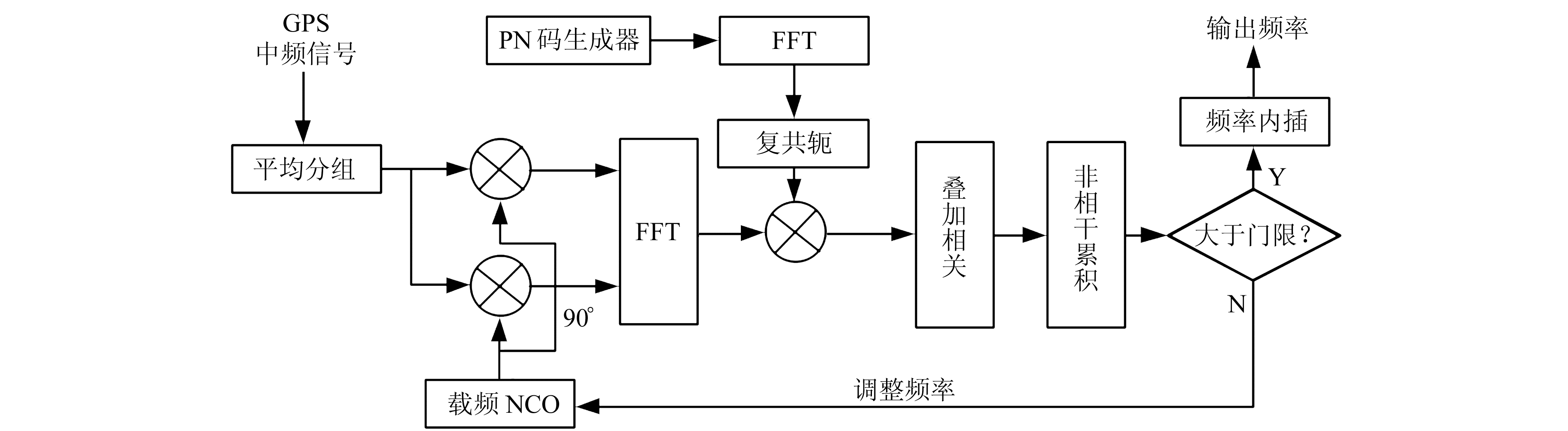
本文采用相干非相干累积方法，首先进行一段相干累积，然后对相干累积结果进行非相干累积，如图 1所示。

4 实验与分析

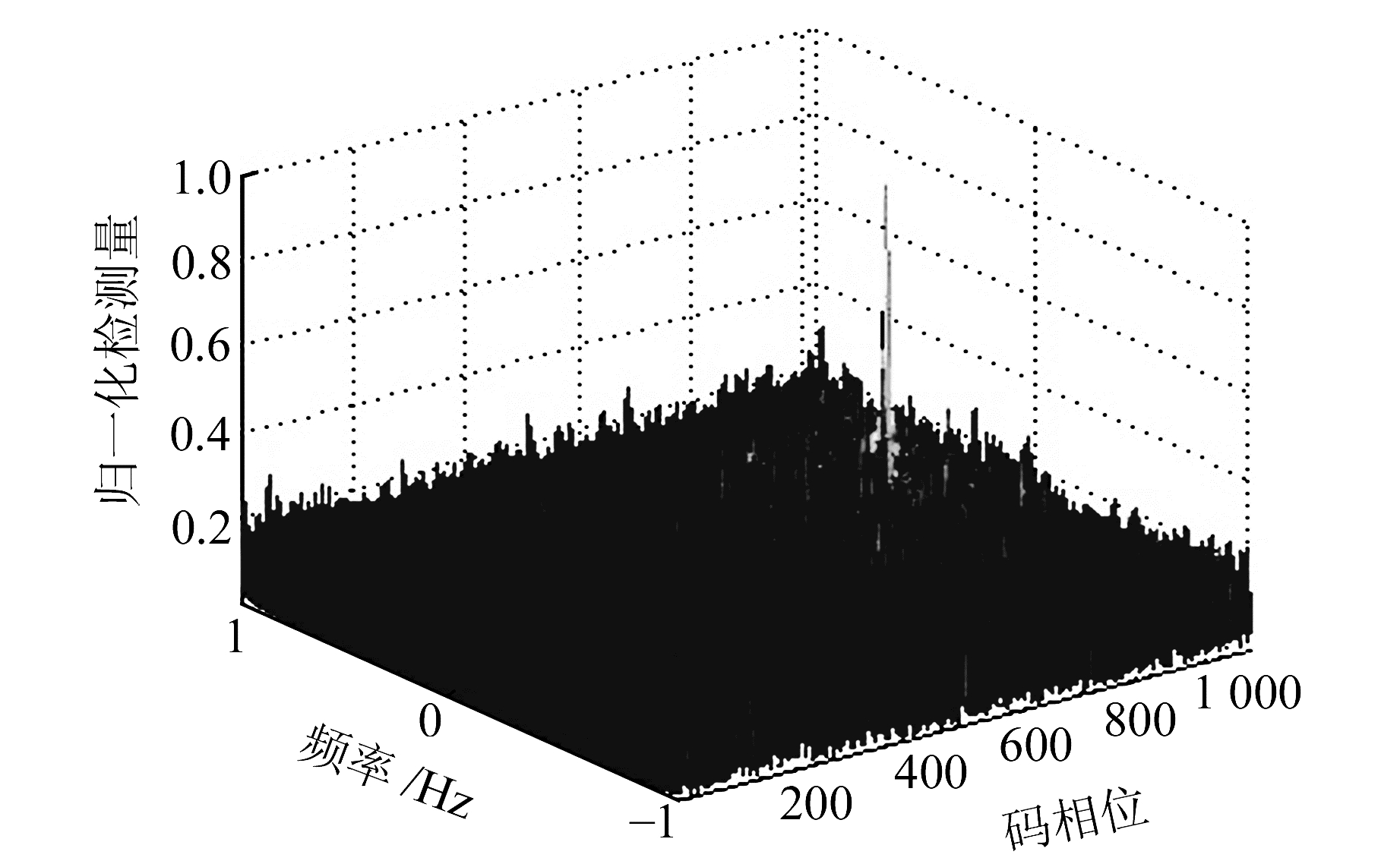
利用SiGe半导体公司的SE4120L射频前端，混频后输出的信号频率为4.092 MHz，采样频率为16.368 MHz，将实际采集数据导入计算机。捕获过程中，码相位搜索步长T_c/64，相干累积12次，基于Matlab进行算法的捕获测试。图 2为利用本文算法对2017-10-18 13:00左右10号GPS卫星的捕获结果。

实测表明，本文提出的基于平均分组和叠加相关的捕获方法能够有效捕获实际GPS信号，验证了算法的有效性。在同一台计算机中，对本文算法和传统FFT并行捕获算法^[7]的时间消耗进行对比，频域并行捕获算法的码相位搜索步长均设为T_c/64，且采用相同的相干非相干累积方法，结果见表 1。结果表明，本文算法的时间消耗远远小于传统的FFT并行捕获算法。传统的FFT并行算法难以捕获微弱信号的原因主要是受计算效率限制，难以进行精细码相位搜索。本文采用平均分组结合叠加相关，较好地解决了这个矛盾，既能够实现精细搜索，又保证了时间消耗。

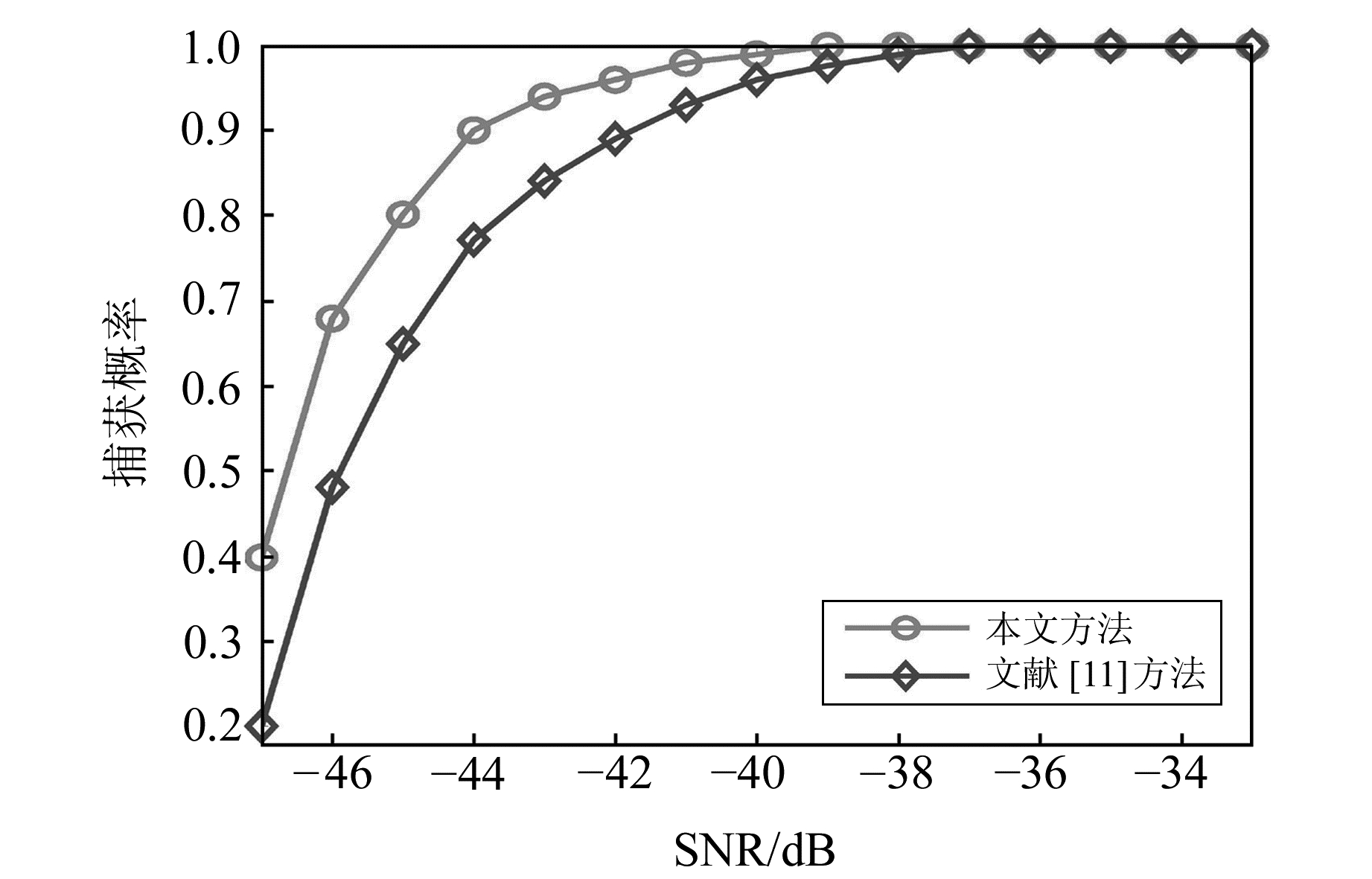
实际采集的GPS信号无法控制信噪比，难以有效评价捕获算法对微弱GPS信号的捕获能力。为此，利用计算机仿真产生不同信噪比的GPS信号。仿真生成8号GPS卫星信号，信号频率为4.092 MHz，采样频率为16.368 MHz，数据长度200 ms，导航电文数据随机取值，信号中混入加性零均值高斯白噪声。通常，高灵敏度GPS软件接收机要求能够捕获的微弱信号强度范围为[-174 dBW, -188 dBW]，转换为信噪比约为[-33 dB, -47 dB]。文献[11]设计一种基于并行FFT的GPS信号捕获方法，采用空间搜索替代时间搜索，能够实现GPS信号的快速捕获。分别采用本文方法和文献[11]提出的算法对不同强度的信号进行捕获测试。两种方法对不同信噪比GPS信号的捕获测试结果如图 3所示。可以看出，随着信噪比的增加，两种算法正确捕获的概率均逐渐增加，但本文算法在各个信噪比下的捕获性能均优于文献[11]算法；文献[11]算法要达到90%的正确捕获概率，要求信噪比为-41 dB以上，而本文算法只需信噪比达到-44 dB。

5 结语

本文提出一种基于平均分组和叠加相关的GPS信号捕获方法，有效调和码相位精细搜索和捕获时间消耗之间的矛盾，适用于对微弱GPS信号进行捕获。算法采用平均分组降低相关函数损耗，利用叠加相关提升运算效率，并基于频偏校正和内插提高频率捕获精度。仿真实验和实测实验表明，该方法能够有效捕获微弱GPS信号，且计算效率较高，适合于GPS软件接收机使用。