滑坡稳定性及变形研究一直是热点问题[1]。在滑坡稳定性方面,朱雷等[2]结合试验参数及数值模拟,对滑坡稳定性进行动态计算;胡安龙等[3]利用支持向量机及优化算法,构建滑坡稳定性预测模型;张夏冉等[4]根据库区水文资料分析不同渗透条件及库水位下的滑坡稳定性,得出两参数与稳定性之间的演化规律。在滑坡变形预测方面,李蔚等[5]利用双重BP神经网络模型对滑坡变形进行预测;黄海峰等[6]利用SPA模型对滑坡变形进行趋势项、周期项分解,再采用支持向量机进行预测。上述研究多是针对滑坡稳定性或变形预测方面的单一研究,缺少两者的组合。尖点突变理论用于分析事物从连续逐渐变化至破坏性突然变化的过程,对滑坡稳定性研究具有较好的适用性[7-8];非趋势波动分析(DFA)是一种广泛应用于水文领域的趋势分析方法[9-10],能对评价序列的趋势性作出有效评价。因此,本文利用尖点突变理论及非趋势波动分析对滑坡稳定性及变形趋势进行研究,探讨两种方法对滑坡稳定性及变形趋势判断的适用性。
1 基本原理 1.1 尖点突变理论突变理论将事物划分为稳定态和非稳定态,两种状态在扰动达到一定程度后可以相互转化。状态间的转化以突变形式发生。
在滑坡突变模型构建中,首先拟合得到滑坡位移变形的4次拟合函数:
| $ {Y_t} = {a_0} + {a_1}t + {a_2}{t^2} + {a_3}{t^3} + {a_4}{t^4} $ | (1) |
式中,Yt为第t时刻的变形值,a0、a1、a2、a3、a4为待拟合参数。通过Tschirhaus变换[7-8]将上式转化为尖点突变理论的标准形式。令t=x-A,A=a3/4a4,代入式(1)得:
| $ u = {b_4}{x^4} + {b_2}{x^2} + {b_1}x + {b_0} $ | (2) |
其中,参数a、b间的关系为:
| $ \left[ \begin{array}{l} {b_0}\\ {b_1}\\ {b_2}\\ {b_4} \end{array} \right] = \left[ {\begin{array}{*{20}{c}} {{A^4}}&{ - {A^3}}&{{A^2}}&{ - A}&1\\ { - 4{A^4}}&{3{A^2}}&{ - 2A}&1&0\\ {6{A^2}}&{ - 3A}&1&0&0\\ 1&0&0&0&0 \end{array}} \right]\left[ \begin{array}{l} {a_4}\\ {a_3}\\ {a_2}\\ {a_1}\\ {a_0} \end{array} \right] $ | (3) |
对式(2)进行消b4处理,得到滑坡尖点突变模型的标准形式:
| $ u = {x^4} + \mu {x^2} + vx + c $ | (4) |
式中,c为待求常数,
| $ \Delta = 8{\mu ^3} + 27{\nu ^2} $ | (5) |
当Δ>0时,滑坡处于稳定状态;当Δ < 0时,滑坡处于失稳状态;当Δ=0时,滑坡处于临界平衡状态。Δ值的大小可描述演化状态与临界状态的接近程度,且Δ>0时,其值越小稳定性越好[11]。
1.2 DFA分析非趋势波动分析是一种标度指数计算方法[12]。其分析步骤如下。
1) 累积离差计算。滑坡变形分析序列为{xt, t=1, 2, …, N},则第i个节点的累积离差为:
| $ Y\left( i \right) = \sum\limits_{k = 1}^i {\left( {{x_k} - x'} \right)} $ | (6) |
式中,x′为分析序列的均值。
2) 序列重构。将Y(i)按等长度S划分若干区间,则区间个数Ns=N/S。若序列长度N不是S的整数倍,在Ns取整数时序列后部分的相关节点将不能发挥作用。再逆序进行相同区间长度S的划分,即在区间长度S条件下,共计有2Ns个子区间。
3) 局部趋势求解。对各子区间进行最小二乘多项式拟合,选择其中最优结果,得到第i节点处的局部趋势Pv(i),进而求得滤去局部趋势的值:
| $ {Y_s}\left( i \right) = Y\left( i \right) - {P_v}\left( i \right) $ | (7) |
4) 方差求解。求解各子序列的方差:
| $ \left\{ \begin{array}{l} {F^2}\left( {\nu , s} \right) = {\rm{ }}\frac{1}{s}\sum\limits_{i = 1}^s {{{\{ Y\left[ {\left( {\nu - 1} \right)s + i} \right] - {P_\nu }\left( i \right)\} }^2}} \\ \;\;\;\;\;\;\left( {\nu = 1, 2, \ldots , 2n} \right)\\ {F^2}\left( {\nu , s} \right) = {\rm{ }}\frac{1}{s}\sum\limits_{i = 1}^s {{{\{ Y\left[ {N - \left( {\nu - n} \right)s + i} \right] - {P_\nu }\left( i \right)\} }^2}} \\ \;\;\;\;\;\;\left( {\nu = n + 1, n + 2, \ldots , 2n} \right) \end{array} \right. $ | (8) |
5) 求解波动函数。对各子序列区间的方差值求均值,并将标准DFA的波动函数表示为:
| $ F\left( S \right) = \sqrt {\frac{1}{{2{N_s}}}\sum\limits_{i = 1}^{2{N_s}} {{F^2}\left( {\nu , s} \right)} } $ | (9) |
6) 求解标度指数α。将子区间长度由2到N重复1)~5),即可得到若干散点(F(S),S),且两者之间呈幂相关。对各点进行对数处理,并将双对数坐标进行最小二乘直线拟合,得到的直线斜率即为标度指数α。
① 当0<α<0.5时,分析序列呈反相关趋势,即其下一阶段的发展趋势与前一阶段相反,且其值越小,趋势性越强。
② 当0.5<α<1时,分析序列呈正相关趋势,即其下一阶段的发展趋势与前一阶段相同,且其值越大,趋势性越强。
③ 当α=0.5时,分析序列不具有趋势性,不能对后期的发展趋势进行判断。
引入关联维数D用以评价序列节点间的关联性,其值越大说明分析序列各节点间的关联性越大。计算公式为:
| $ D = 2 - \alpha $ | (10) |
1) 通过Matlab实现滑坡位移变形的4次多项式拟合,进而求解突变参数和突变特征值。
2) 通过DFA分析求解滑坡变形的标度指数α和关联维数D,判断滑坡变形序列的趋势性和关联性。
3) 结合文献[13],得出滑坡位移变形趋势或稳定性具有的阶段性特征。在阶段性分析中,对各阶段均进行尖点突变分析和DFA分析,以对比各阶段的稳定性和变形趋势。
2 实例分析 2.1 工程概况滑坡位于三峡库区近坝段右岸,长约350 m,宽350~500 m,平均厚度约30 m,体积约400万m3。滑坡变形始于1982年,由葛洲坝水库蓄水引起,共诱发4条裂缝,裂缝走向近似平行于河流,延伸长度在60~80 m,且在1983年、1987年均出现不同程度的变形。对滑坡变形进行监测,其中中部一个监测点[14]的累计变形曲线如图 1,监测时间是2003~2010年,共监测88个周期。

|
图 1 滑坡累计变形时间曲线 Fig. 1 Accumulative deformation time curve of landslide |
由图 1看出,滑坡变形有持续增长趋势,无明显突变。对其变形速率和特征参数进行统计,如图 2和表 1。滑坡变形速率整体具有明显波动特征,但在第70周期前波动幅度均相对较小,而后期波动幅度相对较大。加之最大速率达4.370 mm/d,变形速率的极差和标准差分别为4.600 mm/d和0.600 mm/d,也说明滑坡变形速率波动较大,这主要是受季节性降雨及水库蓄水位变化的影响。同时,滑坡最小变形速率为负值,这与滑坡土体失水引起土体收缩相关,且平均值为0.359 mm/d,但总变形已达764.300 mm,说明滑坡变形具有累计变形破坏的特征。
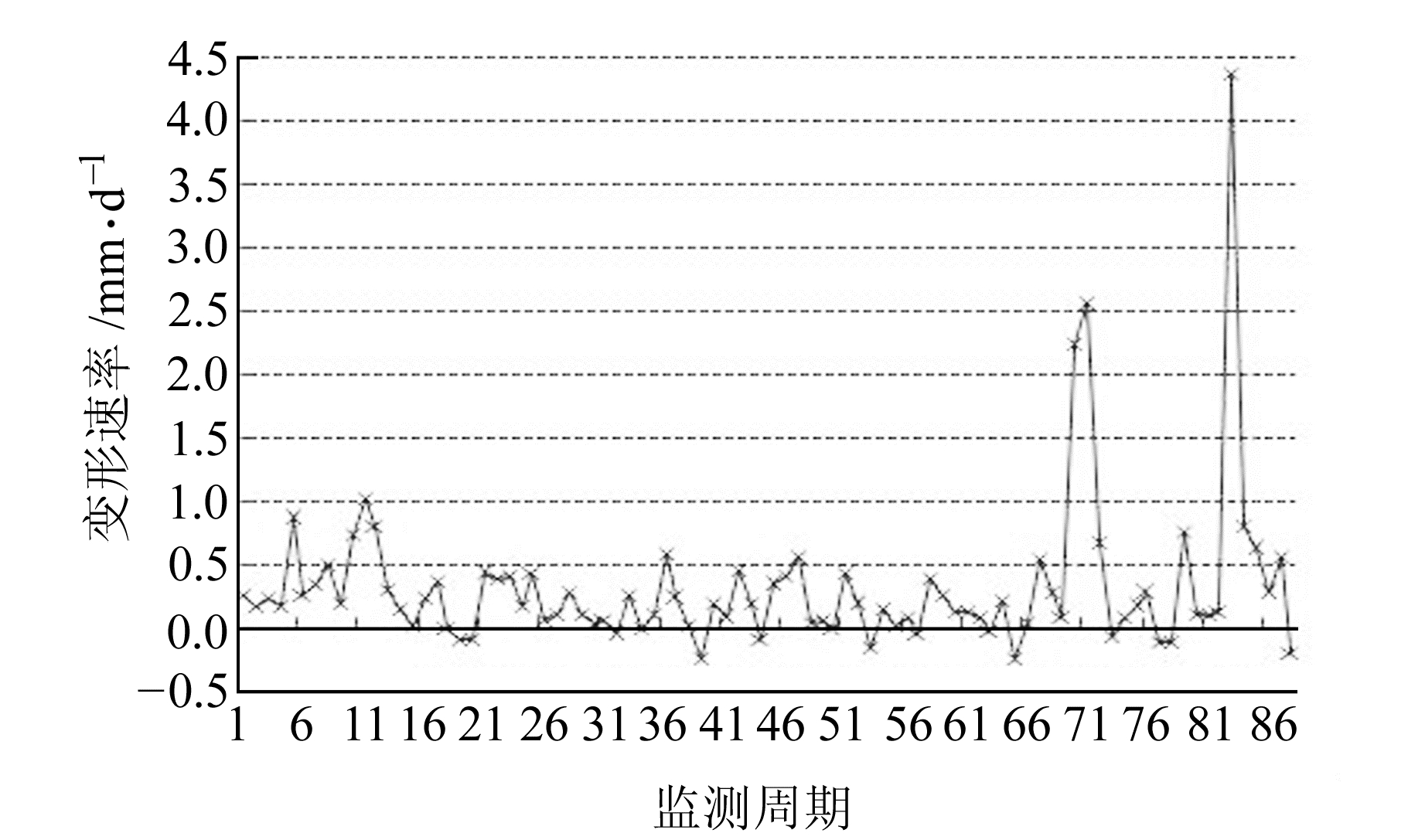
|
图 2 滑坡变形速率时间曲线 Fig. 2 Time curve of landslide deformation rate |
|
|
表 1 滑坡变形特征参数统计 Tab. 1 Statistical data of landslide deformation characteristics |
1) 整体稳定性分析
基于尖点突变理论和所有样本,对滑坡变形的整体突变参数和突变特征值进行求解。滑坡所有样本的4次拟合函数为:
| $ \begin{array}{*{20}{c}} {y = - 5.150 \times {{10}^{ - 12}}{t^4} + 1.196 \times {{10}^{ - 7}}{t^3} - }\\ {3.856 \times {{10}^{ - 4}}{t^2} + 0.589t - 32.8} \end{array} $ |
该拟合曲线的拟合精度为0.986 8,拟合效果较好。对相应特征参数求解如下:
| $ {\mu _{总}} = - 1.274 \times {10^8}, \;{\nu _{总}} = - 8.106 \times {10^{11}} $ |
则Δ总=1.209×1024>0, 滑坡处于稳定状态。
2) 分时段稳定性分析
分时段包含等时段和递增时段两种方式,其中等时段是将分析样本等分为若干时段,各时段具有相同的样本数;而递增时段是以前若干样本先进行分析,而后依次递增相应样本数进行再分析,直至分析完所有样本为止。
① 时段分析。在等时段分析中,将分析样本等分为4个阶段,每个阶段22个周期,各阶段的尖点突变分析结果统计如表 2。在等时段分析中,各阶段的突变特征值均大于0,说明各阶段的滑坡均处于稳定状态,但各阶段的突变特征值不同,说明各阶段的滑坡稳定程度各有差异;同时,各阶段的拟合度均较为趋近于1,均方根误差也较小,且变化差异不大,说明各阶段的拟合效果均较好,突变分析结果的可信度较高。
|
|
表 2 等时段的尖点突变分析结果统计 Tab. 2 Statistical analysis of cusp catastrophe at equal intervals |
② 递增时段分析。类似等时段分析,将分析样本也划分为4个阶段,第一阶段为22个周期,后续依次每次增加22个周期,分析结果统计如表 3。在递增时段分析中,各阶段的突变特征值均大于0,说明各阶段的滑坡也处于稳定状态。随监测周期的递增,突变特征值不断增加,说明滑坡的稳定性在不断减小,这与滑坡变形呈渐进性增加的特征相符。另外,各阶段的拟合度也均较为趋近于1,均方根误差也较小,各阶段拟合效果均较好。
|
|
表 3 递增时段的尖点突变分析结果统计 Tab. 3 Statistical analysis of cusp catastrophe in increasing period |
1) 整体变形趋势分析
对88个监测周期的所有样本进行DFA分析,结果如表 4所示。在滑坡整体变形趋势分析中,两序列的标度指数α均大于0.5,得出两序列将呈持续增长趋势,且累计序列偏离0.5的程度相对更大,说明累计序列较速率序列具有相对更强的趋势性。同时,速率序列的关联维数要大于累计序列,说明速率序列节点间的关联性要大于累计序列。最后,两序列的拟合度和误差平方和(SSE)均较优,说明两序列的拟合效果较优,后期DFA分析参数的可信度较高。
|
|
表 4 整体变形趋势分析 Tab. 4 Overall deformation trend analysis |
2) 分阶段变形趋势分析
为实现与尖点突变分析结果间的对比,也采取等时段和递增时段两种分阶段方式,且各阶段的区间划分均保持不变。
① 等时段趋势分析。对各等时段均进行DFA分析,结果如表 5所示。两序列在各阶段的标度指数α均大于0.5且相互不等,具有一定的变化差异,说明各阶段的变形均呈持续增长趋势,但各阶段的增长程度具有一定的差异,这与滑坡变形时间曲线的特征相符。在关联维数D方面,各阶段的速率序列较累计序列具有相对更大的关联维数,说明各阶段的速率序列节点间的关联性相对更大。最后,两序列在各阶段的拟合度和误差平方和(SSE)均较优,拟合效果较好,拟合结果较为可靠。
|
|
表 5 等时段的DFA分析结果统计 Tab. 5 Statistics of DFA analysis at equal intervals |
② 递增时段趋势分析。对各递增时段均进行DFA分析,结果如表 6所示。在递增时段的趋势分析中,各序列的标度指数α均大于0.5,说明各阶段的变形趋势呈持续增长趋势,与等时段分析结果一致。且随监测样本的累积,各序列的标度指数α值也具有一定的差异,第1阶段、第4阶段的标度指数α值相对更大,中间两阶段的标度指数α值相对较小。在关联维数D、拟合度和误差平方和(SSE)方面,与等时段分析结果一致,即速率序列具有相对更大的关联维数,其节点间的关联性相对更大,且各阶段的拟合效果也较好,拟合结果较为可靠。
|
|
表 6 递增时段的DFA分析结果统计 Tab. 6 Statistics of DFA analysis at increasing period |
对比不同分阶段的变形趋势得出,对应序列在相应阶段处的趋势判断结果一致,但趋势程度具有一定的差异。在实际工程中,可综合考虑不同分阶段方式的结果,综合确定滑坡的变形趋势。
3 结语通过尖点突变理论在滑坡稳定性中的应用得出,该理论能很好地评价滑坡的稳定状态,有效反映滑坡各阶段的稳定性态。通过DFA分析对滑坡变形趋势的判断,得出滑坡整体及各阶段的变形趋势均呈持续增长趋势,且累计序列的趋势性要强于速率序列的趋势性,与滑坡稳定性的分析结果一致,说明该方法能准确判断滑坡的变形趋势,分析结果准确可靠。本文用两种方法分别判断滑坡稳定性及变形趋势,为滑坡防治提供了一定的依据。
| [1] |
柯福阳, 李亚云. 基于BP神经网络的滑坡地质灾害预测方法[J]. 工程勘察, 2014, 42(8): 55-60 (Ke Fuyang, Li Yayun. The Forecasting Method of Landslides Based on Improved BP Neural Network[J]. Geotechnical Investigation & Surveying, 2014, 42(8): 55-60)
(  0) 0) |
| [2] |
朱雷, 黄润秋, 王小群, 等. 基于滑带强度参数动态演化的滑坡稳定性研究[J]. 岩土力学, 2015, 36(S2): 431-438 (Zhu Lei, Huang Runqiu, Wang Xiaoqun, et al. Stability Study of Landslide Based on Dynamic Evolution of Sliding Surface Strength Parameter[J]. Rock and Soil Mechanics, 2015, 36(S2): 431-438)
(  0) 0) |
| [3] |
胡安龙, 王孔伟, 李建林, 等. 基于智能算法优化支持向量机模型的滑坡稳定性预测[J]. 自然灾害学报, 2016, 25(5): 1-10 (Hu Anlong, Wang Kongwei, Li Jianlin, et al. Prediction of Landslide Stability Based on SVM Model Optimized by Intelligent Algorithm[J]. Journal of Natural Disasters, 2016, 25(5): 1-10)
(  0) 0) |
| [4] |
张夏冉, 殷坤龙, 夏辉, 等. 渗透系数与库水位升降对下坪滑坡稳定性的影响研究[J]. 工程地质学报, 2017, 25(2): 488-495 (Zhang Xiaran, Yin Kunlong, Xia Hui, et al. Influence of Permeability Coefficient and Reservoir Water Level Fluctuation on Xiaping Landslide Stabilty[J]. Journal of Engineering Geology, 2017, 25(2): 488-495)
(  0) 0) |
| [5] |
李蔚, 盛德仁, 陈坚红, 等. 双重BP神经网络组合模型在实时数据预测中的应用[J]. 中国电机工程学报, 2007, 27(17): 94-97 (Li Wei, Sheng Deren, Chen Jianhong, et al. The Application of Double BP Neural Network Combined Forecasting Model in Real-Time Data Predicting[J]. Proceedings of the CSEE, 2007, 27(17): 94-97 DOI:10.3321/j.issn:0258-8013.2007.17.018)
(  0) 0) |
| [6] |
黄海峰, 易武, 易庆林, 等. 滑坡位移分解预测中的平滑先验分析方法[J]. 水文地质工程地质, 2014, 41(5): 95-100 (Huang Haifeng, Yi Wu, Yi Qinglin, et al. Smoothness Priors Approach in Displacement Decomposition and Prediction of Landslides[J]. Hydrogeology and Engineering Geology, 2014, 41(5): 95-100)
(  0) 0) |
| [7] |
史俊涛, 孔思丽, 贺俊, 等. 基于尖点突变理论的非均质土坡失稳判据分析[J]. 长江科学院院报, 2015, 32(5): 115-120 (Shi Juntao, Kong Sili, He Jun, et al. An Instability Criterion for Inhomogeneous Slope Based on Cusp Catastrophe Theory[J]. Journal of Yangtze River Scientific Research Institute, 2015, 32(5): 115-120)
(  0) 0) |
| [8] |
宋鑫华, 闫鸿浩. 基于尖点突变理论的浆砌块石边坡稳定性研究[J]. 岩土力学, 2016, 37(12): 3499-3505 (Song Xinhua, Yan Honghao. Analysis of Stability of Masonry Slope Based on Cusp Catastrophe Theory[J]. Rock and Soil Mechanics, 2016, 37(12): 3499-3505)
(  0) 0) |
| [9] |
张鑫, 蔡焕杰, 尹晓楠. 基于DFA的无定河径流长期变化趋势及持续性研究[J]. 生态环境学报, 2010, 19(1): 208-211 (Zhang Xin, Cai Huanjie, Yin Xiaonan. Long-Term Trends and Sustainability Analysis of Runoff in the Wuding River Basin[J]. Ecology and Environmental Sciences, 2010, 19(1): 208-211)
(  0) 0) |
| [10] |
佟春生, 黄强, 刘涵, 等. 黄河径流序列标度不变性分析及趋势预测研究[J]. 自然资源学报, 2007, 22(4): 86-86 (Tong Chunsheng, Huang Qiang, Liu Han, et al. Scale Invariant Analysis and Runoff Trend Prediction of the Runoff Time Series in the Yellow River[J]. Journal of Natural Resources, 2007, 22(4): 86-86)
(  0) 0) |
| [11] |
赵延林, 吴启红, 王卫军, 等. 基于突变理论的采空区重叠顶板稳定性强度折减法及应用[J]. 岩石力学与工程学报, 2010, 29(7): 1424-1434 (Zhao Yanlin, Wu Qihong, Wang Weijun, et al. Strength Reduction Method to Study Stability of Goaf Overlapping Roof Based on Catastrophe Theory[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(7): 1424-1434)
(  0) 0) |
| [12] |
周安康, 严宝文. 渭河流域月径流序列分形特征研究[J]. 水力发电学报, 2014, 33(4): 7-13 (Zhou Ankang, Yan Baowen. Fractal Characteristics of Monthly Runoff Process in Weihe River Watershed[J]. Journal of Hydroelectric Engineering, 2014, 33(4): 7-13)
(  0) 0) |
| [13] |
邬长福, 涂志刚, 万佳威, 等. 基于R/S分析与V/S分析的滑坡变形趋势判断及稳定性研究[J]. 水电能源科学, 2015, 33(1): 111-114 (Wu Changfu, Tu Zhigang, Wan Jiawei, et al. Judgment of Landslide Deformation Trends and Study of Landslide Stability Based on R/S and V/S Analysis[J]. Water Resources and Power, 2015, 33(1): 111-114)
(  0) 0) |
| [14] |
严超, 吕青. 基于二次指数平滑法和触发器的滑坡位移预测预警[J]. 武汉轻工大学学报, 2014, 33(4): 74-79 (Yan Chao, Lü Qing. Based on the Quadratic Exponential Smoothing and Trigger Landslide Displacement Prediction of Early Warning[J]. Journal of Wuhan Polytechnic University, 2014, 33(4): 74-79)
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38

