2. 辽宁科技大学土木工程学院,辽宁省鞍山市千山中路185号,114051
小波分析因其具有多分辨率的特点,在变形监测数据处理中得到广泛应用。小波分析的过程中, 一些因素会影响到去噪的效果,如小波函数、分解层数等。所以需要一些评价指标来指导小波的分解[1],从而达到最优的去噪效果。传统评价指标只有在真值已知的情况下才能准确判断小波去噪效果的优劣[2],而变形监测的数据其真值大多都是未知的,传统的评价指标不能满足去噪质量评价的要求。朱建军等[2]提出一种基于变异系数定权的去噪质量评价指标,其中选用均方根误差与平滑度两个指标,将两个指标归一化组成线性复合的评价指标。郭健等[3]利用均方根误差的变化量来判断小波去噪效果的优劣,根据均方根误差的变化是否趋于稳定来判定最优分解层数,变化量越小说明去噪的效果越好。李宗春等[4]提出将均方根误差变形量、互相关系数、信噪比以及平滑度4种评价指标归一化后求和作为总体评价指标来判定去噪效果的优劣,出现最大值时认为去噪效果最优。上述的方法虽然取得了一定的效果,但在真值未知的情况下,都在准确率以及简易程度上存在不同程度的缺陷。本文在总结前人经验的基础上,试图构建新的评价指标,使其能够准确地指导真值未知的情况下小波去噪的最佳分解层数,从而达到最佳的去噪效果。
1 传统评价指标小波去噪效果的优劣会受到小波函数及分解层数等因素的影响,由于不同的小波函数、不同的分解层数去噪后的效果都不尽相同,因此需要一些评价指标来衡量。常用的评价指标有均方根误差(RMSE)、信噪比(SNR)、平滑度(r)以及相关系数(R)[5]等。均方根误差主要是体现去噪信号与原始信号之间的偏差程度,其值越小,偏差度就越小,去噪效果越好;信噪比主要是体现噪声信号在整体信号中的比重,是原始信号能力与噪声能力的比值,其值越大去噪效果越好;平滑度主要是表述信号是否有局部的突变,平滑度越小,信号越光滑,去噪效果越好;相关系数主要是体现去噪后信号与原始信号的相似度,相关系数越接近1,说明去噪后所得到的信号与原始信号拟合得越好,去噪效果越好。
下面利用小波分析理论对真值已知和真值未知的两种信号进行去噪处理。由于变形监测数据是一种非平稳的信号,本文采用3个不同频率的正弦信号以及一个低频趋势信号叠加组成的模拟变形数据M(式(1))作为真值已知的信号,在原始信号的基础上添加信噪比为6 dB的高斯白噪声,采集点数为1 024;真值未知的信号为抚顺市某广场的C1点沉降观测信号,共256期,选取sym4小波函数,采用软阈值函数,分解层数为1~8层,然后通过上述4种传统指标进行最优分解层数的判定。
| $\begin{array}{l} M = 3\sin \left( {2{\mathit{p}_\mathit{t}}/500} \right) + 2\sin \left( {2{p_t}/200} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\sin \left( {2{p_t}/50} \right) + 0.001t \end{array} $ | (1) |
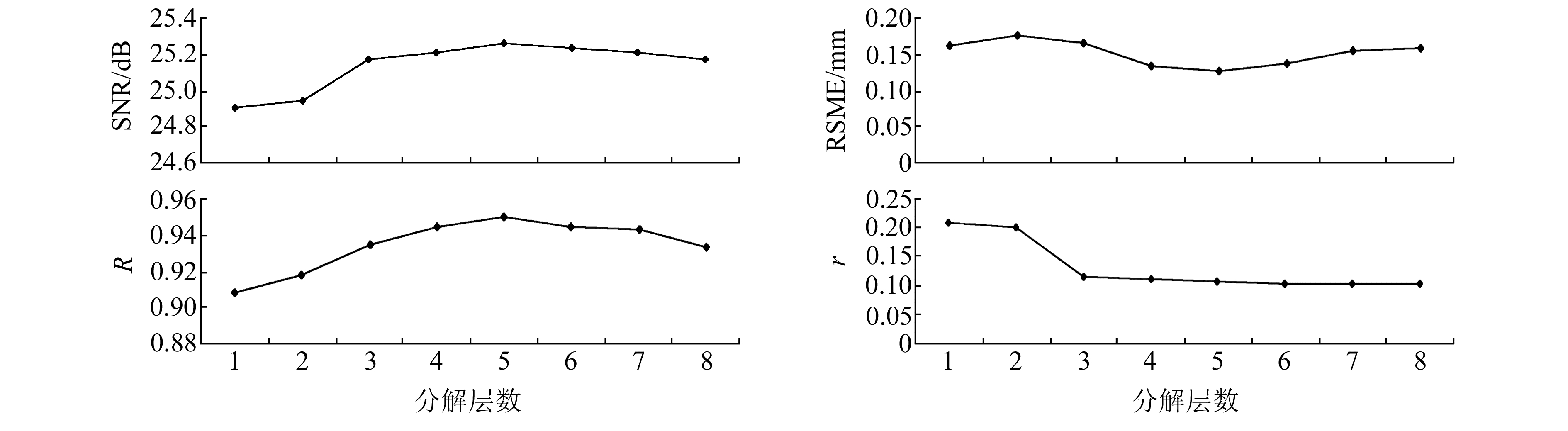
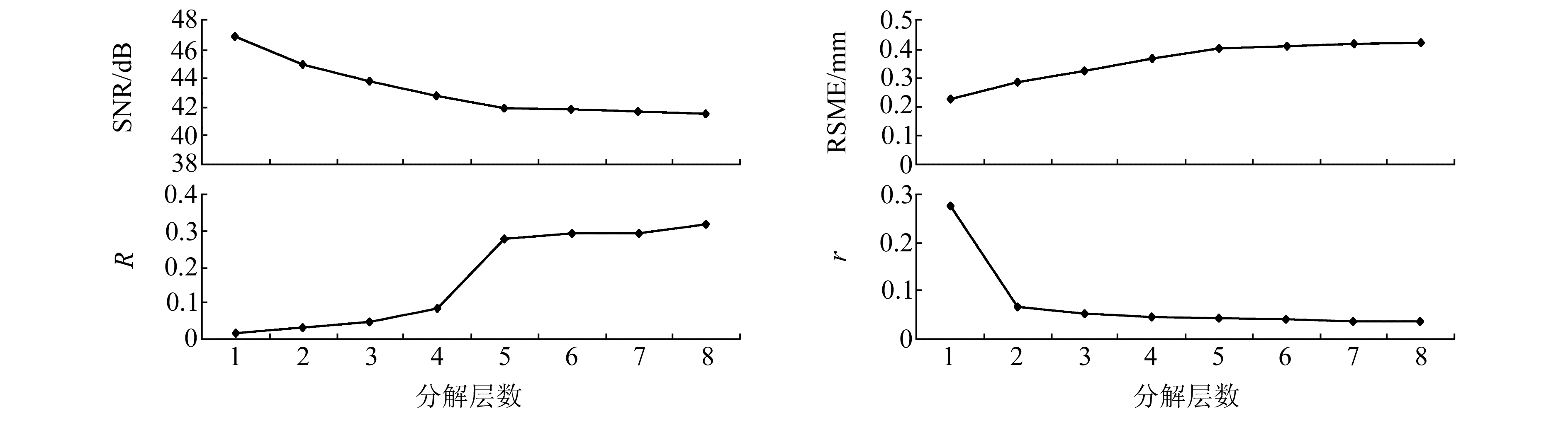
图 1为真值已知的条件下小波去噪的评价结果。可以看出,均方根误差、信噪比以及相关系数确定最优分解层数为5层,平滑度无法判定。图 2为真值未知的条件下小波去噪的评价结果。由图可知,4种传统评价指标都不能准确地确定最优分解层数,信噪比和平滑度随着分解层数的增加而减小,而均方根误差和相关系数随分解层数的增加而增大,都没有收敛到某一个固定的数值,这显然不符合实际情况。因此,在真值未知的情况下,传统的评价指标都不能满足小波去噪质量评价需求。
|
图 1 4种传统评价指标对模拟变形数据M去噪效果的评价结果 Fig. 1 Evaluation results of the four traditional evaluation indexes on M simulation of deformation data |
|
图 2 4种传统评价指标对沉降信号去噪效果的评价结果 Fig. 2 Evaluation results of the four traditional evaluation indexes on settlement signals de-noising |
传统的评价指标在真值未知的情况下不能很好地满足质量评价要求,其原因如下:1)实测的信号真值是未知的,故去噪后的信号不能直接通过与原始信号比较来描述去噪的效果,通过定量分析无法满足去噪评价的要求;2)由于变形监测的信号整体有一个变化趋势,而传统的评价指标没有考虑到这个变化趋势[6]。如果能选出一些能够描述去噪后信号的整体变化趋势的评价指标,然后通过一定的办法将这些指标进行复合, 根据变化率特征[7]采用定性分析的方法来指导小波分解,从而满足在真值未知的情况下小波去噪质量评价的要求,这就是本文提出的复合评价指标的基本原理。
2.1 指标的选取均方根误差、信噪比、相关系数都是描述去噪信号的细节上的信息[8],而平滑度主要就是关注信号整体的变化趋势,所以必须选用平滑度这个指标。信噪比和平滑度的变化趋势一致,具有重叠性,同时,相关系数主要是体现去噪信号与理论信号的拟合程度,而理论信号是未知的,准确度不高,故本文选择均方根误差及平滑度两个指标。由于原始信号真值未知,去噪后的信号不能直接通过与原始信号比较来描述去噪的效果。为此,根据变化率特征重新构造两个指标:均方根误差变化量(VR)及平滑度变化量(Vr)。具体表达式见文献[2]。
2.2 复合指标的构建因为两个指标基数范围不一样,为了便于比较,将两个指标归一化到[0, 1]区间[5]。
均方根误差变化量归化公式为:
| ${P_{{\mathit{V}_\mathit{R}}}}\left( \mathit{k} \right) = \frac{{{\mathit{V}_{{\mathit{R}_{{\rm{max}}}}}} - {\mathit{V}_\mathit{R}}\left( \mathit{k} \right)}}{{{V_{{R_{\max }}}} - {V_{{R_{\min }}}}}} $ | (2) |
平滑度变化量归化公式为:
| ${P_{{\mathit{V}_\mathit{r}}}}\left( \mathit{k} \right) = \frac{{{\mathit{V}_\mathit{r}}\left( k \right) - {\mathit{V}_{{\mathit{r}_{{\rm{max}}}}}}}}{{{V_{{r_{\max }}}} - {V_{{r_{\min }}}}}} $ | (3) |
式(2)、式(3)中,PVR(k)、PVr(k)分别表示均方根误差变化量以及平滑度变化量的归一化结果,k表示小波分解的尺度,VRmax、VRmin、Vrmax、Vrmin分别表示均方根误差变化量以及平滑度变化量的最大值和最小值。
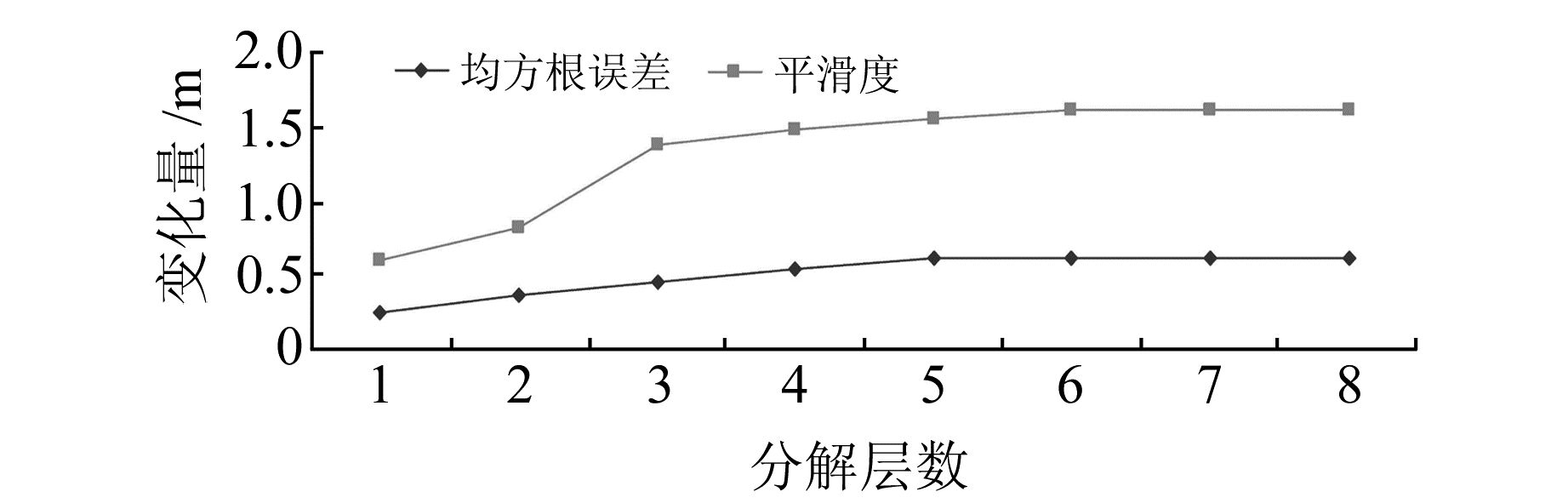
实际中,均方根误差变形量和平滑度变形量随着分解层数的增加均表现出明显的收敛特性,即使过分去噪,上述两个指标的变化都不大。图 3选取抚顺市某广场的C1点沉降观测信号,使用sym4小波函数,通过1~8层分解去噪,得到均方根误差变化量和平滑度变化量归一化后的变化趋势。可以看出,平滑度变化量以及均方差误差变化量分解层数分别达到6层和5层后,两个指标都存在收敛且变化率均趋于平缓,而这种变化趋势也恰好符合变形数据的变化趋势。为了更全面地反映信号的变化特征,本文对两种指标进行复合。
|
图 3 均方根误差变化量以及平滑度变化量 Fig. 3 Root mean square error variation and smoothness variation |
由于两个指标反映信号特征的程度不同,在复合过程中所占的权重也不一样,因此,要对两者进行赋权操作。本文采用熵权[9-10]定权的方法。两个指标权值计算过程见文献[9-10]。
最后,通过线性组合的方式得到加权复合指标S,其表达式为:
| $S={{w}_{{{P}_{{{V}_{R}}}}}}\left( k \right){{P}_{{{V}_{R}}}}\left( k \right)+{{w}_{{{P}_{{{V}_{r}}}}}}\left( k \right){{P}_{{{V}_{r}}}}\left( k \right) $ | (4) |
式中,wPVR(k)、wPVr(k)分别表示由熵值计算得到的均方根误差变化量以及平滑度变化量的权重,PVR(k)、PVr(k)分别表示均方根误差变化量以及平滑度变化量的归一化结果。
从图 3可知,随着分解层数的增加,两个指标都存在收敛特性,即达到最佳分解层数后,变化率明显降低并趋于稳定。因此,该复合指标在指导小波去噪的过程中,当达到某一分解层数时,其数值的变化率开始降低且趋于平稳,该层数即为指导的最优分解层数。
3 算例分析与比较利用实际的观测信号进行小波去噪处理,信号来源是抚顺市某广场的C1点256期沉降观测数据。选取sym4小波基函数,采用软阈值方法,分解层数为1~8层,然后采用文献[2]指标T、文献[3]指标r、文献[4]指标H以及本文提出的指标S进行最优分解层数的判定,实验结果如表 1所示。
|
|
表 1 不同分解层数的4种评价指标数据 Tab. 1 Four index data of the different decomposition level |
从表 1可以看出,文献[3]的评价指标r在第7层达到最小值,文献[4]的评价指标H在第7层达到最大值,因此,两种指标指导的最优分解层数为7层;文献[2]评价指标T在第4层达到最小值,因此,最优分解层数为4层;本文提出的评价指标S从第5层开始数值变化率降低且趋于平稳,因此,最优分解层数为5层。4种指标所评定最优的分解层数不同,那么哪种指标评定的分解层数才是最优的,还需要进一步分析。
本文可以根据这种关系将4种指标指导的小波去噪后所得到的信号中的前10个数据,利用灰色GM(1, 1)原理[11]分别建立预测模型,预测模型的精度越高,说明指标指导小波去噪效果越好,指标评定的分解层数就是最优的。由于篇幅有限,灰色GM (1, 1)建模过程见文献[12]。
根据预测模型等级要求,对各指标指导的小波去噪后的数据所建立的预测模型进行等级评定。评定结果如表 2所示。
|
|
表 2 4种指标指导小波去噪后信号建立预测模型的精度等级 Tab. 2 Four indexes guide the wavelet de-noising signal to establish the accuracy grade of the prediction mode |
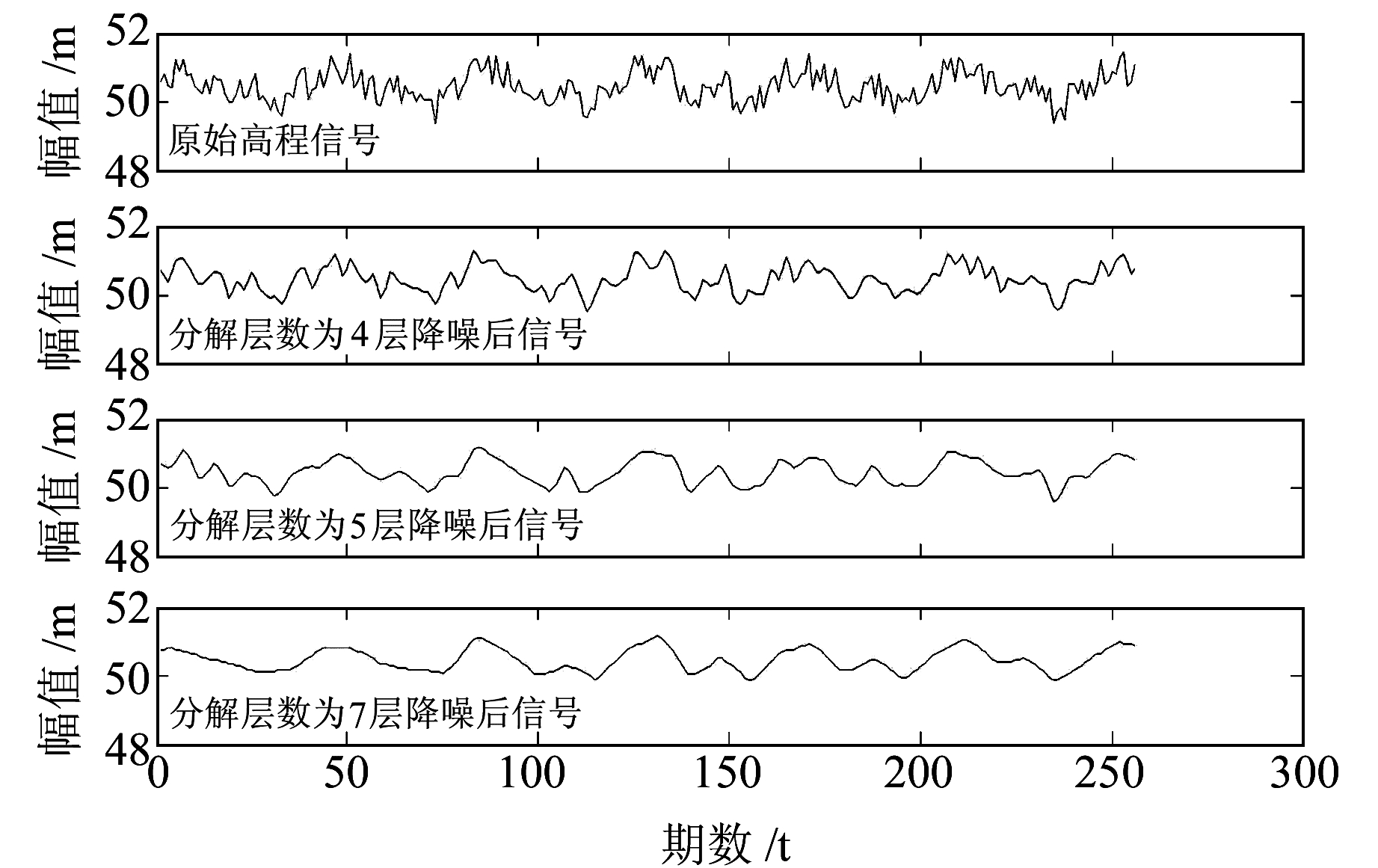
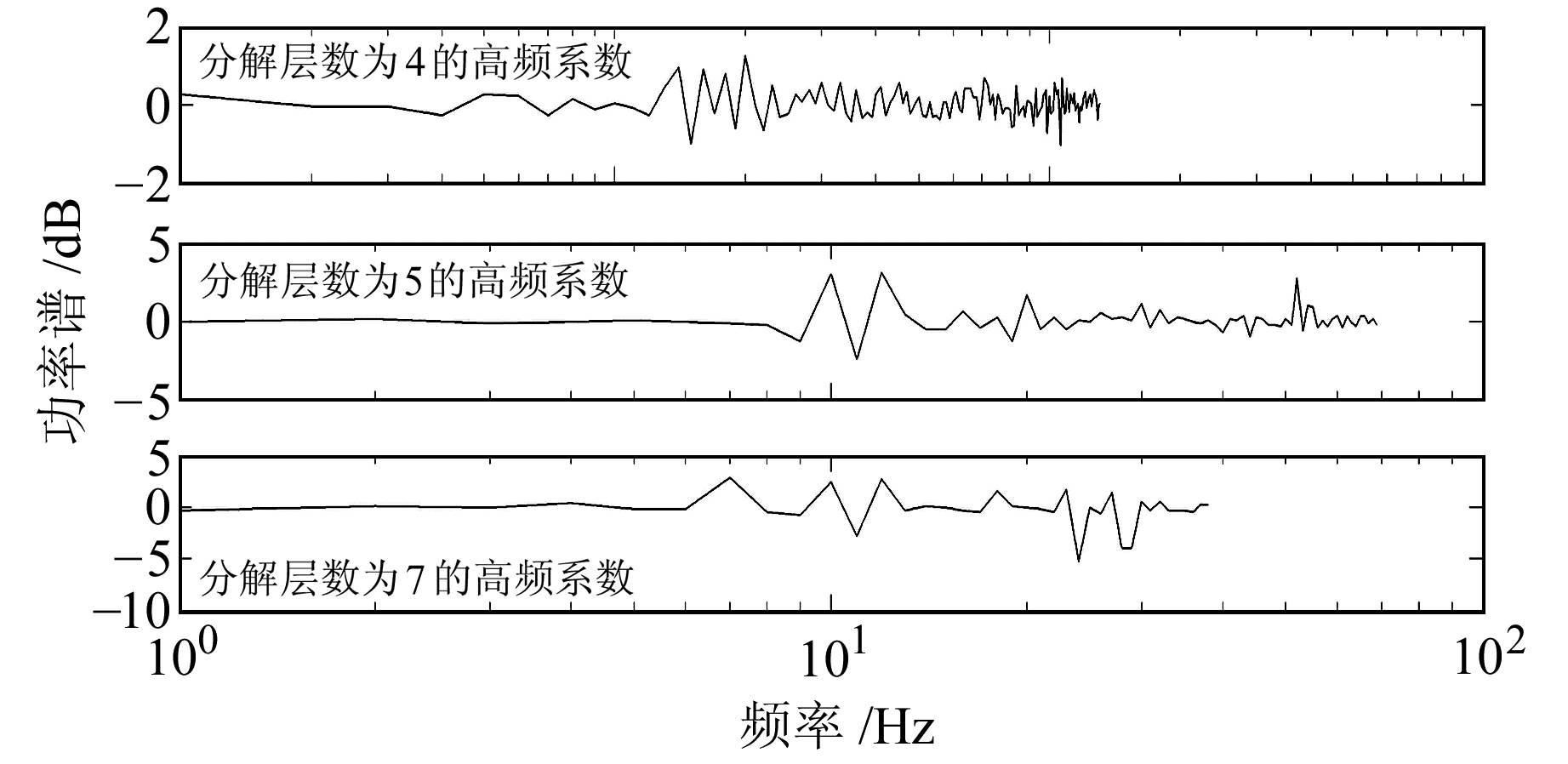
从表 2可以看出,H、r两个指标指导分解后的信号建立的预测模型都没有原始信号所建立的预测模型精度高,这就说明指标H及r进行了错误的指导。指标T指导分解后的信号及原始信号所建立的预测模型精度等级是相同的,都没有达到优秀,同时也说明了小波分解层数为4没有达到去噪的效果。本文提出的指标S指导后建立的预测模型的C及P值都满足等级是优的条件,因此,小波去噪最优分解层数为5层,本文提出的指标S进行了小波去噪最优分解层数正确的指导。从图 4还能看出,分解层数为7层时,降噪后的信号过于光滑已经失去了原有信号的变化趋势。这是因为分解层数过高,有用部分的高频部分系数会被滤掉,使去噪后的信号失真。分解层数为4层降噪后的信号比较粗糙,这是因为分解过程不够彻底,很多带有高频部分的系数保留在低频部分里了。分解层数为5层时在降噪过程中不仅能够使有用部分的高频系数保持原有信号的变化趋势,还能很好地去掉保留在低频部分里的带有噪声的高频系数,使去噪后的信号光滑,所以分解层数为5层降噪效果最好。图 4也能够很好地说明本文提出的指标S能够对小波去噪的最优分解层数进行了正确的指导,从而达到最佳的去噪效果。图 5为不同分解层数所得到的高频系数的功率谱密度估计图,同分解层数为4相比,5层分解后更好地剔除了101 Hz以下以及102 Hz以上的无用高频系数。同时与分解层数为7相比,对101~102 Hz之间的有用高频系数适当地进行保留,同样可以证明分解5层降噪效果最好。
|
图 4 不同分解层数的小波去噪效果图 Fig. 4 De-noising effect drawing of the different decomposition level |
|
图 5 功率谱密度 Fig. 5 Power spectrum density |
除此之外,本文还使用文献[5]提出的方法进行评价,所得到的结果与本文分析的结果一致。但文献[5]的方法需要画图进行拐点识别,评价过程稍显复杂,并且该方法需要3个指标进行复合,计算过程比较繁琐。综合分析,本文提出的S评价指标相比现有的方法计算更简便、更科学、更准确,不再通过定量分析的方法,而是借助变化率特征,采用定性分析的方法来指导小波分解,能够满足真值未知情况下去噪质量的评价要求。
为进一步验证复合指标S的可靠性,再对一组真值未知的变形监测数据进行小波去噪处理。信号来源为CORS数据处理站进行连续测量所得原始高程数据,采样间隔为2s,共观测1 236个历元。选取sym4小波基函数,采用软阈值方法,分解层数为1~8层,然后利用复合指标S判定最优分解层数,将分解层数对应的指标数据列于表 3。
|
|
表 3 各分解层数的评价指标数据 Tab. 3 Evaluation indexes date of each decomposition level |
从表 3可以看到,分解层数为5时,S数值变化率开始降低且趋于平稳,因此,根据判定规则,去噪的最优分解层数为5。利用5层分解去噪后得到的信号前10个数据建立灰色GM(1, 1)预测模型,预测模型的精度如表 4所示。
|
|
表 4 5层分解后的信号建立预测模型精度等级 Tab. 4 The signal of 5 layer decomposition establish accuracy grade of the prediction model |
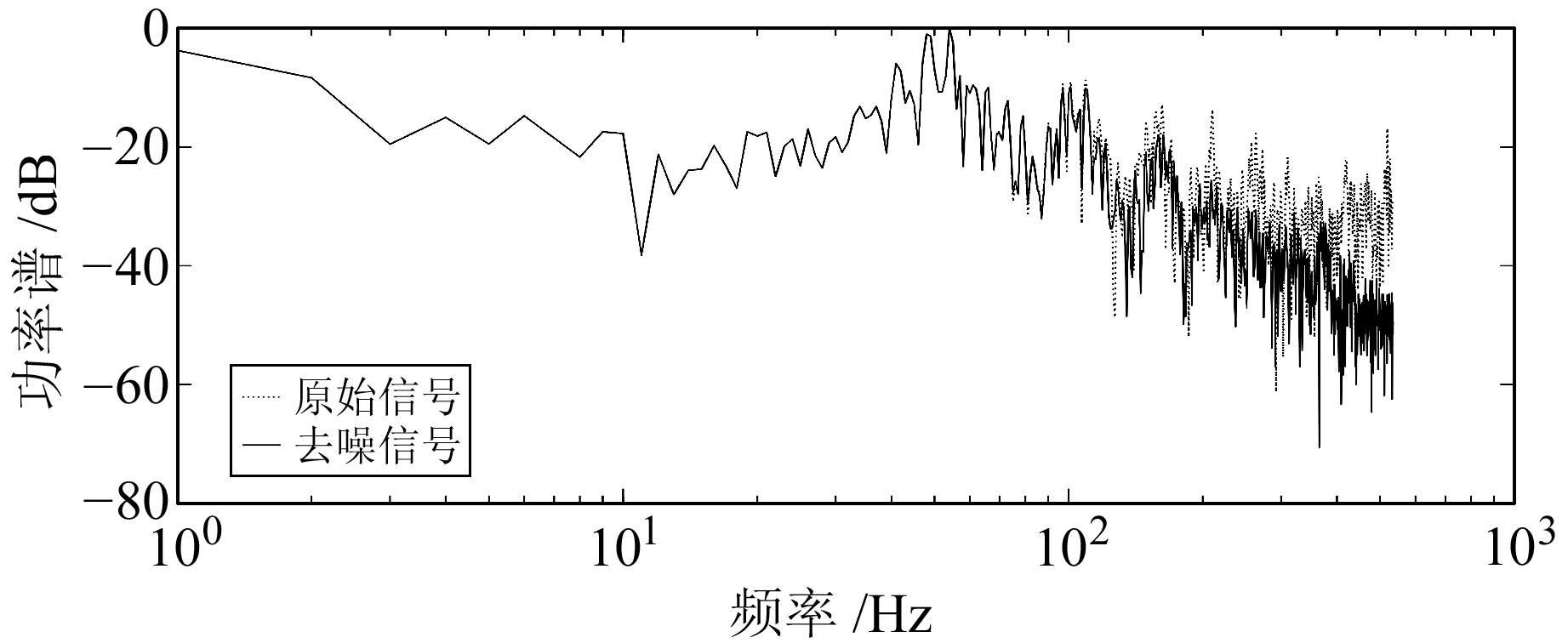
进行5层小波去噪后得到的高程信号所建立的预测模型的精度等级是优,建模后的C及P值都满足等级优的条件,这就证明了本文提出的复合指标S对小波去噪的最优分解层数进行了正确的指导。图 6为原始高程信号与分解层数为5的去噪信号。可以看出,去噪后的信号不仅保留了原始信号的变化趋势,而且还剔除了带有误差的高频无用信息,使去噪后的信号变得光滑,达到了最佳去噪的效果。图 7为原始信号和5层分解去噪后信号的功率谱密度估计图。可以看出,5层分解后保留了102 Hz以下的低频有用信息,同时剔除了102 Hz以上的无用高频信息,还对101~102 Hz中间的有用高频信息进行了适当的保留,同样证明了复合指标S对小波去噪的最优分解层数进行了正确的指导。由于篇幅有限,在此就不列举其他各层的效果图及其频谱图。

|
图 6 分解层数为5的小波去噪效果 Fig. 6 De-noising effect drawing of five decomposition levels |
|
图 7 功率谱密度 Fig. 7 Power spectrum density |
本文给出了一种真值未知的情况下小波去噪质量评价的方法,通过熵权法定权将归一化后的均方误差变化量与平滑度变化量进行线性组合。将该方法用于实际工程中,得到了满意的结果。该方法有两个特点:1)主要考虑了信号本身变化率特征来确定小波去噪评价指标,在真值未知的情况下可以有效地识别去噪的最优分解层数。2)计算简便快捷且准确率更高,不再采用定量分析的方法,而是采用定性分析的方法来判定最优分解层数,能够满足在真值未知的情况下去噪质量的评价要求,为小波分析在测量数据处理中的应用提供一种可靠的评价指标。
| [1] |
王中元, 周天强, 张鹏飞. 高层建筑物GPS动态变形监测数据处理[J]. 测绘科学, 2012, 37(1): 47-50 (Wang Zhongyuan, Zhou Tianqiang, Zhang Pengfei. GPS Dynamic Deformation Monitoring on High-Rise Buildings[J]. Science of Surveying and Mapping, 2012, 37(1): 47-50)
(  0) 0) |
| [2] |
朱建军, 章浙涛, 匡翠林, 等. 一种可靠的小波去噪质量评价指标[J]. 武汉大学学报:信息科学版, 2015, 40(9): 688-693 (Zhu Jianjun, Zhang Zhetao, Kuang Cuilin, et al. A Reliable Evaluationg Indicator of Wavelet De-Noising[J]. Geomatics and Information Science of Wuhan University, 2015, 40(9): 688-693)
(  0) 0) |
| [3] |
郭健, 查吕应, 庞有超. 基于小波分析的深基坑地表沉降预测研究[J]. 岩土工程学报, 2014, 36(增2): 343-347 (Guo Jian, Zha Lüying, Pang Youchao. Prediction for Ground Settlement of Deep Excavations Based on Wavelet Analysis[J]. Hinese Journal of Geotechnical Engineering, University, 2014, 36(S2): 343-347)
(  0) 0) |
| [4] |
李宗春, 邓勇, 张冠宇, 等. 变形测量异常数据处理中小波变换最佳级数的确定[J]. 武汉大学学报:信息科学版, 2011, 36(3): 285-288 (Li Zongchun, Deng Yong, Zhang Guanyu, et al. Determination of Best Grading of Wavelet Transform in Deformation Measurement Data Filtering[J]. Geomatics and Information Science of Wuhan University, 2011, 36(3): 285-288)
(  0) 0) |
| [5] |
陶珂, 朱建军. 多指标融合的小波去噪最佳分解尺度选择方法[J]. 测绘学报, 2012, 41(5): 749-755 (Tao Ke, Zhu Jianjun. A Hybrid Indicator for Determining the Best Decomposition Scale of Wavelet Denoising[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 749-755)
(  0) 0) |
| [6] |
黄其欢, 岳建平. 地基InSAR新技术及水利工程变形监测应用[J]. 辽宁工程技术大学学报, 2015, 34(3): 386-389 (Huang Qihuan, Yue Jianping. A New Technology of Ground-Based InSAR and Its Application to Hydraulic Engineering Deformation Monitoring[J]. Journal of Liaoning Technical University, 2015, 34(3): 386-389)
(  0) 0) |
| [7] |
Xu K J, Wang X F, Li Y S. Fundamental Wave Extraction and Frequency Measurement Based on IIR Wavelet Filter Banks[J]. Measurement, 2007, 40(6): 665-671 DOI:10.1016/j.measurement.2006.07.010
(  0) 0) |
| [8] |
张德丰. Matlab小波分析[M]. 北京: 机械工业出版社, 2009 (Zhang Defeng. Matlab Wavelet Analysis[M]. Beijing: China Machine Press, 2009)
(  0) 0) |
| [9] |
吴奕, 朱海兵, 周志成. 基于熵权模糊物元和主元分析的变压器状态评价[J]. 电力系统保护与控制, 2015, 43(17): 1-6 (Wu Yi, Zhu Haibing, Zhou Zhicheng.. Transformer Condition Assessment Based on Entropy Fuzzy Matter-Element and Principal Component Analysis[J]. Power System Protection and Control, 2015, 43(17): 1-6 DOI:10.7667/j.issn.1674-3415.2015.17.001)
(  0) 0) |
| [10] |
罗毅, 李昱龙. 基于熵权法和灰色关联分析法的输电网规划方案综合决策[J]. 电网技术, 2013, 37(1): 77-80 (Luo Yi, Li Yulong. Comprehensive Decision-Making of Transmission Network Planning Based on Entropy Weight and Grey Relational Analysis[J]. Power System Technology, 2013, 37(1): 77-80)
(  0) 0) |
| [11] |
周伟萍, 王丰效. 灰色DNGM(1, 1)预测模型及其优化[J]. 计算机工程与应用, 2013, 49(10): 28-31 (Zhou Weiping, Wang Fengxiao. DNGM(1, 1)Model and Its Parameters Optimal[J]. Computer Engineering and Applications, 2013, 49(10): 28-31 DOI:10.3778/j.issn.1002-8331.1202-0322)
(  0) 0) |
| [12] |
王利, 张勤, 张显云. 基于均值滤波的灰色预测模型及其应用[J]. 西安科技大学学报, 2008, 28(1): 67-71 (Wang Li, Zhang Qin, Zhang Xianyun. Application of Object-Oriented Analysis Models in Expert System of Welding Process Planning[J]. Journal of Xi'an University of Science and Technology, 2008, 28(1): 67-71)
(  0) 0) |
2. College of Civil Engineering, University of Science and Technology Liaoning, 185 Mid-Qianshan Road, Anshan 114051, China
 2018, Vol. 38
2018, Vol. 38


