2. 北京国研数通软件技术有限公司,北京市朝内大街298号,100010
地震精密水准测量是地震预测预报工作的手段之一,由于其测量精度在垂向上具有远超其他手段的优越性,在进行地震同震、地表垂直形变等方面的研究工作中发挥着重要的作用[1-2]。而由于地震精密水准网存在多余观测,为了消除观测结果不符值,进行平差计算是必不可少的一个环节。一般地,通过条件平差法或间接平差法即可满足地震精密水准网的平差计算,然而这种传统的算法效率低下,当网型较大、观测边数较多时,计算非常耗时。
本文在深入研究地震精密水准数据特性的基础上发现,组成基础方程的系数矩阵仅由1、-1和0三个数值组成,若精密水准网有m条边、n个点,则构建的基础方程系数恰好由m个1、n个-1以及mn-m-n个0构成,且基础方程系数每行有且仅有一个1、一个-1,其余的位置均为0。除此之处,平差方程的法方程系数恰好又为对称正定矩阵。基于此,本文在计算法方程时,通过只对“非零值”进行计算以及利用变量循环重新编号法[3]减少矩阵的计算次数,从而提高计算效率。
1 算法原理假设区域精密水准网共有m条边、n个点,权阵为P,误差方程系数矩阵为A,常数项矩阵为L,未知数矩阵为X,则有:
| $ \mathit{\boldsymbol{P = }}\left| \begin{array}{l} {p_1}\;\;\;\;\;0\;\;\;\;\;0\;\;\;\;\; \cdots \;\;\;\;\;0\\ \;0\;\;\;\;\;{p_1}\;\;\;\;0\;\;\;\;\; \cdots \;\;\;\;\;0\\ \;0\;\;\;\;\;\;0\;\;\;\;{p_3}\;\;\;\; \cdots \;\;\;\;\;0\\ \cdots \;\;\; \cdots \;\;\; \cdots \;\;\; \cdots \;\;\;\; \cdots \\ \;0\;\;\;\; \cdots \;\;\; \cdots \;\;\; \cdots \;\;\;\;{p_m} \end{array} \right|, \mathit{\boldsymbol{L}} = \left| \begin{array}{l} {l_1}\\ {l_2}\\ {l_3}\\ \cdots \\ {l_m} \end{array} \right|, \mathit{\boldsymbol{X}} = \left| \begin{array}{l} {x_1}\\ {x_2}\\ {x_3}\\ \cdots \\ {x_n} \end{array} \right| $ | (1) |
式中,pi=1/si(i=1, 2, …, m)。
下面考虑误差方程系数A。已知
| $ \mathit{\boldsymbol{A}} = \left| {\begin{array}{*{20}{l}} {{a_{11}}\;\;\;\;{a_{12}}\;\;\;\;{a_{13}}\;\;\;\; \cdots \;\;\;\;{a_{1n}}}\\ {{a_{21}}\;\;\;\;{a_{22}}\;\;\;\;{a_{23}}\;\;\;\; \cdots \;\;\;\;{a_{2n}}}\\ {{a_{31}}\;\;\;\;{a_{32}}\;\;\;\;{a_{33}}\;\;\;\; \cdots \;\;\;\;{a_{3n}}}\\ { \cdots \;\;\;\; \cdots \;\;\;\;\; \cdots \;\;\;\; \cdots \;\;\;\; \cdots }\\ {{a_{m1}}\;\;\; \cdots \;\;\;\;\; \cdots \;\;\;\; \cdots \;\;\;{a_{mn}}} \end{array}} \right| $ |
令Ai=|ai1ai2 … ain|,其中i=1, 2, …, m。根据地震区域精密水准网方程的特性可知,Ai所对应的线路中仅含有一个起点、一个终点,即-Po起点+Po终点=H高差。因此,当组建成误差方程矩阵反映到矩阵Ai中时,Po起点系数在Ai中相应位置上的值为-1,Po终点相应位置上的值为1,其余位置上的值皆为0。则A中非0值的个数共有2m个,总数只占整个矩阵A的2/n。
已知间接平差的法方程表达式为[4]:
| $ {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PAX}} - {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PL}} = 0 $ | (2) |
且传统的平差算法表达式为:
| $ \mathit{\boldsymbol{X}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PA}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PL}} $ | (3) |
当得到式(2)后,如果不直接利用其计算X,而是对ATPA和ATPL作进一步的数学推导,在此基础上再对X进行计算,则可以避免前述的“零值累加”的无效运算。经推导可知:
| $ {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PL = }}{\left| {\sum\limits_{i = 1}^m {{a_{i1}}{p_i}{l_i}\;\;\;\;\sum\limits_{i = 1}^m {{a_{i2}}{p_i}{l_i}\;\;\;\; \cdots \;\;\;\;\sum\limits_{i = 1}^m {{a_{im}}{p_i}{l_i}} } } } \right|^{\rm{T}}} $ | (4) |
| $ {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PA = }}\left| \begin{array}{l} \sum\limits_{i = 1}^m {{a_{i1}}{a_{i1}}{p_i}\;\;\;\;\sum\limits_{i = 1}^m {{a_{i1}}{a_{i2}}{p_i}\;\;\;\; \cdots \;\;\;\;\sum\limits_{i = 1}^m {{a_{i1}}{a_{in}}{p_i}} } } \\ \sum\limits_{i = 1}^m {{a_{i1}}{a_{i2}}{p_i}\;\;\;\;\sum\limits_{i = 1}^m {{a_{i2}}{a_{i2}}{p_i}\;\;\;\; \cdots \;\;\;\;\sum\limits_{i = 1}^m {{a_{i2}}{a_{in}}{p_i}} } } \\ \;\;\;\;\;\; \cdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdots \;\;\;\;\;\;\;\;\; \cdots \;\;\;\;\;\;\;\;\;\; \cdots \;\;\;\;\;\\ \sum\limits_{i = 1}^m {{a_{i1}}{a_{in}}{p_i}\;\;\;\;\sum\limits_{i = 1}^m {{a_{i2}}{a_{in}}{p_i}\;\;\;\; \cdots \;\;\;\;\sum\limits_{i = 1}^m {{a_{in}}{a_{in}}{p_i}} } } \end{array} \right| $ | (5) |
由式(4)可以看出,任何一个A (i, j)(i=1, 2, …, m; j=1, 2, …, n)在表达式中仅出现一次,而A共有2m个非零值,因此在进行逐行遍历时ATPL只需要计算2m次,并将计算结果在相应位置上累加即可。对于式(5),假定Ai中A (i, l)和A (i, k)(l, k∈(1, 2, …, n))为非零值,则对第Ai行进行遍历时,仅能够对ATPA中的ATPA (l, l)、ATPA (k, k)以及ATPA (l, k)产生贡献(计算结果不为零),即每遍历一行,只需要计算3个值即可,换言之,即计算3次。而A共有m行,需要遍历m次,因此共需要计算3m次。
综上所述,无论是计算A TPL还是A TPA,当按照水准路线进行逐行遍历时,只需要针对值为不为0的系数进行计算并在相应的位置上累加即可,而不需要像传统的方法那样进行逐项乘积并累加,从而避免进行大量关于“零值累加”的计算,导致运算效率降低。表 1为一般平差算法和高效算法在进行ATPL和ATPA运算次数上的比较。
|
|
表 1 ATPL与ATPA运算次数对比 Tab. 1 Comparison between ATPL and ATPA |
进一步不难发现,ATPA矩阵为对称正定矩阵,只需要计算该矩阵的下三角或上三角矩阵即可,且考虑到ATPA为对称正定矩阵,为简化程序编写过程,提高计算效率,可选用变量循环重新编号法进行求逆,这种算法与Gauss约化法、Gauss-Jordan消去法相比,虽然多占用一些内存,但是计算效率更高[5]。
2 算例利用C#语言在VS2010平台上编写程序,选用2个算例并分别利用2种算法进行测试。算例1选用了模拟数据,如图 1所示,模拟数据共计16条边,9个点(P1为已知点,Hp1=0 mm,详细信息见表 2)。
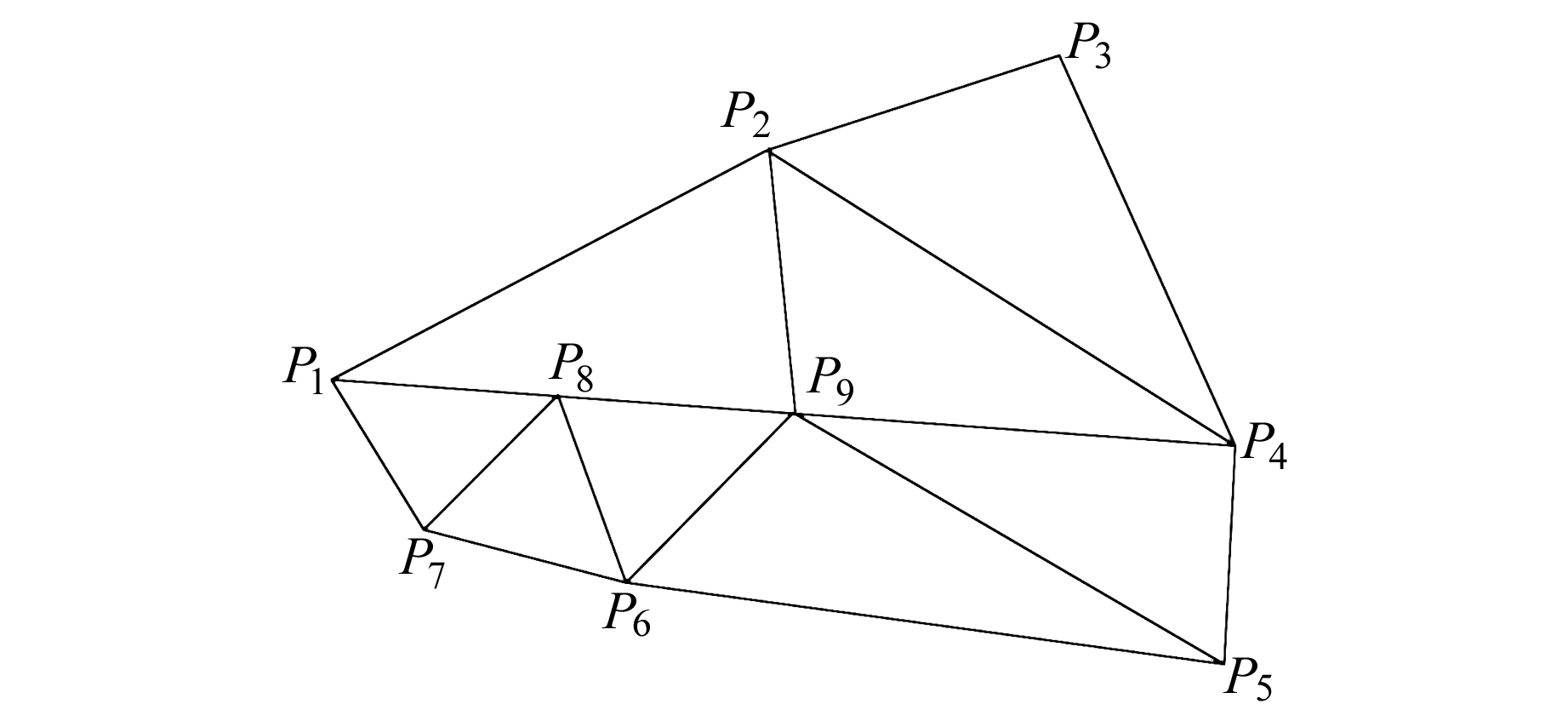
|
图 1 模拟算例1 Fig. 1 Numerical example 1 |
|
|
表 2 模拟算例1 Tab. 2 Numerical example 1 |
由表 3看出,两种方法计算结果完全一致,但计算时间上(精确至整数位)差别较大(表 4),其中传统算法耗时10 ms,而高效算法接近0 ms。
|
|
表 3 模拟算例1平差计算结果 Tab. 3 Adjustment results of numerical example 1 |
|
|
表 4 算法对比 Tab. 4 Comparison of the two algorithms |
算例2选用天津市滨海新区某年精密水准网数据进行计算,如图 2所示。该水准网共428条边,410个点,分别选用2种算法进行计算。计算结果表明,2种算法结果完全一致,单位权中误差均为0.000 8 mm(由于数据量较大,未在本文中列出),但在计算耗时方面(表 4),二者相差21 969 ms。
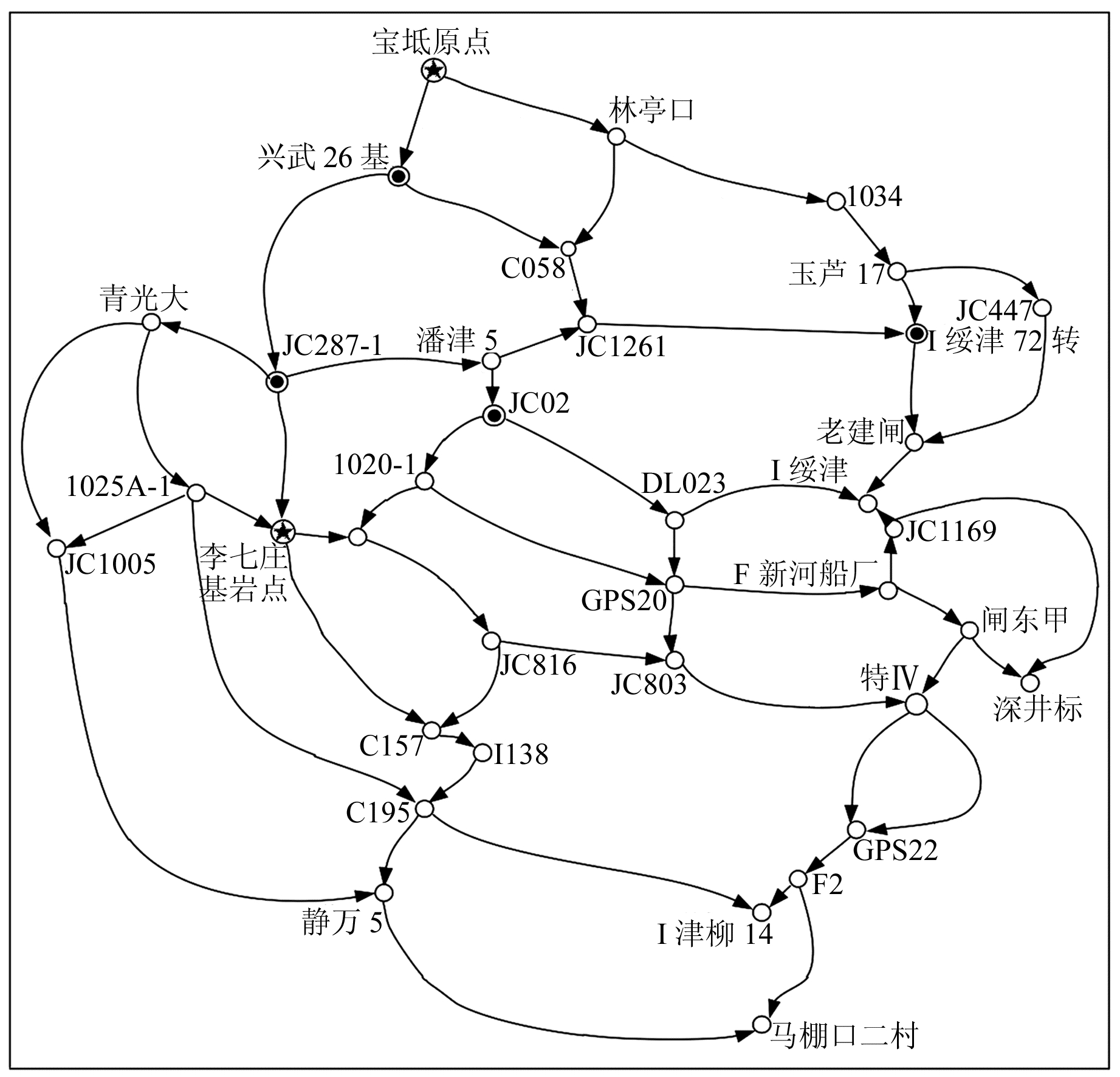
|
图 2 天津市滨海新区精密水准网 Fig. 2 Precise leveling network in Binhai district of Tianjin |
根据地震区域精密水准网的特点,在进行平差运算时,通过只对矩阵中非零值进行计算并累加,避免了进行大量零值的无效累加运算,提高了运算效率。同时,考虑到地震区域精密水准网平差法方程系数为对称正定矩阵,利用变量循环重新编号法且仅存储下三角矩阵的形式,进一步提高了运算效率。
| [1] |
王双绪, 蒋锋云, 张四新, 等. 六盘山及其邻区现今大地垂直形变与构造活动研究[J]. 大地测量与地球动力学, 2016, 37(1): 16-21 (Wang Shuangxu, Jiang Fengyun, Zhang Sixin, et al. Present Vertical Deformation and Tectonic Activity in Liupanshan and Its Adjacent Areas[J]. Journal of Geodesy and Geodynamics, 2016, 37(1): 16-21)
(  0) 0) |
| [2] |
刘琦, 闻学泽, 邵志刚. 基于GPS、水准和强震动观测资料联合反演2013年芦山7.0级地震同震滑动分布[J]. 地球物理学报, 2016, 59(6): 2113-2125 (Liu Qi, Wen Xueze, Shao Zhigang. Joint Inversion for Coseismic Slip of the 2013 MS7.0 Lushan Earthquake from GPS, Leveling and Strong Motion Observations[J]. Chinese J Geophys, 2016, 59(6): 2113-2125 DOI:10.6038/cjg20160617)
(  0) 0) |
| [3] |
郭显娥. 程序实现对称正定矩阵的求逆[J]. 雁北师院学报, 1998, 14(5): 11-15 (Guo Xian'e. The Settlement of the Inversion Operation on the Procedure of the Symmetric Matrix[J]. Journal of Yanbei Normal University, 1998, 14(5): 11-15)
(  0) 0) |
| [4] |
陶本藻. 误差理论与测量平差基础[M]. 武汉: 武汉大学出版社, 2009 (Tao Benzao. Error Theory and Measurement Adjustment Basis[M]. Wuhan: Wuhan University Press, 2009)
(  0) 0) |
| [5] |
许松钧. 大型对称正定矩阵求逆算法的选择[J]. 昆工科技, 1991(1): 1-5 (Xu Songjun. Selection of Inverse Algorithm for Large Symmetric Positive Definite Matrices[J]. Kunming Science and Technology, 1991(1): 1-5)
(  0) 0) |
2. SRIT Software Technology Co Ltd, 298 Chaonei Street, Beijing 100010, China
 2018, Vol. 38
2018, Vol. 38

