GPS/BDS组合定位较单系统而言可以极大提高导航定位的可用性、精确性、完好性和可靠性，因此研究多系统组合定位具有重要的意义。不同于GPS卫星导航星座，北斗卫星导航星座是由地球静止轨道卫星(GEO)、倾斜地球同步轨道卫星(IGSO)和地球中轨卫星(MEO)组成。受轨道精度、多路径效应与观测误差特性等影响，GPS、GEO、IGSO、MEO 4类卫星的观测值精度差异较大，若将此4类卫星伪距赋予相同的权比，将导致构造权阵不够准确，降低定位精度^[1]。Helmert方差分量估计法(以下简称Helmert模型)广泛应用于卫星导航定位中不同类型观测值的精确定权，它利用第一次平差的改正数来更新验前方差，降低观测数据异常的权重，从而得到更高精度的定位结果^[2]，但是当卫星数量较少、几何图形强度较差时，将导致估计各类观测值的方差不够准确。

李鹤峰等^[3]基于实测数据验证了多系统组合导航算法的正确性，然而实测的数据量有限，并且随机模型的研究也过于简单。蔡昌盛等^[4]针对GPS/BDS组合导航定权问题提出了滤波平滑与Helmert验后方差估计的融合定权模型，并对定位结果有较大的提高，但将北斗3类卫星观测值精度视为相同，将导致随机模型的估计不够精确。陶庭叶等^[5]在GPS/BDS单历元基线解算过程中采用了验后估计的方法，根据预平差的改正数重新确定来自不同系统、不同类型观测值的随机模型，有效降低各种系统残余误差的影响，但对于卫星数量较少、几何图形强度较差的情况尚未研究。本文针对此类问题，将BDS卫星进行分类研究，提出一种基于GPS、GEO、MEO、IGSO观测值分类定权的指数加权Helmert方差分量估计法(以下简称指数加权Helmert模型)，分别在静态与车载导航的情况下进行实验，并与等权模型、Helmert模型相比较，结果表明，该模型能提高导航定位的精度。

1 GPS/BDS分类组合定位模型

对于GPS/BDS组合单点定位而言，GPS、BDS卫星伪距观测方程表示分别如下^[4]：

$ \begin{array}{l} {P^{{\rm{GPS}}}}{\rm{ = }}{\rho ^{{\rm{GPS}}}} + c{\rm{d}}{t_r} - c{\rm{d}}{T_{{\rm{GPS}}}} + {I_{{\rm{GPS}}}} + {T_{{\rm{GPS}}}} + {\varepsilon _{{\rm{GPS}}}}\\ \;\;\;{P^{{\rm{BDS}}}}{\rm{ = }}{\rho ^{{\rm{BDS}}}} + c{\rm{d}}{t_r} + c{\rm{d}}{t_{{\rm{BDS - GPS}}}} - c{\rm{d}}{T_{{\rm{BDS}}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{I_{^{{\rm{BDS}}}}} + {T_{^{{\rm{BDS}}}}} + {\varepsilon _{^{{\rm{BDS}}}}} \end{array} $

(1)

式中，P为L₁/B₁的伪距观测值；ρ为卫星到接收机的几何距离(消除地球自转影响后)；c为光速(299 792 458 m/s)；dt_r、dT分别为接收机钟差、卫星钟钟差，其中卫星钟钟差采用广播星历计算；dt_BDS－GPS为系统间的时间偏差，作为待估参数进行求解；I为电离层延迟，采用无电离层组合(Iono-Free-LC)进行消除；T为对流层延迟，采用Saastamoinen模型进行改正^[6]；ε为测量噪声。

将观测方程线性化：

$ \mathit{\boldsymbol{v}} = \mathit{\boldsymbol{H\hat x}} - \mathit{\boldsymbol{l}} $

(2)

式中，$\mathit{\boldsymbol{\hat x}}$ =[x_r y_r z_r dt_r dt_BDS－GPS]^T，分别是通过标准单点定位求得的接收机三维坐标、接收机钟差以及系统间的时间偏差；H =[H_GPS H_MEO H_IGSO H_GEO]^T，分别为GPS、MEO、IGSO、GEO 4类卫星几何设计矩阵；l =[l_GPS l_MEO l_IGSO l_GEO]^T为残差项，采用迭代最小二乘得到接收机坐标：

$ {{\mathit{\boldsymbol{\hat x}}}_{i + 1}} = {{\mathit{\boldsymbol{\hat x}}}_i} + {\left( {{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{PH}}} \right)^{ - 1}}{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{Pl}} $

(3)

其中，P为观测值的初始化权阵，通过卫星高度角计算求得^[7]:

$ \mathit{\boldsymbol{P}} = {\rm{diag}}\left( {\sin {{\left( {{E_1}} \right)}^2}\;\;\;\;\sin {{\left( {{E_2}} \right)}^2}\;\;\;\;\sin {{\left( {{E_n}} \right)}^2}\;\;\; \cdots } \right) $

(4)

式中，E_n为第n颗卫星的高度角，迭代的初始值x₀=[0 0 0]，第i次迭代的结果作为第i+1次迭代的初始值，当两次迭代结果的差值$\left| {{{\mathit{\boldsymbol{\hat x}}}_{i + 1}} - {{\mathit{\boldsymbol{\hat x}}}_i}} \right|$ ≤m时迭代结束(m=0.000 1为设定的阈值，|*|为矩阵的求模运算符)，将${{{\mathit{\boldsymbol{\hat x}}}_{i + 1}}}$作为待估参数的最终值。从式(3)可以看出，定位结果受观测值权阵P的影响，不合理的定权将导致定位精度的降低。

2 基于指数加权模型的Helmert方差分量估计方法

不同于GPS导航系统，BDS导航系统由3类不同轨道的卫星组成，不同类别卫星的轨道精度、观测值精度、多路径效应差异较大，对定位结果的影响不一^[1]。本文在此基础上，提出一种基于GPS、GEO、MEO、IGSO观测值分类定权的指数加权Helmert方差分量估计法。

Helmert方差分量估计法近似公式为^[8]：

$ \hat \sigma _{0\;i}^2 = \frac{{\mathit{\boldsymbol{v}}_i^{\rm{T}}{\mathit{\boldsymbol{P}}_i}{\mathit{\boldsymbol{v}}_i}}}{{{n_i} - {\rm{tr}}\left( {{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{N}}_i}} \right)}} $

(5)

式中，i为观测值类型，n_i为第i类卫星的观测个数，v_i为观测值改正数，P_i为观测值初始化权阵，N_i为观测值的系数阵，可以表示为：

$ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{N}}_i} = \mathit{\boldsymbol{H}}_i^{\rm{T}}{\mathit{\boldsymbol{P}}_i}{\mathit{\boldsymbol{H}}_i}\\ \mathit{\boldsymbol{N}} = {\mathit{\boldsymbol{N}}_{{\rm{GPS}}}} + {\mathit{\boldsymbol{N}}_{{\rm{MEO}}}} + {\mathit{\boldsymbol{N}}_{{\rm{IGSO}}}} + {\mathit{\boldsymbol{N}}_{{\rm{GEO}}}} \end{array} $

(6)

根据GPS、MEO、IGSO、GEO 4种观测值的分类，Helmert模型定权步骤如下^[9]：

1) 根据卫星高度角进行验前估计，确定GPS、MEO、IGSO、GEO观测值初始权阵，并初始化各类卫星权阵比例系数λ_GPS=λ_IGSO=λ_MEO=λ_GEO=1。

2) 进行迭代最小二乘平差，待结果收敛后，分别计算v_i^TP_iv_i。

3) 按照式(5)进行第一次方差分量估计，分别得到4类观测值方差分量的第一次估值$\hat \sigma _{0, i}^2$，再依照下式更新权阵：

$ {{\mathit{\boldsymbol{\hat P}}}_i} = {{\hat \lambda }_i}g{\mathit{\boldsymbol{P}}_i} $

(7)

其中，${\hat \lambda _i} = \left( {\hat \sigma _{0,{\rm{GPS}}}^2/\hat \sigma _{0,i}^2} \right)g{\lambda _i}$。

4) 将更新后的权阵不断对步骤2)、3)进行迭代，直到各类观测值的验后方差满足$\hat \sigma _{0,{\rm{GPS}}}^2$ = $\hat \sigma _{0, {\rm{MEO}}}^2$ = $\hat \sigma _{0, {\rm{IGSO}}}^2$ = $\hat \sigma _{0, {\rm{GEO}}}^2$后退出迭代，将收敛后的权比代入式(3)求取最后的结果。当前历元在满足收敛条件后，可以得到GPS卫星与MEO、ISGO、GEO卫星权阵的相对比例系数λ_GPS/i(若某个历元没有此类可见卫星，则λ_GPS/i为0)：

$ \begin{array}{l} {{\hat \lambda }_{{\rm{GPS/MEO}}}}{\rm{ = }}\frac{{{{\hat \lambda }_{{\rm{GPS}}}}}}{{{{\hat \lambda }_{{\rm{MEO}}}}}}, {\lambda _{{\rm{GPS/IGSO}}}} = \frac{{{{\hat \lambda }_{{\rm{GPS}}}}}}{{{{\hat \lambda }_{{\rm{IGSO}}}}}}, \\ \;\;\;\;\;\;\;\;\;\;\;\;{\lambda _{{\rm{GPS/CEO}}}} = \frac{{{{\hat \lambda }_{{\rm{GPS}}}}}}{{{{\hat \lambda }_{{\rm{GEO}}}}}} \end{array} $

(8)

若某个历元由于各类观测卫星数量较少，卫星几何图形强度较差，往往导致得到的权比是不准确的。本文对传统算法进行改进，提出一种基于指数加权衰减记忆滤波应用于GPS、GEO、IGSO、MEO卫星观测值相对权重的计算：

$ \lambda \left( k \right) = \frac{{\sum\limits_{j = k - n + 1}^k {\beta \left( j \right)\lambda \left( j \right)} }}{{\sum\limits_{j = k - n + 1}^k {\beta \left( j \right)} }}\left( {1 \le j \le 10} \right) $

(9)

$ \beta \left( j \right) = \frac{{1 - {e^j}}}{{1 - e}}\left( {1 \le j \le 10} \right) $

(10)

第k个历元的相对权重是结合k－n+1历元到第k个历元滤波平滑后的结果，n为平滑区间的长度(本文通过实验分析选取n=10作为平滑长度)，其中第j个历元的衰减因子β(j)如式(10)所示。若当前历元观测卫星数量较少或卫星数量突然变化时，更新的权比经过滤波算法将对定位结果的影响有限，同时离当前历元越远衰减因子系数越小，也能削弱历史权比对当前定位结果的影响^[10]。

3 实验与分析

为了验证该模型应用于GPS/BDS组合定位的正确性，本文分别进行了静态观测与实测导航实验。

3.1 静态实验分析

静态观测采用2017-01-20 IGS跟踪站点GMSD的GPS+BDS观测数据，接收机类型为TRIMBLE NETR9，截止高度角为15°，采样率为30 s。采用IGS站提供的周解文件的坐标值作为GMSD站参考坐标。

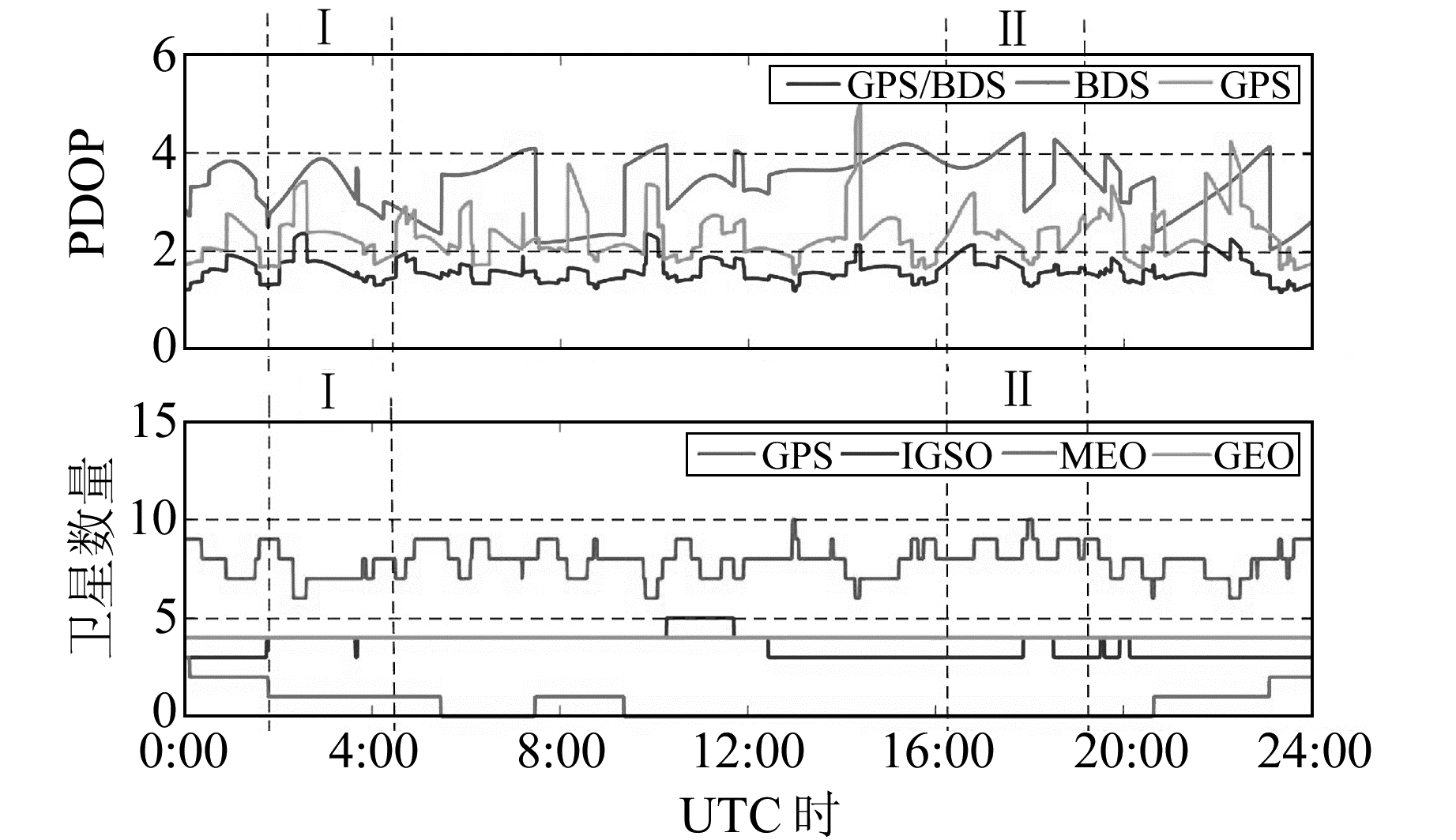
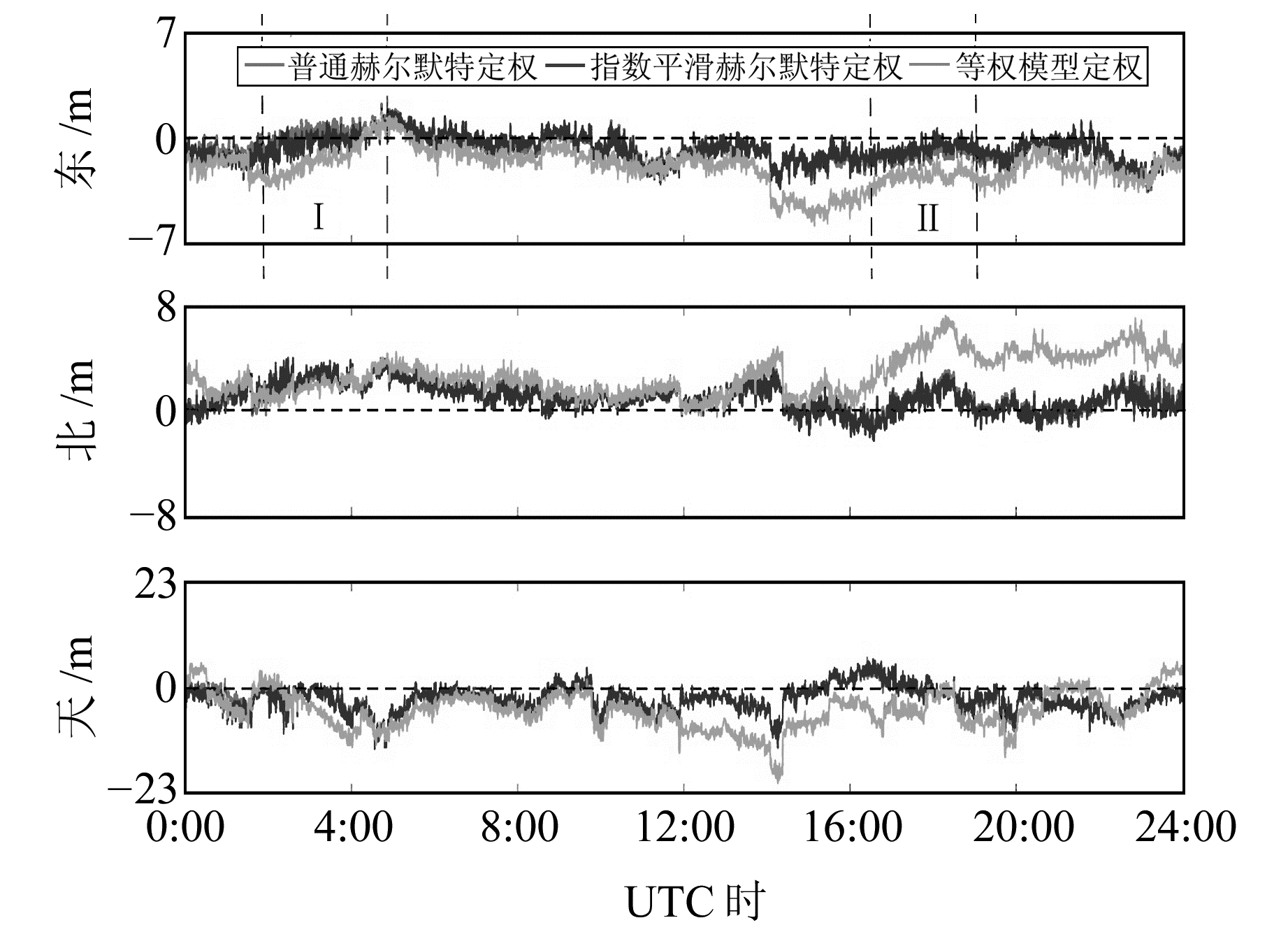
在静态观测实验中，GPS与BDS的3类卫星分别采用等权模型、Helmert模型和指数加权Helmert模型。表 1为不同平滑区间长度下东、北、天3个方向的定位精度结果。可以看出，平滑长度n从1增加到10，定位精度有显著的提高，但随着平滑宽度增加到15时，定位精度的变化较为平缓，且n过大时会造成大量的历史信息进入滤波平滑，可能会导致当前历元的权比不合理^[11-15]，故本文将n=10作为平滑长度应用于指数加权Helmert模型。图 1为当天4类卫星数量的变化和PDOP值。从图 1可知，采用GPS/BDS组合定位，可用卫星数量较单系统增多近一倍，PDOP值明显减小，卫星分布几何图形强度得到了明显改善。图 2为东、北、天3个方向的误差时间序列，可以看出，使用指数加权Helmert模型的定位结果明显优于等权模型，其中在两条虚线指出的Ⅰ、Ⅱ区域中本文的方法较Helmert模型有所提高。

图 3为3种定权方式对GPS与BDS 3类卫星权比的影响。5：00~7：30与9：00~21：00时间段GPS:MEO权比为0，表明该时间段没有观测到MEO卫星。由图 1与图 3对应的虚线Ⅰ、Ⅱ区域可知，当MEO卫星与GPS卫星数量突然减少且观测卫星构成几何图形较差时，将导致固定权与Helmert模型定权不够准确，但采用本文提出的新方法后，定位结果能得到较好的改正。

3.2 动态实验分析

为了测试新的定权模型在动态条件下的有效性，本文进行了实测导航实验，地点为江苏省徐州市中国矿业大学南湖校区，时间为2017-03-22 07：00，卫星截止高度角为15°，采样率为1 s。采用双差载波相位的定位结果作为参考坐标，移动站与基准站配备相同的板卡，基准站架设在环境与测绘学院天台，其坐标通过精密单点定位获取(PPP)，在整个动态观测过程中基线长度小于1 km。

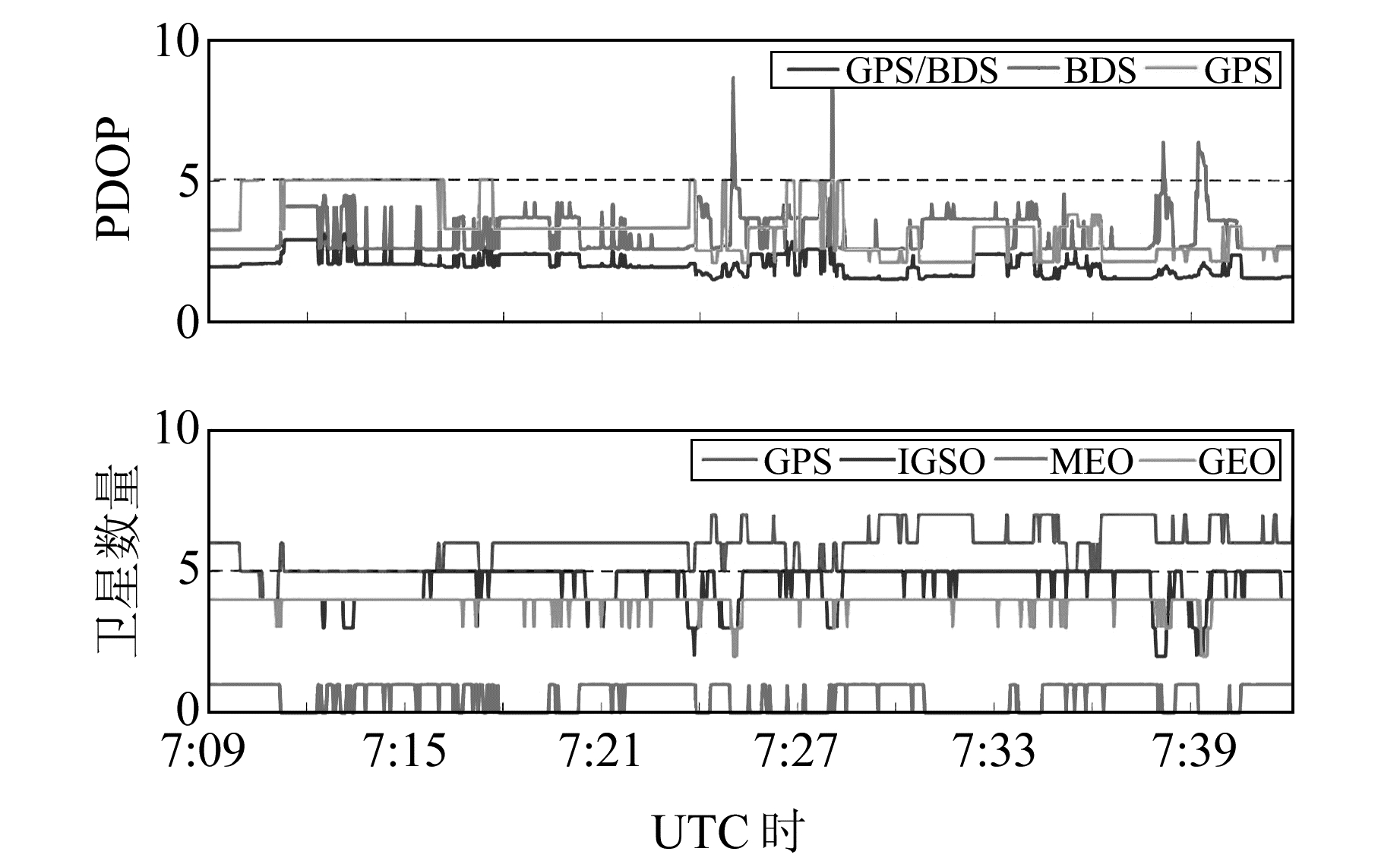
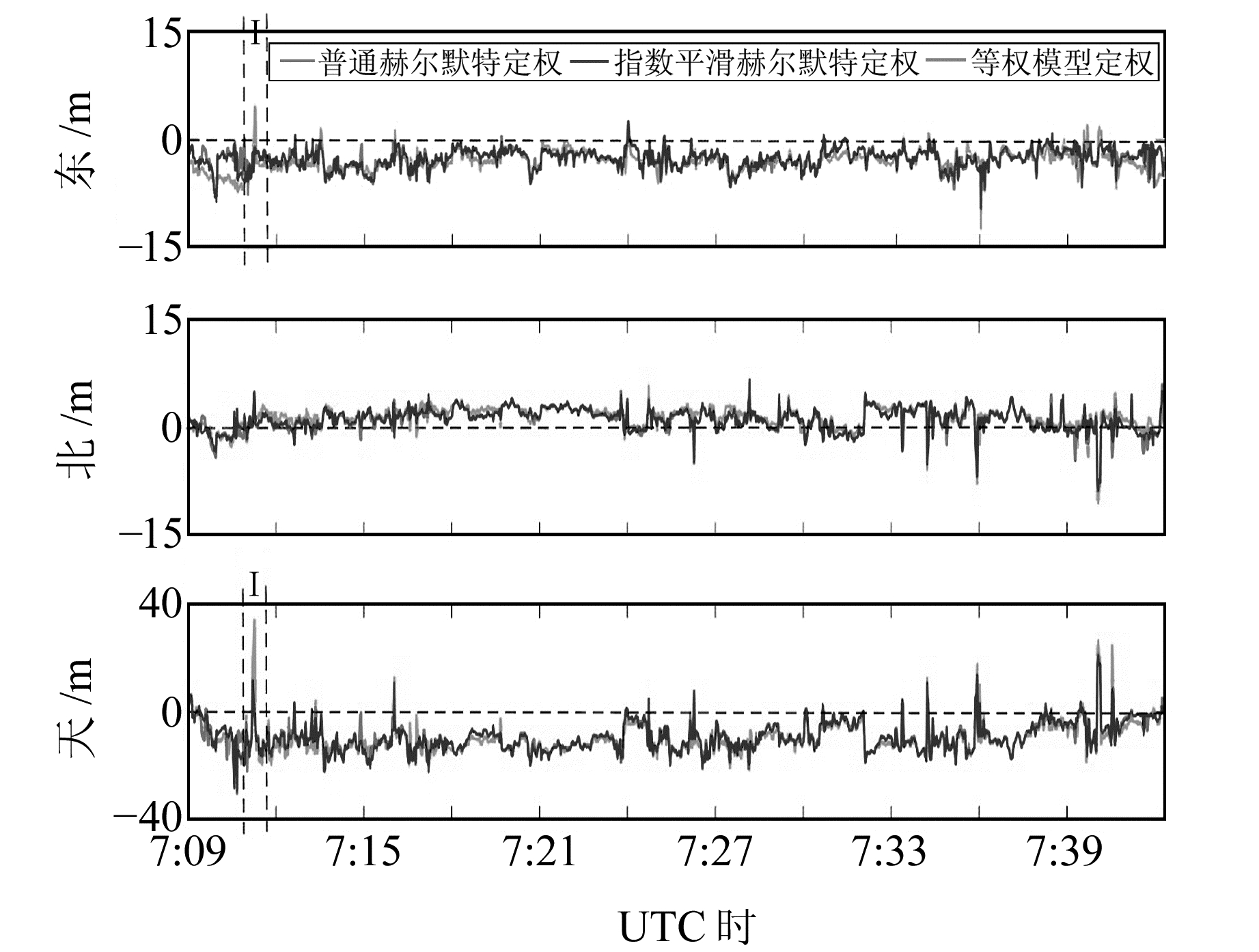
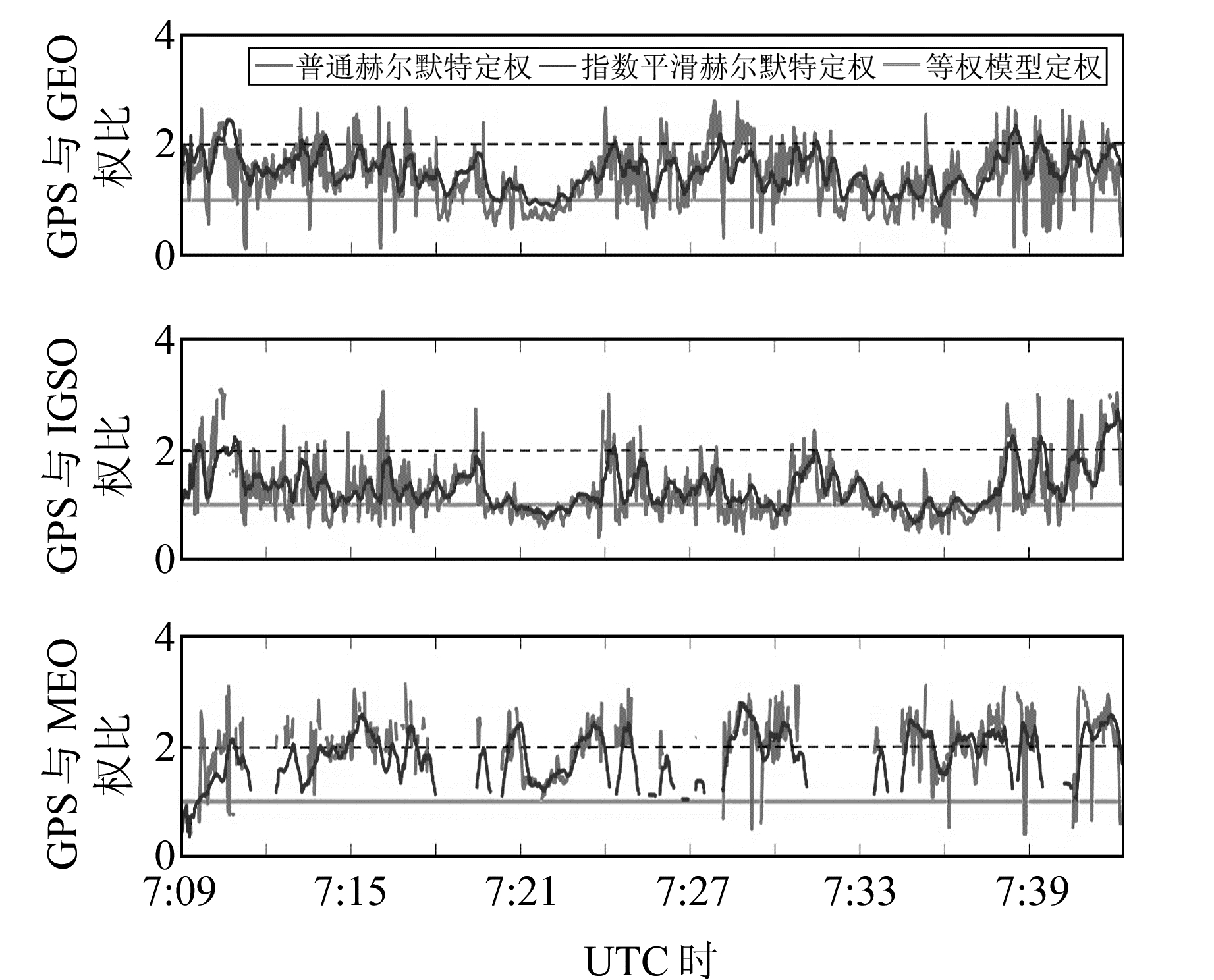
图 4为动态车载实验PDOP值与卫星数量变化图，在30 min的动态实验中，可用卫星数量GPS大约在6颗左右，IGSO、GEO分别为5颗与4颗左右，偶尔能观测到1颗MEO卫星，其PDOP值平均在2.1左右。图 5为动态车载实验3种定权方式对定位结果的误差时间序列图，由图可知，3种定权方式对动态定位结果差别较小，但在可用GPS、IGSO、GEO卫星数量较少的情况(图中虚线Ⅰ区域)下采用本文的定权模型较等权模型有显著的提高。图 6是在车载动态实验中3种定权方式对权比影响的时间序列图，由图可知，本文采用的新的定权模型较Helmert模型更为稳定、平滑。

表 2、表 3分别列出了等权模型、Helmert模型、指数加权Helmert模型在静态与动态车载情况下定位结果的均方根值(RMS)以及指数加权Helmert模型相对于其他两种模型的提高率、最大误差。从表 2可以看出，采用本文的新模型与Helmert模型相比定位结果更加准确，与固定权模型相比有显著的提高，在静态情况下达到了50%的提高率。从表 3可知，静态与动态定位情况下各方向的最大误差相比其他两种定权模型都有所减小，其中与固定权比减小量尤为明显。通过以上分析，进一步验证了指数加权Helmert模型定位结果优于其他两种定权模型，同时也指明了不合理的权阵对定位结果将产生较大影响。

4 结语

不同系统观测值精确的定权对定位精度有着重要的影响，确定合理的权阵是多系统卫星导航的关键。在GPS/BDS单点定位中，本文根据北斗星座构成的特殊性以及各类卫星观测值精度的差异等，将IGSO、GEO、MEO卫星分类研究，并对Helmert模型进行优化，提出了一种依据BDS系统卫星类型以及观测值残差信息的融合定权模型。为了验证该模型在GPS/BDS组合定位中的定位精度优于常规模型，分别在静态与车载动态的条件下进行测试，得到以下结论：

1) 新模型较等权模型在定位精度上有显著的提高，静态条件下东、北、天3个方向的定位精度分别提高50%、51%、42%，动态条件下分别提高10%、8%、9%。

2) 新模型较普通Helmert模型在卫星数量突然减少，且观测卫星构成几何图形较差时定位精度有所提升，对于进一步提升GPS/BDS组合定位精度有一定的参考意义。

本文仅针对GPS/BDS组合进行了分析，对GPS/GLONASS、GLOANSS/BDS等卫星系统的组合有待进一步研究。