北斗卫星导航系统(Beidou navigation satellite system,BDS)是中国自主研发、独立运行的全球卫星导航系统。至2016年年底,我国的第二代北斗卫星导航系统已发射23颗卫星,其中包括在轨工作卫星14颗,在轨测试卫星4颗,主要为亚太地区提供定位导航授时(position navigation time,PNT)服务[1]。实时卫星钟差作为实时应用的核心产品之一,是卫星导航定位系统实现高精度实时PNT服务的前提条件,其可用性和精度直接影响实时服务性能[2-4]。目前部分学者利用MGEX观测网络(the IGS multi-GNSS experiment network)提供的高频观测数据对BDS实时卫星钟差估计算法及性能进行研究,并取得了丰富的成果[5-7]。
在高精度卫星钟差估计过程中,测站应均匀选取[8],同时应有足够的观测数据。但若选取的测站数量过多,解算效率又会降低,且解算精度提高不明显[9]。因此,对于实时钟差产品的求解,在提高测站数的同时也要保障其实时性,从整体上分析最合适的测站数是很有必要的。基于此,本文分析了中国区域内测站数量与BDS实时卫星钟差估计精度的关系,并利用实时精密单点定位(real-time precise point positioning,RTPPP)技术,分析不同测站数量估计的实时钟差对定位精度的影响。
1 实时卫星钟差估计模型实时卫星钟差估计模型目前主要包括非差观测模型和历元间差分模型两种。历元差分模型通过在历元间求差,消除模糊度参数,只保留数量相对较少的卫星钟差、接收机钟差和对流层参数,提高了处理效率,能够有效保证钟差产品的实时性[10-11]。非差模型能够保留模糊度参数,且估计精度较高,但测站较多时处理效能较低[12-13]。考虑到解算BDS区域实时钟差时需要的测站数量较少,一般30个测站就能满足其要求,利用非差模型求解,每个历元的解算时间均在1 s以内,不影响其解算效率,且钟差精度较高。因此,本文采用非差模型实时估计BDS卫星钟差,对应的伪距和相位观测值误差方程为:
| $ \left\{ \begin{array}{l} {\nu _{Pc}} = {\rm{d}}t - {\rm{d}}{t^j} + {M^j}{d_{{\rm{trop}}}} + {D^j} - {\widetilde P^j}\\ {\nu _{Lc}} = {\rm{d}}t - {\rm{d}}{t^j} + {M^j}{d_{{\rm{trop}}}} - {N^j} + {D^j} - {\widetilde L^j} \end{array} \right. $ | (1) |
式中,dt、dtj分别为接收机和卫星钟差参数,dtrop、Mj分别为对流层延迟和映射函数,Nj为无电离层相位组合观测值的模糊度,Dj为卫星到测站间的几何距离,
在实时卫星钟差估计中,实时数据预处理是获得高精度钟差值的保障。然而,数据预处理后仍可能有残余粗差存在,而且噪声较大的观测数据也难以在预处理阶段被完全消除,从而制约了实时卫星钟差解算精度。因此,本文采用残差控制策略对观测数据质量进一步控制,根据观测值的后验残差控制观测数据,提高实时卫星钟差的可靠性。同时匹配广播星历钟差值进行实时卫星钟差修正值计算,将实时钟差产品基准统一到广播钟差基准上。
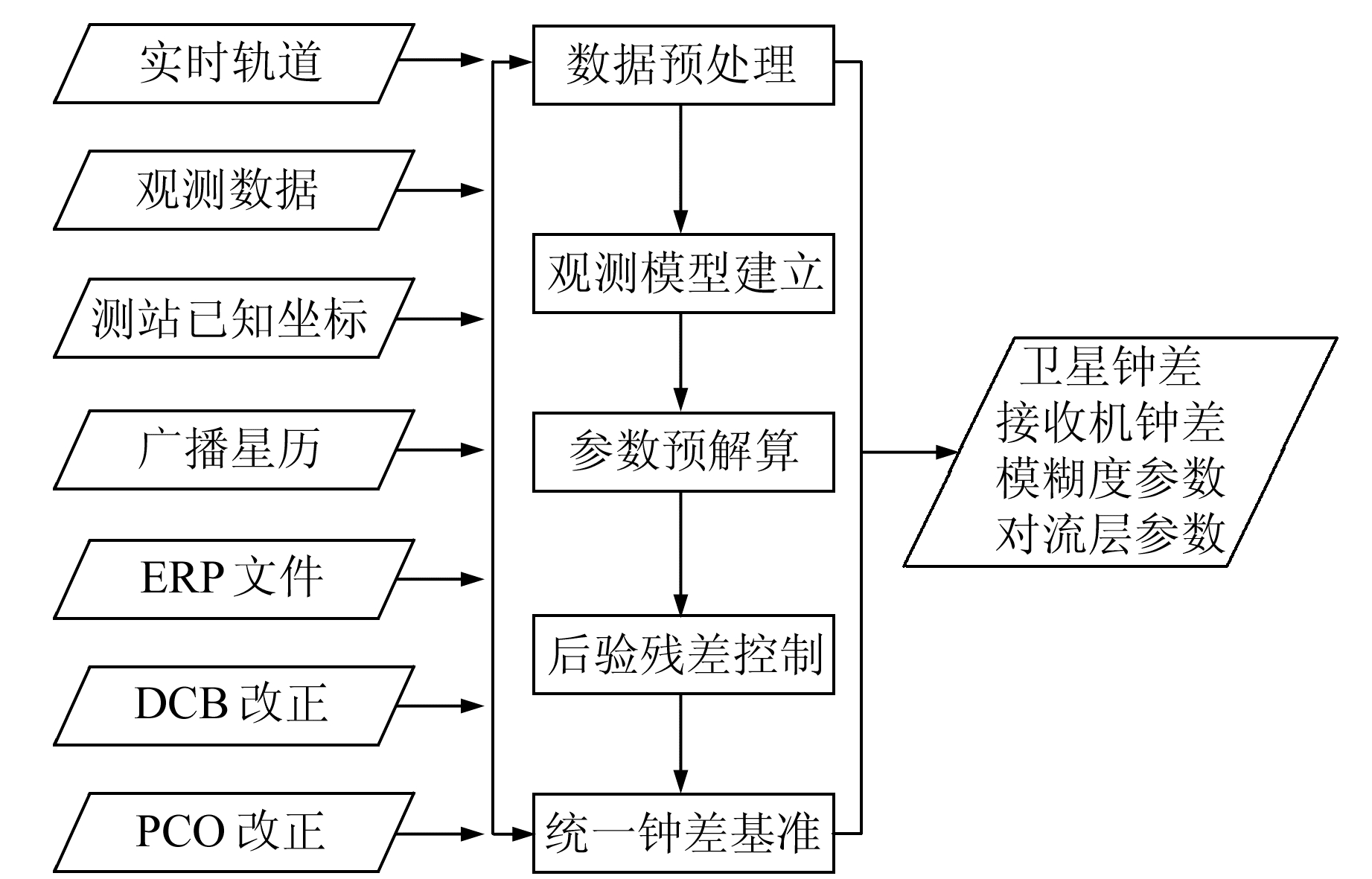
本文的数据处理流程如图 1所示。图 1中,左边是输入的数据,包括观测数据、实时轨道、测站已知坐标、广播星历、地球自转参数(earth rotation parameter, ERP)文件、码偏差(differential code bias, DCB)改正和天线相位中心(phase center offset, PCO)改正等;中间是实时钟差解算的处理流程;右边是输出的产品结果。
|
图 1 实时钟差解算处理流程 Fig. 1 Flowchart of real-time clock estimation |
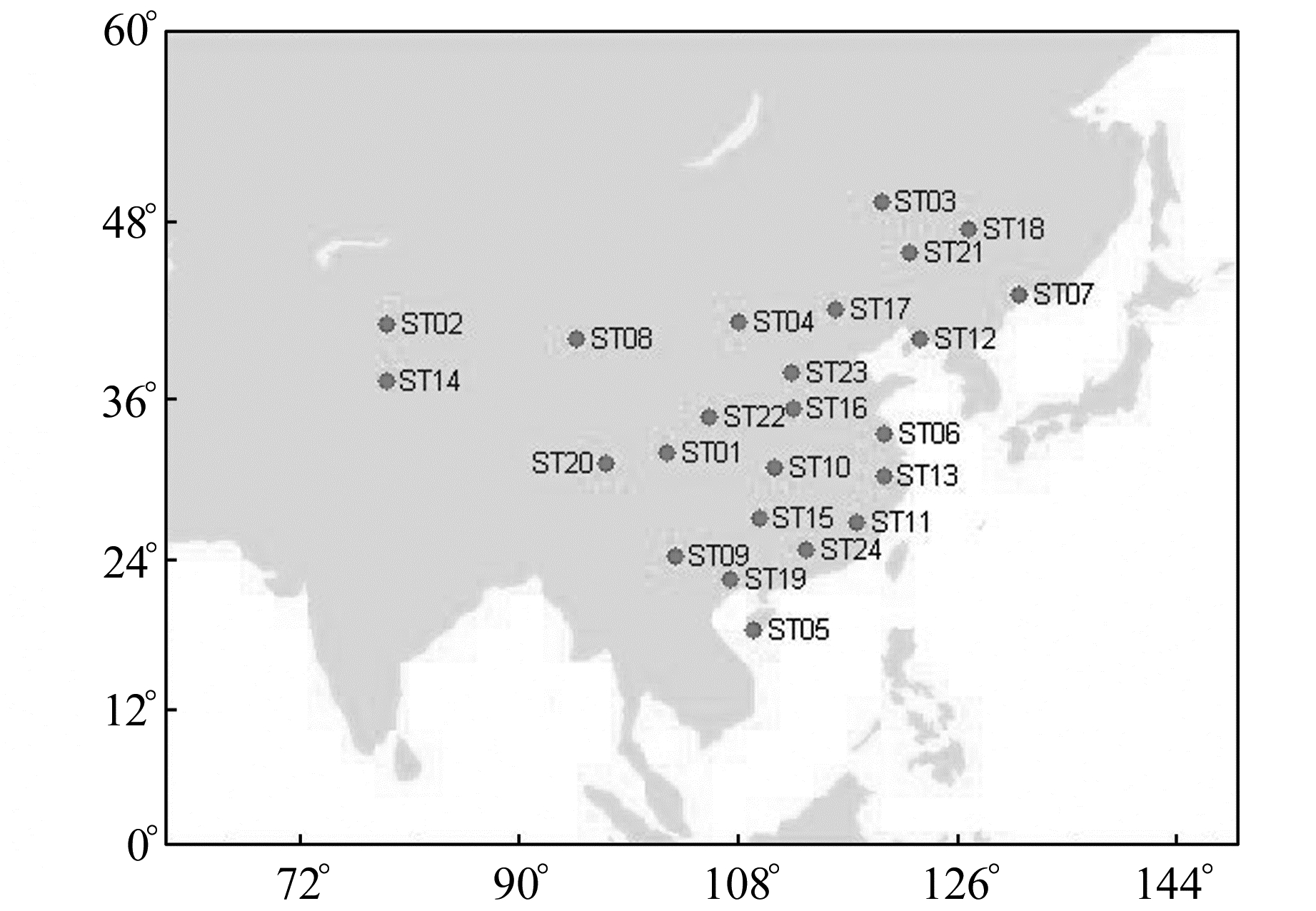
为了分析区域测站数与BDS实时钟差估计精度的关系,采用长安大学北斗分析中心提供的实时轨道产品,其GEO卫星轨道精度优于2 m,IGSO/MEO卫星轨道精度优于10 cm。利用中国区域内均匀选取的24个实时监测站2016-11-08~14连续7 d的实时观测数据,分析了从8 ~ 24个不同测站数量的4种测站分布,包括8个、12个、18个、24个(图 2),其实时监测站分别对应测站st01~08、测站st01~12、测站st01~18、测站st01~24。另外,为了进一步分析不同测站数估计的实时钟差对定位精度的影响,采用4种测站数获得的实时钟差值对6个区域测站进行定位解算,统计其定位精度。
|
图 2 实时钟差解算的测站分布 Fig. 2 Distribution of station used for real-time clock estimation |
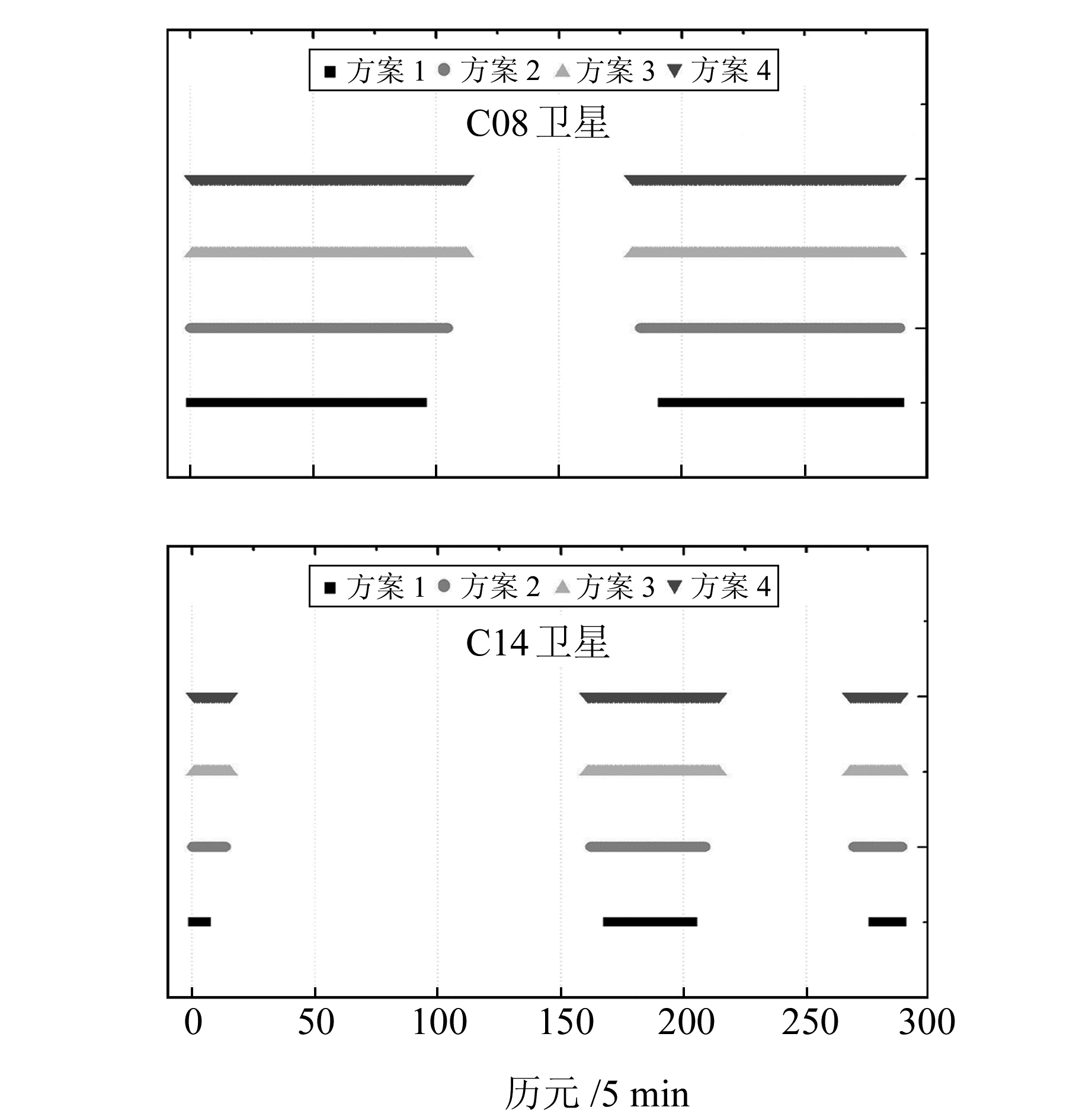
我国的北斗系统属于异质星座结构,3种类型(GEO、IGSO和MEO)卫星由于运行轨道不同呈现观测不均匀的特征。对于GEO卫星,其始终在中国区域上空,参与钟差解算的测站可以全弧长观测,实时估计的钟差序列连续;而IGSO/MEO卫星在中国区域内不能全弧长观测,实时估计的钟差序列呈现多弧段特征。为了更好地显示可观测弧长的差异性,从获得的1 s高频实时钟差中提取出5 min间隔的钟差产品,其中以C08(IGSO)、C14(MEO)卫星为例,统计4种测站数量下获得的IGSO/MEO有效钟差序列如图 3所示,其余几颗卫星的有效钟差序列对应相似。为了更简洁、方便地分析说明问题,4种测站分布依次对应方案1、方案2、方案3和方案4。
|
图 3 C08、C14卫星的有效钟差分布 Fig. 3 Distribution of effective clock for C06, C08 and C14 satellites |
从图 3可以看出,中国区域内IGSO/MEO卫星1 d中(00:00~24:00)能观测的弧长并不连续。对比方案1~3的结果,随着测站数量增多,可观测弧长逐渐增大;对比方案3和方案4的结果,测站数量虽在增多,可观测弧长不再变化。结合4种方案下有效钟差序列的变化趋势可得,方案3采用的测站数可以全部覆盖BDS卫星在中国区域内被观测的弧长。为了进一步细化论证,以C06、C08、C14卫星为例,统计测站数量从12依次增加至18个获得的有效钟差序列占中国区域内可被观测的最大弧长百分比(表 1,单位%),其余几颗卫星有效钟差序列也对应相似。结果显示,当测站数达到16个时,有效钟差产品可观测弧长覆盖饱和。
|
|
表 1 不同测站获得的有效钟差弧长占全部弧长的比例 Tab. 1 The effective arcs obtained by different stations account for the total arc length ratio |
本文采用“二次差”方法评定实时钟差精度。为了避免参考星钟差出现大的偏差时影响评估结果,采用当前历元所有卫星的实时估计钟差与最终钟差产品的差值取平均作为基准偏差值,将此值从各个卫星的钟差差值中扣除。具体公式为:
| $ {x_i} = \sum\limits_{i = 1}^{{m_i}} {\left( {t_i^s - t_{0i}^s} \right)} /{m_i} $ | (2) |
| $ \mathit{\Delta }_i^s = t_i^s - t_{0i}^s - {x_i} $ | (3) |
| $ {\rm{STD = }}\sqrt {\sum\limits_{i = 1}^n {{{\left( {\mathit{\Delta }_i^s - {{\mathit{\overline \Delta } }^s}} \right)}^2}/n} } $ | (4) |
式中,tis、t0is分别是第i历元s号卫星的实时估计钟差和事后精密钟差,xi表示该历元m颗卫星的钟差差值取平均得到的基准偏差值,Δis表示消除基准偏差值的钟差差值,n表示1 d的历元总数。
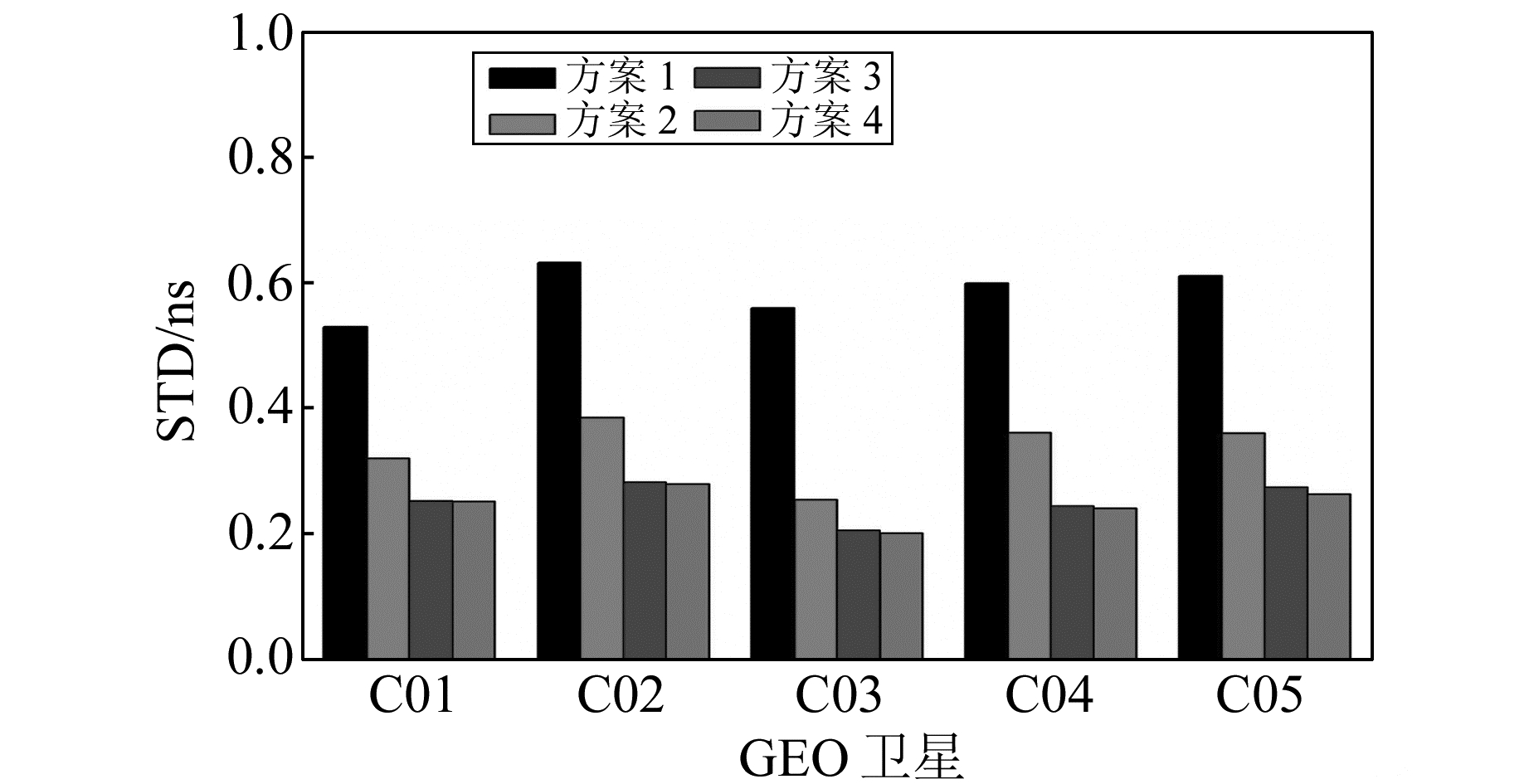
钟差精度评估时以长安大学最终精密钟差产品为参考,其钟差标称精度为0.2 ns。由图 3可知,4种方案下IGSO/MEO卫星的有效实时钟差弧长不同,为了更好地对比不同方案获得的实时钟差性能,GEO卫星统计收敛后连续1 d的实时钟差精度,IGSO/MEO卫星统计收敛后4种方案下相同且连续5 h的实时钟差精度。将7 d的实时钟差精度求平均值,得到4种方案下GEO卫星和IGSO/MEO卫星的实时钟差精度分别如图 4和5所示。
|
图 4 GEO卫星的实时钟差精度 Fig. 4 Accuracy of real-time GEO satellites clock |
|
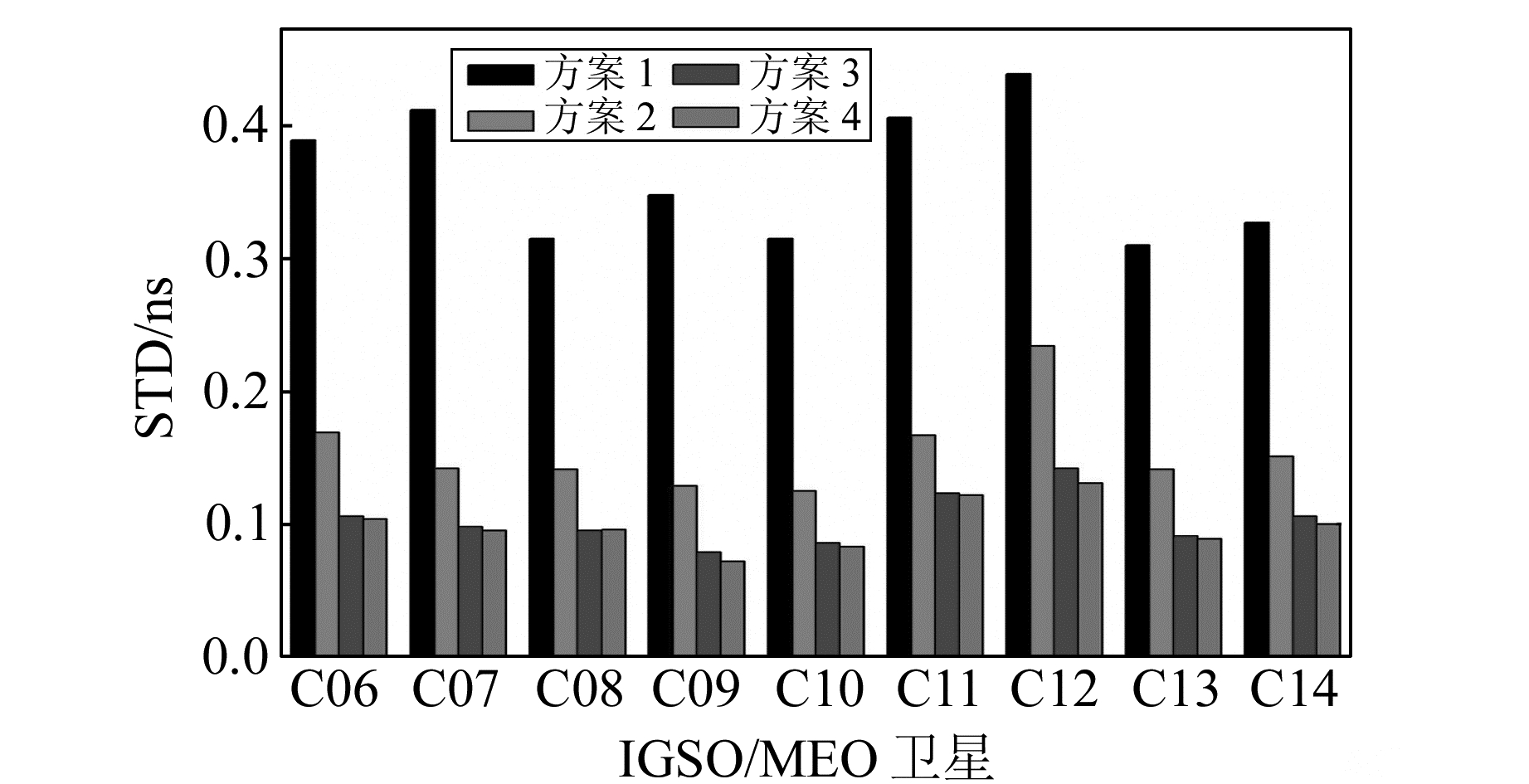
图 5 IGSO/MEO卫星的实时钟差精度 Fig. 5 Accuracy of real-time IGSO/MEO satellites clock |
从图 4和图 5中可以看出,从方案1到方案3,BDS实时钟差精度均在逐渐提高,且从方案1到方案2,钟差精度提升较为明显;从方案3到方案4,BDS实时钟差精度提高不明显。结合方案1到方案3的实时钟差精度变化规律可得,当参与解算的测站数达到方案3使用的测站数时,基本可以估计出中国区域内较高精度的BDS实时钟差;继续增加测站数,实时钟差精度提高不显著。这是因为当测站数据冗余度达到近似饱和时,继续增加观测数据不再能明显提高钟差求解精度。将7 d的实时钟差精度求平均值,得到4种方案下BDS实时卫星钟差的平均估计精度如表 2(单位ns)所示。
|
|
表 2 实时BDS卫星钟差估计的平均精度 Tab. 2 Average accuracy of real-time BDS clock offsets |
从表 2可以看出,方案1获得的实时钟差精度为0.442 ns,随着参与实时钟差解算的测站数目增多,实时钟差精度也会提高,从方案2到方案4,获得的实时钟差与前一方案结果相比,钟差精度分别提高103.8%、39.7%、2.6%。从结果可以看出,随着测站数目增多,钟差精度提升速率在逐渐减小,当测站数目达到方案3时,钟差精度相对较高,达到0.15 ns左右;继续增加测站数,钟差精度提升不再明显,方案4的钟差结果与方案3相比,钟差精度提高仅为0.004 ns,基本相当。为了进一步细化论证,还统计了测站数从16依次增加至18时获得的实时钟差精度,结果如表 3所示。结果显示,当测站数达到17个时,钟差精度已经相对较高,相比18个测站获得的实时钟差值,钟差精度基本相当。
|
|
表 3 实时BDS卫星钟差估计的平均精度 Tab. 3 Average accuracy of real-time BDS clock offsets |
为了进一步分析不同测站数目估计的实时钟差对定位精度的影响,采用8个、12个、17个和24个实时监测站解算出的实时卫星钟差值,对3个参与实时钟差解算的测站和3个未参与实时钟差解算的中国区域测站数据进行实时PPP定位解算,同时采用广播星历对这6个测站进行了定位解算,对比分析广播星历和实时产品的定位精度。因为在§3.3论证中采用17个测站获得的实时钟差精度已经相对较高,故方案3改为对应采用17个实时地面监测站解算实时钟差。将7 d的实时PPP定位精度求平均值,统计了各个测站收敛后E、N、U 3个方向上的定位精度如图 6所示。
|
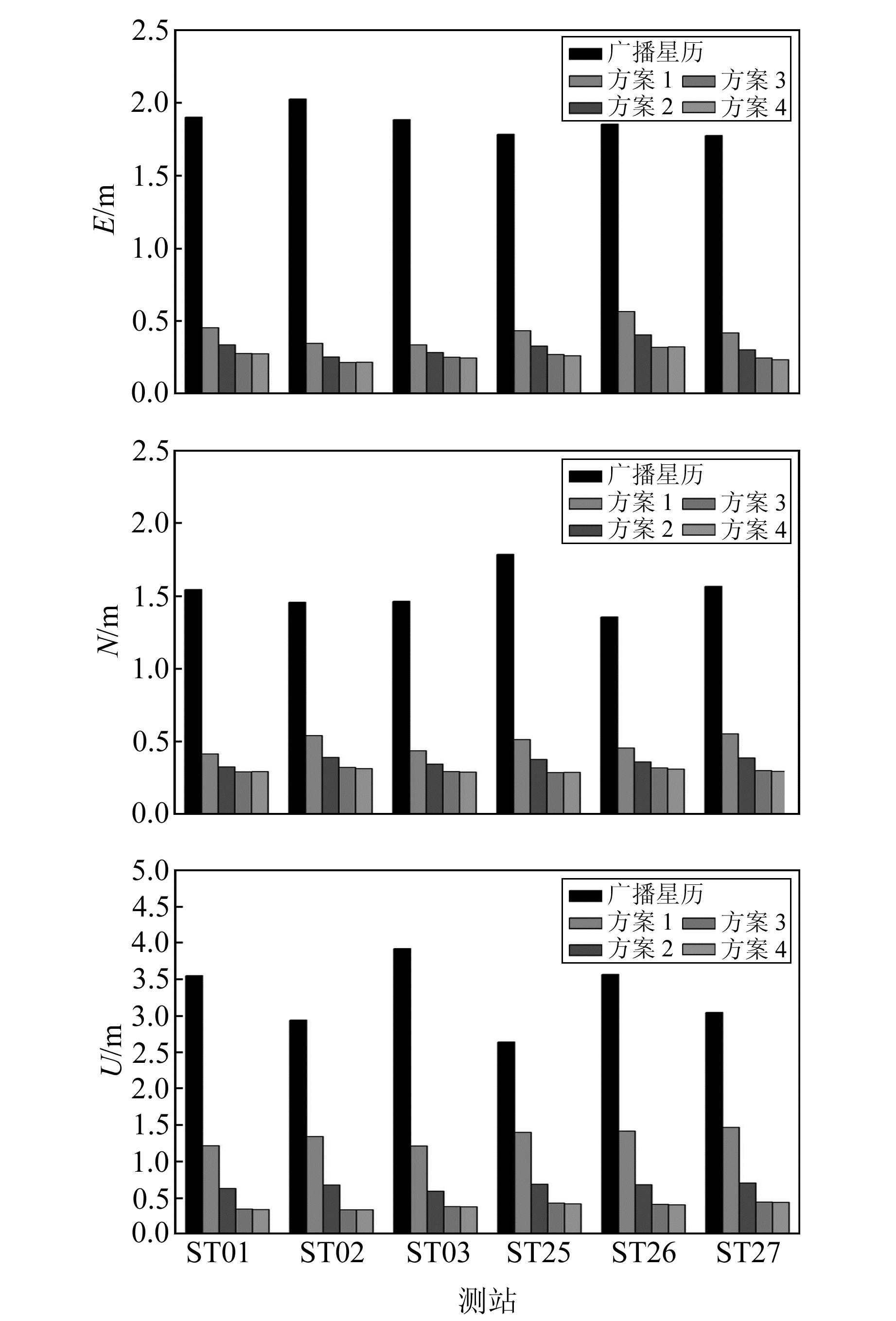
图 6 6个测站的RTPPP定位精度 Fig. 6 Positioning accuracy of RTPPP at 6 stations |
从图 6可以看出,采用方案1~3获得的实时钟差值,RTPPP的定位精度逐渐提高,并且参与钟差解算的测站定位精度略高于没有参与钟差解算的测站,尤其是在高程方向。采用方案4获得的实时钟差值,与采用方案3结果相比,RTPPP的定位精度没有明显提升,说明采用方案3估计出的BDS实时钟差进行RTPPP定位解算,能得到较高的定位精度;继续增加测站数,定位精度提高不显著。这是因为当测站数达到方案3时,钟差精度相对较高,和方案4的钟差结果基本相当,导致定位精度也不再显著提高。另外,采用实时产品进行定位解算与采用广播星历相比,定位精度得到明显提升,在E、N、U方向大约提高了5~10倍。不同测站的平面和高程方向定位精度如表 4(单位m)所示。
|
|
表 4 不同测站平面和高程上的定位精度 Tab. 4 Positioning accuracy at 2D and elevation of the different stations |
从表 4可以看出,方案1的定位精度在平面和高程方向为0.544 m和1.339 m,随着参与实时钟差解算的测站数目增多,获得的实时钟差在定位性能上也会逐渐提高,方案2到方案4的定位结果与前一方案结果相比,平面定位精度分别提高61.9%、31.6%、1.5%,高程定位精度分别提高103.8%、54.3%、1.6%。可以看出,随着测站数目增多,其定位精度提高速率在逐渐减小,当测站数达到方案3时,定位精度相对较高,平面定位精度达到0.3 m以内,高程定位精度达到0.4 m以内;继续增加测站数,定位精度提升不再明显,方案4的定位结果与方案3相比,平面和高程方向的定位精度提高仅为0.004 m和0.006 m,二者基本相当。对比实时产品和广播星历的定位结果可以看出,采用实时产品进行导航定位与广播星历相比,定位精度在平面方向提高了接近5倍,在高程方向提高了接近10倍,大大提升了导航定位的服务能力。
4 结语本文基于非差模型的实时钟差解算策略,实现了BDS实时卫星钟差估计,采用中国区域内均匀选取的8~24个实时地面监测站数据和长安大学北斗分析中心提供的实时BDS轨道产品,分析了中国区域测站数与BDS实时钟差估计精度的关系,并对不同测站数目下获得的实时钟差进行实时PPP定位解算。分析总结如下:在中国区域内,IGSO/MEO卫星1 d中(00:00~24:00)能观测的弧长不连续,当测站数小于16个,其在中国区域内被观测的弧长不全,实时钟差精度和定位精度较差;当测站数达到16个,中国区域内可观测的BDS卫星弧长覆盖饱和;当测站数达到17个及以上,实时钟差精度达到0.15 ns,平面定位精度达到0.3 m以内,高程定位精度达到0.4 m以内,且钟差和定位精度随着测站数的增加不再明显提高。
本文目前从数值角度解析对比了测站数目与BDS实时钟差估计精度的影响关系,为了从理论上揭示测站分布对实时钟差解算的影响,下一步将探究二者之间的几何相关性模型。
致谢 感谢iGMAS分析中心提供实时监测站数据。
| [1] |
杨元喜, 李金龙, 王爱兵, 等. 北斗区域卫星导航系统基本导航定位性能初步评估[J]. 中国科学:地球科学, 2014, 44(1): 72-81 (Yang Yuanxi, Li Jinlong, Wang Aibing, et al. Preliminary Assessment of the Navigation and Positioning Performance of Beidou Regional Navigation Satellite System[J]. Science China: Earth Sciences, 2014, 44(1): 72-81)
(  0) 0) |
| [2] |
Zumberge J F, Heflin M B, Jefferson D C, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research, 1997, 102(B3): 5005-5017 DOI:10.1029/96JB03860
(  0) 0) |
| [3] |
Mohamed E, Salim A. Performance of Real-Time PrecisePoint Positioning Using IGS Real-Time Service[J]. GPS Solut, 2016, 20: 565 DOI:10.1007/s10291-015-0467-z
(  0) 0) |
| [4] |
Hadas T, Bosy J. IGS RTS Precise Orbits and Clocks Verification and Quality Degradation Over Time[J]. GPS Solut, 2015, 19: 93-105 DOI:10.1007/s10291-014-0369-5
(  0) 0) |
| [5] |
Fu W J, Zhang Q. Performance Analysis of Real-Time BDS Clock Estimation with Different Orbit Accuracy[C]. China Satellite Navigation Conference (CSNC), Changsha, 2016
(  0) 0) |
| [6] |
赵齐乐, 戴志强, 王广兴, 等. 利用非差观测量估计北斗卫星实时精密钟差[J]. 武汉大学学报:信息科学版, 2016, 41(5): 686-691 (Zhao Qile, Dai Zhiqiang, Wang Guangxing, et al. Real-Time Precise BDS Clock Estimation with the Unidifferenced Observation[J]. Geomatics and Information Science of Wuhan University, 2016, 41(5): 686-691)
(  0) 0) |
| [7] |
陈良, 耿长江, 周泉. 北斗/GPS实时精密卫星钟差融合解算模型及精度分析[J]. 测绘学报, 2016, 45(9): 1028-1034 (Chen Liang, Geng Changjiang, Zhou Quan, et al. Estimation Model and Accuracy Analysis of Beidou/GPS Real-Time Precise Satellite Clock Error Integrated Resolving[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(9): 1028-1034 DOI:10.11947/j.AGCS.2016.20150296)
(  0) 0) |
| [8] |
楼益栋, 戴小蕾, 宋伟伟. 站间距对GPS卫星高精度钟差估计的影响分析[J]. 武汉大学学报:信息科学版, 2011, 36(4): 397-400 (Lou Yidong, Dai Xiaolei, Song Weiwei, et al. Research on the Influence of Stations'Distance in High-Accuracy GPS Satellite Clock Offset Estimation[J]. Geomatics and Information Science of Wuhan University, 2011, 36(4): 397-400)
(  0) 0) |
| [9] |
杨志军. 卫星精密钟差实时估计方法研究[D]. 成都: 西南交通大学, 2012 (Yang Zhijun. Reseach on the Estimation Methods of Real-Time Precise Satellite Clock Bias[D]. Chengdu: Southwest Jiaotong University, 2012) http://cdmd.cnki.com.cn/Article/CDMD-10613-1015338340.htm
(  0) 0) |
| [10] |
Ge M R, Chen J P, Douša J, et al. A Computationally Efficient Approach for Estimating High-Rate Satellite Clock Corrections in Realtime[J]. GPS Solut, 2009, 16: 9-17
(  0) 0) |
| [11] |
Zhang X H, Li X X, Guo F. Satellite Clock Estimation at 1Hz for Realtime Kinematic PPP Applications[J]. GPS Solut, 2011, 15: 315-324 DOI:10.1007/s10291-010-0191-7
(  0) 0) |
| [12] |
楼益栋, 施闯, 周小青, 等. GPS精密卫星钟差估计与分析[J]. 武汉大学学报:信息科学版, 2009, 34(1): 88-91 (Lou Yidong, Shi Chuang, Zhou Xiaoqing, et al. Realization and Analysis of GPS Precise Clock Products[J]. Geomatics and Information Science of Wuhan University, 2009, 34(1): 88-91)
(  0) 0) |
| [13] |
李星星, 徐运, 王磊. 非差导航卫星实时/事后精密钟差估计[J]. 武汉大学学报:信息科学版, 2010, 35(6): 661-664 (Li Xingxing, Xu Yun, Wang Lei. Undifferenced Precise Satellite Clock Error Estimation and Precision Analysis[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6): 661-664)
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38


