2. 武汉大学地球空间环境与大地测量教育部重点实验室,武汉市珞喻路129号,430079;
3. 内蒙古自治区航空遥感测绘院,呼和浩特市兴安南路42号,010051
目前对BDS短基线解算的研究较多[1-2],主要体现在数据处理模型、多频线性组合和模糊度解算等方面[3-4]。对中长基线解算的研究相对较少,特别是利用实测数据对BDS中长基线实际动态定位性能的评估与分析更少。祝会忠等[5]提出一种BDS网络RTK中距离参考站整周模糊度的单历元解算算法,并利用CORS网实测数据对算法进行验证。刘鸣等[6]提出一种BDS中长基线基准站间整周模糊度快速确定方法,并给出该方法的数学模型、方法步骤和数据检验结果。但这些都是多基站的中长基线动态定位,没有对单基站的定位性能进行详细分析。在工程实践中,BDS中长基线动态定位能够达到什么样的定位精度,以及利用单BDS观测数据能够在多长时间内实现稳定可靠的精密定位是用户最为关心的问题,但目前鲜见公开报道。因此,本文主要开展BDS系统中长基线动态定位的实际性能研究,重点分析模糊度首次固定时间(time to first fix, TTFF)和定位精度,以期为BDS系统的实际应用提供参考。
1 BDS中长基线动态定位算法 1.1 中长基线动态定位的数学模型和误差源在单基线模式下,BDS伪距观测值和载波相位观测值的双差观测方程为[7]:
| $ \mathit{\Delta }\;\nabla P_{b, r}^{i, j} = \mathit{\Delta }\;\nabla \rho _{b, r}^{i, j} + \mathit{\Delta }\;\nabla I_{b, r}^{i, j} + \mathit{\Delta }\;\nabla T_{b, r}^{i, j} + {\varepsilon _P} $ | (1) |
| $ \begin{array}{l} {\rm{ \mathit{ λ} }}\mathit{\Delta }\;\nabla \varphi _{b, r}^{i, j} = \mathit{\Delta }\;\nabla \rho _{b, r}^{i, j} - \mathit{\Delta }\;\nabla I_{b, r}^{i, j} + \mathit{\Delta }\;\nabla T_{b, r}^{i, j} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ \mathit{ λ} }}\mathit{\Delta }\;\nabla N_{b, r}^{i, j} + {\varepsilon _\varphi } \end{array} $ | (2) |
式中,
经双差之后,接收机和卫星的钟差、硬件延迟偏差均可消除,电离层延迟误差和对流层延迟误差可以得到不同程度的削弱。卫星轨道误差对定位的影响可简单地用以下公式估计[7]:
| $ \Delta b = \alpha \times \frac{{{\Delta _{{\rm{orb}}}}}}{\rho } \times b $ | (3) |
式中,Δb为卫星轨道对基线长的影响;Δorb为卫星轨道三维精度;ρ和b分别为卫地距和基线长;α为影响因子,一般取0.1~0.25。根据目前北斗广播轨道的精度[8],对于100 km的中长基线,轨道误差对基线长的影响小于5.6 mm,可以忽略。对于中长基线(通常认为中长基线为10~100 km),大气误差的空间相关性减弱,双差后的大气残余误差仍然很大,影响模糊度浮点解的精度,增大了模糊度固定的难度,不能将其忽略。下面重点介绍在BDS中长基线处理中,电离层延迟误差和对流层延迟误差的处理方法和策略。
1.2 中长基线电离层误差处理电离层延迟误差有两种处理方法,一种是利用双频消电离层组合,另一种是对其进行估计。本文使用消电离层算法,其双差观测方程为:
| $ \begin{array}{l} \mathit{\Delta }\;\nabla {\rm{I}}{{\rm{F}}_p} = f_1^2/\left( {f_1^2 - f_2^2} \right) \times \mathit{\Delta }\;\nabla {P_1} - \\ \;\;\;\;\;\;\;\;\;\;f_2^2/\left( {f_1^2 - f_2^2} \right) \times \mathit{\Delta }\;\nabla {P_2} \end{array} $ | (4) |
| $ \begin{array}{l} \mathit{\Delta }\;\nabla {\rm{I}}{{\rm{F}}_\mathit{\Phi }} = f_1^2/\left( {f_1^2 - f_2^2} \right) \times {{\rm{ \mathit{ λ} }}_1}\mathit{\Delta }\;\nabla {\varphi _1} - \\ \;\;\;\;\;\;\;\;\;\;f_2^2/\left( {f_1^2 - f_2^2} \right) \times {{\rm{ \mathit{ λ} }}_2}\mathit{\Delta }\;\nabla {\varphi _2} \end{array} $ | (5) |
由于消电离层组合的模糊度不具有整数特性,不能将其固定为整数,将式(5)作如下变换:
| $ \begin{array}{l} \mathit{\Delta }\;\nabla {\rm{I}}{{\rm{F}}_\mathit{\Phi }} = f_1^2/\left( {f_1^2 - f_2^2} \right) \times {\lambda _1}\mathit{\Delta }\;\nabla {\varphi _1} - \\ \;\;\;\;\;\;f_2^2/\left( {f_1^2 - f_2^2} \right) \times {\lambda _2}\mathit{\Delta }\;\nabla {\varphi _2}{\rm{ = }}\\ \;\;\;\;\;\;\mathit{\Delta }\;\nabla \rho + \mathit{\Delta }\;\nabla T + \left( {f_1^2{\lambda _1}\mathit{\Delta }\;\nabla {N_1} - } \right.\\ \;\;\;\;\;\;\left. {f_2^2{\lambda _2}\mathit{\Delta }\;\nabla {N_2}} \right)/\left( {f_1^2 - f_2^2} \right) + {{\varepsilon '}_\varphi } = \\ \mathit{\Delta }\;\nabla \rho {\rm{ + }}\mathit{\Delta }\;\nabla T + \left( {f_1^2} \right.{\lambda _1} \times \left( {\mathit{\Delta }\;\nabla } \right.{N_1} - \\ \;\;\;\;\;\;\left. {\mathit{\Delta }\;\nabla {N_2}} \right) + \left( {f_1^2{\lambda _1} - f_2^2{\lambda _2}} \right) \times \\ \;\;\;\;\;\;\left. {\mathit{\Delta }\;\nabla {N_2}} \right) + \left( {f_1^2 - f_2^2} \right) + {{\varepsilon '}_\varphi }{\rm{ = }}\\ \mathit{\Delta }\;\nabla \rho {\rm{ + }}\mathit{\Delta }\;\nabla T + f_1^2{\lambda _1}\mathit{\Delta }\;\nabla {N_5}/\left( {f_1^2 - f_2^2} \right){\rm{ + }}\\ \;\;\;\;\;\;\;\;\;\;\;\;c\mathit{\Delta }\;\nabla {N_2}/\left( {{f_1} + {f_2}} \right) + {{\varepsilon '}_\varphi } \end{array} $ | (6) |
| $ \begin{array}{l} \mathit{\Delta }\;\nabla {N_5} = \mathit{\Delta }\;\nabla {N_{\left( {1, - 1, 0} \right)}} = \mathit{\Delta }\;\nabla {N_{\left( {1, 4, - 5} \right)}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;5\mathit{\Delta }\;\nabla {N_{\left( {0, - 1, 1} \right)}} \end{array} $ | (7) |
可以看出,消电离层组合观测值的模糊度可以分解为宽巷模糊度Δ▽N5和窄巷模糊度的组合。宽巷模糊度具有较长的波长,更容易固定。对于三频观测数据,通常先固定超宽巷模糊度(0, -1, 1)和(1, 4, -5),然后按照式(7)计算宽巷模糊度Δ▽N5。利用固定的宽巷模糊度求解窄巷模糊度的浮点解,并进行固定,最后利用窄巷固定解,可求取高精度的基线分量。
1.3 中长基线对流层误差处理对流层延迟分为干延迟和湿延迟两个部分,干延迟(约占总延迟量的90%)可以利用现有模型进行很好的改正,湿延迟(约占总延迟量的10%)则很难利用模型进行精确改正。本文将中长基线中对流层湿延迟部分作为待估参数进行求解。
| $ \begin{array}{l} \;\;\;\;\;\;\mathit{\Delta }\;\nabla T_{b, r}^{i, j}{\rm{ = }}\mathit{\Delta }\;\nabla T_{b, r}^j - \mathit{\Delta }\;\nabla T_{b, r}^i = \\ \left( {{\rm{MF}}_r^j{T_r} - {\rm{MF}}_b^j{T_b}} \right) - \left( {{\rm{MF}}_r^i{T_r} - {\rm{MF}}_b^i{T_b}} \right) \end{array} $ | (8) |
式中,Tr、Tb分别为流动站和基准站天顶对流层湿延迟参数,估计策略采用随机游走过程,MF为对流层投影函数,本文采用NMF函数。
2 实验及结果分析 2.1 实验数据选取我国不同纬度范围内的天津、武汉和广东CORS站网多天BDS实测数据,组成不同长度的基线进行解算,具体信息见表 1。由于实际动态环境变化复杂,受影响因素多,数据连续性差,较难获取长时间的动态连续观测数据,所以本文选用静态模拟动态(采用动态解算策略处理静态数据)的处理分析方法,以期评估出目前区域导航星座下,在我国不同地域进行中长基线的动态定位时所能达到的性能。
|
|
表 1 基线的基本信息 Tab. 1 Baselines' information |
本文后续的数据处理基于作者所研制的高精度GNSS动态定位测速与定姿软件KinPOS V2.0完成,该软件采用上述的中长基线相对定位模型。具体解算策略见表 2。
|
|
表 2 估计参数及其处理策略 Tab. 2 Estimation parameters and strategy |
由于目前BDS系统还是局域星座,不同时段的卫星几何结构差异较大,为了分析不同观测时段北斗中长基线动态解算性能差异,并保证每个时段都有足够的收敛时间,本文按8 h的时长将每天的观测数据划分为3个时段:第1时段为LT(地方时)08:00~16:00,第2时段为LT 16:00~24:00,第3时段为LT 00:00~08:00。对各个时段的BDS观测数据按照上述策略分别进行处理,然后统计中长基线的模糊度首次固定时间和定位精度。
2.3 首次固定时间分析首次正确固定时间(TTFF)是指接收机从接收到有效的观测数据到解算得到第1个正确的模糊度固定解所需要的时间。为保证评估结果的可靠性,本文采用较为严格的评判标准,即如果解算结果同时满足以下3个条件,则认为当前历元正确固定,并以此作为确定TTFF的标准:1)模糊度解算的ratio检验值大于所设阈值2.5;2)固定后的基线分量在水平方向上偏差小于0.1 m,高程方向上偏差小于0.2 m;3)当前历元以及之后连续5 min(300个历元)之内都满足条件1)和2)。
对天津和武汉的3条基线多天的动态首次固定时间进行统计,得到各条基线不同时间段的首次固定时间,如图 1和图 2所示。可以看出,位于武汉CORS站网的3条基线在不同时段内TTFF大约在2~3 h,而天津CORS站网的3条基线在不同时段TTFF变化较大,从1 h到5 h不等,总体上要长于武汉CORS网的基线。
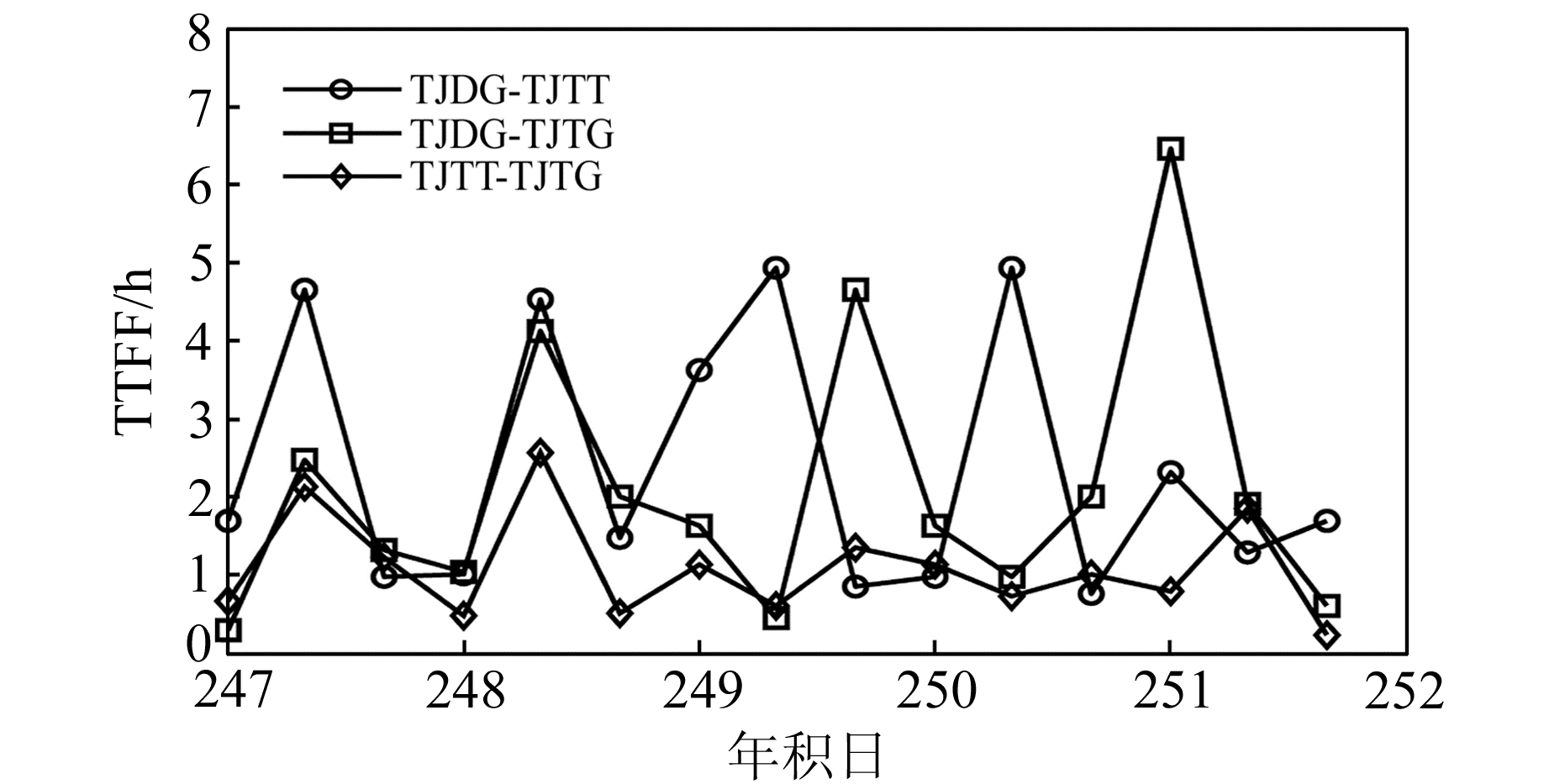
|
图 1 天津3条基线不同时段的首次固定时间 Fig. 1 TTFF in different periods of three baselines in Tianjin CORS |
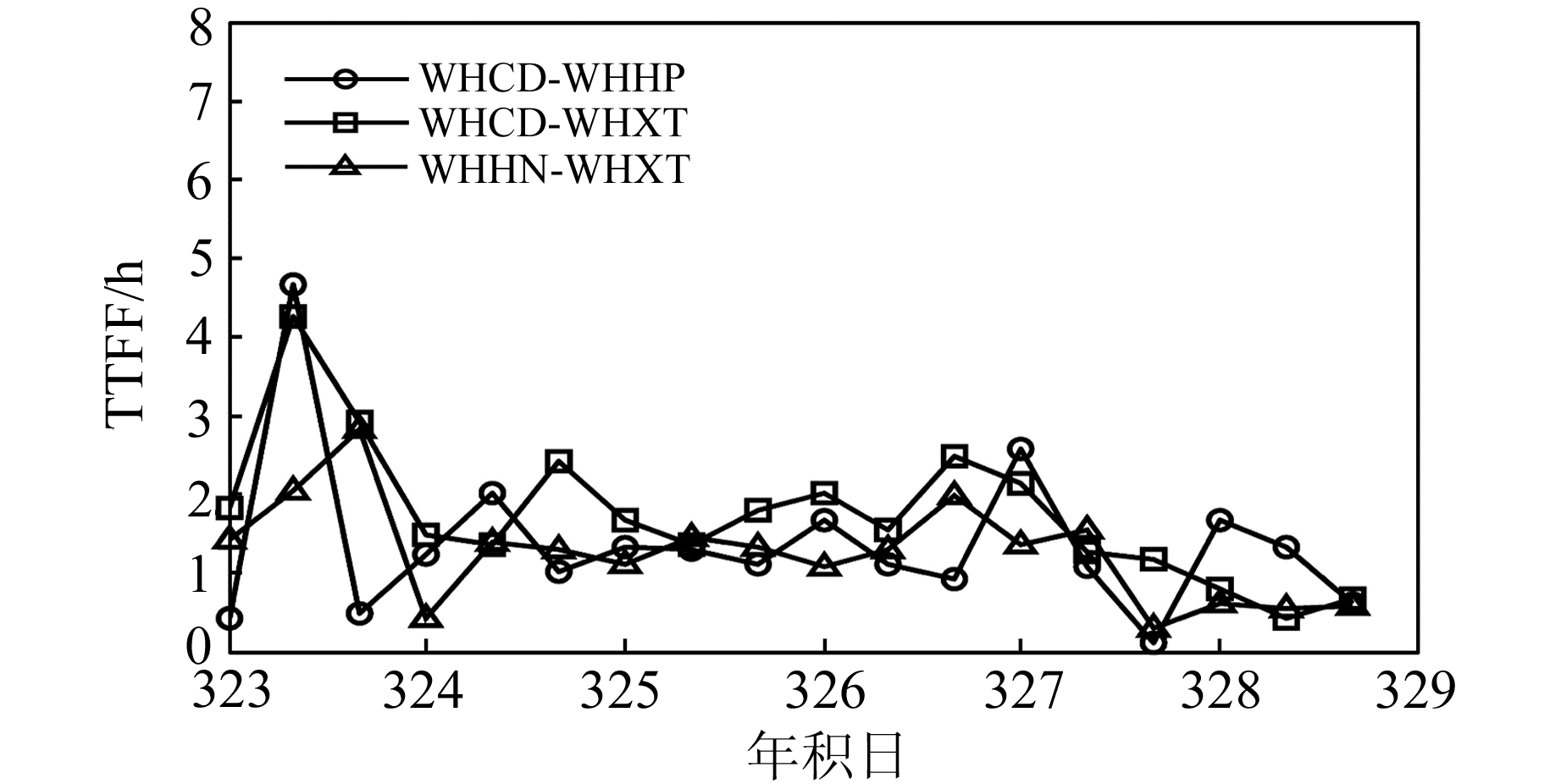
|
图 2 武汉3条基线不同时段的首次固定时间 Fig. 2 TTFF in different periods of three baselines in Wuhan CORS |
各基线不同时段的多天平均TTFF统计结果如图 3和图 4所示。可以看出,各基线的平均TTFF从1 h至4 h不等,大部分的平均固定时间在2.5 h以内,位于广东的CZGT-JSGT部分时段的平均TTFF甚至在20 min以内。整体上,不同区域的基线TTFF存在差异,天津最长,其次为武汉,广东最短。从图 4可知,TTFF主要分布在50 min以内、50~100 min和100~150 min 3个区间,各占25.9%、41.7%和19.4%,总体上TTFF在2.5 h以内的时段比例超过87.0%。
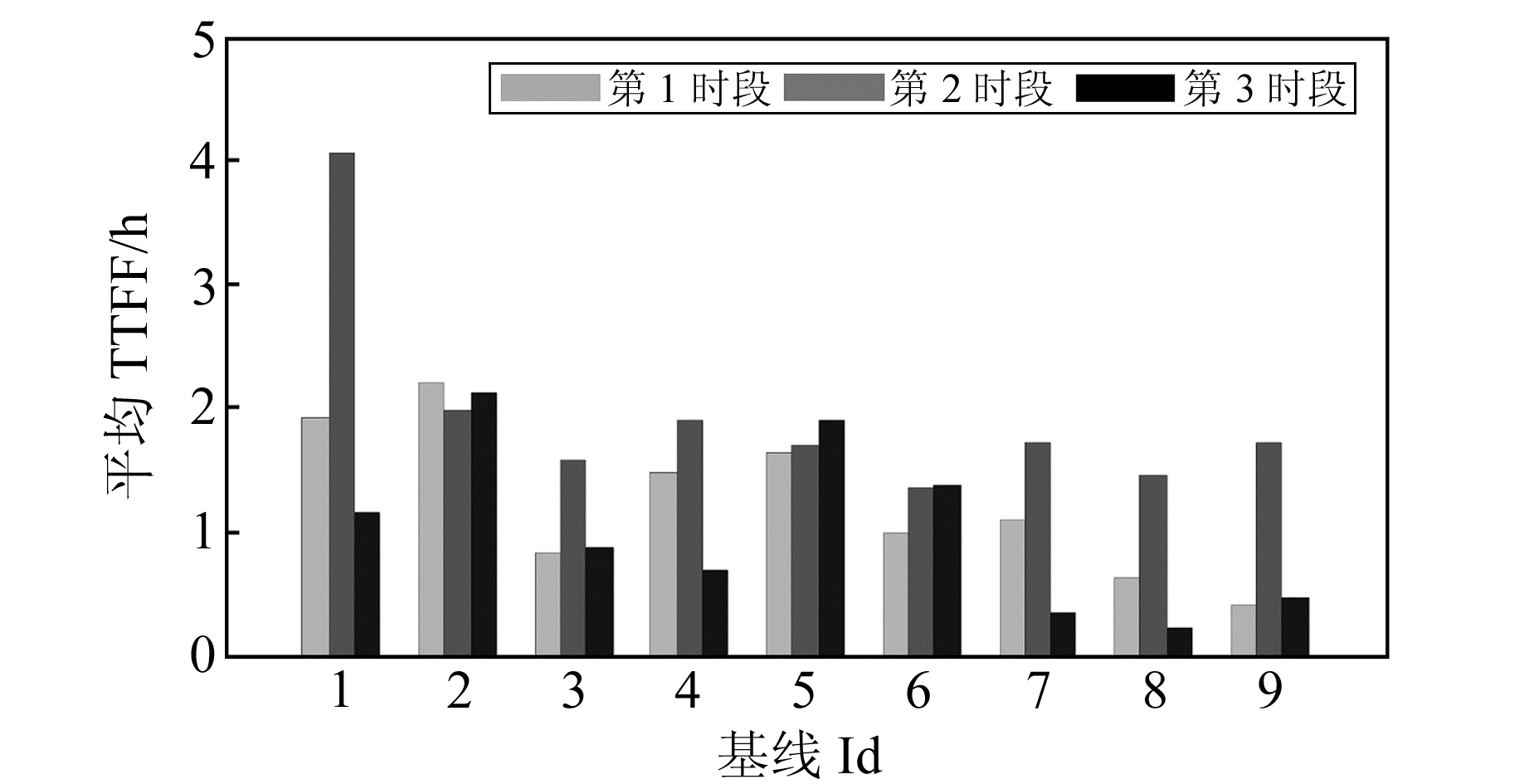
|
图 3 各基线不同时段的平均首次固定时间 Fig. 3 Average TTFF in different periods of each baseline |
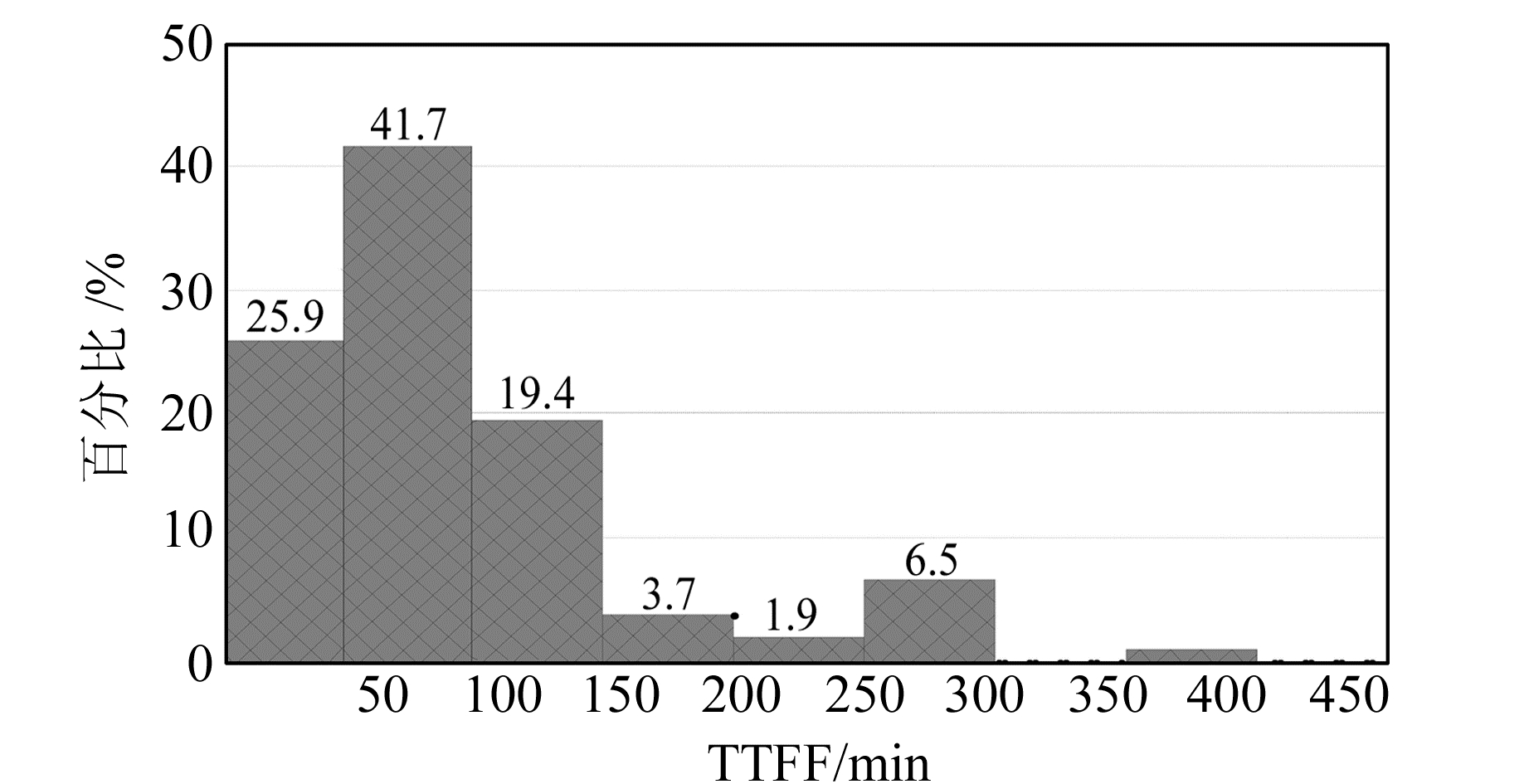
|
图 4 中长基线首次固定时间分布 Fig. 4 Distribution of TTFF of medium-long baseline |
表 3统计了各条基线不同天多个时段解算的平均TTFF。整体上来看,位于天津的基线TTFF最长,平均TTFF接近2 h;位于武汉的基线平均TTFF接近1.5 h;位于广东的基线TTFF最短,平均TTFF不到1 h,所有基线TTFF的平均值约为84 min。由此可见,目前BDS中长基线动态定位首次固定时间与测站的地理纬度存在明显的相关性,纬度越高,TTFF越长,反之则越短。在中国北方至少需要2 h才能得到稳定可靠的固定解,中部地区需要约1.5 h,在中国南方1 h就能获得固定解。
|
|
表 3 各基线解算的平均首次固定时间 Tab. 3 Average TTFF of each baseline |
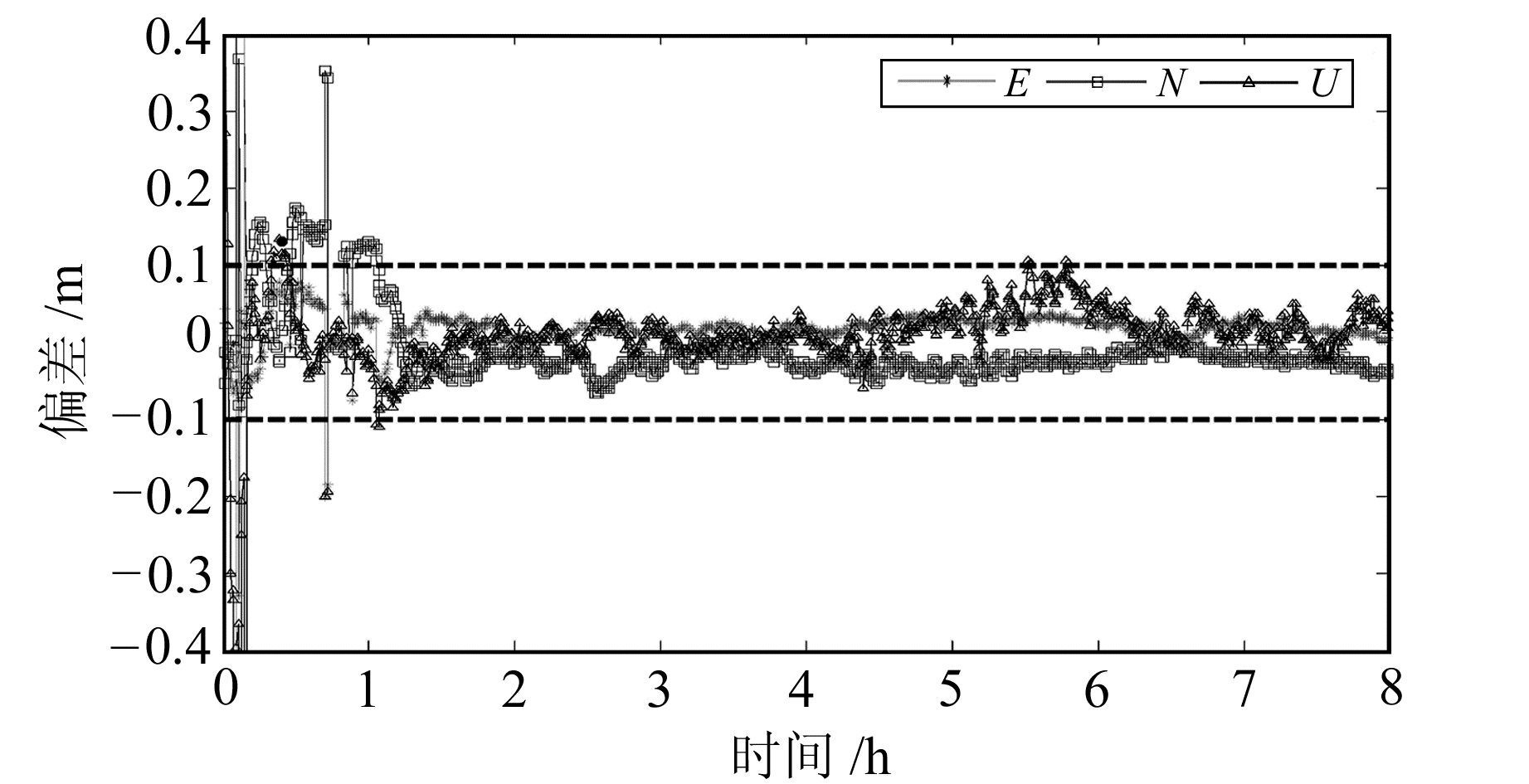
在评估基线解算精度时,以CORS站网提供的精确已知值作为参考真值。图 5~7给出了基线TJDG-TJTT第247天第1时段、WHCD-WHHP第324天第1时段和GDJL-XNGT第317天第1时段定位的偏差序列。可以看出,收敛之后,基线E、N和U3个方向上的定位偏差都在10 cm以内。TJDG-TJTT收敛后基线E、N和U分量的统计精度分别为4.08 cm、2.08 cm和5.80 cm;WHCD-WHHP的解算精度在E、U方向上优于TJDG-TJTT,N方向上则稍差一些,分别为2.15 cm、2.82 cm和3.18 cm;GDJL-XNGT的解算精度最优,其E、N和U方向上的统计精度为别为0.81 cm、1.06 cm、3.52 cm。需要注意的是,TJDG站在GPST 06:39:30出现了约1 min的数据中断,使得TJDG-TJTT在最后一段出现了重新收敛的现象。

|
图 5 TJDG-TJTT第247天第1时段定位偏差序列 Fig. 5 Position bias of TJDG-TJTT in the first periodof DOY 247 |
|
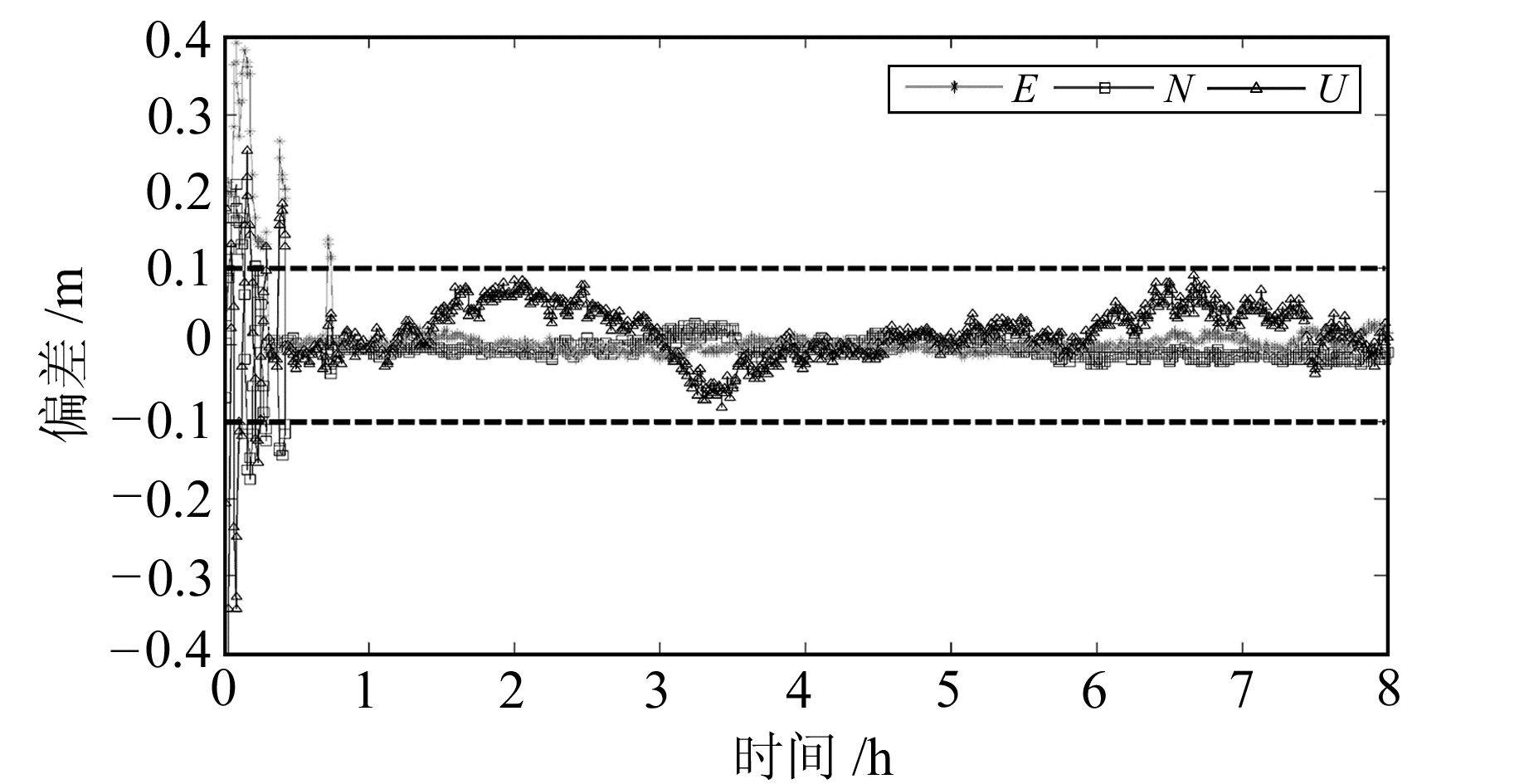
图 6 WHCD-WHHP第324天第1时段定位偏差序列 Fig. 6 Position bias of WHCD-WHHP in the first period of DOY 324 |
|
图 7 GDJL-XNGT第317天第1时段定位偏差序列 Fig. 7 Position bias of GDJL-XNGT in the first period of DOY 317 |
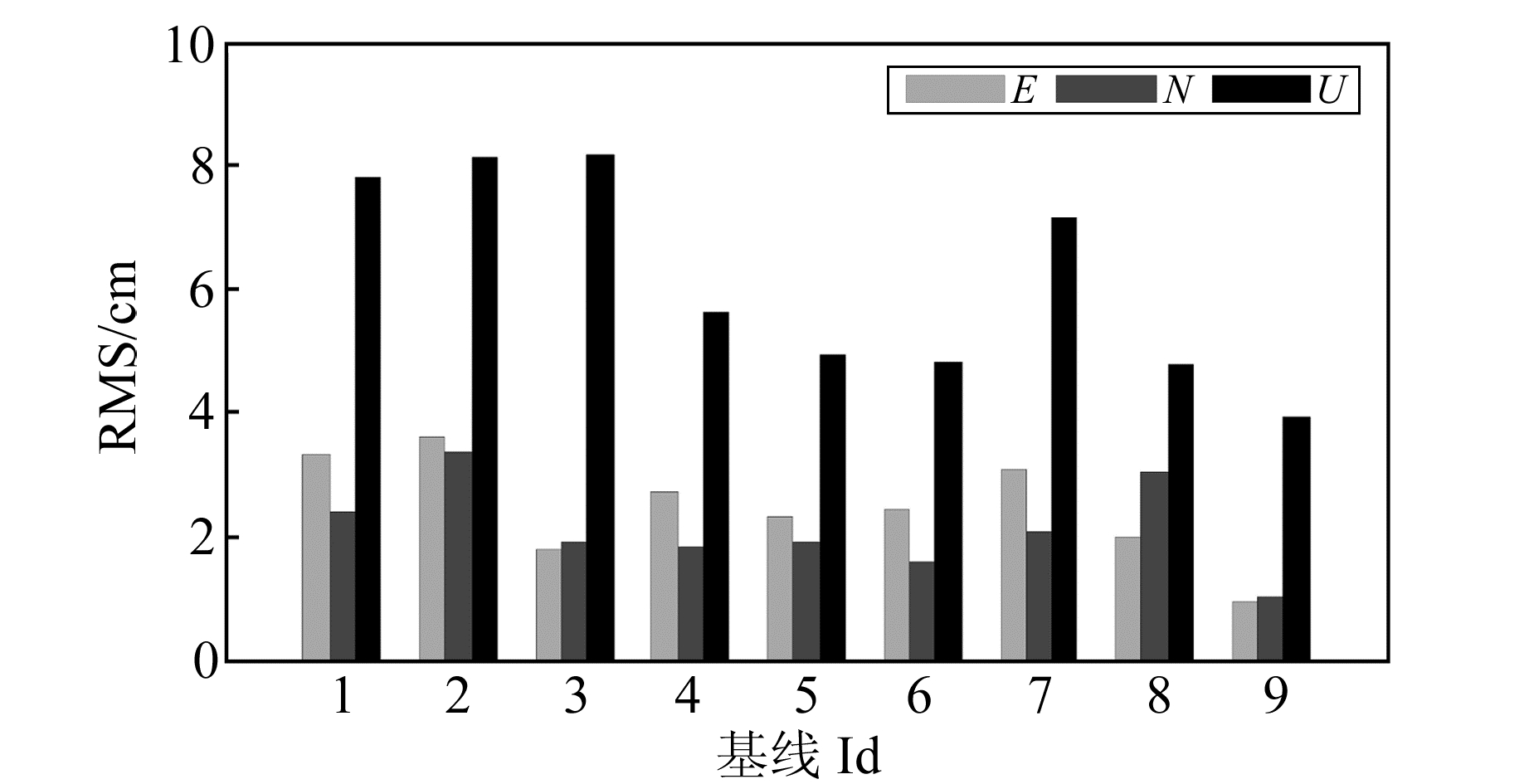
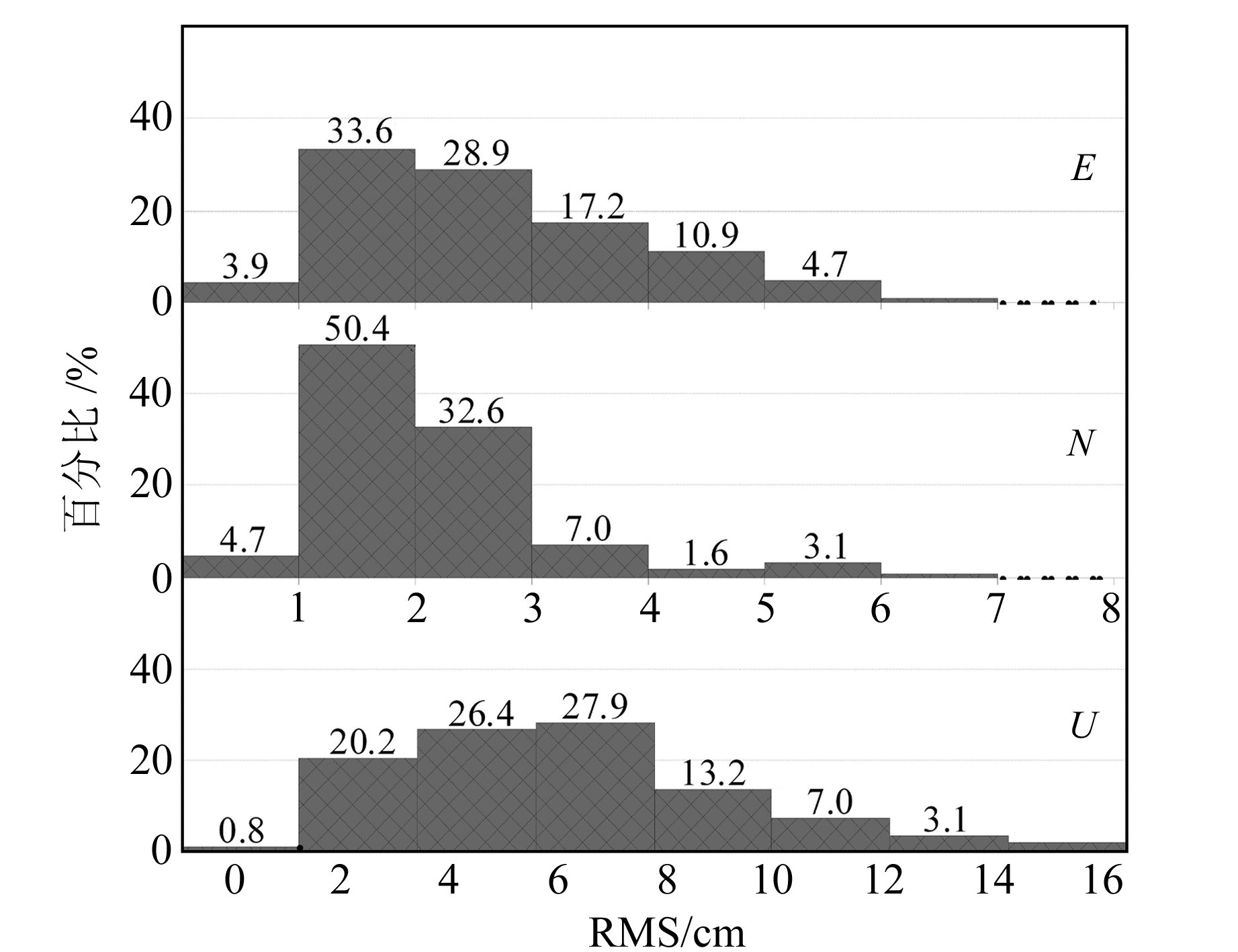
图 8和图 9给出了各基线的平均定位精度RMS和定位偏差分布。可以看出,各条基线不同时段的平均定位精度RMS在E、N方向优于4 cm,高程方向优于8 cm。由表 4可见,位于天津的3条基线的定位结果总体上稍差,特别是高程方向,位于武汉和广东的3条基线解算精度相当;不同区域不同基线的E、N和U方向的平均RMS分别为2.5 cm、2.1 cm和6.1 cm。上述结果表明,对于BDS中长基线动态定位来说,在模糊度正确固定后,基线水平精度能够达到2~4 cm,高程精度为4~7 cm,可以实现亚dm级动态定位。
|
图 8 各基线不同时段的平均定位精度RMS Fig. 8 Average RMS in different periods of each baseline |
|
图 9 中长基线定位偏差分布 Fig. 9 Distribution of position bias of medium-long baseline |
|
|
表 4 各基线解算的基线分量统计精度RMS Tab. 4 RMS of each baseline in east/north/up component |
本文首先给出了基于BDS三频观测值的中长基线动态相对定位的数学模型及误差处理措施,在此基础上分别利用天津、武汉和广东CORS站网内的实测数据,对BDS中长基线动态定位的TTFF和定位精度进行了评估分析。结果表明:1)对于目前的北斗区域系统而言,BDS中长基线动态定位的TTFF与测站纬度具有明显相关性,我国北方地区的平均TTFF约为2 h,中部地区约为1.5 h,南方地区不到1 h;2)TTFF与观测时段也具有较强的关系,且不同时段的TTFF差别较大,本文中时段1(当地时间08:00~16:00)和时段3(00:00~08:00)的固定时间较短,而时段2(16:00~24:00)的固定时间普遍较长;3)模糊度正确固定以后,不同区域不同时段的BDS中长基线动态定位精度相差不大,水平RMS为2~4 cm,高程RMS为4~7 cm。
随着我国北斗系统全球星座的建设,BDS卫星的分布将更加均匀,站星之间的几何图形结构将得到极大的改善,BDS中长基线的定位性能自然也会得到进一步的提升。
| [1] |
何俊, 刘万科, 张小红. 北斗短基线三频实测数据单历元模糊度固定[J]. 武汉大学学报:信息科学版, 2015, 40(3): 361-365 (He Jun, Liu Wanke, Zhang Xiaohong. Single Epoch Ambiguity Resolution of BDS Triple Frequency Measured Data Under Short Baseline[J]. Geomatics and Information Science of Wuhan University, 2015, 40(3): 361-365)
(  0) 0) |
| [2] |
Zhao S H, Cui X W, Feng G, et al. A Kalman Filter-Based Short Baseline RTK Algorithm for Single-Frequency Combination of GPS and BDS[J]. Sensors, 2014, 14(8): 15415-15433 DOI:10.3390/s140815415
(  0) 0) |
| [3] |
赵祥伟. 中长基线下GNSS动态相对定位算法与实现[D]. 北京: 中国矿业大学, 2015 (Zhao Xiangwei. Algorithms and It's Realization of GNSS Medium-Long-Baseline Dynamic Relative Positioning[D]. Beijing: China University of Mining and Technology, 2015) http://cdmd.cnki.com.cn/Article/CDMD-10290-1015972030.htm
(  0) 0) |
| [4] |
李博峰, 沈云中, 周泽波. 中长基线三频GNSS模糊度的快速算法[J]. 测绘学报, 2009, 38(4): 18-23 (Li Bofeng, Shen Yunzhong, Zhou Zebo. A New Method for Medium and Long Range Three Frequency GNSS Rapid Ambiguity Resolution[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 18-23)
(  0) 0) |
| [5] |
祝会忠, 徐爱功, 高猛, 等. BDS网络RTK中距离参考站整周模糊度单历元解算方法[J]. 测绘学报, 2016, 45(1): 50-57 (Zhu Huizhong, Xu Aigong, Gao Meng, et al. The Algorithm of Single-Epoch Integer Ambiguity Resolution between Middle-Range BDS Network RTK Reference Stations[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 50-57)
(  0) 0) |
| [6] |
刘鸣, 柴洪洲, 董冰全. 北斗网络RTK基准站间整周模糊度快速确定方法[J]. 信息工程大学学报, 2016, 17(6): 760-763 (Liu Ming, Chai Hongzhou, Dong Bingquan. Algorithm of Instantaneous Integer Ambiguity Resolution for Reference Stations of BDS Network RTK[J]. Journal of Information Engineering University, 2016, 17(6): 760-763)
(  0) 0) |
| [7] |
李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2016 (Li Zhenghang, Huang Jinsong. GPS Surveying and Data Processing[M]. Wuhan: Wuhan University Press, 2016)
(  0) 0) |
| [8] |
刘万科, 任杰, 曾琪, 等. 2013~2015年BDS空间信号测距误差的精度评估[J]. 国防科技大学学报, 2016, 38(3): 1-6 (Liu Wanke, Ren Jie, Zeng Qi, et al. Accuracy Assessment of BDS Signal-in-Space Range Errors in 2013-2015[J]. Journal of National University of Defense Technology, 2016, 38(3): 1-6 DOI:10.11887/j.cn.201603001)
(  0) 0) |
| [9] |
Teunissen P J G. The Least-Squares Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy, 1995, 70(1): 65-82
(  0) 0) |
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, 129 Luoyu Road, Wuhan 430079, China;
3. Airborne Remote Sensing and Mapping Institute of Inner Mongolia, 42 South-Xing'an Road, Hohhot 010051, China
 2018, Vol. 38
2018, Vol. 38


