2. 中国科学院大学,北京市玉泉路19号甲,100049;
3. 中国地震局地球物理勘探中心,郑州市文化路75号,450002;
4. 中国科学技术大学地球和空间科学学院,合肥市金寨路96号,230026
地震噪声是影响地震数据可用性的重要因素,按频率可分为低频噪声(< 1 Hz)和高频噪声(>1 Hz),其中高频噪声可通过安装井下地震计进行压制[1-2]。鉴于井下地震计对于高频噪声压制的有效性,其记录数据在地震学研究中发挥了重要的作用,并应用于越来越多的地区[3-4]。井下地震计噪声强度通常随安装深度增加而降低[1, 5],但安装费用会随安装深度增加而大幅增加,所以安装深度的确定需要综合考虑埋深及安装费用。为确定合适的井下地震计安装深度,需要对噪声波场以及井下地震计噪声强度随安装深度的变化规律有充分的认识。Carter等[1]分析纽约Adirondack lowlands硬质岩石地表台站以及埋深945 m的深井台站记录数据发现,频率范围15~40 Hz时,深井台记录噪声强度相较地表台低10 dB;而40~100 Hz时深井台噪声强度较地表台低20 dB以上。Boese等[2]在分析新西兰Auckland城区井下地震计噪声信号时发现,在2~8 Hz频段,26 m深度井下台较地表台噪声强度降低3 dB,383 m深度井下台噪声强度较地表台下降10 dB;而在8~35 Hz频段,26 m井下台较地面台有更高的噪声强度。井下地震计高频噪声强度随深度减小,但可能在某一深度突变,这可能是由于特定的速度结构导致的,然而尚缺乏相应的数值模拟研究[2]。
除了数值模拟,观测实验也是研究空气中声波在井下地震计记录强度特征的有效方法。本文选择2015-08-12天津爆炸作为观测实验的事件,该事件能量较大[6],可被天津及周边台网的井下地震计记录,且该区域有较好的速度结构研究基础[4, 7]。首先基于射线理论给出井下地震计噪声强度随安装深度变化的直观结果;然后根据理论地震图测量的声波转换波/P波振幅比,分析井下地震计安装深度、速度以及衰减结构等对井下地震计噪声强度的影响,最后结合天津爆炸事件数据,分析实际观测中井下地震计噪声强度的特征。本文综合上述研究成果,给出了井下地震计的推荐安装深度。
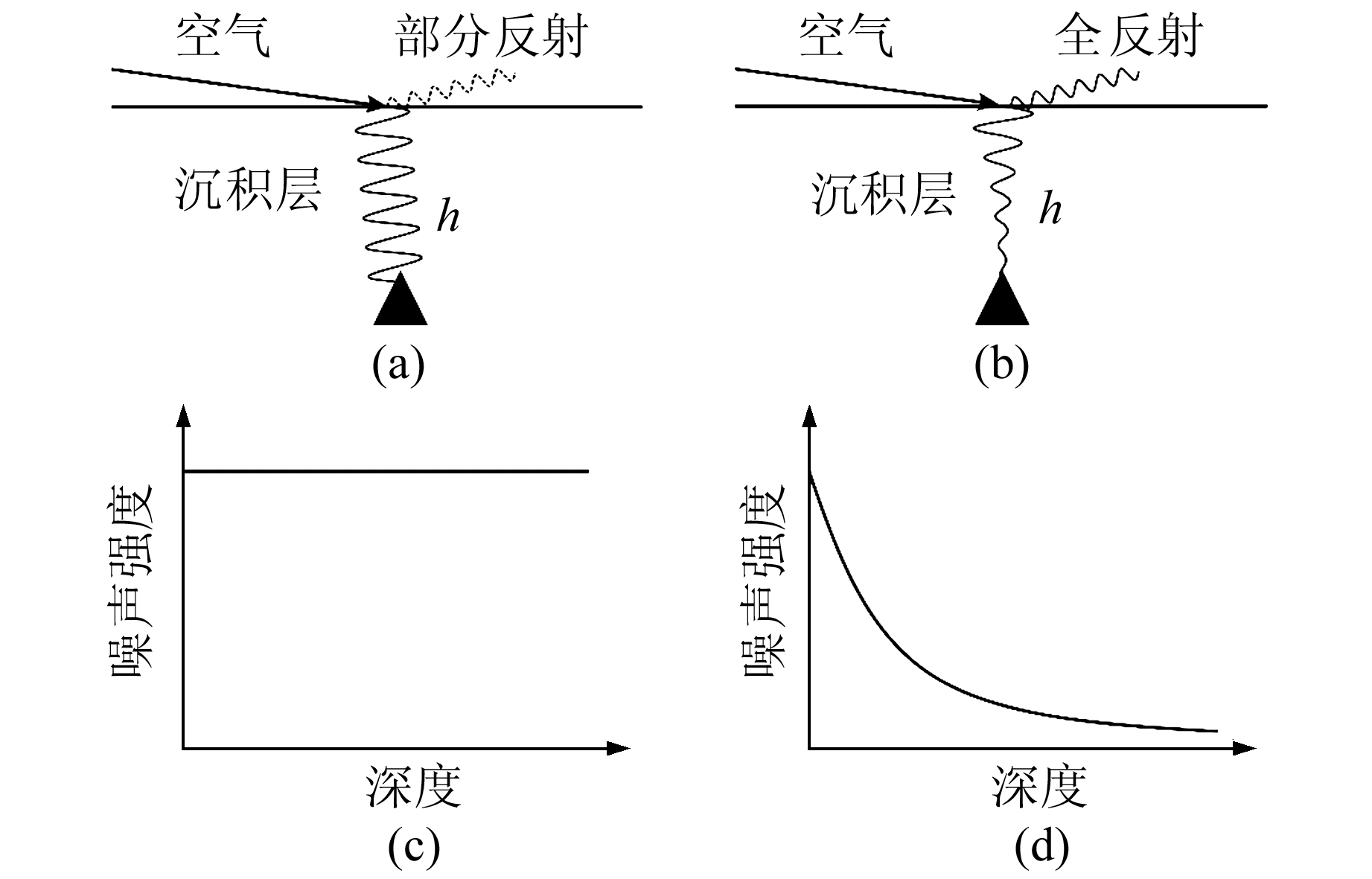
1 基于模拟波形的井下地震计噪声强度特征对于空气中声波直接与固体地球耦合的情况,首先给出基于射线理论的直观认识。如图 1所示,假定空气中声波沿水平方向传播(源与台站的水平距离远大于垂向距离)。由于近地表P波波速显著大于声波速度,沉积层覆盖等区域S波速度与声波速度可比,本文仅讨论S波速度与声波速度不同情况下的结果。当近地表S波速度小于声波速度时,空气中声波主要能量透射进入沉积层,少量能量反射回空气层,此时近地表声波转换波振幅随深度不变;当近地表S波速度大于声波速度时,空气中声波全反射回空气层,少量能量进入沉积层,此时近地表声波转换波振幅随深度迅速衰减。
|
图 1 井下地震计记录空气转换波特征 Fig. 1 Characteristics of converted acoustic waves recorded by borehole seismometers (a)、(c)分别为固体介质S波速度小于声速时, 声波转换波在界面传播示意图、噪声强度随台站埋深的变化特征; (b)、(d)为S波速度大于声速的情况 |
利用合成理论地震图可有效研究复杂结构下的空气中声波转换波特征。本文选择FK方法合成理论地震图,该方法对频率和波数进行积分,采用传播矩阵计算台站的位移,可合成准确的地震波形[8]。
利用FK方法模拟地震波形分为格林函数计算和地震图合成两个部分,其中计算格林函数需要设置合适的源参数、台站位置、速度结构以及时间参数。本文震源使用中心频率为5 Hz的爆炸源,震源函数取高斯函数,源距地面高取1 m;台站设置方面,震中距取10 km,台站均匀分布在1~500 m埋深范围内;设置2层模型,包括半无限空气层和半无限固体层。空气层P波速度取340 m/s,密度取1.29 kg/m3。FK中不能直接处理流体情况,空气层S波速度取1×10-5 km/s。固体层P波速度取1.8 km/s,密度取2 000 kg/m3[4]。为研究不同S波速度对井下地震计记录空气中声波强度的影响,S波速度分别取0.2 km/s、0.3 km/s、0.4 km/s、0.5 km/s。在考虑衰减结构的影响时,QS分别选取500、80,QP取QS的2倍[4]。由于源主频为5 Hz,对应周期为0.2 s,为刻画该周期特征,选择时间间隔约为0.05 s,计算点数取2 048,对应计算时长为100 s。地震图合成需要输入震源参数。对于本文爆炸源情况,仅需指定M0值,使用1014 Nm(对应震级ML2.9)。为验证本文中地震波模拟的正确性,对比高精度数值模拟方法SEM和FK合成的理论地震图,发现两者模拟波形近乎一致。
本文使用声波转换波/P波振幅比(简称振幅比)刻画声波转换波在井下地震计记录的振幅特征。振幅比测量中选择P波振幅作为参考是由于P波是初次波,不易受其他震相干扰且容易辨认。振幅比测量流程为:对波形进行2~5 Hz滤波,取绝对值,根据P波、声波转换波理论到时截取波形,读取振幅,计算振幅比。选择2~5 Hz是由于该频段是声波转换波的优势频段[9]。需要注意的是,截取波形的时间窗长通过波形分析来确定,一般情况下P波和声波时间窗长均选择2 s,但VS=0.4 km/s时,为减小Rayleigh面波对声波转换波的干扰,时间窗长选为0.2 s。
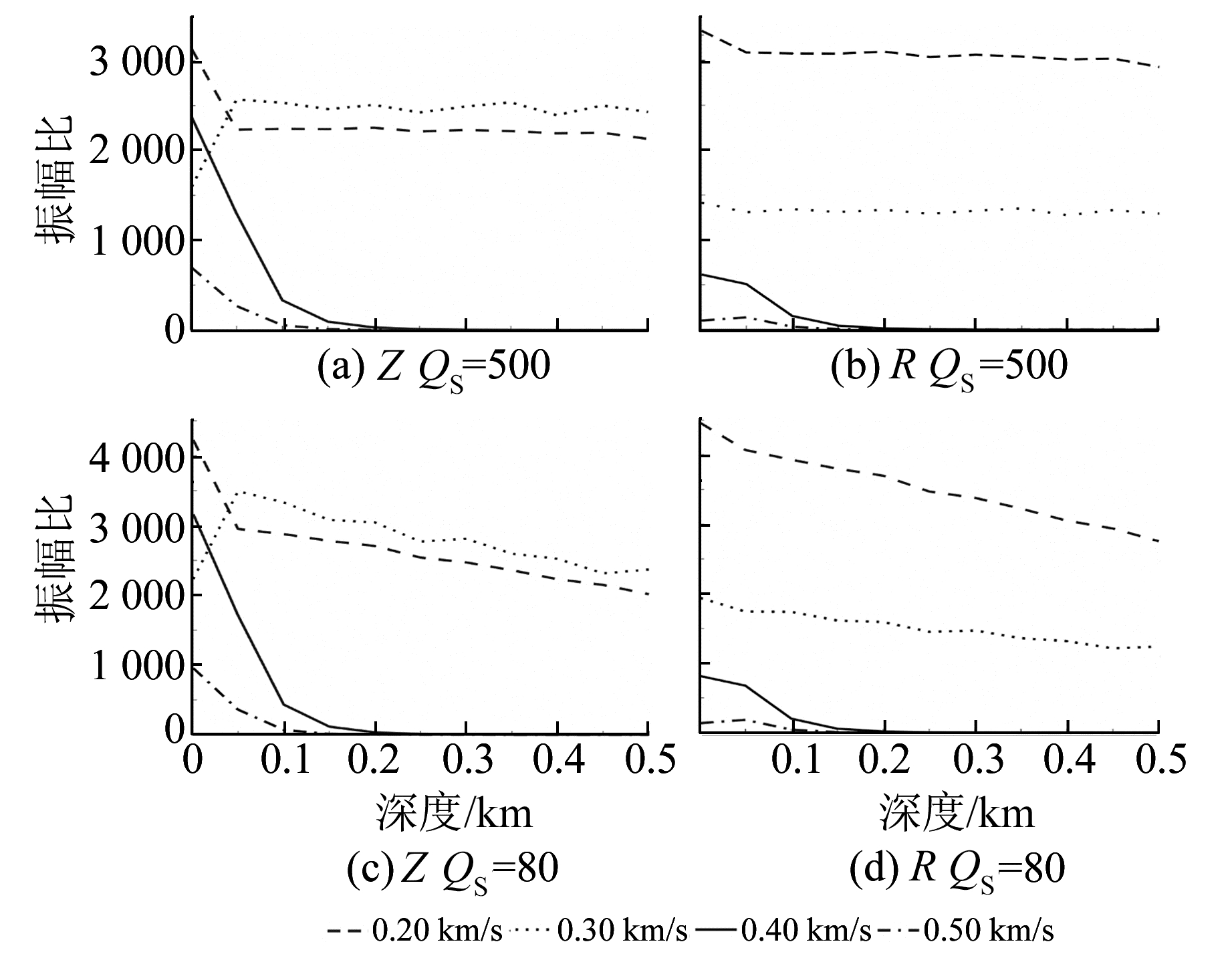
图 2为测量得到的振幅比。从图中可见,弱衰减情况下(QS=500、QP=1 000),固体介质S波速度与声波速度的关系影响振幅比随深度的特征。固体介质S波速度小于声波速度时,振幅比随台站深度几乎不变,而固体介质S波速度大于声波速度时,振幅比随台站埋深指数减小,且固体介质S波波速越大,振幅比值越小,这与基于射线理论的结果一致。Z分量、R分量在S波速度不同时有不同的振幅比,这主要是空气中声波转换为S波的出射角不同及S波的偏振特性所致。该Z、R比与射线理论的预测结果一致,表明振幅比测量的准确性。固体介质S波速度小于声波速度时,埋深小于50 m出现的振幅比与其他深度下值相差较大可能是声波转换为P波的影响。强衰减的情况下(QS=80、Qp=160),固体介质S波速度小于声波速度的振幅比随台站深度呈线性减小趋势,这是由于声波转换波、P波受衰减结构影响振幅减小,而声波转换波主要为S波,当台站埋深越深时,声波转换波在固体介质传播的路程越远,因此受Q值影响更大。由于近地表台站波形几乎不受Q值影响,因此强衰减情况与弱衰减情况Z、R各分量在近地表有相近的振幅比。
|
图 2 固气半空间模型声波转换波/P波振幅比随台站埋深的变化 Fig. 2 C/P (converted acoustic wave/P wave) ratio versus depth for solid-air half space models 图例表示固体介质S波速度; (a)、(b)分别为强衰减情况下的垂向、径向分量振幅比; (c)、(d)为弱衰减情况下对应的振幅比 |
上述基于两层半无限空间模型得到的振幅比结果为理解复杂情况下振幅比奠定基础。然而实际情况下,S波、P波速度一般随深度逐渐增加,因此本文分别考虑S波速度随深度线性、幂指数增加的情况。根据前人的研究成果[4, 7],P波速度在近地表取1.8 km/s,在1 km深度处取4.0 km/s,S波速度在近地表取0.2 km/s,在1 km深度处取1.0 km/s,建立速度随深度线性增加模型。对于速度随深度幂指数增加的情况,由于P波速度对井下地震计噪声强度的影响较小,因此P波速度仍设为线性增加,而S波速度使用式(1)进行计算:
| $ {V_{\rm{S}}} = a + b{h^c} $ | (1) |
式中,a取200,b取94,c取0.31,h单位为m,VS单位为m/s。密度根据如下经验公式[10]求得:
| $ \rho = dV_{\rm{P}}^e $ | (2) |
式中,d取1.74,e取0.25,VP单位为m/s,ρ单位为g/cm3,模型中QS取80,QP取QS的2倍。
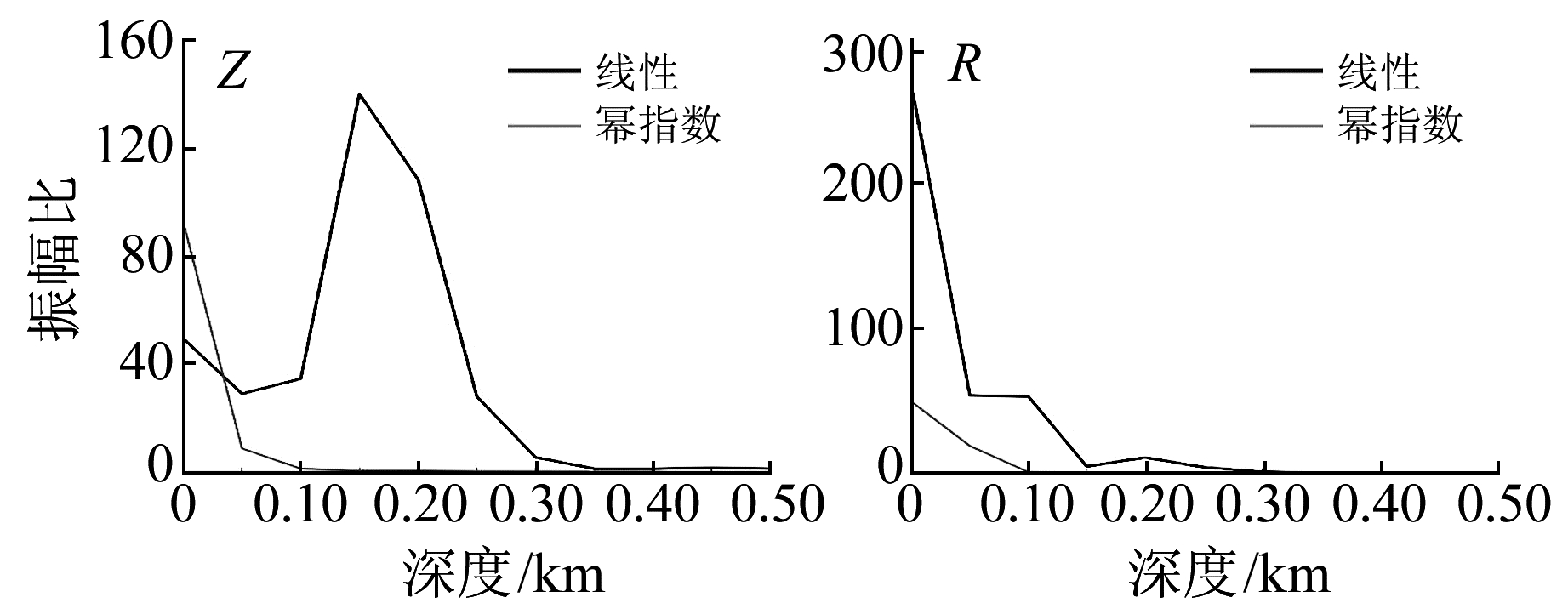
图 3为S波速度随深度线性及幂指数增加情况下的振幅比。从图中可见,S波波速随深度线性增加情况下,Z分量振幅比在0~0.10 km深度范围变化较小,在0.10~0.15 km振幅比增加,在0.15~0.50 km振幅比迅速降低,且低于0~0.10 km对应值;R分量声波转换波/P波随深度大致呈减小趋势,且振幅比在0~0.05 km深度范围下降剧烈。S波速度随深度线性减小情况下的振幅比变化特征与S波速度与声波速度相近的深度相关。当S波速度与声波速度相等时,声波转换波近乎水平方向传播,考虑S波的偏振特征,此时Z分量振幅最大,相应R分量振幅最小,这与基于模拟波形测量得到的振幅比一致。S波波速随深度幂指数增加情况下,无论是Z分量还是R分量振幅比均随深度增加迅速衰减,这是由于该速度模型下,S波速度与声波速度相等的深度接近于地表,使得浅地表以下S波速度大于声波速度。
|
图 3 S波随深度线性及幂指数增加模型下的Z分量、R分量声波转换波/P波振幅比随深度的变化 Fig. 3 C/P ratio versus depth of Z and R components for models with VS increasing linearly and power-exponentially S波随深度线性及幂指数增加模型下的Z分量、R分量声波转换波/P波振幅比随深度的变化 |
2015-08-12 15:30(UTC)天津某处(39.04°N,117.74°E)发生强烈爆炸,天津及周边地震台网记录到该次事件,事件及50 km范围内台站位置如图 4(a)所示,这些台站均安装井下地震计,埋深为270 m。

|
图 4 天津事件台站分布及波形 Fig. 4 Stations distribution of Tianjin explosions and seismograms (a)2015-08-12天津事件(五角星)、台站(三角形)分布图; (b)、(c)最近DAG台站记录波形宽频带及2~5Hz滤波波形对比图, P1、Sf1、A1分别表示第1次事件P波、面波、声波转换波, P2、Sf2、A2分别表示第2次事件; (d)震中距50km范围内台站三分量归一化振幅记录剖面图。波形左侧分别为台站名、距离、方位角(°), 其中灰色虚线、实线分别表示P波、声波转换波理论到时 |
图 4(b)、4(c)为离爆炸源最近的DAG台站(距离8.35 km,方位角208°)记录的宽频带三分量波形及其2~5 Hz滤波波形,其中水平分量旋转至R、T分量时,以1°为间隔搜索0°~179°P波R/T振幅极大值确定旋转方向。由图 4可发现,R分量P波震相清晰,而T分量P波难以观测,说明水平分量旋转的正确性。通过波形可知,该次爆炸包含2次事件,2次事件P波与面波的到时差一致。对比宽频带波形及2~5 Hz滤波波形发现,2~5 Hz滤波可减弱Rayleigh面波的影响,凸显声波转换波,该频率与前人选择的声波转换波优势频段一致[9]。此处选择能量更大的第二次事件波形进行分析。2~5 Hz滤波后,绘制记录剖面,以分析天津爆炸事件波形随震中距的特征。Z分量除BET台站声波转换波振幅大于P波振幅外,其余台站声波转换波振幅均小于P波振幅。根据声波转换波理论到时,发现Z分量部分台站声波信号明显,而其他台站声波信号不明显;R分量声波信号几乎所有台站均不明显;T分量理论上观测不到P波及声波转换波,此处可能是由于散射或起伏界面造成的。
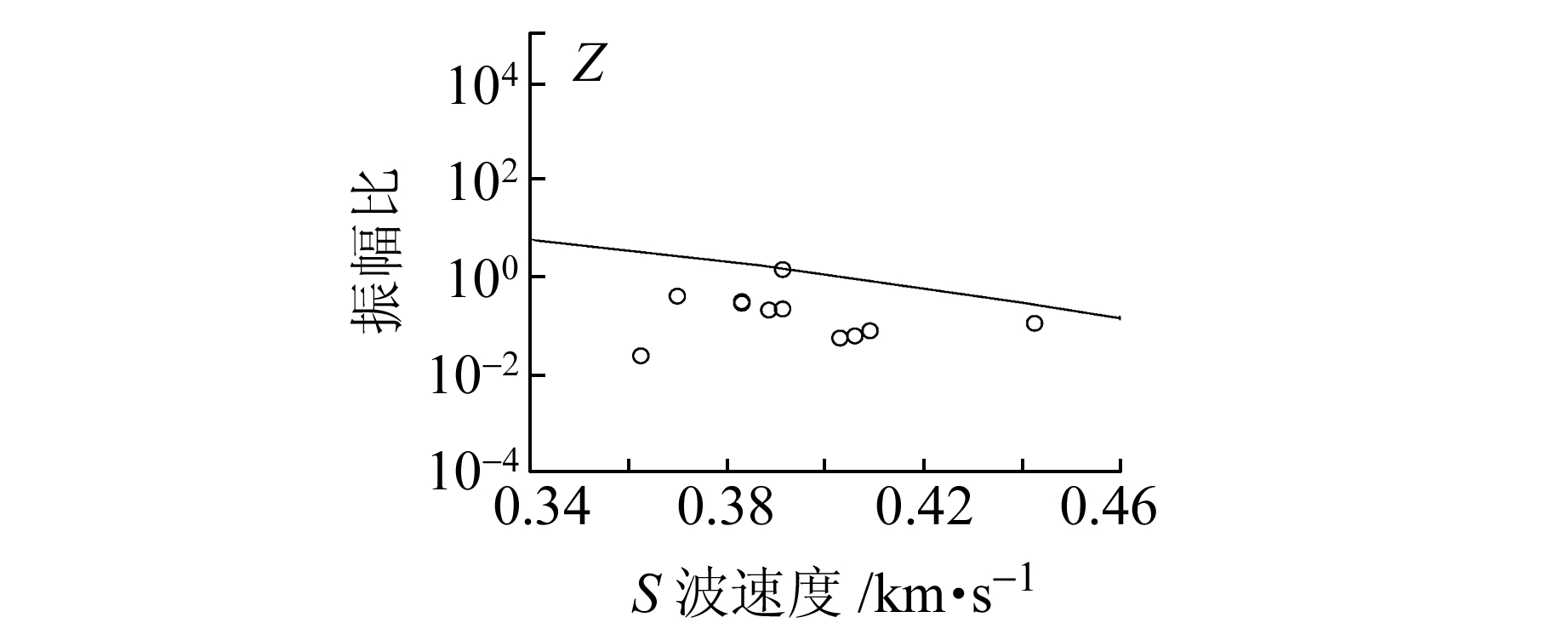
为分析基于实际数据的井下地震计噪声强度随S波速度的特征,采用与模拟数据相同的数据处理流程测量振幅比(图 5),其中测量振幅选取的窗长取2 s。为减少波形干扰对振幅比测量的影响,此处选择振幅更大的第二次事件波形测量振幅比。Z分量上振幅比大致随S波速度增加减小,R分量也观测到相似的特征。基于观测数据得到的振幅比与S波速度随深度指数增加模型模拟得到的振幅比接近,表明该区域S波速度随深度幂指数增加。通过天津爆炸事件观测数据,本文得到空气中声波在井下地震计记录强度的特征,虽然观测台站数目有限,但仍反映出其随S波速度的变化规律。
|
图 5 观测数据(点)及模拟数据(线)提取的声波转换波/P波振幅比随S波速度变化对比图 Fig. 5 C/P ratio versus VS from seismograms of Tianjin explosion (circles) and synthetic seismograms (line) for model with VS increasing power-exponentially 模拟波形使用VS深度幂指数变化的速度模型 |
为减弱空气中声波对台站的影响,井下地震计安装深度应大于参考深度即S波速度等于声波速度所对应的深度(图 6)。这是因为对于浅层S波速度小于声波速度的情况,空气中声波在地表转换为透射S波向固体浅层传播,该深度范围内声波转换波振幅大;而在VS大于声波速度的深度,透射S波不能向下传播,该深度范围内声波转换波振幅随深度增加指数衰减。相应地,由于固体介质P波速度相较声波速度大,因此空气中声波转换的P波在近地表即随深度指数衰减。以面波形式传播的噪声也随着深度的增加指数衰减。考虑声波转换波及以面波形式传播的噪声,井下地震计记录的噪声强度随深度变化的特征大致为在近地表指数衰减;在S波速度小于声波速度的深度范围内,噪声强度大致不变;在S波速度大于声波速度的深度范围,噪声水平指数下降,且整体噪声水平较低。

|
图 6 建议台站埋深及声波转换波路径示意图、噪声成分示意图及井下地震计记录噪声水平及井下地震计安装成本随台站埋深变化示意图 Fig. 6 Schematic diagram of suggested installation depth of borehole seismometers, and seismic noise of each component, and noise level of borehole seismometers and installation cost versus depth (a)建议台站埋深及声波转换波路径示意图; (b)噪声成分示意图, 点线、实线、点划线分别表示P波、S波、面波; (c)井下地震计记录噪声水平及井下地震计安装成本随台站埋深变化示意图图 6建议台站埋深及声波转换波路径示意图、噪声成分示意图及井下地震计记录噪声水平及井下地震计安装成本随台站埋深变化示意图 |
Boese等[2]通过不同埋深的井下地震计,分析了S波速度结构与噪声水平的关系,发现在2~5 Hz频率范围内,26 m埋深的井下地震计噪声水平相较地表台仅有很小的降幅,而383 m埋深的井下地震计噪声强度相较地表台减少多达10 dB。该现象可使用本文的结果解释,这是由于浅层S波速度约为300 m/s的沉积层,且S波速度随着深度增加迅速超过声波速度造成的。Prevedel等[11]给出的高频噪声水平随埋深指数衰减的特征与本文S波速度大于声波速度模型的预测结果一致。
然而,本文理论波形模拟时仅考虑了简单情况下的水平层状速度模型,实际情况中分界面可能不是水平的,例如起伏地形;弹性参数也不是随深度仅增加,例如Brocher对S波速度的测量中MCGY台站在埋深150 m以下有明显的速度值降低[10]。模拟中使用单个爆炸源,对于天津爆炸事件是合适的,但对于分析实际中更多类型的源,例如风、大气扰动、湍流等,单爆炸源不再合适。对于多源的情况可以理解为单源的叠加。另外,植被、建筑等对空气中声波在地面耦合有较大的影响,本文也未考虑此类影响。对于上述复杂模型,可通过SEM等数值方法模拟相应波形,并分析空气中声波在井下地震计记录强度的特征,这部分工作将在下一步研究中开展。
本文主要讨论远场声波转换波,即空气中声波在远场转换为地震波的情况,此时声波近水平方向传播,而空气中声波在近场也可以转换为P波、S波在固体介质中传播。由于空气层声波速度小于固体介质的P波速度(大约为固体介质P波速度的1/6),根据射线理论,其近场转换波的临界角较小,也就是说,近场的声波转换波仅在源附近的小块区域内转换,因此近场声波转换地震波仅影响源附近较小范围的台站。而本文讨论的远场声波转换波在近场、远场均可转换,对井下地震计噪声强度的影响更大。
4 结语本文模拟层状速度模型的理论地震图,测量其振幅比,得到台站埋深、S波速度以及衰减结构对井下地震计噪声强度的影响。结果表明,S波速度结构是影响井下地震计记录噪声强度的重要参数。分别得到2层半无限固气模型、S波速度随深度线性、幂指数增加模型的振幅比随深度的变化特征,发现深度浅于S波速度与声波速度相等深度时,振幅比随深度变化较小,但更深时,振幅比随深度指数下降。利用2015年天津爆炸事件在井下地震计台网的观测波形,分析井下地震计噪声强度随深度的变化特征,发现与S波速度随深度指数增加对应的振幅比有一致的结果,随着台站埋深增加振幅比减小。
S波速度与声波速度的相互关系是影响井下地震计噪声强度的重要指标,当埋深大于S波速度与声波速度相等的深度时,井下地震计记录受空气中声波的影响较小。为减弱空气中声波对井下地震计记录的影响,建议井下地震计安装深度应大于S波速度与声波速度相等的深度。
致谢 中国地震台网中心提供了波形数据,在此表示感谢。
| [1] |
Carter J A, Barstow N, Pomeroy P W, et al. High-Frequency Seismic Noise as a Function of Depth[J]. Bulletin of the Seismological Society of America, 1991, 81(4): 1 101-1 114
(  0) 0) |
| [2] |
Boese C, Wotherspoon L, Alvarez M, et al. Analysis of Anthropogenic and Natural Noise from Multilevel Borehole Seismometers in an Urban Environment, Auckland, New Zealand[J]. Bulletin of the Seismological Society of America, 2015, 105(1): 285-299 DOI:10.1785/0120130288
(  0) 0) |
| [3] |
Abercrombie R E. Earthquake Source Scaling Relationships from -1 to 5 ML Using Seismograms Recorded at 2.5-km Depth[J]. Journal of Geophysical Research: Solid Earth, 1995, 100(B12): 24015-24036 DOI:10.1029/95JB02397
(  0) 0) |
| [4] |
Chong J J, Ni S D. Near Surface Velocity and QS Structure of the Quaternary Sediment in Bohai Basin, China[J]. Earthquake Science, 2009, 22(5): 451-458 DOI:10.1007/s11589-009-0451-1
(  0) 0) |
| [5] |
Barstow N, Carter J A, Pomeroy P W, et al. High Frequency (1~100 HZ) Noise and Signal Recorded at Different Depths in a Mine, Northwest Adirondacks, NY[J]. Geophysical Research Letters, 1990, 17(6): 681-684 DOI:10.1029/GL017i006p00681
(  0) 0) |
| [6] |
Li J, Tian B F. Refined Locations of Major Explosions in Tianjin Harbor[J]. Sci Bull, 2015, 60(21): 1 868-1 870 DOI:10.1007/s11434-015-0913-x
(  0) 0) |
| [7] |
Xie J J, Zimmaro P, Li X J, et al. VS30 Empirical Prediction Relationships Based on a New Soil-Profile Database for the Beijing Plain Area, China[J]. Bulletin of the Seismological Society of America, 2016, 106(6): 2 843-2 854 DOI:10.1785/0120160053
(  0) 0) |
| [8] |
Zhu L P, Rivera L A. A Note on the Dynamic and Static Displacements from a Point Source in Multilayered Media[J]. Geophysical Journal International, 2002, 148(3): 619-627 DOI:10.1046/j.1365-246X.2002.01610.x
(  0) 0) |
| [9] |
Langston C A. Seismic Ground Motions from a Bolide Shock Wave[J]. Journal of Geophysical Research: Solid Earth, 2004, 109(B12): 1-23
(  0) 0) |
| [10] |
Brocher T M. Empirical Relations between Elastic Wavespeeds and Density in the Earth's Crust[J]. Bulletin of the Seismological Society of America, 2005, 95(6): 2 081-2 092 DOI:10.1785/0120050077
(  0) 0) |
| [11] |
Prevedel B, Bulut F, Bohnhoff M, et al. Downhole Geophysical Observatories: Best Installation Practices and a Case History from Turkey[J]. International Journal of Earth Sciences, 2015, 104(6): 1 537-1 547 DOI:10.1007/s00531-015-1147-5
(  0) 0) |
2. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China;
3. Geophysical Exploration Center, CEA, 75 Wenhua Road, Zhengzhou 450002, China;
4. School of Earth and Space Science, University of Science and Technology of China, 96 Jinzhai Road, Hefei 230026, China
 2018, Vol. 38
2018, Vol. 38

