大地震、火山爆发或地下核爆炸都会引发地球整体振荡而形成驻波,即地球自由振荡。自由振荡包括球型自由振荡和环形自由振荡两种类型[1-2]。球型自由振荡包含经向运动和剪切运动,环形自由振荡只有剪切运动。地球自由振荡的频率与地球的形状、密度分布、剪切模量等存在相关性,因此研究地球自由振荡有助于了解地球内部性质、结构,改进现有模型[3-4]。此外,地球自由振荡是地震面波在传播过程中形成的驻波,其振荡的大小与震源的破裂方式和破裂长度密切相关,因此地震后的自由振荡信号可以约束地震震级和检验地震的震源机制解。
重力仪、应变仪、倾斜仪、地震仪甚至GPS阵列观测等均可记录到自由振荡模态。由于精度高、稳定性强的超导重力仪的出现,目前很多地球自由振荡的研究都是基于超导数据[5-6],但是SG数量有限,在全球范围内可用的SG只有十几台。中国大陆广泛分布有近百台垂直摆倾斜仪,且垂直摆倾斜仪对低频自由振荡信号具有较强的响应能力,而利用倾斜仪观测数据探测自由振荡的研究较少,目前只有单台观测的使用。
2011-03-11 05:46日本东北部发生MW9.0特大地震,很多学者对其激发的地球自由振荡进行研究。栾威等[7]利用单台垂直摆倾斜仪观测数据检测大地震激发的基本球型振荡(0S2~0S38)15个谐频振型以及少量环型振荡振型。姚佳骏等[8]利用重力观测资料, 检测到地震激发的0S0~0S40之间的球型自由振荡。本文首次基于中国大陆倾斜台网多台垂直摆倾斜仪观测数据进一步对该地震激发的自由振荡进行检测,研究多台资料检测自由振荡的优势,并与地震仪的检测结果进行比较,验证垂直摆倾斜仪对低频自由振荡信号的检测能力。
1 数据与处理方法2011年日本MW9.0大地震发生后,中国大陆所有垂直摆倾斜仪都记录到这次地震的同震信号。选取其中完整度较高、观测良好的36个台站的数据进行研究(考虑到观测的EW分量普遍优于NS分量,本文只使用EW分量)。36个观测量均为VS/VP型垂直摆,采样间隔为60 s,数据完整度达到99%以上,台站分布如图 1所示。

|
图 1 36个台站分布 Fig. 1 Distribution of 36 selected station |
根据Rosat等[9]的研究结果,选取震后5 h作为自由振荡检测的起始时间。数据长度越长,自由振荡信号的衰减越多,使得背景噪声的能量更加凸显,导致整体的信噪比降低;而某些模态之间的频率间隔太小,要清晰地将这些模态分辨出来,数据长度需要满足[10]:
| $ T = N \cdot \Delta t = 1/(\Delta \omega ) $ | (1) |
式中,N为采样点数,Δt为采样间隔,Δω为最小频率间隔。
综合考虑频率分辨率和信噪比的因素,选择2011-03-11 09:46后65 h的观测资料(时间长度基本上可以满足所要探测的模态分辨间隔)。就检测地震激发的地球振荡信号而言,观测资料包含仪器自身噪声、外界干扰、大气压和固体潮等信号。预处理主要为固体潮改正(大气压的变化对应变仪和倾斜仪观测影响很小,故未作改正)。去除固体潮时,考虑到使用模型法去除固体潮后,在相应的频段仍有其他噪声,使用Daubechies wavelet(db4)滤波器进行滤波处理。经过固体潮滤波之后,基本上可以全部去除长周期的固体潮分量,残差信号如图 2所示,纵坐标表示震中到台站的距离。

|
图 2 36个台站观测到的日本MW9.0大地震发生5 h后65 h的数据 Fig. 2 65 h data of tiltmeter after 5 h after the MW9.0 Tohoku earthquake at 36 stations |
目前常用的地球自由振荡功率谱分析方法大致分为两类,一类是基于传统的傅里叶变换的方法;另一类则不基于FFT,如AR(autoregressive estimation)方法[11]、MSHS(matrix-spherical harmonic stacking)[12]。一般而言,在AR谱估计检测到的信号均可在傅氏谱中检测出,且该方法不提供关于振幅的信息[13],因此本文使用傅里叶变换方法进行谱分析。考虑到一些振型只被某些台站所检测到(即每个台站的检测谱峰不完整),或是某些振型的SNR比较低,将36个台站的数据利用FFT得到的功率谱进行叠积操作,以增强信号、提高信噪比,从而使一些很微弱的振型也被检测到,达到谱峰的完整性。
| $ P(\omega ) = {\left[{\prod\limits_{i = 1}^n {S(\omega )} } \right]^{\frac{1}{N}}} $ | (2) |
式中,N为台站数量,i为台站编号,S(ω)为每个台站的谱估计值。
2 结果与讨论 2.1 地球自由振荡的检测将36个台站的数据进行傅里叶变换(加汉宁窗),得到各个台站数据在0.3~4.6 mHz频段内的功率谱,将其分为0.3~2.5 mHz和2.5~4.6 mHz两段(分别选取不同的时间长度)。图 3为36个台站数据的功率谱(0~4.6 mHz)。为增强信号提高信噪比,将36组谱分析结果作叠积,结果如图 4所示,图中黑实线表示观测结果,垂直虚线表示PREM模型理论值。图 4清晰地显示了被检测到的振型,包括0S3~0S38全部球型振荡振型、0T3~0T28几乎所有的环型振荡振型和21个谐频振型。
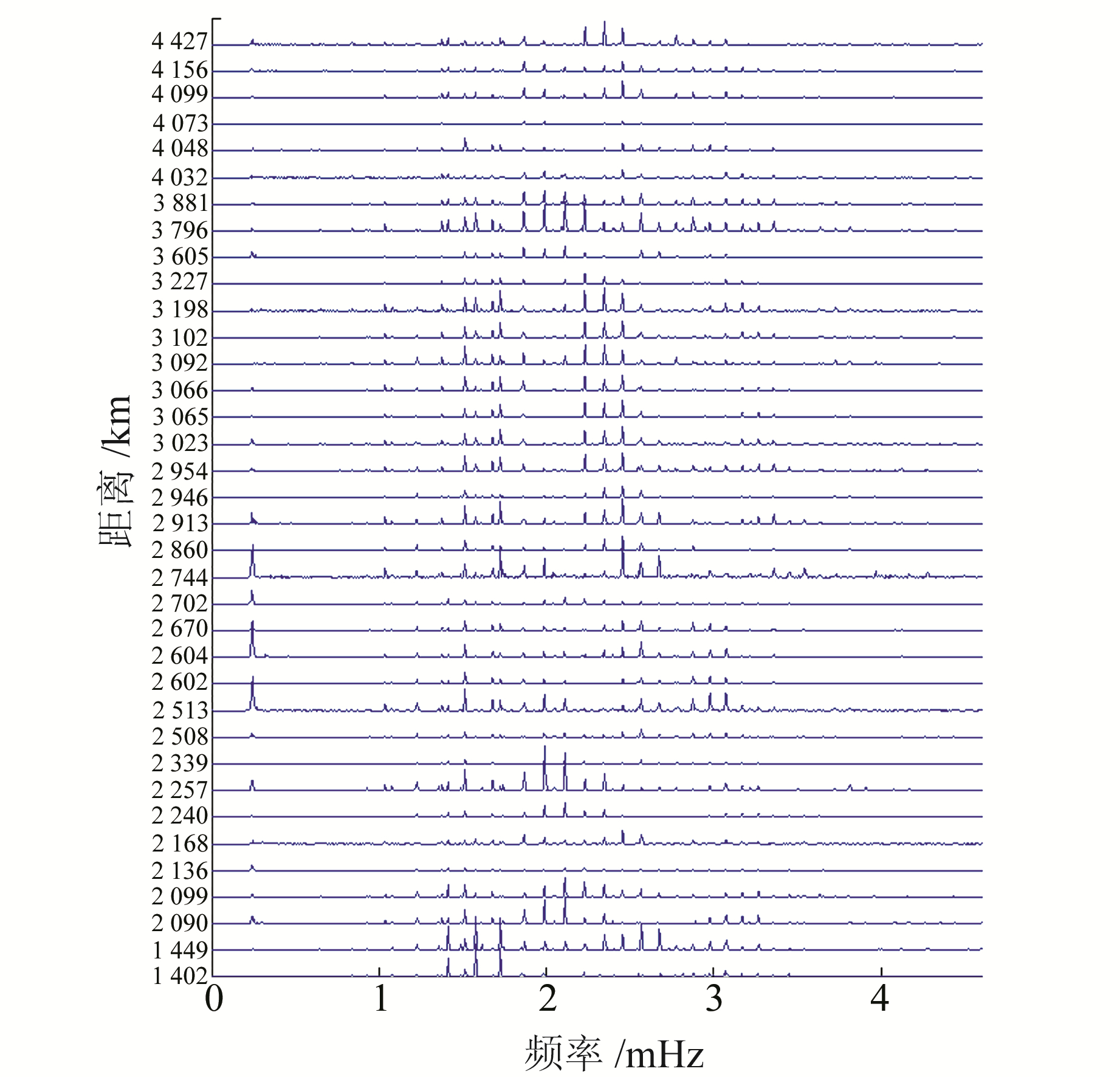
|
图 3 36个台站检测到的自由振荡信号 Fig. 3 Power spectrum of Earth's free oscillation modes detected by the tiltmeters at 36 stations |
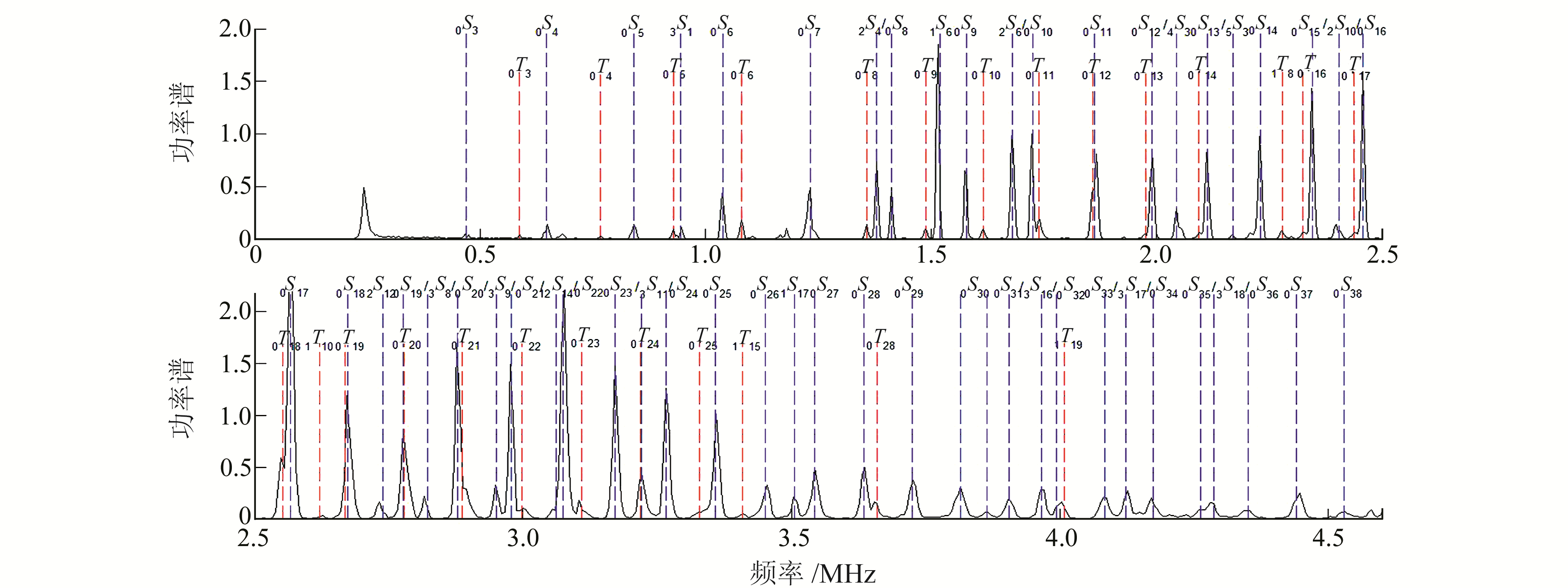
|
图 4 36个台站的积谱 Fig. 4 Product spectrum from the 36 stations |
将03-01 00:00开始的65 h的观测资料去除固体潮后的残差近似作为背景观测噪声,将残差值作傅氏变换得到背景噪声的功率谱。图 5为自由振荡信号和背景噪声的对比,红线表示背景噪声谱,蓝线表示地球自由振荡信号谱。可以看出,绝大部分的检测结果具有较高的信噪比(除一些超低频的振型如0S3、0T3、0T4),说明检测结果可靠。
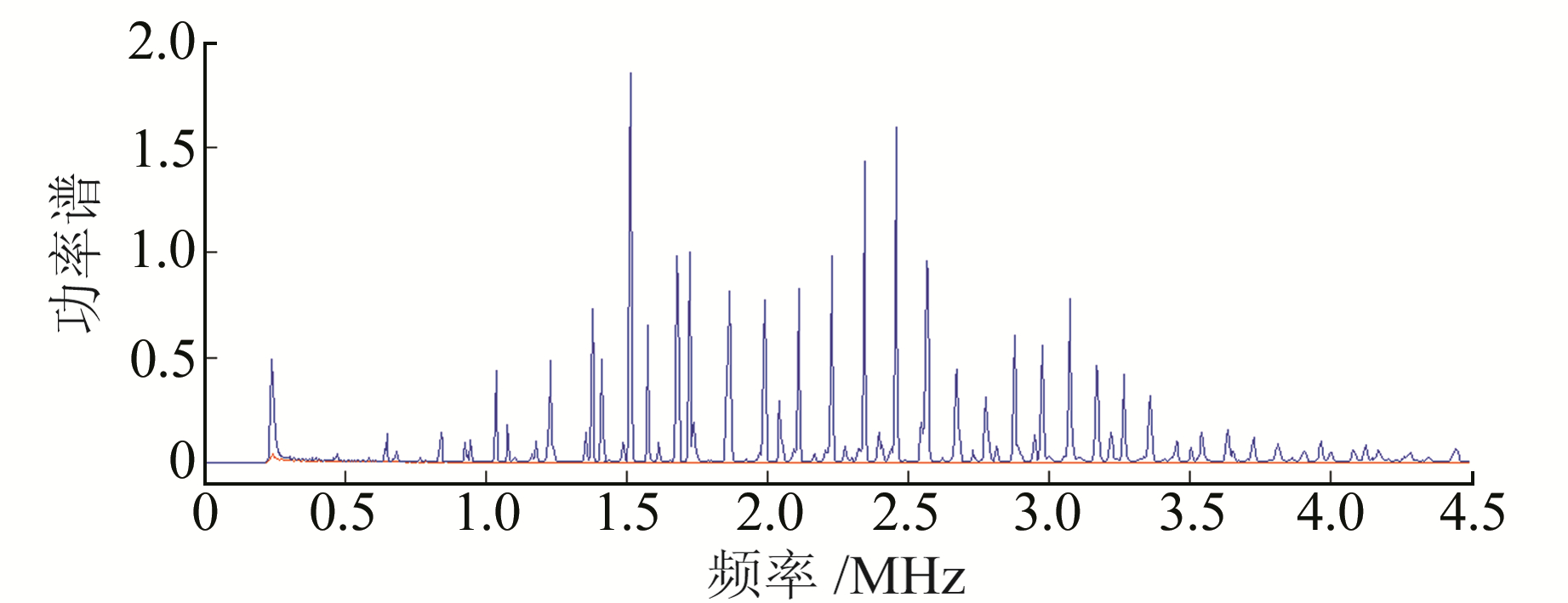
|
图 5 噪声谱与自由振荡信号谱对比 Fig. 5 Comparison of power spectrum before and after the Tohoku MW9.0 earthquake |
根据功率谱密度的结果, 统计检测到的自由振荡振型的频率值,并将结果与PREM模型理论值进行对比,表 1是基频球型振荡的统计结果。可以看出,0S10、0S16、0S17、0S19、0S22、0S23、0S24共7个振型的观测频率与理论值的偏差近似为0。另外,绝大多数的振型观测频率与理论值偏差在0.1%以内,总体偏差为0.09%。表 2是基频环型振荡的统计结果。可以看出,绝大多数的振型观测频率与理论值偏差在0.1%以内,总体偏差为0.08%。表 3是谐频振荡的统计结果。可以看出,总体偏差为0.1%。图 6为检测到的振型的偏差分布。
|
|
表 1 本文基频球型自由振荡观测值与PREM模型理论值及其偏差 Tab. 1 Differences between observed values in this paper and the theoretical values of PREM on spheroidal normal modes |
|
|
表 2 本文基频环型自由振荡观测值与PREM模型理论值及其偏差 Tab. 2 Differences between observed values in this paper and the theoretical values of PREM on toroidal normal modes |
|
|
表 3 本文谐频自由振荡观测值与PREM模型理论值及其偏差 Tab. 3 Differences between observed values in this paper and the theoretical values of PREM on harmonic normal modes |
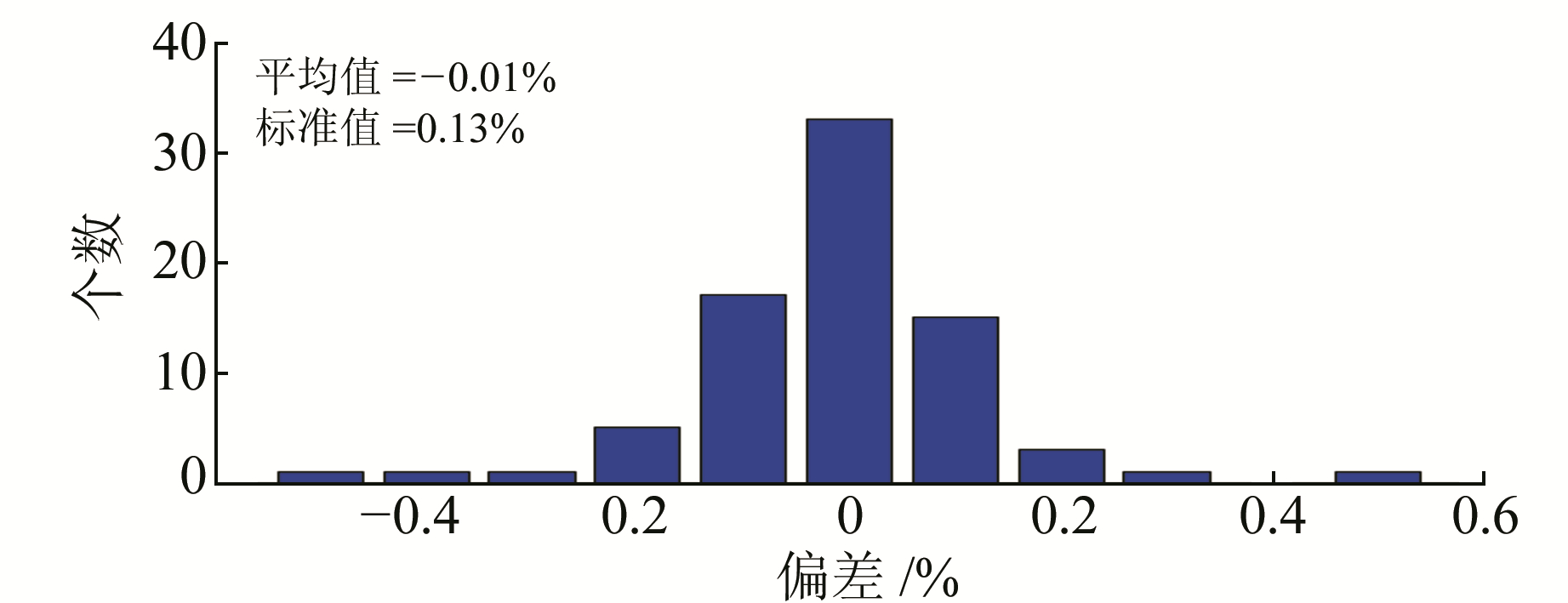
|
图 6 检测到的振型偏差分布 Fig. 6 The distribution of relative error of different modes detected by tiltmeters from 36 stations |
与单台站相比,多台站叠积的方法不仅能增强信号、提高信噪比, 使一些微弱的信号被检测到,且能使观测到的谱峰更加完整。本文检测到了1T8、1T10、1T15、1T19共4个谐频环型振荡,在已发表的成果中,还没有用倾斜仪资料检测到谐频环型振荡。与文献[7]相比,本文还检测到更多的谐频球型振荡振型。
本文未能检测到高于4.5 mHz频段的振型,第一种可能是随着振荡频率增加,衰减变快;第二种可能是受仪器本身采样率的限制。此外,某些简正模之间频率间隔太小,以至于未能将其分开,如0S18~0T19和0S19~0T20。
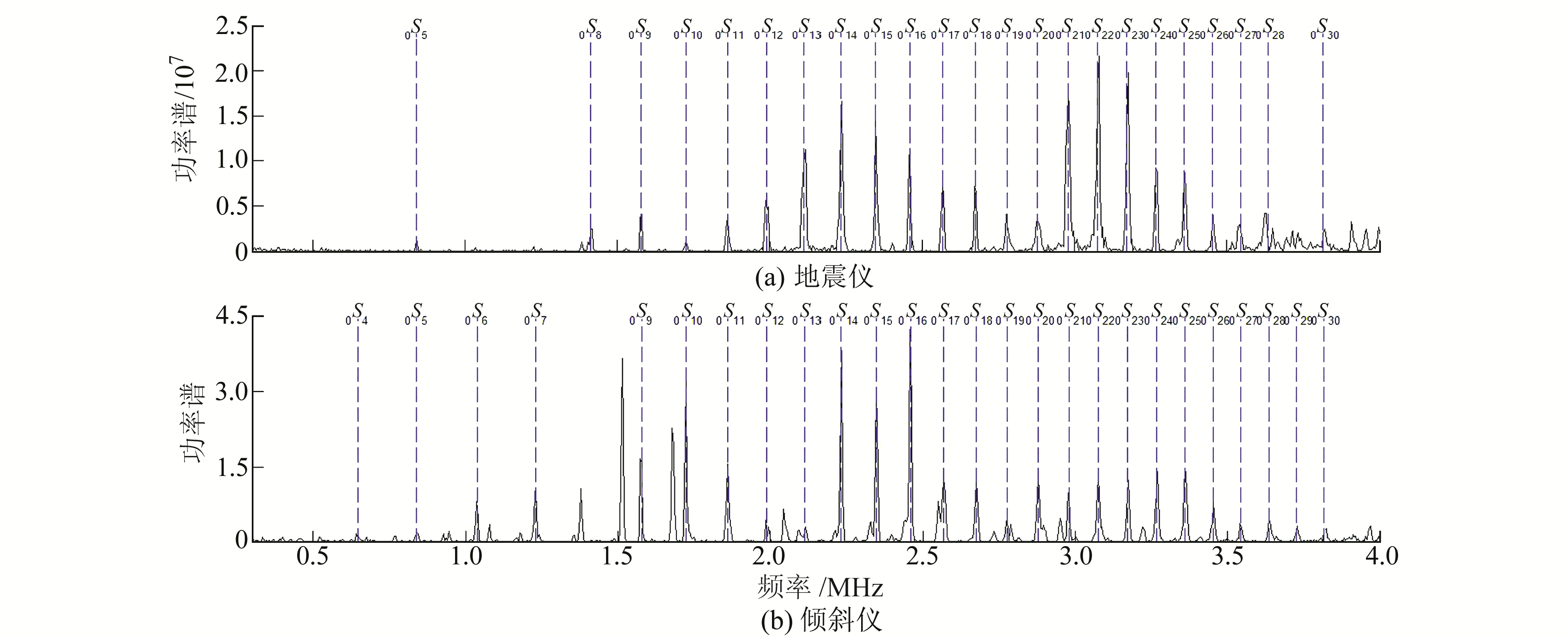
2.2 地震仪与垂直摆倾斜仪的比较选取宜昌台垂直摆倾斜仪和地震仪观测资料进行分析。考虑到倾斜仪观测的是地壳相对于铅垂线的偏移,主要得到的是垂直方向的相对位移,选择地震仪观测的Z分量进行研究。此外,为使二者的采样率相同,对地震仪观测数据进行重新采样(60 s)。选取地震发生5 h后的65 h的数据,同样使用Daubechies wavelet(db4)滤波器进行滤波处理,利用傅里叶变换得到功率谱,结果如图 7所示。
|
图 7 宜昌台垂直摆倾斜仪与宽频地震仪检测结果对比 Fig. 7 Comparison between the power spectra of seismograms and the tilemeter at Yichang station |
由图 7可知,在相对高频段(1.5~4 mHz),地震仪和垂直摆倾斜仪检测到的振型都具有较强的信号。但在 < 1.5 mHz频段,地震仪信号很弱,而垂直摆倾斜仪仍具有较强的检测能力。此外,垂直摆倾斜仪能检测到一些地震仪未能检测到的非常微弱的振型,如0S7、0S6、0S4。因此,对于超低频段的自由振荡振型检测,垂直摆倾斜仪要比宽频地震仪具有更强的检测能力。
3 结语本文使用分布在中国大陆的36台垂直摆倾斜仪观测数据,检测2011日本MW9.0大地震激发的地球自由振荡。检测到了0S3~0S38全部基频球型振荡,0T3~0T28几乎所有基频环型振荡振型,此外还有21个谐频振型。各个振型观测频率与PREM模型理论值基本一致,垂直摆倾斜仪在检测自由振荡信号方面效果明显,特别是经过多台叠积后,有更多的振型被检测到,信噪比更高。
垂直摆倾斜仪对低频段自由振荡观测能力优势明显,尤其是在1~4 mHz频段内具有很高的信噪比,与地震仪相比,在超低频段(< 1.5 mHz)的观测能力要更优一些。
使用多台站数据叠积的方法在提高信噪比、探测一些微弱振型、提高谱峰完整度等方面具有一定作用,相比于单台数据,能够检测到更多的谐频振型。
| [1] |
Ness N F, Harrison J C, Slichter L B. Observations of the Free Oscillations of the Earth[J]. Journal of Geophysical Research, 1961, 66(2): 621-629 DOI:10.1029/JZ066i002p00621
(  0) 0) |
| [2] |
Alterman Z S, Eyal Y, Merzer A M. On Free Oscillations of the Earth[J]. Geophysical Surveys, 1974, 1(4): 409-428 DOI:10.1007/BF01452247
(  0) 0) |
| [3] |
Resovsky J S, Ritzwoller M H. New and Refined Constraints on Three-Dimensional Earth Structure from Normal Modes below 3 mHz[J]. Journal of Geophysical Research:Atmospheres, 1998, 103(B1): 783-810 DOI:10.1029/97JB02482
(  0) 0) |
| [4] |
Park J, Song T R, Tromp J, et al. Earth's Free Oscillations Excited by the 26 December 2004 Sumatra-Andaman Earthquake[J]. Science, 2005, 308(5 725): 1 139-1 144
(  0) 0) |
| [5] |
Camp M V. Measuring Seismic Normal Modes with the GWR C021 Superconducting Gravimeter[J]. Physics of the Earth & Planetary Interiors, 1999, 116(1): 81-92
(  0) 0) |
| [6] |
雷湘鄂, 许厚泽, 孙和平. 由5个国际超导重力仪台站资料检测到的秘鲁8.2级大地震所激发的球型自由振荡现象[J]. 中国科学:地球科学, 2004, 34(5): 483-491 (Lei Xiang'e, Xu Houze, Sun Heping. Detection of Spheriodal Free Oscillation Excited by Peru MS8.2 Earthquake with Five International Superconducting Gravimeter Data[J]. Scinece China Earth Science, 2004, 34(5): 483-491)
(  0) 0) |
| [7] |
栾威, 申文斌, 贾剑钢. 利用VP型垂直摆倾斜仪观测数据检测2011日本MW9.0级地震激发的低频地球自由振荡[J]. 地球物理学报, 2015, 58(3): 844-856 (Luan Wei, Shen Wenbin, Jia Jiangang. Detection of Low-Frequency Modes of Earth's Free Oscillation Excited by the Japan MW9.0 Earthquake Using Observations of the Vertical Pendulum Tiltmeter[J]. Chinese Journal of Geophysics, 2015, 58(3): 844-856 DOI:10.6038/cjg20150314)
(  0) 0) |
| [8] |
姚家骏, 万永革, 王培玲, 等. 利用重力资料检测日本9.0级地震激发的地球自由振荡[J]. 地震研究, 2012, 35(1): 53-58 (Yao Jiajun, Wan Yongge, Wang Peiling, et al. Detecting the Free Oscillations of the Earth Excited by the Japan M9.0 Earthquake Using Gravity Observation Data[J]. Journal of Seismological Research, 2012, 35(1): 53-58)
(  0) 0) |
| [9] |
Rosat S, Sato T, Imanishi Y, et al. Correction to "High-Resolution Analysis of the Gravest Seismic Normal Modes after the 2004 MW=9 Sumatra Earthquake Using Superconducting Gravimeter Data"[J]. Geophysical Research Letters, 2006, 39(22)
(  0) 0) |
| [10] |
丁浩, 申文斌. 探测一阶模态三重分裂的MSE技术和SHS方法的比较研究[J]. 地球物理学报, 2013, 56(10): 3 313-3 323 (Ding Hao, Shen Wenbin. Comparative Study of the MSE Technique and SHS Method Used for Detection of nS1 Mode Triplet[J]. Chinese Journal of Geophysics, 2013, 56(10): 3 313-3 323)
(  0) 0) |
| [11] |
Chao B F, Gilbert F. Autoregressive Estimation of Complex Eigenfrequencies in Low Frequency Seismic Spectra[J]. Geophysical Journal of the Royal Astronomical Society, 1980, 63(3): 641--657 DOI:10.1111/gji.1980.63.issue-3
(  0) 0) |
| [12] |
Ding H, Chao B F. Data Stacking Methods for Isolation of Normal-Mode Singlets of Earth's Free Oscillation: Extensions, Comparisons, and Applications[J]. Journal of Geophysical Research:Solid Earth, 2015, 120(7): 5 034-5 050 DOI:10.1002/2015JB012025
(  0) 0) |
| [13] |
Chao B F. Comment on "A New Nethod of Spectral Analysis and Its Application to the Earth's Free Oscillations: The 'Sompi' Method" by S. Hori et al[J]. Journal of Geophysical Research:Atmospheres, 1990, 95(B12): 19789-19790 DOI:10.1029/JB095iB12p19789
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38


