2. 西南交通大学地球科学与环境工程学院,成都市高新区西部园区,611756
海潮负荷效应(ocean tide loading, OTL)建模通常采用全球海潮模型和格林函数褶积积分的方法,其建模的精度在很大程度上取决于海潮模型的精度[1]。不同全球海潮模型的M2潮波振幅在某些地区的RMS差异可达8 mm[2];基于不同海潮模型建模得到的OTL位移U分量差异可达20%[3];同一海潮模型选取的潮波数不同也会导致OTL位移改正数mm级的差异[4]。实际上,目前还不存在对地球上任何区域都有最佳解算结果的海潮模型,因此全球尺度的海潮负荷研究往往需要结合不同的海潮模型[5]。对于中国区域的OTL位移建模,不同海潮模型造成的渤海、东海和南海沿岸的系统性差异可达数mm,其差异主要源于海潮模型近场或远场区域之间的差异[6]。
本文利用较长的GNSS坐标时间序列分析评估4种海潮模型在中国沿海各区域的改正效果,首先比较不同海潮模型潮波参数的区域性差异,然后讨论不同海潮模型对OTL改正前后坐标时间序列wRMS的影响,为选取中国沿海海潮负荷改正模型提供参考价值。
1 数据 1.1 海潮模型海潮模型通常利用海潮观测数据或卫星测高数据进行经验分析得到,或在流体动力学模型基础上同化各类观测数据构建而成,其中后者占绝大部分。另外,由于海岸线复杂、海底构造特殊,海潮模型在近海区域精度有限已成为共识。
本文选取的海潮模型包括FES2004、EOT11a、TPXO7.2和Chinasea2010。FES2004和TPXO7.2模型基于流体动力学模型,同化了潮汐测量数据和卫星测高数据,TPXO7.2模型还包括极地区域的观测数据,这2个模型均为IERS规范2010推荐使用的模型。EOT11a模型是一组经验模型,通过对卫星测高数据的经验分析得到,并与全球范围内56个沿海验潮站数据比较符合[7],可用于对FES2004模型的改正。Chinasea2010模型应用中国南海、台湾海峡及泰国湾等沿岸和岛屿55个沿海验潮站资料及卫星测高数据,潮位精度较高,区域范围为99°~129°E,1°~41°N。表 1给出了以上模型的基本情况。
|
|
表 1 海潮模型信息 Tab. 1 Info of ocean tide models |
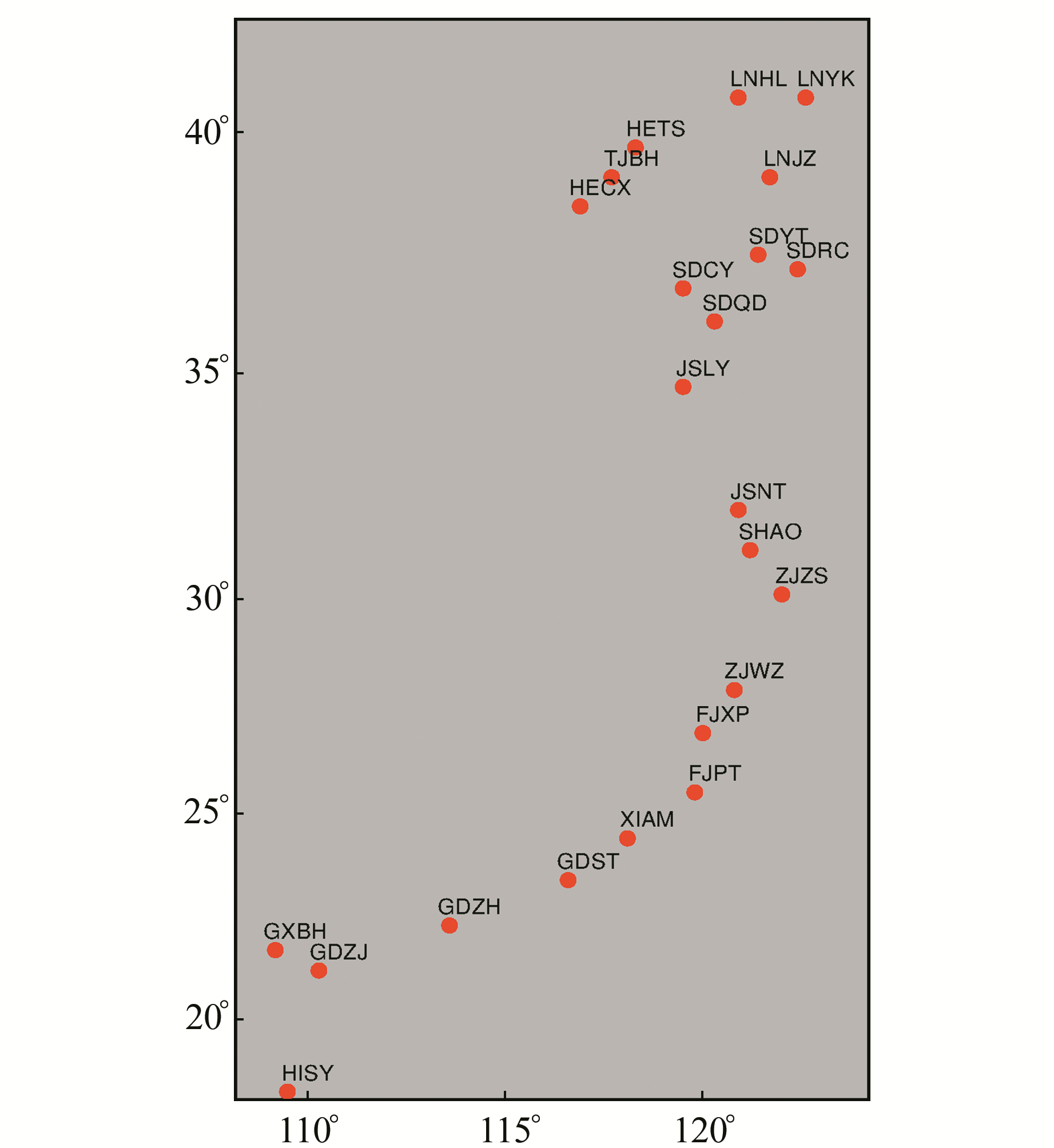
选取中国大陆构造环境监测网络(crustal movement observation network of China, CMONOC)发布的沿海区域23个测站的观测数据进行分析。选取的测站均位于海岸线200 km以内区域且数据质量良好,测站分布见图 1。23个测站的坐标时间序列均为ITRF框架下的GNSS单日解,序列跨度为2010~2016年,且已去除趋势项。
|
图 1 测站分布 Fig. 1 Distribution of the stations |
OTL位移建模实质是通过叠加各分潮波的影响得到总负荷位移,包括半日潮波M2、S2、N2和K2,周日潮波K1、O1、P1和Q1,长周期潮波Mm、Mf和Ssa。海潮模型提供各个分潮波参数(振幅和相位)。各海潮模型的建模差异直接体现在所得分潮波参数的不同,可利用矢量差进行评价。
用A1、φ1、A2、φ2表示2个不同海潮模型分别计算得到的OTL位移振幅和格林尼治相位延迟,矢量差计算公式为:
| $ \begin{array}{l} d = \\ \sqrt {{{\left( {{A_1}\cos {\varphi _1}-{A_2}\cos {\varphi _2}} \right)}^2} + {{\left( {{A_1}\sin {\varphi _1}-{A_2}\sin {\varphi _2}} \right)}^2}} \end{array} $ | (1) |
IERS2010规范中,尽管推荐使用FES2004海潮模型进行OTL改正,但其他模型可能有更佳的内符合精度[12]。因此本文以FES2004模型为参考,分析其他海潮模型的潮波参数与其差异。利用SPOTL软件[13]和Bos-Scherneck网站[14]分别计算EOT11a、TPXO7.2、Chinasea2010及FES2004等4种海潮模型在中国沿海区域(18~42.3°N,108~124.2°E)各分潮波3个分量的振幅和相位,格网间隔为0.25°×0.25°。根据式(1)将EOT11a、TPXO7.2和Chinasea2010模型所得潮波参数分别与FES2004模型所得参数作矢量差运算。
2.2 GNSS坐标时间序列OTL改正由于CMONOC发布的数据成果已经进行了基于FES2004全球海潮模型的OTL改正,首先将该项改正还原,然后分别采用EOT11a、TPXO7.2和Chinasea2010模型进行重新改正。
测站OTL位移的3个分量ΔCk(k=1, 2, 3分别代表E、N和U分量)可通过累加各潮波分别造成的位移进行计算:
| $ \Delta {C_k} = \sum\limits_{j = 1}^n {{f_i}{A_{k, j}}\cos \left( {{\omega _j}t + {\chi _j}\left( {{t_0}} \right) + {\mu _j}-{\mathit{\Phi} _{k, j}}} \right)} $ | (2) |
式中,Ak, j和Φk, j分别为潮波j在E、N和U分量(k=1, 2, 3)上的振幅和格林尼治相位,ωj和χj(t0)分别为潮波j的角频率和天文幅角初相,n为潮波数。除11个主潮波外,本文还采用IERS协议2010推荐的最新海潮改正计算方法[12],将11个主潮汐分量应用样条插值法扩展成为342个小潮波,其模型精度达到0.1%。
2.3 GNSS坐标时间序列RMS分析为了定量计算基于不同海潮模型的OTL改正对测站坐标时间序列的影响,计算不同海潮模型改正前后的序列wRMS差异[15]。改正前后(TSaf/bf)的坐标时间序列wRMS可由式(3)计算得到,由式(4)可以得到wRMS改正百分比。
| $ \begin{array}{l} {\rm{wRMS}}\left( {{\rm{T}}{{\rm{S}}_{{\rm{af}}/{\rm{bf}}}}} \right) = {\rm{sqrt}}\\ \left( {\frac{{\sum\nolimits_1^n {w\left( i \right)} {{\left( {{\rm{T}}{{\rm{S}}_{{\rm{af}}/{\rm{bf}}}}\left( i \right)-\frac{{\sum\nolimits_1^n {{\rm{T}}{{\rm{S}}_{{\rm{af}}/{\rm{bf}}}}\left( i \right)w\left( i \right)} }}{{\sum\nolimits_1^n {w\left( i \right)} }}} \right)}^2}}}{{\sum\nolimits_1^n {w\left( i \right)} }}} \right) \end{array} $ | (3) |
| $ d\% = \frac{{{\rm{wRMS}}\left( {{\rm{T}}{{\rm{S}}_{{\rm{af}}}}} \right)}}{{{\rm{wRMS}}\left( {{\rm{T}}{{\rm{S}}_{{\rm{bf}}}}} \right)}} \times 100\% $ | (4) |
式中,
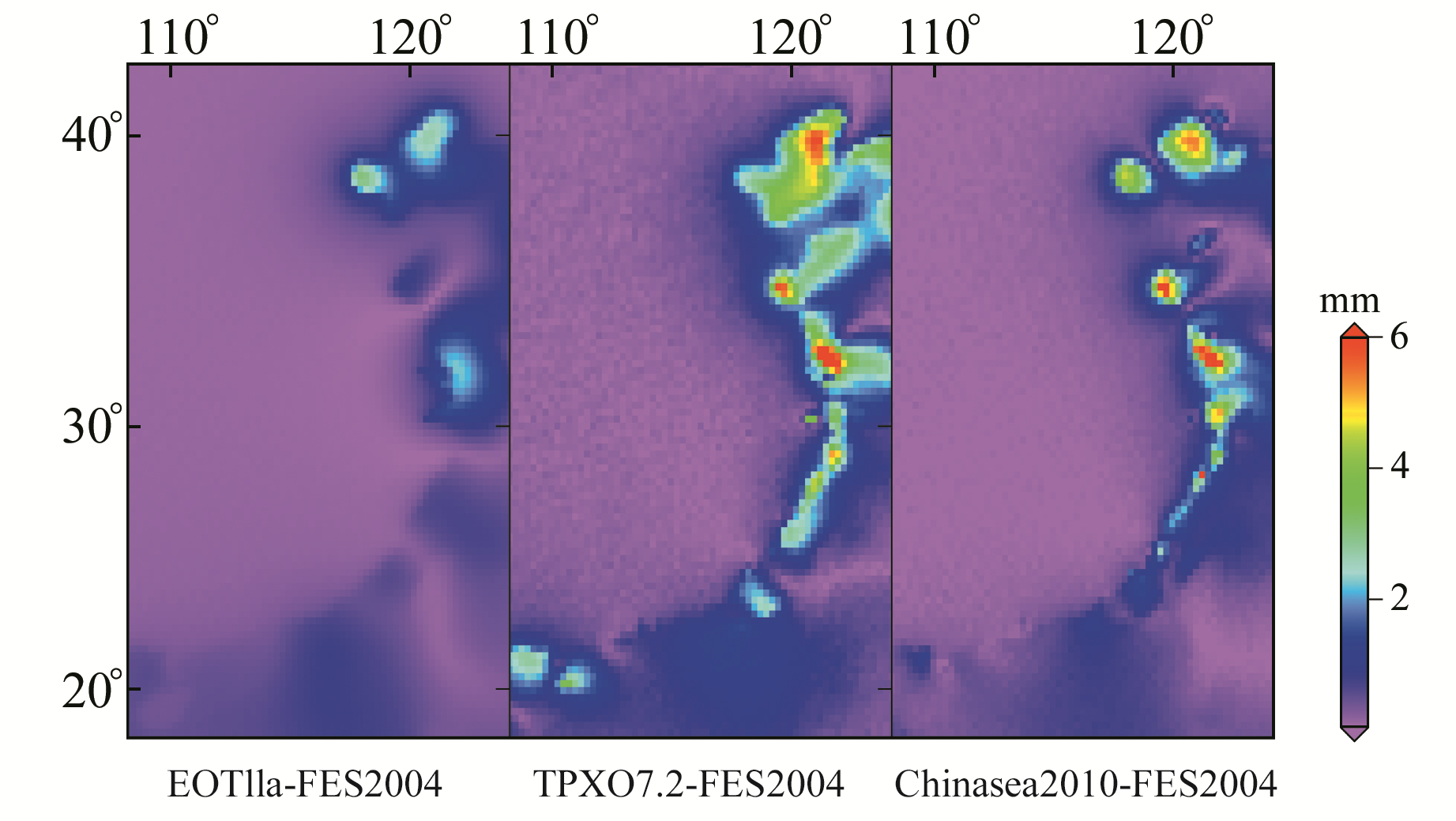
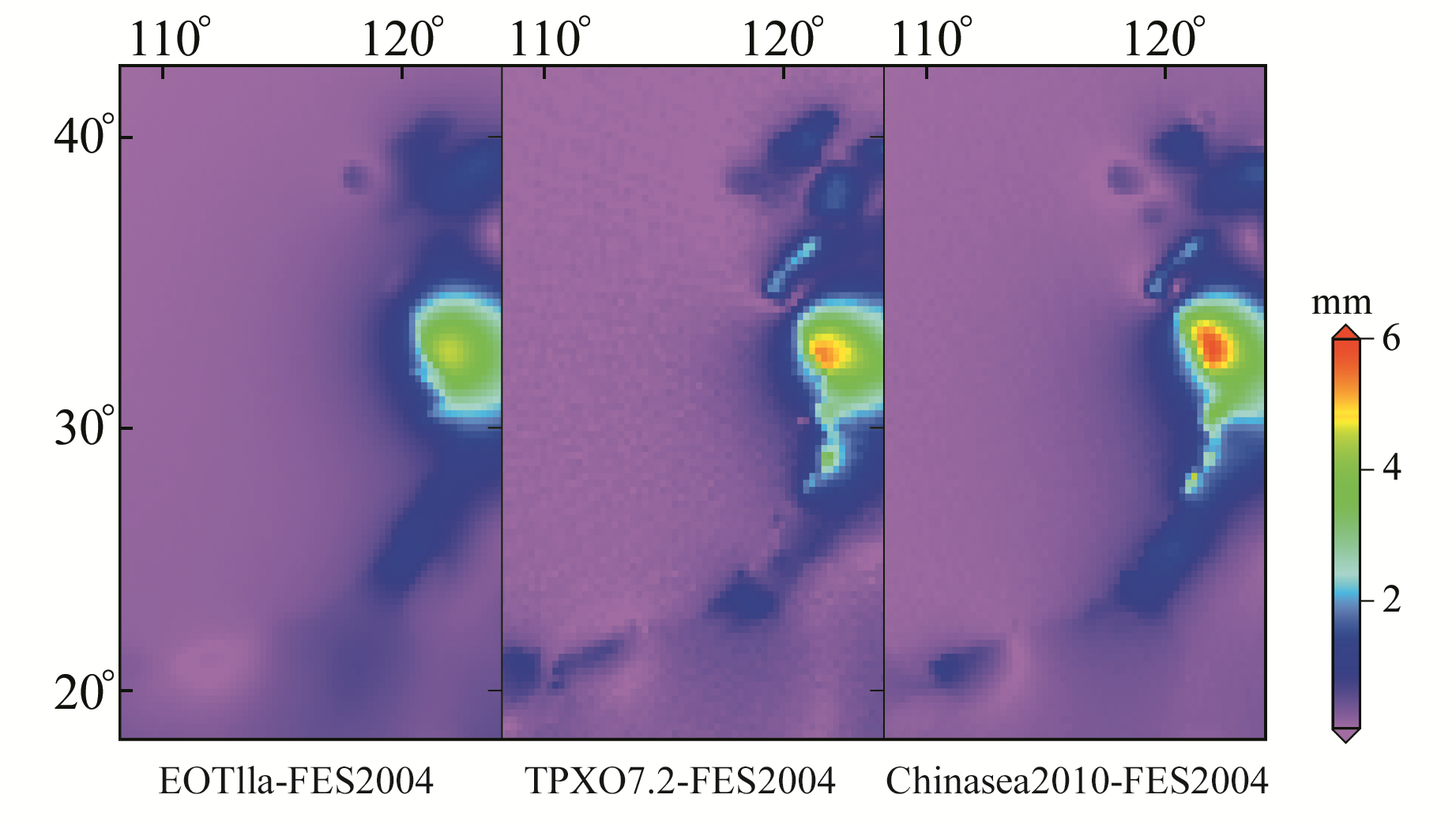
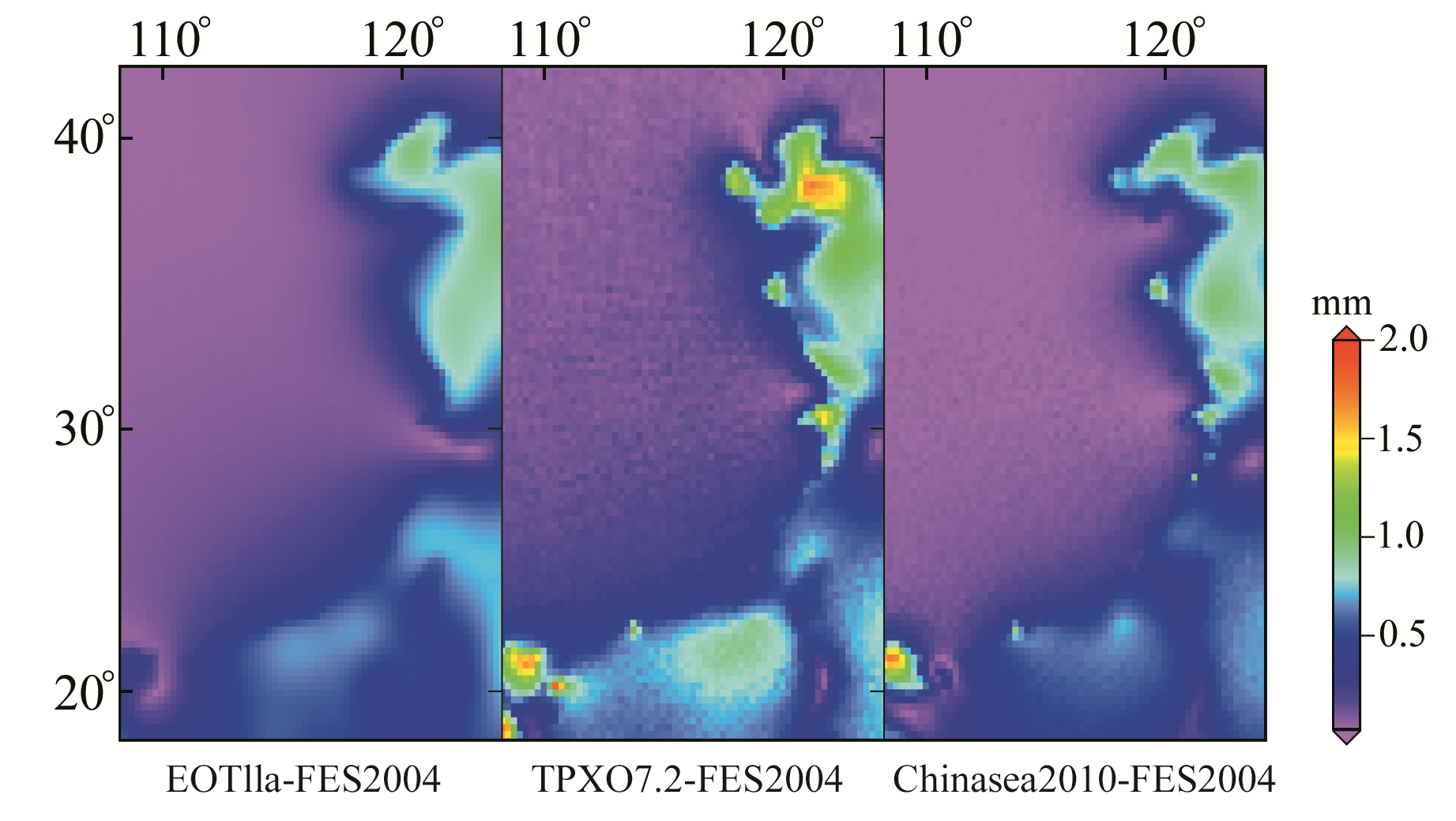
OTL引起的U分量位移比N、E分量更显著,且周日潮、半日潮呈现类似的差异形态,因此以M2、S2潮波和K1、O1潮波为例,讨论不同海潮模型得到的半日、周日潮波的U分量潮波参数差异的分布形态,如图 2~5所示。
|
图 2 M2潮波参数差异(U) Fig. 2 The discrepancy of M2 parameters (U) |
|
图 3 S2潮波建模参数差异(U) Fig. 3 The discrepancy of S2 parameters (U) |
|
图 4 K1潮波建模参数差异(U) Fig. 4 The discrepancy of K1 parameters (U) |
|
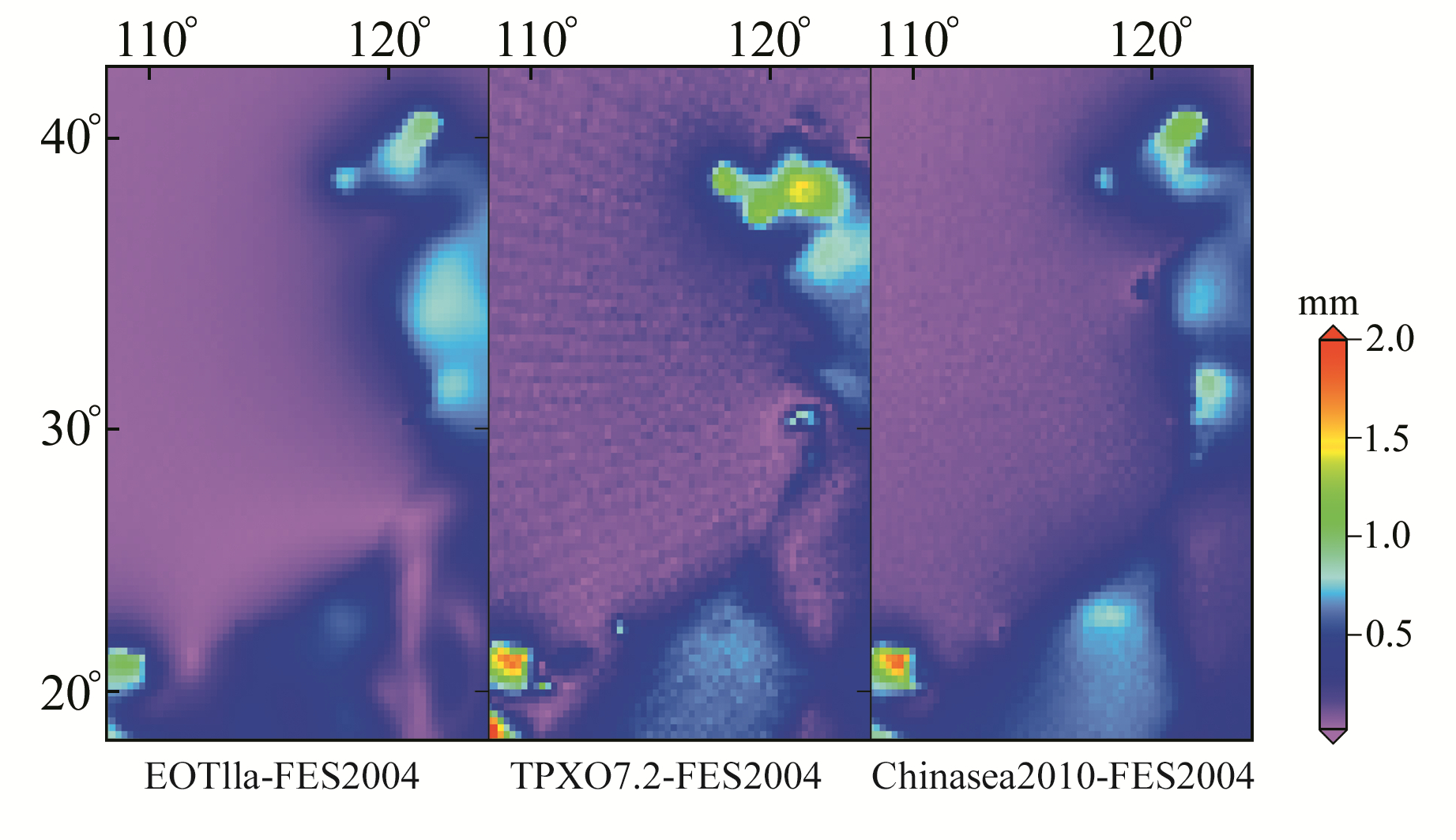
图 5 O1潮波建模参数差异(U) Fig. 5 The discrepancy of O1 parameters (U) |
由图 2看出,EOT11a和FES2004模型得到的M2潮波U分量上的参数差异(以下简称“EOT11a-FES2004差异”)在渤海西部和北部沿岸以及江苏省东南沿岸等区域最大,为1.5~1.9 mm,其他区域均在1.5 mm以下;TPXO7.2-FES2004最大差异在辽宁南部、杭州湾沿岸和江苏沿岸等区域,达4.7 mm;Chinasea2010-FES2004差异与TPXO7.2-FES2004差异分布形态类似,最大差异达4 mm以上。对于内陆区域,4种模型差异非常小。
对于S2潮波(图 3),EOT11a-FES2004、TPXO7.2-FES2004和Chinasea2010-FES2004差异呈现相同的分布形态,最大差异均在杭州湾和江苏沿海等区域,分别为3.3 mm、3.6 mm和3.5 mm。在内陆和其他沿海区域,4种模型具有良好的一致性,差异均在1.0 mm以下。
图 4为K1潮波差异的分布形态,较半日潮M2、S2有明显区别,且量级较小。EOT11a-FES2004差异在渤海沿岸、山东东部至江苏沿海等区域最大,为0.6~0.7 mm;内陆差异最小,在0.2 mm以下。TPXO7.2-FES2004差异在雷州半岛和海南北部等区域最大,为1.4 mm;其次在辽宁大连、山东蓬莱、广西北海及杭州湾等沿海区域均为1.2 mm左右;其他沿海区域为0.5~1 mm。Chinasea-FES2004最大差异达1.1 mm,分布形态与TPXO7.2-FES2004差异类似。
O1潮波(图 5)与K1潮波的差异分布形态十分类似,但最大差异所在区域不同。EOT11a-FES200的整体差异都很小,均为0.7 mm以下。TPXO7.2-FES2004和Chinasea-FES2004差异分布类似,在渤海南部、广西南部和海南省西南部等沿海区域的差异较大,为1~1.4 mm;其他地区的差异均在0.5 mm以内。
综上所述,对于中国沿海区域,EOT11a、TPXO7.2和Chinasea2010模型分别与FES2004模型所得潮波参数在U分量上的差异达mm级,且沿海区域的差异远大于内陆区域。不同海潮模型所得潮波参数的差异体现出海潮模型对中国沿海区域OTL位移建模有较大的影响。
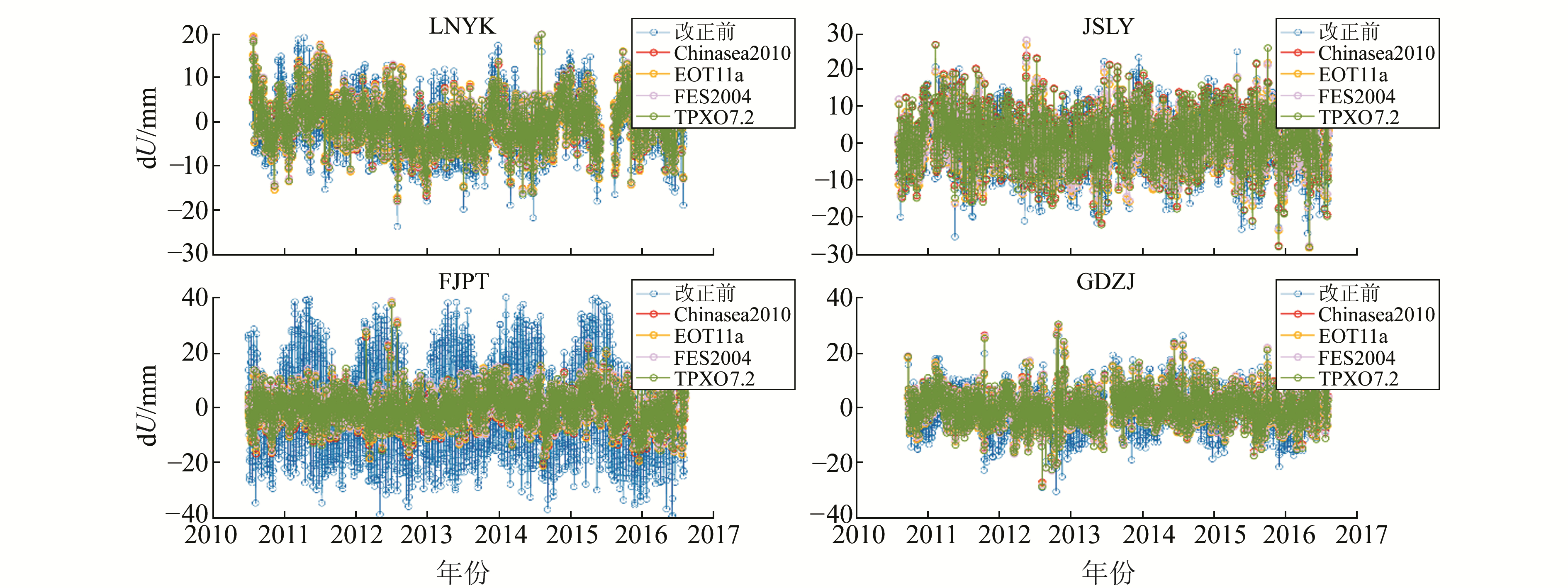
3.2 时间序列OTL改正以LNYK、JSLY、FJPT和GDZJ等4个测站为例,4种模型改正前和改正后的序列如图 6所示。渤海、黄海、东海和南海沿海区域其他测站的时间序列分别与这4个测站类似。
|
图 6 基于4种海潮模型进行OTL改正前后的测站时间序列 Fig. 6 Coordinate time series of stations before and after OTL correction based on four ocean tide models |
从图 6看出,这4个测站基于4种海潮模型的OTL改正效果相近。
3.3 wRMS分析表 2给出了各测站坐标时间序列在OTL改正前和利用不同海潮模型进行OTL改正后的wRMS及其改正百分比(图 7)。
|
|
表 2 wRMS及改正百分比 Tab. 2 wRMS and wRMS difference |
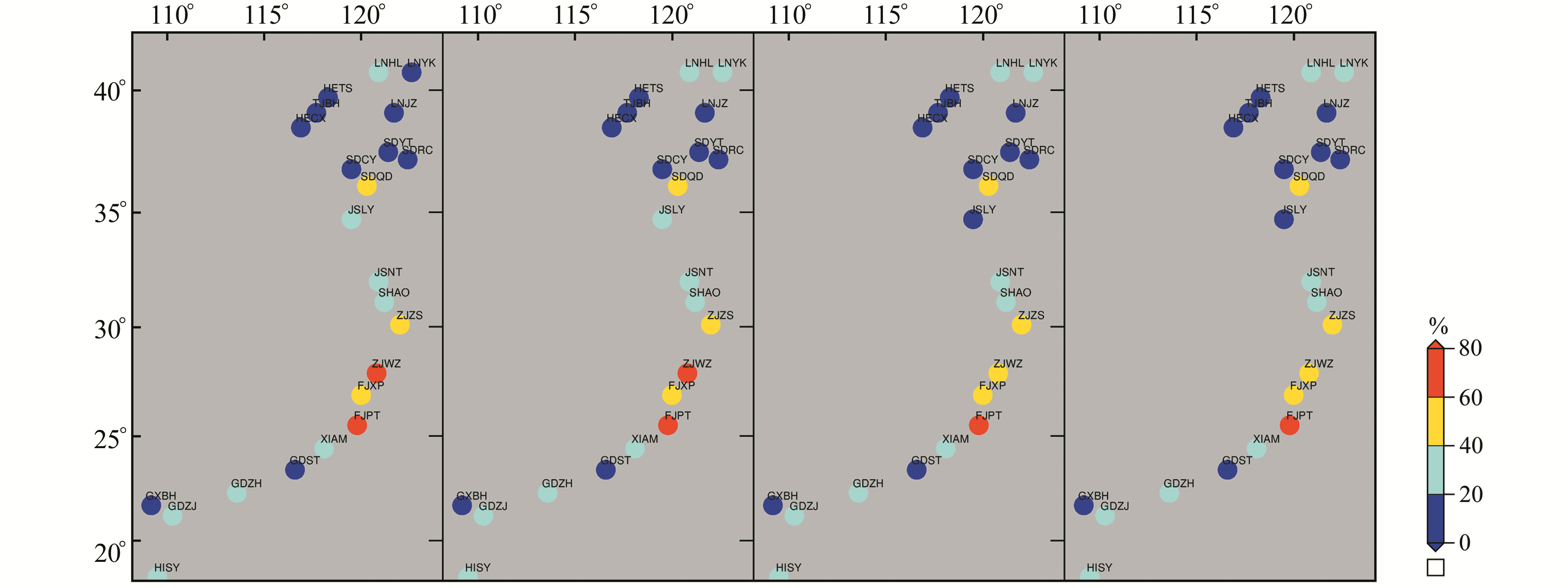
|
图 7 wRMS减小百分比分布 Fig. 7 Distribution of wRMS difference |
从表 2和图 7可以看出,OTL改正对中国沿海区域坐标时间序列wRMS的影响幅度为10%~70%。利用FES2004、EOT11a和TPXO7.2模型进行OTL改正对坐标时间序列wRMS的影响相近,模型间差异为1%~2%,其中FES2004模型对序列wRMS的影响最大。另一方面,OTL改正对坐标时间序列wRMS的影响与测站所在区域有关,东海沿岸测站序列wRMS的减小幅度最显著,达50%左右;南海沿岸和黄海沿岸测站序列wRMS减小幅度为20%~40%;渤海沿岸测站序列wRMS减小幅度最小,均在20%以下。
4 结语1) 4种模型的潮波参数存在mm级差异,沿海区域差异远比内陆显著。其中M2潮波TPXO7.2-FES2004的差异可达4.7 mm。海潮模型的选取对中国沿海区域测站的OTL改正具有较大影响。
2) 基于4种模型的改正结果相近,wRMS改正百分比差异为1%~2%。OTL改正对坐标时间序列wRMS的影响因区域而异,中国沿海区域测站的wRMS减小幅度为10~70%,东海沿岸测站wRMS的改善最为显著,可减小50%以上,可认为东海沿岸区域海潮模型的精度更高。
| [1] |
Bos M S, Baker T F. An Estimate of the Errors in Gravity Ocean Tide Loading Computations[J]. Journal of Geodesy, 2005, 79(1): 50-63
(  0) 0) |
| [2] |
Penna N T, King M A, Stewart M P. GPS Height Time Series: Short-Period Origins of Spurious Long-Period Signals[J]. Journal of Geophysical Research, 2007, 112(B2): 1074-1086
(  0) 0) |
| [3] |
Penna N T, Bos M S, Baker T F, et al. Assessing the Accuracy of Predicted Ocean Tide Loading Displacement Values[J]. Journal of Geodesy, 2008, 82(12): 893-907 DOI:10.1007/s00190-008-0220-2
(  0) 0) |
| [4] |
陈宪冬. GPS精密定位中的海潮负荷改正[J]. 西南交通大学学报, 2006, 41(4): 429-432 (Chen Xiandong. Ocean Tide Loading Corrections in GPS Precise Positioning[J]. Journal of Southwest Jiaotong University, 2006, 41(4): 429-432)
(  0) 0) |
| [5] |
Baker T F, Bos M S. Validating Earth and Ocean Tide Models Using Tidal Gravity Measurements[J]. Geophysical Journal International, 2003, 152(2): 468-485 DOI:10.1046/j.1365-246X.2003.01863.x
(  0) 0) |
| [6] |
由晓文. 中国沿海地区海潮负荷位移建模[D]. 成都: 西南交通大学, 2016 (You Xiaowen. The Modeling of Ocean Tide Loading Displacements in the Coastal Area of China[D]. Chengdu: Southwest Jiaotong University, 2016) http://cdmd.cnki.com.cn/Article/CDMD-10613-1016154987.htm
(  0) 0) |
| [7] |
Stammer D, Ray R D, Andersen O B, et al. Accuracy Assessment of Global Barotropic Ocean Tide Models[J]. Reviews of Geophysics, 2014, 52(3): 243-282 DOI:10.1002/2014RG000450
(  0) 0) |
| [8] |
Lyard F, Lefevre F, Letellier T, et al. Modelling the Global Ocean Tides: Modern Insights from FES2004[J]. Ocean Dynamics, 2006, 56(5): 394-415
(  0) 0) |
| [9] |
Savcenko R, Bosch W, Dettmering D, et al. EOT11a-Global Empirical Ocean Tide Model from Multi-Mission Satellite Altimetry, with Links to Model Results[R]. Deutsches Geodätisches Forschungsinstitut, München, 2012
(  0) 0) |
| [10] |
Egbert G D, Erofeeva S Y. Efficient Inverse Modeling of Barotropic Ocean Tides[J]. Journal of Atmospheric & Oceanic Technology, 2002, 19(2): 183-204
(  0) 0) |
| [11] |
赵大江, 郭春喜, 张世娟, 等. 中国沿海不同海潮模型的倾斜负荷分析[J]. 大地测量与地球动力学, 2015, 35(1): 34-39 (Zhao Dajiang, Guo Chunxi, Zhang Shijuan, et al. Analysis of Tilt Loading with Different Ocean Tide Models in Coastal Area of China[J]. Journal of Geodesy and Geodynamics, 2015, 35(1): 34-39)
(  0) 0) |
| [12] |
Petit G, Luzum B. IERS Conventions (2010)[R]. Bureau International Des Poids et Measures Severs, Pairs, 2010
(  0) 0) |
| [13] |
Agnew D C. SPOTL: Some Programs for Ocean-Tide Loading[R]. Scripps Institution of Oceanography, San Diego, 2012
(  0) 0) |
| [14] |
Scherneck H. Ocean Tide Loading Provider[EB/OL]. http://holt.oso.chalmers.se/loading/, 2017
(  0) 0) |
| [15] |
Jiang W P, Li Z, Dam T V, et al. Comparative Analysis of Different Environmental Loading Methods and Their Impacts on the GPS Height Time Series[J]. Journal of Geodesy, 2013, 87(7): 687-703 DOI:10.1007/s00190-013-0642-3
(  0) 0) |
2. Faculty of Geosciences and Environmental Engineering, Southwest Jiaotong University, West High-Tech Zone, Chengdu 611756, China
 2018, Vol. 38
2018, Vol. 38

