获取高精度的水汽含量(precipitable water vapor, PWV)能够更加准确地分析水汽的形成和演变,为预报灾害性天气提供理论指导[1]。很多学者对不同区域进行了相关研究。王皓[2]根据江苏地区的GPS资料分析了江苏地区的一次强对流降水的形成过程。向华等[3]利用地面大气水汽压资料,根据地面水汽压关系经验公式,分析湖北省年、季平均可降水量的时空分布特征。刘爱梅等[4]利用济南地区的GPS数据分析了GPS探测和探空探测所得的可降水量的相关性。欧阳明达等[5]利用陆态网络基准站观测数据,采用GAMIT软件解算华中某地的可降水量,分析反演结果的精度与可行性。此外,利用GPS遥感资料和NCEP资料进行大气可降水量的研究也取得了较好的成果。
四川地区由于其复杂的地形和特殊的气候成为许多学者的研究对象。李国平[6]采用GPS遥感技术对四川盆地的水汽含量进行首次实验,揭示不同气候背景下GPS遥感大气水汽的异同,并分析可降水量的时间与空间分布特征。青盛等[7]利用Bernese软件反演成都地区2005-07~09的可降水量,证实GPS水汽反演在成都地区的可行性。近年来,四川CORS站的扩建与升级为四川地区空中水资源的整体分布和变化分析研究提供了更加完整的数据来源[8]。
1 数据选取与解算策略选取四川省不同地形地势下58个连续运行参考站,为提高解算精度,加入BJFS、CHAN、KUNM、LHZA、SHAO、URUM、GUAO和WUHN等8个国内永久性IGS跟踪站[9]。资料的时段为2012-01~2014-12,采样频率为30 s,数据解算结果为1 h解,每个站的有效数据量约为26 280个。
采用GAMIT软件进行数据处理,该软件采用双差观测量的方法,可以较好地消除卫星钟差和接收机钟差的影响,得到精度较高的解算结果[10]。GAMIT解算过程中,可根据用户设置参数的不同得到不同的解算结果。本文采用的解算策略为:1)轨道解类型采用松弛解;2)解算数据间隔为1 h;3)采用“全球气压和温度”模型值作为某一测站的先验气压和温度;4)结合map.grid和VMF1映射函数来反演水汽含量;5)采用CODE的电离层产品;6)考虑大气负荷和海潮负荷。
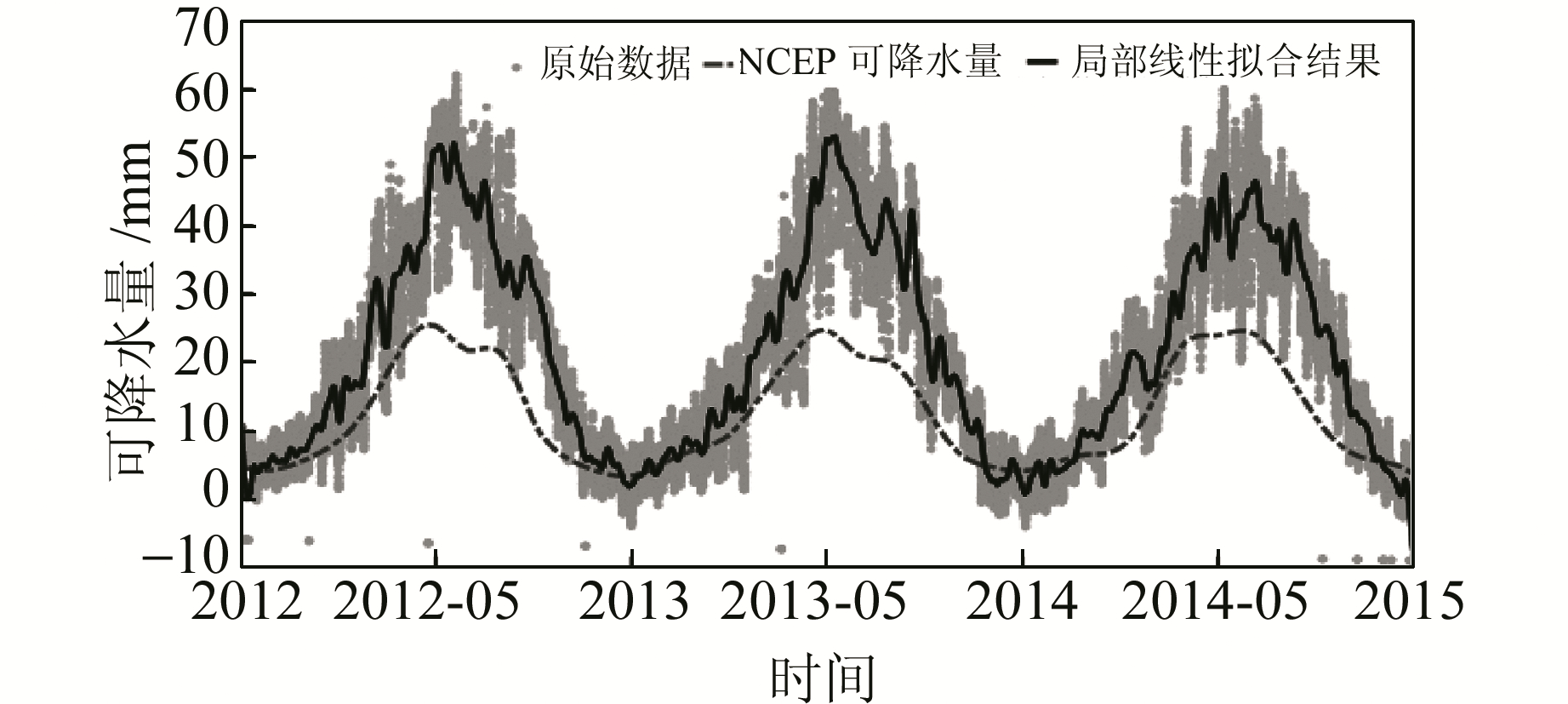
利用2012~2014年的NCEP水汽含量数据进行GPS与成都地区同时段NCEP水汽含量的对比。从图 1可以看出,两者水汽含量的波动周期与趋势一致。通过相关性分析,两种探测方法得到的水汽含量在时间变化上具有很好的相关性,相关系数为0.89,证明四川地区GPS探测水汽含量具有可用性。
|
图 1 GPS水汽反演结果与NCEP水汽含量数据的比较 Fig. 1 The comparison of PWV by GPS and NCEP |
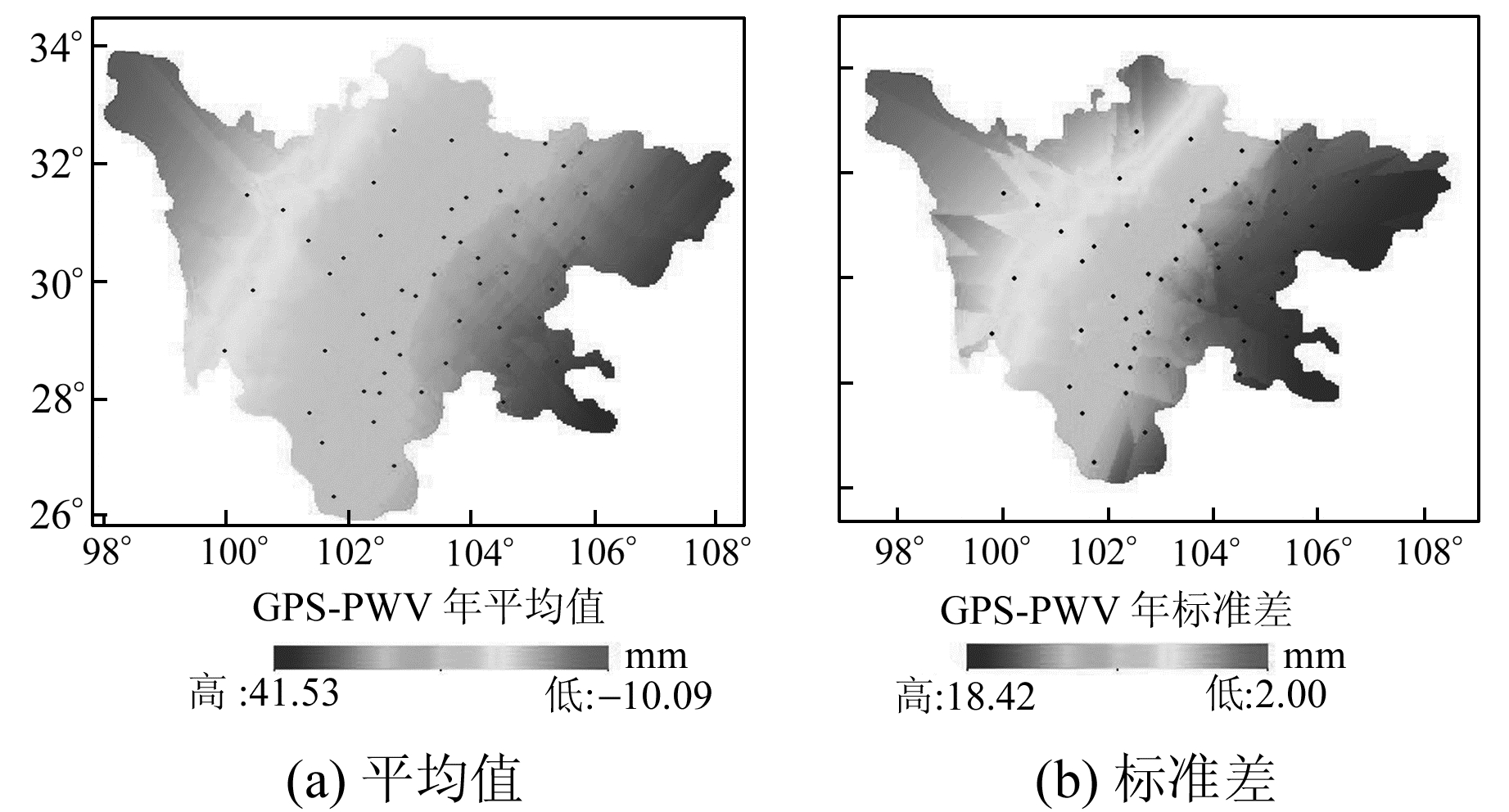
四川省位于我国西南腹地,地形复杂多变,包括盆地、平原、丘陵和高原,导致水汽含量的空间分布特征呈现很大差异。为了体现水汽含量在空间位置上的整体分布特征及变化趋势,采用Kriging插值法对四川省58个CORS站的数据资料进行插值处理[11]。
图 2(a)为四川地区年平均水汽含量的空间插值分布图,图 2(b)为四川地区年水汽含量标准差的空间插值分布图。对比发现,水汽含量呈现东多西少的特点,且按照东北-西南方向呈现条带状分布。
|
图 2 GPS-PWV年平均值及标准差的空间分布 Fig. 2 The spatial distribution of annual average and its standard deviation of GPS-PWV |
采用多元线性回归分析法和主成分分析法定量分析水汽含量与地形地势的关系。
2.1 多元线性回归分析多元线性回归分析主要研究因变量Y与多个自变量X1,X2,…,Xk之间的线性关系,其数学模型为:
| $ {Y_i} = {\beta _0} + {\beta _1}{X_{1i}} + {\beta _2}{X_{2i}} + \cdots + {\beta _k}{X_{ki}} + {\varepsilon _i} $ | (1) |
保持其他变量系数不变,只考虑Y与其中某变量Xi(i=1,2,…,k)的关系时,式(1)被称为偏相关。通过检验P值的大小反映回归方程是否有意义,即证明自变量和因变量间是否存在式(1)所描述的线性关系。如果P值小于0.05(α=0.05),则认为所建立的方程是有意义的,反之则无意义[12]。
分析得出,所建立的回归模型具有统计学意义(P=0.000),可认为模型较好地反映了经纬度及高程对水汽含量的共同影响。表 1说明,单独的因变量对水汽含量的变化无影响,这说明解释变量之间存在多重共线性问题,需要进一步讨论。
|
|
表 1 回归分析结果 Tab. 1 The results of regression analysis |
采用主成分分析法(principal component analysis,PCA)选出多个主成分来代表原来众多的变量,以消除多重共线性对拟合结果的影响。这些主成分应尽可能地反映所有变量的信息,各主成分之间互不相关[13]。
所有主成分可表示为:
| $ {z_1} = 0.522{\rm{std}}B + 0.175{\rm{std}}L-0.482{\rm{std}}H $ | (2) |
| $ {Z_2} = 0.039{\rm{std}}B + 0.909{\rm{std}}L + 0.373{\rm{std}}H $ | (3) |
式中,z1为第一主成分,z2为第二主成分。
再利用主成分进行回归分析,结果显示,各主成分都具有统计学意义(表 2)。
|
|
表 2 用两个主成分进行回归分析的结果 Tab. 2 Regression results of two PCs |
由此可得到因变量PWV与原自变量经度、纬度、高程的线性回归方程为:
| $ {\rm{PWV = 62}}{\rm{.832}}-{\rm{0}}{\rm{.208}}B-0.284L-0.007H $ |
式中,B为经度,L为高程,H为纬度。
为了进一步检验回归方程的精度,本文采用未参与回归建模的基站对该模型进行精度评估,评估结果如表 3所示。结果表明,利用未参与建模基站的水汽含量评估回归方程,其BIAS最大不超过3 mm,平均为0.242 mm,满足回归要求。
|
|
表 3 回归分析结果精度评定 Tab. 3 The accuracy of regression results |
由上述公式可以看出,水汽含量与该地区的地理经度、纬度和海拔高度存在线性关系。再结合四川省西高东低的地形特征,正好与梁宏等[14]提出的“地理纬度和海拔高度决定了高原及其周边地区南湿北干的大气水汽分布的特征”相吻合。
3 GPS-PWV时间序列分析四川省水汽含量不仅受经纬度、地形因子的影响,同时也受季节因素的影响。为了更深入地探究四川地区水汽含量存在的周期特性,利用改进的经验模态分解(modified ensemble empirical mode decomposition,MEEMD)[15]算法分析四川省CORS站2012~2014年的水汽时间序列,并结合频谱分析法研究它们的周期特征。MEEMD是利用排列熵来研究分解信号的随机性,避免了不必要的集成平均,使分解结果中出现虚假信号的几率更小。这里以不同海拔高度的CHDU、YBIN和HONY 3个站为例进行分析(图 3)。

|
图 3 四川省CHDU、YBIN和HONY 3个站3 a原始序列与局部线性拟合结果及MEEMD分解结果 Fig. 3 Primitive sequence and the results of local linear fitting of CHDU、YBIN and HONY stations of Sichuan province in 3 years and the results of MEEMD decomposition (a)~(c)为CHDU、YBIN和HONY 3个站3 a原始序列与局部线性拟合结果;(d)~(f)为对应的MEEMD分解结果 |
图 3(a)~(c)是长时间原始序列图,利用局部线性拟合去除原始数据中存在的异常值,拟合长度设置为半个月,使水汽含量的半月和月变化特性得以保留。图 3(d)~(f)为利用MEEMD分解的结果,倒数第2行为周年震荡,倒数第6行为半周年震荡,该曲线显示每年的4月和8月水汽含量都会出现异常增多的现象。可以发现,CHDU站和YBIN站年周期振幅均为25 mm,HONY站年周期振幅为16 mm,且波形规整,周年特性明显。
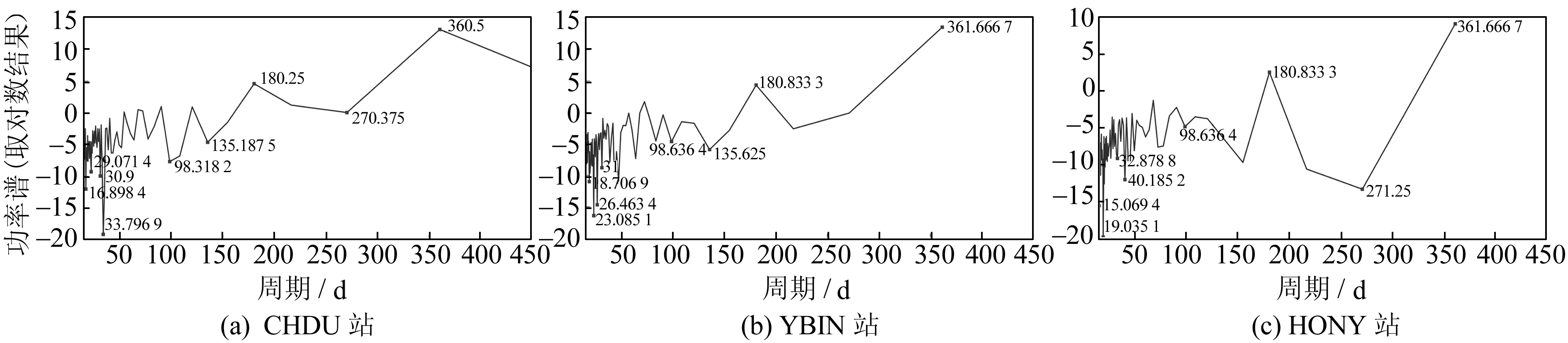
为进一步分析大气水汽含量中存在的循环周期,对3个站2012~2014年的PWV数据进行频谱分析。如图 4所示,3个站的大气水汽含量均存在约16 d、21 d、31 d、98 d、180 d、361 d的循环周期。
|
图 4 利用快速傅里叶变换得到的CHDU、YBIN、HONY站PWV循环周期图 Fig. 4 The cycle diagrams of the PWV of CHDU、YBIN and HONY stations by using the fast Fourier transform |
本文利用四川地区58个CORS站2012~2014年的数据,使用GAMIT软件反演出该地区大气水汽含量,分析水汽含量的时空分布特征和变化趋势,得到如下结论。
1) 利用多元线性回归分析法和PCA法建立四川地区水汽含量与其影响因素经度、纬度和高程之间的回归方程为PWV=62.832-0.208B-0.284L-0.007H。利用未参与建模的7个CORS站的数据对回归方程的精度进行检验,结果表明,BIAS最大不超过3 mm,平均为0.242 mm,回归效果良好。
2) 利用改进的经验模态分解结合频谱分析的方法,对四川省CHDU、YBIN和HONY测站水汽含量的周期变化进行分析,得到周年变化和趋势项。结果表明,3个站的水汽含量存在相同的约为16 d、21 d、31 d、98 d、180 d、361 d的循环周期。
致谢 感谢四川省地震局和中国陆态网提供数据。
| [1] |
徐祥德, 陶诗言, 王继志, 等. 青藏高原-季风水汽输送"大三角扇形"影响域特征与中国区域旱涝异常的关系[J]. 气象学报, 2002, 60(3): 258-266 (Xu Xiangde, Tao Shiyan, Wang Jizhi, et al. The Relationship between Water Vapor Transportation Features of Tibetan Plateau-Monsoon "Large Triangle Affecting Region"and Abnormal Drought-Flood of China[J]. Acta Meteorologica Sinica, 2002, 60(3): 258-266)
(  0) 0) |
| [2] |
王皓. 地基GPS的资料处理及在天气分析中的应用[D]. 南京: 南京信息工程大学, 2013 (Wang Hao. Ground-Based GPS Data Processing and Application in Weather Analysis[D]. Nanjing: Nanjing University of Information Science & Technology, 2013)
(  0) 0) |
| [3] |
向华, 周月华, 王海军. 湖北省空中水资源分析[J]. 暴雨灾害, 2007, 26(2): 134-138 (Xiang Hua, Zhou Yuehua, Wang Haijun. A Climatic Research of Cloud-Water Resources in Hubei Province[J]. Torrential Rain and Disasters, 2007, 26(2): 134-138)
(  0) 0) |
| [4] |
刘爱梅, 胡鹏, 尹承美, 等. GPS水汽反演资料在济南地区的应用[J]. 气象科学, 2010, 30(4): 555-558 (Liu Aimei, Hu Peng, Yin Chengmei, et al. The Application of GPS-PWV Computing Data in Jinan Area[J]. Journal of the Meteorological Sciences, 2010, 30(4): 555-558)
(  0) 0) |
| [5] |
欧阳明达, 张海东, 张英利. 基于陆态网络的区域水汽变化分析[J]. 全球定位系统, 2014, 39(1): 61-75 (Ouyang Mingda, Zhang Haidong, Zhang Yingli. Analysis of Reglonal Water Vapor Changing Based on CMONOC[J]. GNSS World of China, 2014, 39(1): 61-75)
(  0) 0) |
| [6] |
李国平. 地基GPS遥感大气可降水量及其在气象中的应用研究[D]. 成都: 西南交通大学, 2007 (Li Guoping. On the Remote Sensing of Precipitable Water Vapor Using Ground-Based GPS Technique and Applications in Meteorology[D]. Chengdu: Southwest Jiaotong University, 2007) http://cdmd.cnki.com.cn/Article/CDMD-10613-2008042015.htm
(  0) 0) |
| [7] |
青盛, 吕弋培, 黄丁发, 等. GPS水汽反演在成都地区的应用[J]. 四川测绘, 2008, 31(3): 121-123 (Qing Sheng, Lü Yipei, Huang Dingfa, et al. The Application of GPS-PWV Computing in Chengdu Area[J]. Surveying and Mapping of Sichuan, 2008, 31(3): 121-123)
(  0) 0) |
| [8] |
林丹, 王维佳, 李慧晶. 西南地区可降水量时空分布和变化特征[J]. 气象科技, 2013, 41(5): 889-894 (Lin Dan, Wang Weijia, Li Huijing. Distribution and Variation of Precipitable Water in Southwest China[J]. Metrorolgical Science and Technology, 2013, 41(5): 889-894)
(  0) 0) |
| [9] |
赵倩, 沈飞. 江苏省CORS系统解算中IGS基准站选取的研究[J]. 测绘科学, 2011, 36(6): 124-126 (Zhao Qian, Shen Fei. Selection of IGS Reference Stations in Data Processing of Jiangsu CORS[J]. Science of Surveying and Mapping, 2011, 36(6): 124-126)
(  0) 0) |
| [10] |
赵建三, 杨创, 闻德保. 利用GAMIT进行高精度GPS基线解算的方法及精度分析[J]. 测绘通报, 2011(8): 5-9 (Zhao Jiansan, Yang Chuang, Wen Debao. Method and Precision Analysis of High-Precision GPS Baseline Solution by GAMIT[J]. Bulletin of Surveying and Mapping, 2011(8): 5-9)
(  0) 0) |
| [11] |
孔令娜, 向南平. 基于ArcGIS的降水量空间插值方法研究[J]. 测绘与空间地理信息, 2012, 35(3): 123-126 (Kong Lingna, Xiang Nanping. Research on Rainfall Spatial Interpolation Methods Based on ArcGIS[J]. Geomatics & Spatial Information Technology, 2012, 35(3): 123-126)
(  0) 0) |
| [12] |
王文博. 计量经济学[M]. 西安: 西安交通大学出版社, 2004 (Wang Wenbo. Econometrics[M]. Xi'an: Xi'an Jiaotong University Press, 2004)
(  0) 0) |
| [13] |
赵焕宸. 东北地区降水分布特性的主成分分析[J]. 地理科学, 1984, 4(8): 225-234 (Zhao Huanchen. An Analysis of Principal Components for Distributive Characteristics of Precipitation in Northeast China[J]. Scientia Geographica Sinica, 1984, 4(8): 225-234)
(  0) 0) |
| [14] |
梁宏, 刘晶淼, 李世奎. 青藏高原及周边地区大气水汽资源分布和季节变化特征分析[J]. 自然资源学报, 2006, 21(4): 526-534 (Liang Hong, Liu Jingmiao, Li Shikui. Analysis of Precipitable Water Vapor Source Distribution and Its Seasonal Variation Characteristics over Tibetan Plateau and Its Surroundings[J]. Journal of Natural Resources, 2006, 21(4): 526-534 DOI:10.11849/zrzyxb.2006.04.004)
(  0) 0) |
| [15] |
郑近德, 程军圣, 杨宇. 改进的EEMD算法及其应用研究[J]. 振动与冲击, 2013, 32(21): 21-46 (Zhang Jinde, Cheng Junsheng, Yang Yu. Modified EEMD Algorithm and Its Applications[J]. Journal of Vibration and Shock, 2013, 32(21): 21-46 DOI:10.3969/j.issn.1000-3835.2013.21.004)
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38

