2. 广西空间信息与测绘重点实验室,桂林市雁山街319号,541006
电离层总电子含量(TEC)能直接影响卫星的定位精度[1-3],其异常变化通常是地震等地质灾害的前兆[4-6],因此对电离层TEC值的预报具有重要的意义。目前预测电离层TEC主要有两种模型,一是经验电离层模型,如Klobuchar模型和IRI模型,但单频接收机常使用的Klobuchar模型的精度仅为50%~60%,且固定夜间初始相位具有明显的不合理性[7];IRI模型所需参数较多,且具有地域局限性[8]。二是线性与非线性预报模型,如时间序列[9-10]和神经网络[11]等,时间序列在以往的研究中被广泛使用,但往往没有很好地说明样本序列长度的选取标准,也没有全面地考虑纬度因素对预报精度的影响,且实验数据量少,结论不具有一般性。
本文通过对不同长度的样本序列进行5 d短期预报并分析预报精度,选取合适的样本序列长度,采用IGS中心发布的电离层TEC格网数据,分别使用季节性时间序列模型SARIMA及Holt-Winters加法、乘法模型,对北半球不同纬度48个区域的TEC值进行预报,并与IGS观测值进行对比,分析预报值的误差随纬度的变化规律。
1 季节性时序模型 1.1 SARIMA模型简介ARMA(p, q)模型将d阶差分后的平稳序列进行拟合,再通过d阶差分还原得到预报值。ARMA(p, q)模型的表达式如下:
| $ \begin{array}{l} {x_t} = {\varphi _1}{x_{t-1}} + {\varphi _2}{x_{t-2}} + ... + {\varphi _p}{x_{t-p}} + \\ {\varepsilon _t} + {\theta _1}{\varepsilon _{t - 1}} + {\theta _2}{\varepsilon _{t - 2}} + ... + {\theta _q}{\varepsilon _{t - q}} \end{array} $ | (1) |
式中,φ1, φ2, …, φp为自回归参数,θ1, θ2, …, θq为移动平均参数,εt为白噪声序列。
但传统的ARMA模型在处理季节性问题时具有参数过多和模型结构复杂等缺点。季节性差分自回归移动平均模型(seasonal autoregressive integrated moving average,SARIMA)是自回归移动平均模型(ARMA)的扩展。通过将非平稳的时间序列进行d阶差分和D阶季节差分,得到平稳的序列,建立SARIMA(p, d, q)×(P, D, Q)S模型:
| $ \varphi (B)\mathit{\Phi} ({B^S}){\nabla ^d}\nabla _S^D{y_t} = \theta (B)\Theta ({B^S}){\varepsilon _t} $ | (2) |
式中,D阶季节差分∇SD=(1-BS)D,Φ(BS)为季节自回归算子,Θ(BS)为季节移动平均算子,S为季节周期。
1.2 Holt-Winters指数平滑法Holt-Winters是一种指数平滑法,该模型有3种形式:无季节模型、加法模型和乘法模型。其中加法模型和乘法模型可以对样本序列的长期趋势、趋势增量以及季节变动作出估计[12],对季节性趋势较强的数据具有较好的预报能力[13]。
Holt-Winters加法模型:
| $ \left\{ \begin{array}{l} {S_{\rm{t}}} = \alpha ({X_t}-{I_{t-L}}) + (1-\alpha )({S_{t - 1}} - {b_{t - 1}})\\ {I_t} = \beta ({X_t} - {S_t}) + (1 - \beta ){I_{t - L}}\\ {b_t} = \gamma ({S_t} - {S_{t - 1}}) + (1 - \gamma ){b_{t - 1}}\\ {F_{t + m}} = {S_t} + m{b_t} + {I_{t - L + m}} \end{array} \right. $ | (3) |
Holt-Winters乘法模型:
| $ \left\{ \begin{array}{l} {S_{\rm{t}}} = \alpha (\frac{{{X_t}}}{{{I_{t-L}}}}) + (1-\alpha )({S_{t-1}} - {b_{t - 1}})\\ {I_t} = \beta (\frac{{{X_t}}}{{{S_t}}}) + (1 - \beta ){I_{t - L}}\\ {b_t} = \gamma ({S_t} - {S_{t - 1}}) + (1 - \gamma ){b_{t - 1}}\\ {F_{t + m}} = ({S_t} + m{b_t}){I_{t - L + m}} \end{array} \right. $ | (4) |
式中,Xt为观测值,St为稳定成分,其初始值为
短期预报中,样本序列的长度对预报精度有较大的影响。随着样本序列长度的增加,预报精度会提高,但当序列增加到一定的长度后,预报精度会趋于稳定,甚至会随序列长度的增加而降低。为使预报效果达到最佳,对实验数据进行测试,用不同长度的样本序列进行5 d预报,直至预报精度达到最高(精度评定标准为下文式(5)、(6))。此外,太阳的剧烈活动与地磁场的变化都会造成电离层的异常扰动。太阳活动呈现出11 a的周期性[14],因此,本文根据地磁指数的变化情况,选取太阳活动较为平静的2009年年积日175~194(06-24~07-13)的电离层TEC格网数据进行实验,同时给出此期间内表示地磁活动强度的Kp指数和表示环电流强度的Dst指数。
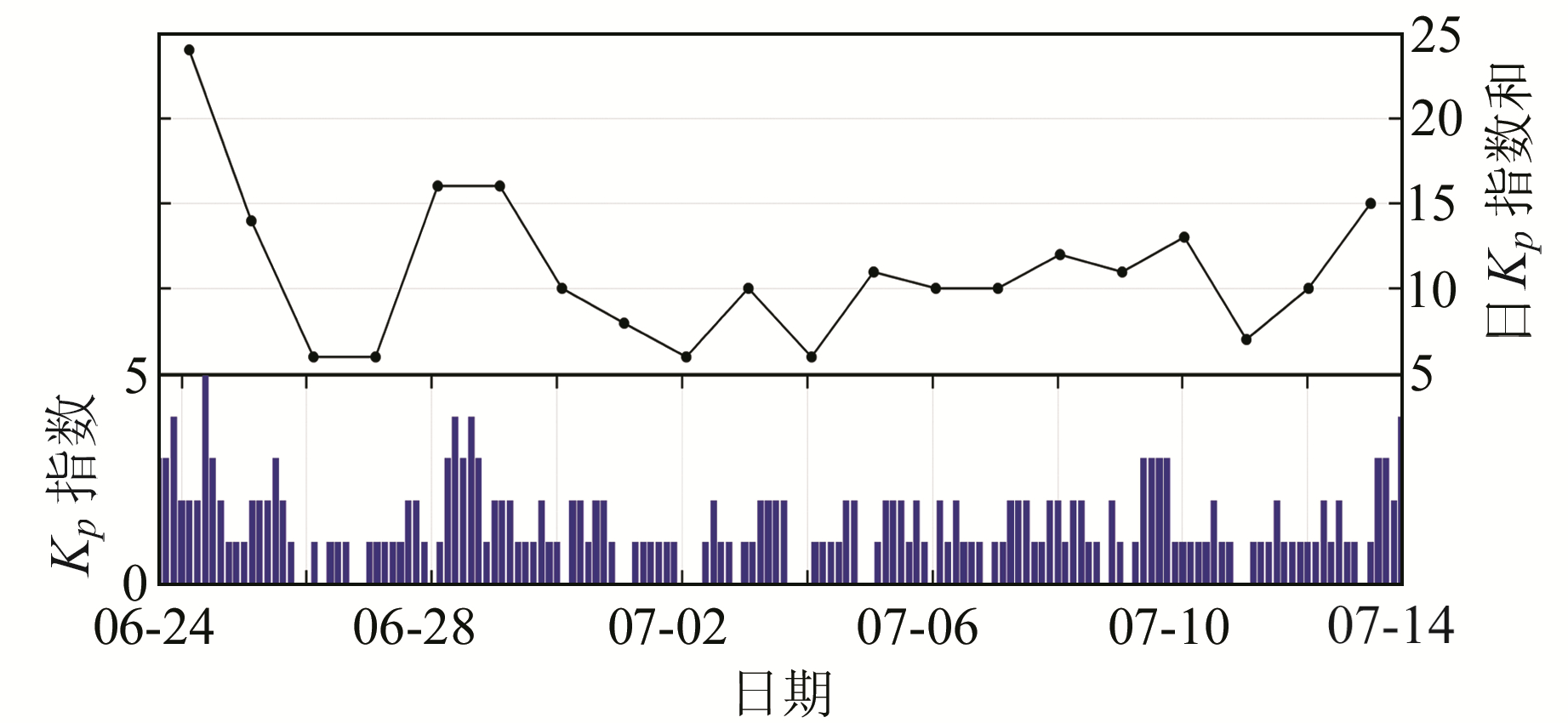
Kp指数用来描述地磁活动的强度,每天共8个值,一般认为日Kp指数之和大于30则地磁活动强烈。从图 1可以看出,预报期内各个时段的Kp值均小于5且每天的Kp指数之和小于25,地磁活动平稳。Dst指数用于表征全球的环电流强度,时间分辨率为1 h,一般当Dst指数低于-30 nT时可能发生小磁暴,处于-30 ~-50 nT时可能发生中等磁暴,处于-100 nT以下时可能发生大磁暴。图 2给出预测期的Dst指数均不低于-30 nT,不可能发生磁暴。综上所述,地磁活动与磁暴对模型预报的影响可以忽略。
|
图 1 预报期Kp指数 Fig. 1 Kp index in forecast period |

|
图 2 预报期Dst指数 Fig. 2 Dst index in forecast period |
利用SARIMA和Holt-Winters指数平滑模型,采用IGS中心提供的2009年年积日175~189的电离层TEC格网数据作为样本序列,对北半球6条经线上48个不同纬度格网点的TEC值进行5 d预报。由于篇幅有限,在此仅具体分析120°E,5°~75°N(间隔10°)共8个区域的预报结果。将模型的预报结果与IGS的观测值进行比较,通过定义日均相对精度P和均方根误差RMSE来评定模型的预报精度,其表达式为:
| $ P = \frac{1}{n}\sum\limits_{t = 1}^n {(1-\frac{{|{I_{{\rm{pre}}}}-{I_{{\rm{IGS}}}}|}}{{{I_{{\rm{IGS}}}}}} \times 100\% )} $ | (5) |
| $ {\rm{RMSE}} = \sqrt {\frac{1}{n}{{\sum\limits_{t = 1}^n {({I_{{\rm{pre}}}}-{I_{{\rm{IGS}}}})} }^2}} $ | (6) |
式中,Ipre为模型的预报值,IIGS为IGS中心提供的观测值,t为历元,n为一天观测的历元数。
3种模型8个纬度地区TEC值的预报结果与残差分布如图 3所示。从IGS给出的观测值可以看出,TEC的变化幅度随纬度的降低而增大,且低纬度区域的TEC变化周期性更为明显。在任何纬度,3种模型均能较好地反映电离层TEC的变化,且SARIMA模型的预报效果略高于Holt-Winters模型。通过预报值残差可以看出,TEC预报值与观测值的误差在25°N及以下的低纬地区要大于35°N以上的中、高纬地区。

|
图 3 不同纬度地区TEC 5 d预报结果及残差 Fig. 3 5 d forecast results and residual of TEC in different latitudes |
表 1给出了不同纬度上3种模型预报值的残差统计结果。综合3种模型的残差百分比统计可以看出,65°N以上的高纬地区的残差值最小,有85%的残差值小于1 TECu,没有大于3 TECu的残差值;25°N及以下地区的残差值最大,其中5°N地区仅55.44%的残差小于1 TECu,17.78%的残差大于3 TECu;35°N和45°N地区的残差也较小,其中35°N地区有72.22%的残差小于1 TECu,没有残差大于3 TECu。
|
|
表 1 预报值残差(Δ)百分比统计 Tab. 1 Forecast residual (Δ) percentage statistics |
将120°E经线上8个纬度区域的5 d预报值与IGS的观测值进行对比,计算得到其日均相对精度P,如表 2所示。可以看出,SARIMA模型预报值的5 d日均相对精度平均值为82.70%~92.99%,Holt-Winters模型的日均相对精度平均值为80.21%~93.73%。从相对精度随预报时间的变化来看,3种模型都能较好地反映电离层TEC值的变化规律。从纬度变化来看,低纬25°地区和中高纬55°地区预报值的相对精度要低于其他纬度。综合3种模型的5 d日均相对精度平均值可以看出,高纬65°及以上地区和中纬35°地区的预报精度最高。
|
|
表 2 日均相对精度(P)统计 Tab. 2 Daily average relative accuracy (P) statistical analysis |
表 3给出了3种模型在120°E经线上8个纬度区域每天预报值的均方根误差。可以看出,其随时间的变化相对较为稳定,因此使用季节性时间序列模型进行短期预报具有一定的可靠性。SARIMA和加法模型在各个纬度都具有较高的预报精度,其均方根误差均小于2 TECu;乘法模型在中纬和高纬的预报效果较好,在低纬的预报精度最低,均方根误差最大为3.09 TECu。总体而言,3种模型均方根误差的峰值出现在北纬25°和55°地区,谷值出现在高纬65°及以上地区和中纬度的35°附近。
|
|
表 3 均方根误差(RMSE)统计 Tab. 3 Root mean square error (RMSE) statistical analysis |
|
|
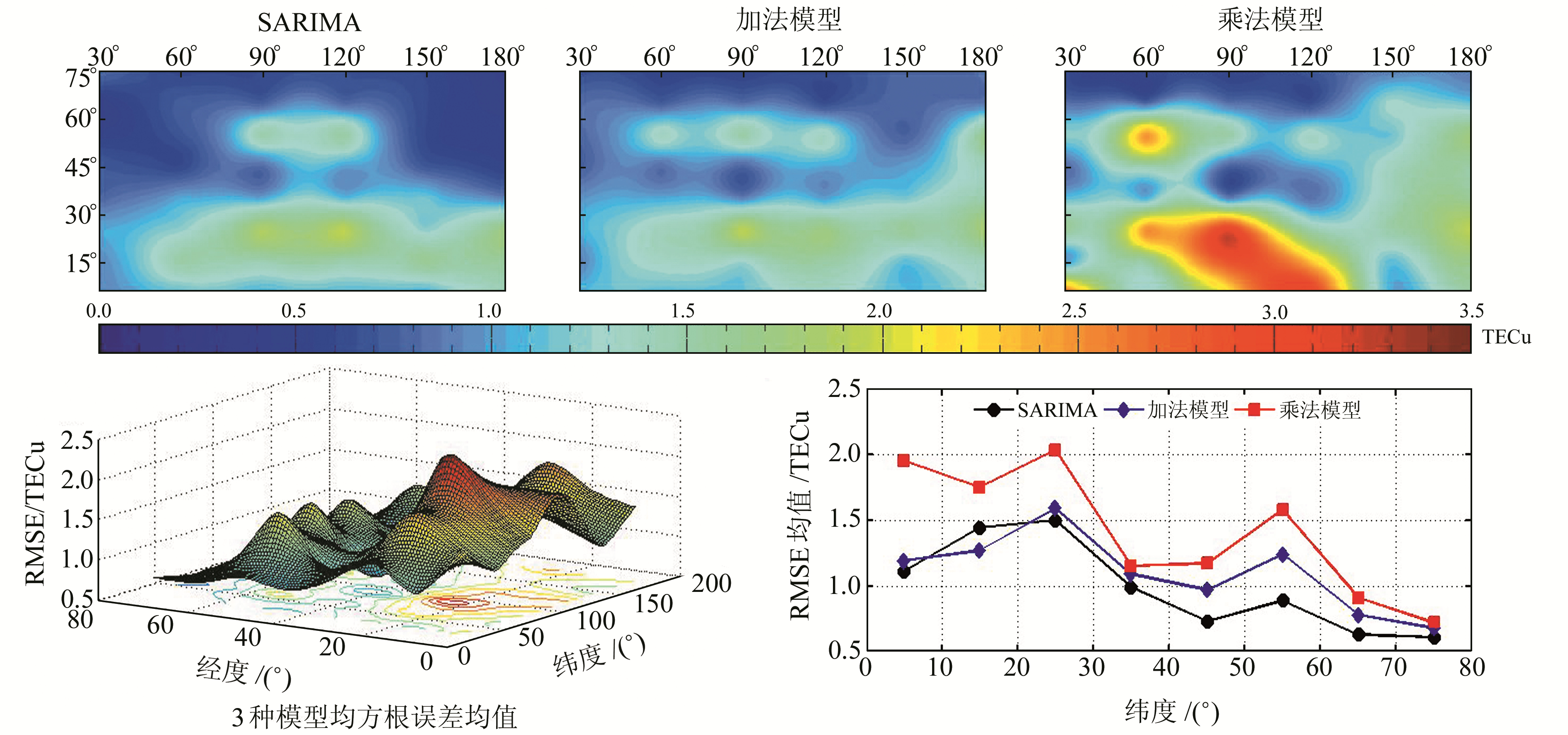
表 4 北半球48个区域RMSE统计 Tab. 4 RMSE statistics of 48 regions in Northern Hemisphere |
|
图 4 均方根误差随纬度的变化规律 Fig. 4 Variation of root mean square error with latitude |
本文综合考虑了样本序列长度对短期预报的影响和太阳与地磁活动对电离层的影响,选取平静期北半球的48个纬度地区进行详细分析,使用季节性时间序列模型进行预报并评估预报精度,得到以下结论:
1) 从时间上看,3种模型均能较好地反映电离层TEC值的变化趋势,SARIMA模型的预报精度最高,其次为加法模型,乘法模型最低。
2) 通过分析TEC预报结果的日均相对精度和均方根误差发现,北纬25°和55°地区预报精度最低,均方根误差表现为一大一小两个峰值,而在北纬35°~45°区域和65°以上地区的预报精度较高,并且均方根误差随纬度的降低总体呈现出增长趋势。
本次研究对不同纬度地区电离层TEC预报模型以及样本序列长度的选取具有一定的指导意义,其均方根误差随纬度的变化在实际应用中具有一定的参考价值。但IGS提供的电离层格网数据本身带有误差,且由于数据的局限性,没有很好地分析局部地区电离层的异常扰动造成局部预报精度下降的可能性。
| [1] |
章红平. 基于地基GPS的中国区域电离层监测与延迟改正研究[D]. 上海: 中国科学院上海天文台, 2006 (Zhang Hongping. Study on Regional Ionospheric Monitoring and Delay Correction in China Based on GPS[D]. Shanghai: Shanghai Astronomical Observatory, CAS, 2006) http://cdmd.cnki.com.cn/Article/CDMD-80022-2006109504.htm
(  0) 0) |
| [2] |
邓忠新. 电离层TEC暴及其预报方法研究[D]. 武汉: 武汉大学, 2012 (Deng Zhongxin. Study on the Ionospheric TEC Storm and Its Forecasting Method[D]. Wuhan: Wuhan University, 2012)
(  0) 0) |
| [3] |
张勇, 张斌, 马能武. 单频GPS接收机的电离层延迟改正模型研究[J]. 大地测量与地球动力学, 2012, 32(2): 69-73 (Zhang Yong, Zhang Bin, Ma Nengwu. On Models of Ionospheric Delay Correction for Single-Frequency GPS Receiver[J]. Journal of Geodesy and Geodynamics, 2012, 32(2): 69-73)
(  0) 0) |
| [4] |
李磊, 张淑芳, 胡青, 等. ARMA模型在地震电离层TEC异常探测中的应用[J]. 大地测量与地球动力学, 2015, 35(1): 62-66 (Li Lei, Zhang Shufang, Hu Qing, et al. Application of ARMA Model in Detecting Ionospheric TEC Anomaly Prior to Earthquake[J]. Journal of Geodesy and Geodynamics, 2015, 35(1): 62-66)
(  0) 0) |
| [5] |
王若鹏. 地震电离层前兆短期预报研究[D]. 武汉: 武汉大学, 2012 (Wang Ruopeng. Study on Short-Term Forecasting of the Ionospheric Precursors of Earthquake[D]. Wuhan: Wuhan University, 2012)
(  0) 0) |
| [6] |
孟泱, 王泽民, 鄂栋臣. 基于GPS数据的地震前电离层TEC异常研究[J]. 武汉大学学报:信息科学版, 2008, 33(1): 81-84 (Meng Yang, Wang Zemin, E Dongchen. Ionopsheric TEC Anomalies of Pre-Earthquake Based on GPS Data[J]. Geomatics and Information Science of Wuhan University, 2008, 33(1): 81-84)
(  0) 0) |
| [7] |
蔡成辉, 刘立龙, 黎峻宇, 等. 基于改进的Klobuchar模型建立南宁市区域电离层延迟模型[J]. 大地测量与地球动力学, 2015, 35(5): 797-806 (Cai Chenghui, Liu Lilong, Li Junyu, et al. Establishment of Region Ionospheric Delay Model in Nanning Based on Improved Klobuchar Model[J]. Journal of Geodesy and Geodynamics, 2015, 35(5): 797-806)
(  0) 0) |
| [8] |
章红平, 平劲松, 朱文耀, 等. 电离层延迟改正模型综述[J]. 天文学进展, 2006, 24(1): 16-26 (Zhang Hongping, Ping Jingsong, Zhu Wenyao, et al. Brief Review of the Ionospheric Delay Models[J]. Progress in Astronomy, 2006, 24(1): 16-26)
(  0) 0) |
| [9] |
陈鹏, 姚宜斌, 吴寒. 利用时间序列分析预报电离层TEC[J]. 武汉大学学报:信息科学版, 2011, 36(3): 267-270 (Chen Peng, Yao Yibin, Wu Han. TEC Prediction of Ionosphere Based on Time Series Analysis[J]. Geomatics and Information Science of Wuhan University, 2011, 36(3): 267-270)
(  0) 0) |
| [10] |
张小红, 任晓东, 吴风波, 等. 自回归移动平均模型的电离层总电子含量短期预报[J]. 测绘学报, 2014, 43(2): 118-124 (Zhang Xiaohong, Ren Xiaodong, Wu Fengbo, et al. Short-Term TEC Prediction of Ionosphere Based on ARIMA Model[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(2): 118-124)
(  0) 0) |
| [11] |
王松寒. 区域电离层延迟改正及预报模型研究[D]. 南京: 东南大学, 2016 (Wang Songhan. Research on the Delay Correction Model and Forecasting Model of Regional Ionosphere[D]. Nanjing: Southeast University, 2016)
(  0) 0) |
| [12] |
席广永, 越建平, 周宝兴. 基于Holt-Winter的电离层延迟预报模型[J]. 测绘通报, 2012(9): 7-10 (Xi Guangyong, Yue Jianping, Zhou Baoxing. The Forecasting Model of Ionospheric Delay Based on Holt-Winter[J]. Bulletin of Surveying and Mapping, 2012(9): 7-10)
(  0) 0) |
| [13] |
谢劭峰, 陈军, 黄良珂, 等. 基于Holt-Winters的电离层总电子含量预报[J]. 大地测量与地球动力学, 2017, 37(1): 72-76 (Xie Shaofeng, Chen Jun, Huang Liangke, et al. Ionospheric TEC Prediction Based on Holt-Winters Models[J]. Journal of Geodesy and Geodynamics, 2017, 37(1): 72-76)
(  0) 0) |
| [14] |
姚宜斌, 张顺, 孔建. 2011年电离层和太阳活动指数的准21.5天振荡分析[J]. 测绘学报, 2017, 46(1): 9-15 (Yao Yibin, Zhang Shun, Kong Jian. Analysis of ~21.5 d Period in Ionospheric and Solar Indices during 2011[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(1): 9-15 DOI:10.11947/j.AGCS.2017.20160067)
(  0) 0) |
2. Guangxi Key Laboratory of Spatial Information and Geomatics, 319 Yanshan Road, Guilin 541006, China
 2018, Vol. 38
2018, Vol. 38


