天顶对流层延迟(ZTD)模型大致可分为无实测气象参数的经验ZTD模型[1-5]和利用实测气象参数的气象参数ZTD模型[6-8]。前者方便用户使用,但精度难以满足精密工程测量需要;后者需要已知气象参数来计算对流层延迟,计算精度较高,主要有Hopfield模型、Saastamoinen模型、Black模型等。
对流层受到多种因素影响,存在很多不规则的变化。神经网络模型属于自适应非线性动力学系统,它具有学习、记忆、计算和智能处理功能,可从环境信息复杂、推理规则不明确的非线性空间系统中挖掘出隐含的规律。有学者利用神经网络建立模型进行对流层延迟变化的拟合[9-10]。模型误差一直是测绘领域待解决的难题之一,许多学者对此进行了研究,研究方法主要包括附加系统参数方法、最小二乘配置与推估、半参数模型等[11-13]。这些方法虽然取得了很大成效,但因受到人为假定函数关系的约束存在一定的局限性。对于形式简单的线性回归模型,这些方法的补偿效果较好,但是对于复杂的非线性模型,补偿效果有待提高。
为解决传统ZTD模型精度较低这一难题,本文把神经网络和模型误差进行组合,形成基于神经网络的模型误差补偿技术,并建立了一个适用于北半球的高精度ZTD融合模型。
1 对流层延迟近似“真值”的获取气象台站每天08:00和20:00各放飞一次高空探测气球来获得气象台站上空的气象资料。探测气球能获得一定等压面上的气象参数,包括温度、露点温度、风速风向和海拔高度。
本文利用Wyoming大学提供的北半球120多个测站2010年中具有代表性的6 d共753个气象探空数据进行研究。分析发现,在对流层及平流层范围内,各个气象参数所服从的函数模型与大气折射率随海拔高度呈现3段函数变化。因此,在求解对流层延迟时,将该层大气分为3段来考虑,具体积分过程如下:
| $ \delta =\\ \left\{ \begin{array}{l} {10^{- 6}}\int_{{h_0}}^{1000} {[N({h_0})-\Delta Nh]dh, {h_0} \le h < 1000m} \\ {10^{ - 6}}\int_{1000}^{11000} {[N(1000) \times \exp [-{c_1}(h-1000)]]{\rm{d}}h, 1000m \le h < 11000m} \\ {10^{ - 6}}\int_{11000}^{{h_T}} {[N(11000) \times \exp [-{c_2}(h-11000)]]{\rm{d}}h, 11000m \le h < {h_T}} \end{array} \right. $ | (1) |
式中,h0为测站处的海拔高度,hT为对流层顶,指大气折射率为0时的海拔高度,N(h)为海拔h处的大气折射率指数。
表 1为测站1028(74.50°N,19.00°E)在2010-01-01、03-01、05-01、07-01、09-01和11-01每天08:00的气象探空数据和由大气理论公式计算的对流层延迟近似“真值”(ZTD_TRU)。
|
|
表 1 测站1028的气象探空数据和ZTD_TRU Tab. 1 The meteorological sounding data of station 1028 and ZTD_TRU |
Hopfield模型将大气层分为对流层和电离层,通过分析对流层中各个气象参数与海拔高度之间的关系,推导出大气折射率指数和高程的关系,然后利用地面气象参数进行整个对流层延迟的计算。
折射率指数与大气压强、温度和水汽分压较为准确的一种计算公式为:
| $ \begin{array}{l} N(h) = 77.6 \times \frac{{{P_0}}}{{{T_0}}} \times {(\frac{{{H_T}-h}}{{{H_T}-{h_0}}})^4} + \\ 3.73 \times {10^5} \times \frac{{{e_0}}}{{{T_0}^2}}{(\frac{{{H_W}-h}}{{{H_W} - {h_0}}})^4} \end{array} $ | (2) |
式中,P0、h0、T0、e0分别为测站处的气压、高程、绝对温度和水汽分压,HW为湿对流层顶,一般情况下HW=11 000 m。
Hopfield模型就是沿海拔高度积分并舍去微小项,具体计算公式为:
| $ \begin{array}{l} \delta = {10^{- 6}} \times {k_1} \times \frac{{{P_0}}}{{{T_0}}} \times \frac{{{H_T}- h}}{5} + {10^{- 6}} \times \\ [{k_3} + 273({k_2}-{k_1})] \times \frac{{{e_0}}}{{{T_0}^2}} \times \frac{{{H_W} -h}}{5} \end{array} $ | (3) |
式中,k1、k2、k3为一组大气折射实验常数,通常由气象资料分析得到。本文分别取77.60 K/mbar、64.79 K/mbar、3.776×105 K2/mbar。
表 2为测站1028在2010-01-01、03-01、05-01、07-01、09-01和11-01每天08:00通过Hopfield模型计算的天顶方向对流层延迟(ZTD_HOP)。
|
|
表 2 测站1028的气象探空数据和ZTD_HOP Tab. 2 The meteorological sounding data of station 1028 and ZTD_TRU |
BP神经网络是一种按误差反向传播算法训练的多层前馈网络,它能学习和存储大量输入-输出模式的映射关系。BP神经网络不需要事先确定数学方程,而是通过反向传播误差不断调整网络的权值和阈值,使网络的误差平方和最小。BP神经网络模型不仅有输入层节点、输出层节点,而且有隐含层节点。对于输入信号,要先向前传播到隐含节点,经过激活函数后,再把隐含节点的输出信息传播到输出节点,最后给出输出结果。
BP神经网络模型的网络参数包括学习速率(η)、平滑因子(α)、学习误差(E)。η表示网络对学习样本进行训练学习时的速度,如果η取大值,则训练学习前期收敛速度快,但后期容易震荡;如果η取小值,则训练学习前期收敛速度慢,但后期容易稳定。α可实现全局学习速率自适应,加快收敛速度。E表示控制学习收敛的条件,一般E越小,检验中误差也越小,但如果E过小,会造成过拟合现象。
3 传统BP模型和融合模型的构建 3.1 传统BP模型BP神经网络中各层节点数的选择对网络的性能影响很大。传统BP模型的3个输入层节点分别为气压(P)、温度(T)和水汽压(e)。隐含层节点的选择是一个十分复杂的问题,对比分析后确定隐含层节点数为15。输出层节点为利用大气基本理论公式求得的天顶方向对流层延迟(ZTD_TRU)。采用控制变量法分析不同模型参数对训练模型精度的影响。经过大量实验,确定传统BP模型学习速率(η)取1.4,平滑因子(α)取0.6,学习误差(E)取0.09。传统BP模型的网络结构如图 1所示。
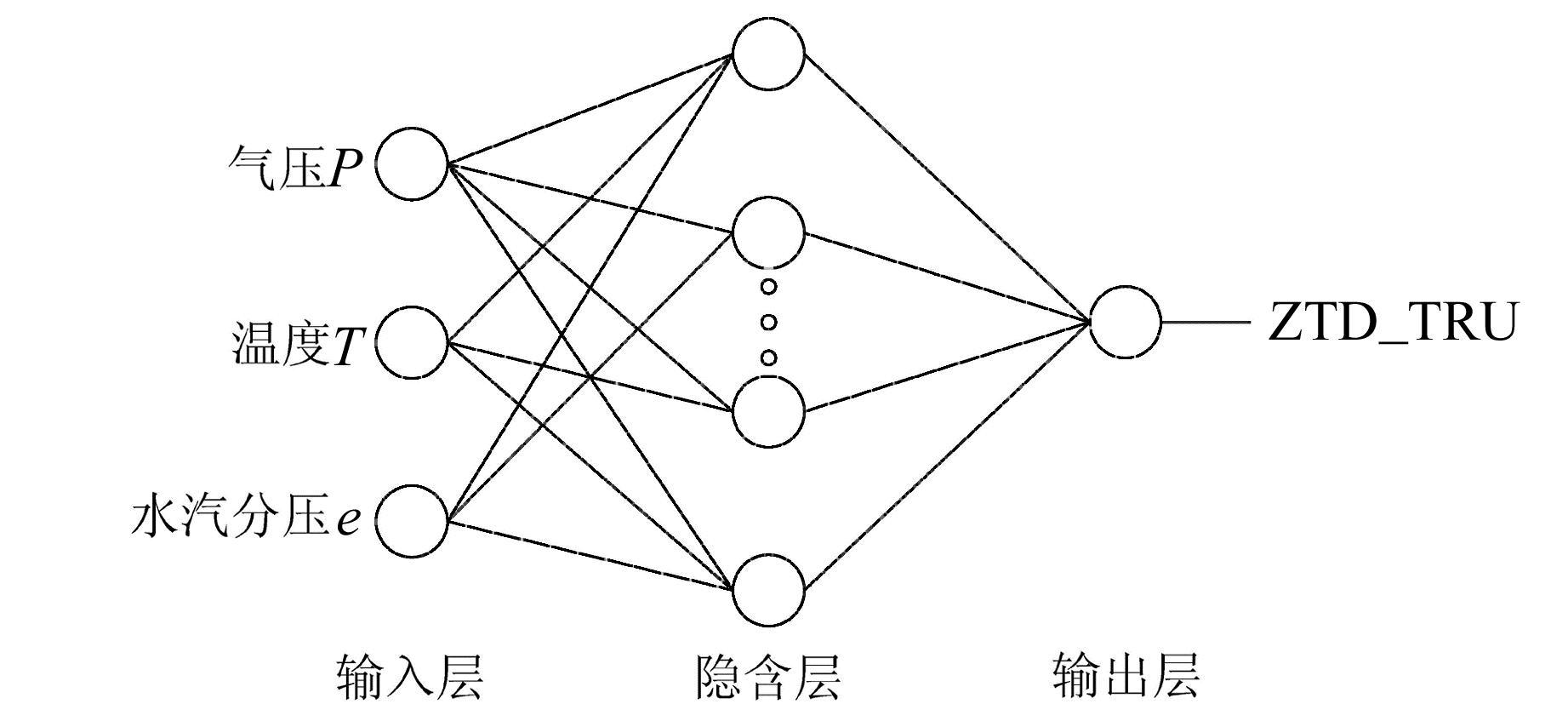
|
图 1 传统BP模型的网络结构 Fig. 1 The network structure of traditional BP model |
Hopfield模型计算对流层延迟时的模型误差为:
| $ {\rm{DHOP}} = {\rm{ZTD}}\_{\rm{TRU}}-{\rm{ZTD}}\_{\rm{HOP}} $ | (4) |
式中,ZTD_TRU为根据大气理论公式计算的对流层延迟近似“真值”,ZTD_HOP为由Hopfield模型计算的天顶对流层延迟。
选择单隐含层模式,经过大量实验最终确定隐含层节点数为25。输出层节点为DHOP,表示对流层延迟近似“真值”(ZTD_TRU)与Hopfield模型计算天顶对流层延迟(ZTD_HOP)之差。融合模型的网络结构如图 2所示。

|
图 2 融合模型的网络结构 Fig. 2 The network structure of fusion model |
选取Wyoming大学提供的北半球120多个测站2010年有代表性的6 d(共753个全球气象数据)验证融合模型的精度。从120多个测站中均匀选取50个作为学习测站进行神经网络的建模,剩下70多个测站作为检验测站来检验融合模型精度。
用平均偏差(BIAS)和均方根误差(RMSE)作为模型精度评价标准,计算公式为:
| $ {\rm{BIAS}} = \frac{1}{N}\sum\nolimits_{i = 1}^N {({\rm{ZTD}}_i^C-{\rm{ZTD}}\_{\rm{TRU}})} $ | (5) |
| $ {\rm{RMSE}} = \sqrt {\frac{1}{N}\sum\nolimits_{i = 1}^N {{{({\rm{ZTD}}_i^C-{\rm{ZTD}}\_{\rm{TRU}})}^2}} } $ | (6) |
式中,N为测试样本数量,ZTDiC为模型计算值,ZTD_TRU为真值。
对这6 d分别进行建模分析,Hopfield模型、传统BP模型和融合模型计算检验样本的精度指标具体结果如表 3所示,BIAS分布情况如图 3所示。
|
|
表 3 检验样本的精度指标 Tab. 3 The accuracy of the test sample |

|
图 3 3种模型的BIAS分布情况 Fig. 3 BIAS distribution of three models |
1) 相比传统BP模型和融合模型,Hopfield模型的绝对偏差最大,存在检验样本点整体的BIAS都大于0的现象,说明Hopfield模型在计算ZTD时存在一定的系统误差。
2) 融合模型的RMSE最小,为23.31 mm。传统BP模型在01-01和03-01的RMSE大于Hopfield模型,其余4 d模型精度都优于Hopfield模型。可能是因为这2 d传统BP模型的训练存在过拟合现象,导致预测误差偏大。Hopfield模型的RMSE最大,为35.31 mm。相比Hopfield模型精度,融合模型的精度提高约34%。
3) Hopfield模型的BIAS整体波动幅度十分明显,检验样本的BIAS都相对较大。相比Hopfield模型的BIAS,传统BP模型除了01-01和03-01存在几个检验样本BIAS较大之外,整体波动幅度较小,相对比较稳定。融合模型的BIAS波动均比较稳定。相比Hopfield模型和传统BP模型,融合模型在检验样本的BIAS相对靠近0值。
5 结语本文通过提取Wyoming大学提供的北半球120多个测站2010年中6 d(共753个气象探空数据)的对流层延迟“真值”,分析Hopfield模型、传统BP模型和融合模型的精度。结果表明,融合模型精度较Hopfield模型有显著提高。不仅证明了基于神经网络模型误差补偿技术应用于对流层延迟模型误差的可行性,同时也说明本文构建的融合模型精度较Hopfield模型和传统BP模型有明显改善。
| [1] |
Leandro R F, Langley R B, Santos M C. UNB3m_Pack: A Neutral Atmosphere Delay Package for Radiometric Space Techniques[J]. GPS Solutions, 2008, 12(1): 65-70 DOI:10.1007/s10291-007-0077-5
(  0) 0) |
| [2] |
Penna N, Dodson A, Chen W. Assessment of EGNOS Tropospheric Correction Model[J]. Journal of Navigation, 2001, 54(1): 37-55 DOI:10.1017/S0373463300001107
(  0) 0) |
| [3] |
李薇, 袁运斌, 欧吉坤, 等. 全球对流层天顶延迟模型IGGtrop的建立与分析[J]. 科学通报, 2012, 57(15): 1317-1325 (Li Wei, Yuan Yunbin, Ou Jikun, et al. A New Global Zenith Tropospheric Delay Model IGGtrop for GNSS Applications[J]. Chinese Science Bulletin, 2012, 57(15): 1317-1325)
(  0) 0) |
| [4] |
姚宜斌, 何畅勇, 张豹, 等. 一种新的全球对流层天顶延迟模型GZTD[J]. 地球物理学报, 2013, 56(7): 2218-2227 (Yao Yibin, He Changyong, Zhang Bao, et al. A New Global Zenith Tropospheric Delay Model GZTD[J]. Chinese Journal of Geophysics, 2013, 56(7): 2218-2227 DOI:10.6038/cjg20130709)
(  0) 0) |
| [5] |
Böhm J, Möller G, Schindelegger M, et al. Development of an Improved Empirical Model for Slant Delays in the Troposphere (GPT2w)[J]. GPS Solutions, 2015, 19(3): 433-441 DOI:10.1007/s10291-014-0403-7
(  0) 0) |
| [6] |
Hopfield H S. Two-Quartic Tropospheric Refractivity Profile for Correcting Satellite Data[J]. Journal of Geophysical Research Atmospheres, 1969, 74(18): 4487-4499 DOI:10.1029/JC074i018p04487
(  0) 0) |
| [7] |
Saastamoinen J. Atmospheric Correction for the Troposphere and Stratosphere in Radio Ranging Satellites[J]. Use of Artificial Satellites for Geodesy, 1972, 15(6): 247-251
(  0) 0) |
| [8] |
Black H D. An Easily Implemented Algorithm for the Tropospheric Range Correction[J]. Journal of Geophysical Research: Solid Earth, 1978, 83(B4): 1825-1828 DOI:10.1029/JB083iB04p01825
(  0) 0) |
| [9] |
朱明晨, 赵平, 陈伟荣. 基于BP神经网络的霍普菲尔德模型改进研究[J]. 测绘工程, 2016, 25(9): 26-30 (Zhu Mingchen, Zhao Ping, Chen Weirong. Improved Research for Hopfield Model Based on BP Neural Network[J]. Engineering of Surveying and Mapping, 2016, 25(9): 26-30)
(  0) 0) |
| [10] |
胡伍生, 张志伟. 模型误差补偿的神经网络方法研究[J]. 测绘科学, 2010, 35(增1)): 48-51 (Hu Wusheng, Zhang Zhiwei. Study on the Method for Compensating Model Error Based on Neutral Network[J]. Science of Surveying and Mapping, 2010, 35(S1): 48-51)
(  0) 0) |
| [11] |
丁士俊, 陶本藻. 自然样条半参数模型与系统误差估计[J]. 武汉大学学报:信息科学版, 2004, 29(11): 964-967 (Ding Shijun, Tao Benzao. Semiparametric Regression Model with Natural Spline and Systematic Error Estimation[J]. Geomatics and Information Science of Wuhan University, 2004, 29(11): 964-967)
(  0) 0) |
| [12] |
孙海燕, 吴云. 半参数回归与模型精化[J]. 武汉大学学报:信息科学版, 2002, 27(2): 172-174 (Sun Haiyan, Wu Yun. Semiparametric Regression and Model Refining[J]. Geomatics and Information Science of Wuhan University, 2002, 27(2): 172-174)
(  0) 0) |
| [13] |
高宁, 高彩云, 徐长海. 补偿最小二乘估计在确定高程异常中的应用[J]. 测绘科学, 2011, 36(1): 35-37 (Gao Ning, Gao Caiyun, Xu Changhai. Application of Penalized Least Squares Estimation in Height Anomaly[J]. Science of Surveying and Mapping, 2011, 36(1): 35-37)
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38


