为了快速实时估计卫星钟差,学者们提出采用相位历元差分方法消除模糊度参数,并结合非差伪距观测值,从而获取绝对卫星钟差。Bock等[1]利用基于相位历元差分的高采样率卫星钟差内插算法获得1 Hz的卫星钟差,但很耗时。Zhang等[2]运用2个并行线程生成高采样率的相对钟差以及低采样率的绝对钟差,从而得到1 Hz的钟差产品,当估计低采样率绝对钟差失败时,需要引入外部钟差基准。Ge等[3]在使用双线程估计高采样率钟差的同时,估计初始钟差基准,避免了外部基准的引入,但是需要初始钟差基准收敛到和伪距精度相当才能使用。
相位历元差分虽然可以得到较高采样率的相对卫星钟差,但是在初始阶段以及周跳发生时刻,仍需要通过非差模型得到绝对钟差基准。由于历元差分消除了模糊度参数,并不利于后续非差模糊度固定及相位硬件延迟特性研究[4]。卫星精密定轨与非差模糊度固定采用的是非差消电离层模型,可以一并估计卫星钟差、UPDs(相位硬件延迟)、ISBs等参数,能较好地保证产品间的一致性以及兼容性,例如法国CNES已通过这种方式提供相应的实时PPP服务[5]。
本文首先给出实时非差GPS卫星钟差估计流程以及策略;其次介绍了基于单观测值Kalman滤波的增益矩阵快速计算方法;最后基于OpenMP实现了Kalman滤波协方差快速更新。为了分析卫星钟差的精度以及计算效率,将估计的卫星钟差与IGS 30 s钟差产品进行对比,同时选取10个IGS站进行实时静态PPP以及动态PPP,并对比分析OpenMP单历元计算效率。
1 实时GPS卫星钟差估计模型 1.1 数学模型GPS消电离层组合观测方程为:
| $ \begin{array}{l} {\rm{PC = }}\rho {\rm{ + }}c{\rm{d}}{t_r}-c{\rm{d}}{t^s} + M\left( \theta \right) \cdot {T_w} + {\varepsilon _{{\rm{PC}}}}\\ {\rm{LC = }}\rho {\rm{ + cd}}{t_r}-c{\rm{d}}{t^s} + M\left( \theta \right) \cdot {T_w} + {\lambda _{{\rm{LC}}}}{B_{{\rm{LC}}}} + {\varepsilon _{{\rm{LC}}}} \end{array} $ | (1) |
式中,PC为伪距消电离层组合观测值,LC为载波消电离层组合观测值,ρ为卫星相位中心到接收机相位中心的几何距离,dtr为接收机钟差,dts为卫星钟差,M(θ)为对流层湿延迟投影函数,其与测站r到卫星s的高度角θ相关,Tw为对流层湿延迟,BLC为载波消电离层组合模糊度,λLC为消电离层组合载波波长,εPC、εLC分别为消电离层组合伪距及载波上的多路径、观测噪声等未模型化的误差。
实时卫星钟差需要估计的参数包括接收机钟差dtr、卫星钟差dts、天顶对流层延迟Tw以及消电离层浮点模糊度BLC。因为同时估计卫星轨道以及测站坐标对最后解算的卫星钟差精度相当[6],为了提升计算效率,本文事先通过IGS提供的Sinex周解文件固定测站坐标,用精密星历计算卫星轨道。接收机钟差dtr需要进一步说明,为了提升Kalman滤波的稳定性以及降低过程噪声[7],预处理过程中需要通过标准单点定位(SPP)计算粗略接收机钟差,然后从观测值中移除。
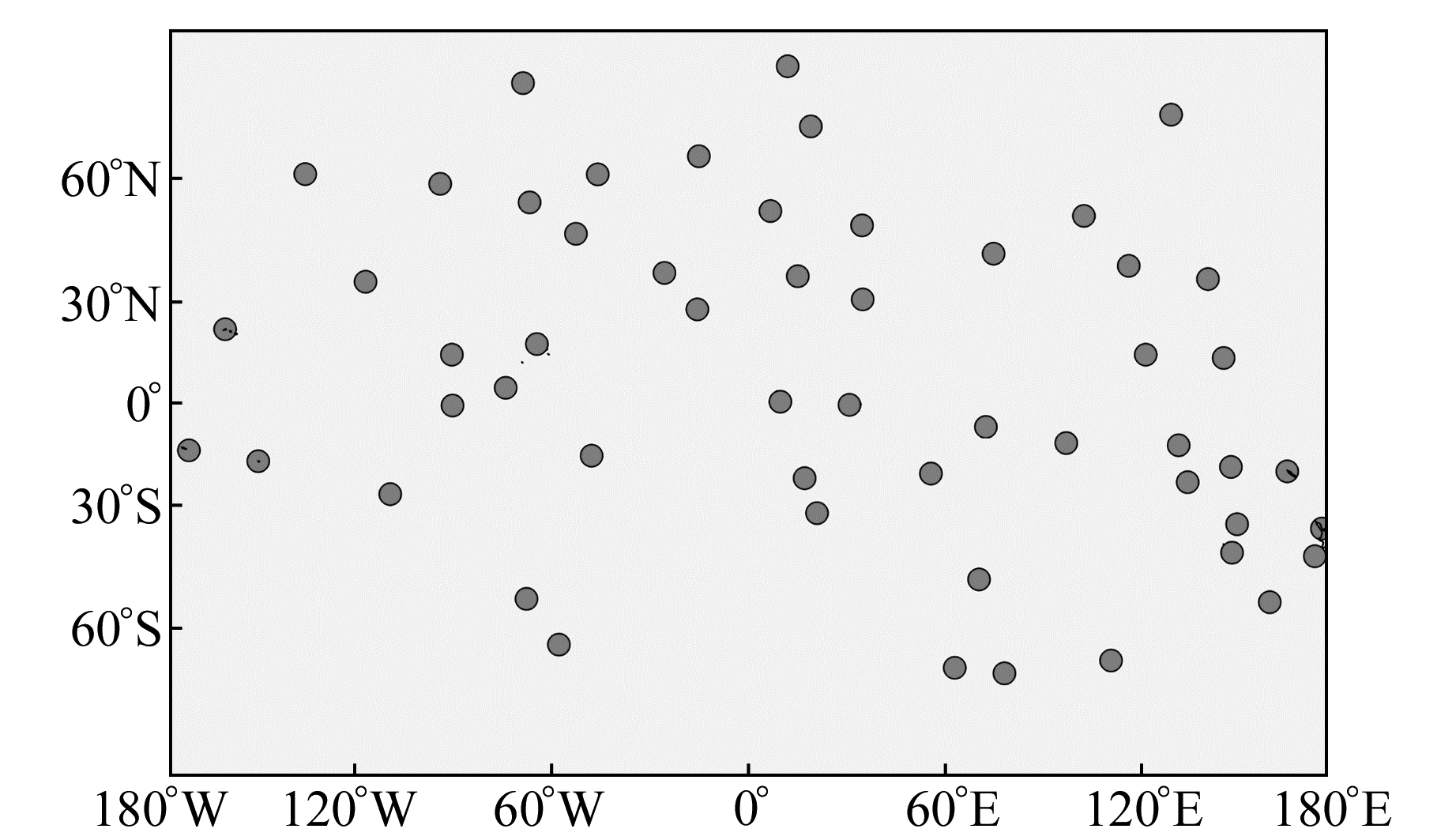
1.2 实时估计流程及策略为了模拟实时计算60 s采样率卫星钟差,均匀选取全球55个IGS跟踪站参与计算,见图 1。
|
图 1 卫星钟差实时估计的55个全球站分布 Fig. 1 Distribution for 55 reference stations for real time satellite clock estimation |
卫星钟差实时估计步骤如下:
1) 数据预处理。各项误差改正以及改正模型见表 1。对于处于地影的卫星,采用降低其观测值权重而不是直接删除卫星的策略,从而保持观测卫星的连续性。
|
|
表 1 实时卫星钟差估计策略 Tab. 1 Strategy for real time satellite clock estimation |
2) 单观测值Kalman滤波解算。为了解决实时卫星钟差估计方程秩亏问题,引入广播星历基准,通过约束所有有效卫星钟差和等于广播星历计算出的卫星钟差和来实现。滤波计算需要确定参数的随机模型,接收机钟差采用白噪声模型进行估计,对流层以及卫星钟差采用随机游走模型进行估计。模糊度参数作为常数进行估计,若发生周跳,模糊度需要重新初始化。
3) IGG-Ⅲ粗差探测。通过比较标准化残差vi以及验后单位权方差
表 1总结了本文实时卫星钟差估计的策略,图 2给出了实时估计的流程图。

|
图 2 实时卫星钟差估计流程图 Fig. 2 Workflow for real time satellite clock estimation |
| $ {\bar P_i} = \left\{ \begin{array}{l} {P_i}, \left| {{v_i}} \right| \le {k_0}{{\hat \sigma }_0}\\ \frac{{{k_0}{{\hat \sigma }_0}}}{{\left| {{v_i}} \right|}}{\left( {\frac{{{k_1}{{\hat \sigma }_0}-\left| {{v_i}} \right|}}{{{k_1}{{\hat \sigma }_0}-{k_0}{{\hat \sigma }_0}}}} \right)^2}, {k_0}{{\hat \sigma }_0} < \left| {{v_i}} \right| \le {k_1}{{\hat \sigma }_0}\\ 0, \left| {{v_i}} \right| > {k_1}{{\hat \sigma }_0} \end{array} \right. $ | (2) |
采用Kalman滤波估计实时卫星钟差时,需要知道待估参数的状态转移模型及观测方程:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{X}}_k} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k, k-1}}{\mathit{\boldsymbol{X}}_{k-1}} + {\mathit{\boldsymbol{W}}_{k-1}}\\ {\mathit{\boldsymbol{L}}_k} = {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{X}}_k} + {\mathit{\boldsymbol{V}}_k} \end{array} \right. $ | (3) |
式中,Xk为t(k)时刻的状态向量,Φk, k-1为从t(k-1)时刻到t(k)时刻的状态转移矩阵,Wk为过程噪声矩阵,Lk为观测值向量,Hk为设计矩阵,Vk为测量噪声矩阵。Wk及Vk需要满足均值为0的高斯白噪声特性:
| $ \left\{ \begin{array}{l} E\left( {{\mathit{\boldsymbol{W}}_i}} \right) = 0, {\mathop{\rm cov}} \left( {{\mathit{\boldsymbol{W}}_i}, {\mathit{\boldsymbol{W}}_j}} \right) = {\delta _{ij}}{\mathit{\boldsymbol{Q}}_i}\\ E\left( {{\mathit{\boldsymbol{V}}_i}} \right) = 0, {\mathop{\rm cov}} \left( {{\mathit{\boldsymbol{V}}_i}, {\mathit{\boldsymbol{V}}_j}} \right) = {\delta _{ij}}{\mathit{\boldsymbol{R}}_i}\\ {\mathop{\rm cov}} \left( {{\mathit{\boldsymbol{W}}_i}, {\mathit{\boldsymbol{V}}_j}} \right) = 0 \end{array} \right., {\delta _{ij}} = \left\{ \begin{array}{l} 1, i = j\\ 0, i \ne j \end{array} \right. $ | (4) |
式中,R及Q为测量噪声协方差矩阵和过程噪声协方差矩阵。精密钟差估计的状态向量形式为:
| $ \mathit{\boldsymbol{X}} = {\left[{{{(c{\rm{d}}{t_r})}_{1 \times m}}, {{(c{\rm{d}}{t^s})}_{1 \times n}}, {{({T_w})}_{1 \times m}}, {B_t}} \right]^{\rm{T}}} $ | (5) |
式中,m为测站个数,n为观测卫星个数,t为模糊度参数个数。
状态转移矩阵及过程噪声协方差矩阵为:
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k, k- 1}} = \left[{\begin{array}{*{20}{c}} {{0_{m \times m}}}&{{0_{1 \times n}}}&{{0_{1 \times m}}}&{{0_{1 \times t}}}\\ {{0_{n \times 1}}}&{{\mathit{\boldsymbol{I}}_{n \times n}}}&{{0_{n \times m}}}&{{0_{n \times t}}}\\ {{0_{m \times 1}}}&{{0_{m \times n}}}&{{\mathit{\boldsymbol{I}}_{m \times m}}}&{{0_{m \times t}}}\\ {{0_{t \times 1}}}&{{0_{t \times n}}}&{{0_{t \times m}}}&{{0_{t \times t}}} \end{array}} \right] $ | (6) |
| $ \begin{array}{l} {\mathit{\boldsymbol{Q}}_k} = \\ \left[{\begin{array}{*{20}{c}} {\sigma _{{\rm{d}}{t_r}}^2 \cdot {\mathit{\boldsymbol{I}}_{m \times m}}}&{{0_{1 \times n}}}&{{0_{1 \times m}}}&{{0_{1 \times t}}}\\ {{0_{n \times 1}}}&{\sigma _{{\rm{d}}{t^s}}^2 \cdot \Delta t \cdot {\mathit{\boldsymbol{I}}_{n \times n}}}&{{0_{n \times m}}}&{{0_{n \times t}}}\\ {{0_{m \times 1}}}&{{0_{m \times n}}}&{\sigma _{{T_w}}^2 \cdot \Delta t \cdot {\mathit{\boldsymbol{I}}_{m \times m}}}&{{0_{m \times t}}}\\ {{0_{t \times 1}}}&{{0_{t \times n}}}&{{0_{t \times m}}}&{{0_{t \times t}}} \end{array}} \right] \end{array} $ | (7) |
Kalman滤波的时间更新为:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{X}}_k^-= {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k, k-1}}{\mathit{\boldsymbol{X}}_{k-1}}\\ \mathit{\boldsymbol{P}}_k^ - = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k, k - 1}}{\mathit{\boldsymbol{P}}_{k - 1}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k, k - 1}^T + {\mathit{\boldsymbol{Q}}_k} \end{array} \right. $ | (8) |
测量更新为:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{X}}_k} = \mathit{\boldsymbol{X}}_k^-+ \mathit{\boldsymbol{K}}({\mathit{\boldsymbol{L}}_k}-{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{X}}_{k-1}})\\ {\mathit{\boldsymbol{P}}_k} = (\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{K}}{\mathit{\boldsymbol{H}}_k})\mathit{\boldsymbol{P}}_k^ - \end{array} \right. $ | (9) |
式中,K为增益矩阵,令矩阵Gk为:
| $ {\mathit{\boldsymbol{G}}_k} = \mathit{\boldsymbol{R}}_k^{-1} + {\mathit{\boldsymbol{H}}_k}\mathit{\boldsymbol{P}}_k^-\mathit{\boldsymbol{H}}_k^T $ | (10) |
式中,Rk-1为观测值协方差矩阵的逆矩阵,HkT为设计矩阵的转置,则:
| $ \mathit{\boldsymbol{K}} = \mathit{\boldsymbol{P}}_k^-\mathit{\boldsymbol{H}}_k^T\mathit{\boldsymbol{G}}_k^{-1} $ | (11) |
可以看到,整个滤波过程中,矩阵Gk需要求逆,而由于矩阵Gk维数等于观测值个数,假设选取50个测站,平均每个测站观测到10颗卫星,则矩阵Gk维数为1 000,直接求逆非常耗时。采用消电离层组合估计卫星钟差时,观测值间相互独立,因此能够逐观测值进行Kalman滤波,且其与批处理等价[10]。
当采用逐观测值更新时,观测值向量Lk变成标量lk,设计矩阵Hk从二维矩阵降维成行向量hk,同时矩阵Gk退化成标量gk,直接从时间复杂度为O(n3)的矩阵求逆变成时间复杂度为O(n)的逐观测值计算,其中n为观测值数量,并且避免了矩阵Gk求逆的数值不稳定以及奇异等问题。计算得到的增益矩阵K同样变成行向量k,整个测量更新过程变为:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{k}} = {g_k}{\mathit{\boldsymbol{M}}_k}\\ {\mathit{\boldsymbol{X}}_k} = \mathit{\boldsymbol{X}}_k^-+ \mathit{\boldsymbol{k}}({l_k}-{\mathit{\boldsymbol{h}}_k}{\mathit{\boldsymbol{X}}_{k-1}})\\ {\mathit{\boldsymbol{P}}_k} = \mathit{\boldsymbol{P}}_k^ - - \mathit{\boldsymbol{k}}{\mathit{\boldsymbol{M}}_k} \end{array} \right. $ | (12) |
其中,
| $ {\mathit{\boldsymbol{M}}_k} = \mathit{\boldsymbol{P}}_k^-{\mathit{\boldsymbol{h}}^{\rm{T}}}_k $ | (13) |
式中,hkT为设计矩阵转置,式(10)可写为:
| $ {g_k} = \sigma _k^2 + {\mathit{\boldsymbol{h}}_k}{\mathit{\boldsymbol{M}}_k} $ | (14) |
式中,σk为观测的标准差。
单观测值Kalman滤波虽然可以通过降低矩阵运算维数、避免大型矩阵求逆来提高计算效率,但如式(12)所示,逐个观测值更新过程中,每次都需要更新二维协方差矩阵,同样耗时。然而,从时间复杂度分析,对于逐观测值协方差更新,它的时间复杂度为O(nm2),其中m为未知参数个数,远少于观测值个数n。同时考虑到协方差矩阵的对称性,其更新时间能够减半,因此单观测值Kalman滤波的计算效率理论上比批处理计算效率高。
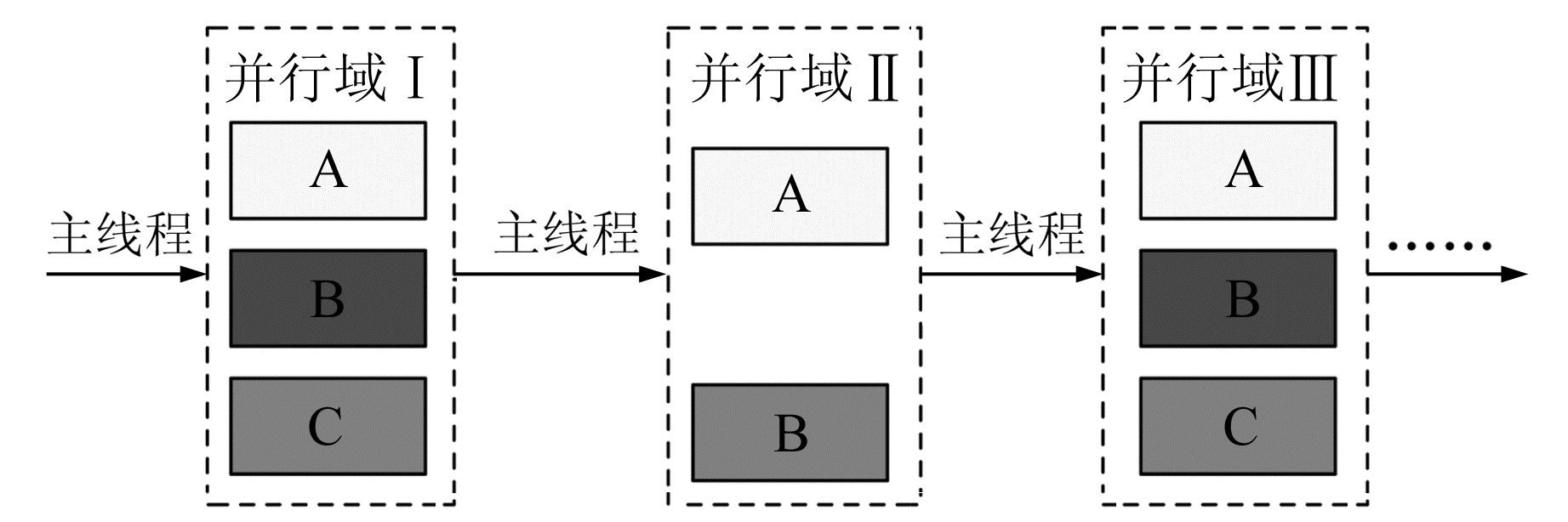
2.2 基于OpenMP的协方差更新OpenMP是基于线程的并行编程模型,采用Fork-Join并行方式执行。这种方式下,程序开始于一个主线程,当遇到并行区域,创建线程队列,将代码放到队列中执行,计算完毕后中断或者同步回到主线程执行。整个并行流程见图 3。
|
图 3 OpenMP并行原理图 Fig. 3 OpenMP working principle |
OpenMP的并行化是通过使用嵌入到C/C++或者Fortran源代码中的编译制导语句来实现的。基本格式为:
制导标识符 制导名称 [Clause, ]
以C/C++为例,制导标示符为#pragma omp;制导名称有parallel、for、section等;子句用来说明并行域的附加信息,如privared、shared、reduction、copyin等。
为进一步加快协方差更新效率,同时考虑其对称性,对于任意元素(i, j)有如下更新过程:
| $ {P_k}(i, j) = {P_k}(j, i) = P_k^-(i, j)-k(i){M_k}(j), j \ge i $ | (15) |
因此,对于协方差矩阵Pk的任意数量的行向量更新过程是彼此独立的,即可以将多个行更新在OpenMP并行域中完成,以加快其更新速度。
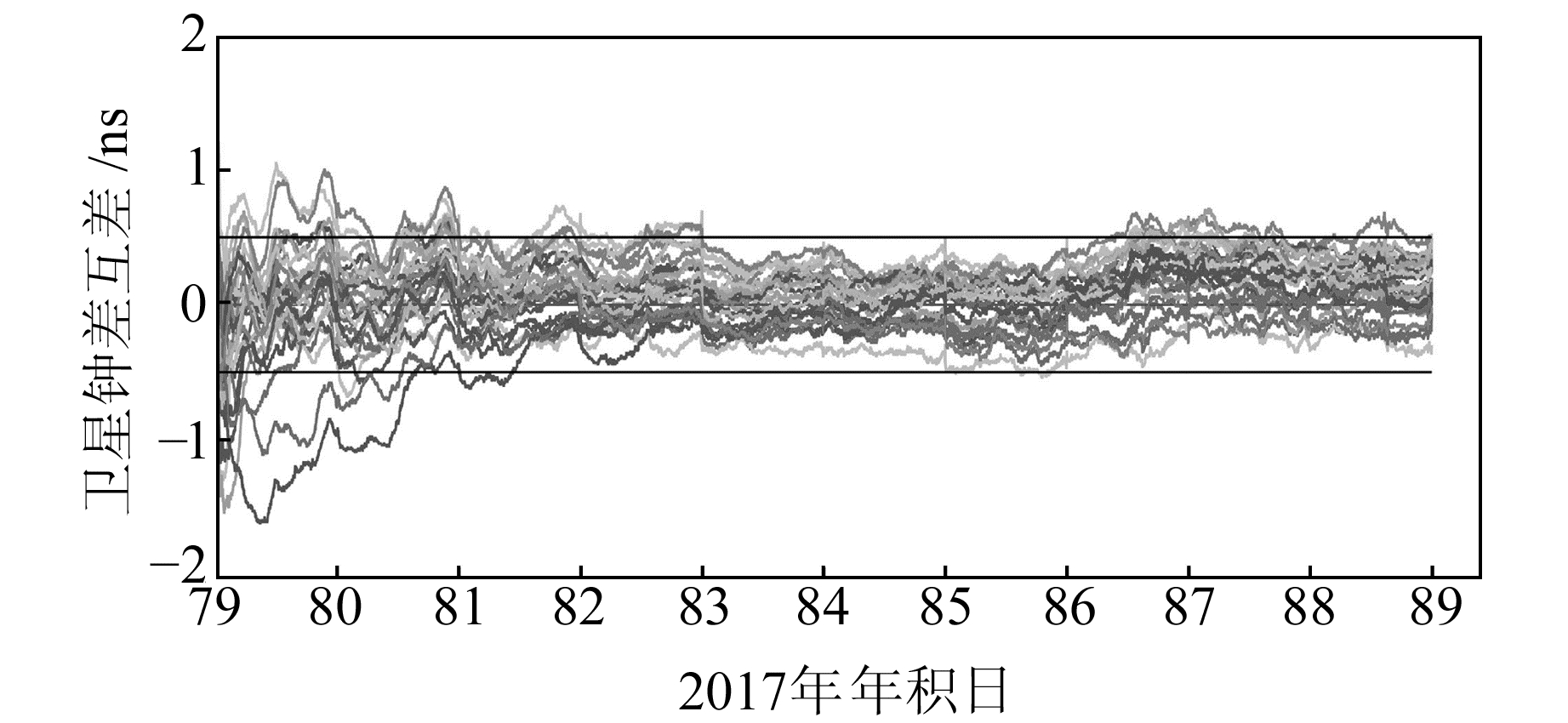
3 实验结果分析 3.1 IGS 30 s钟差比较为了分析实时钟差估计结果的精度,将其与IGS 30 s采样率的卫星钟差进行二次差比较[11],即选择一颗参考卫星,其他卫星减去参考卫星的钟差来消除基准不同造成的差异,然后将消除基准的钟差再作差得到钟差差异(图 4)。
|
图 4 估计实时卫星钟差与IGS 30 s钟差比较结果 Fig. 4 Comparison with IGS final 30's clock (采样率60 s,参考卫星为G10) (the rate is 60 s and reference satellite is G10) |
从图 4看出,所有卫星钟差的差异都在0.5 ns内,说明实时卫星钟差估计结果和IGS的钟差产品保持一致。由于初始历元没有引入卫星钟差初值,同时模糊度采用浮点方式估计,因此有一个比较长时间的收敛过程。但是对于G20等少数卫星,为了顾及实时性,在进行验后残差分析时,迭代次数超过预设最大迭代次数,没能很好地控制质量差的观测值的影响,势必导致收敛过程更长。与此同时,卫星轨道天与天间的差异会引起卫星钟差的跳跃,从图 4可以看出,这种差异非常小,量级小于0.1 ns。
表 2给出全部GPS卫星实时钟差的RMS,由于G07卫星在2017年第82天不可用,因此在处理时不估计其钟差。从表 2可以看出,大部分卫星钟差的RMS值在0.2 ns内。由于统计RMS并非从收敛后开始,因此可以看到少部分卫星的RMS偏大,特别是G20。
|
|
表 2 实时GPS卫星钟差RMS Tab. 2 RMS for real-time GPS satellite clocks |
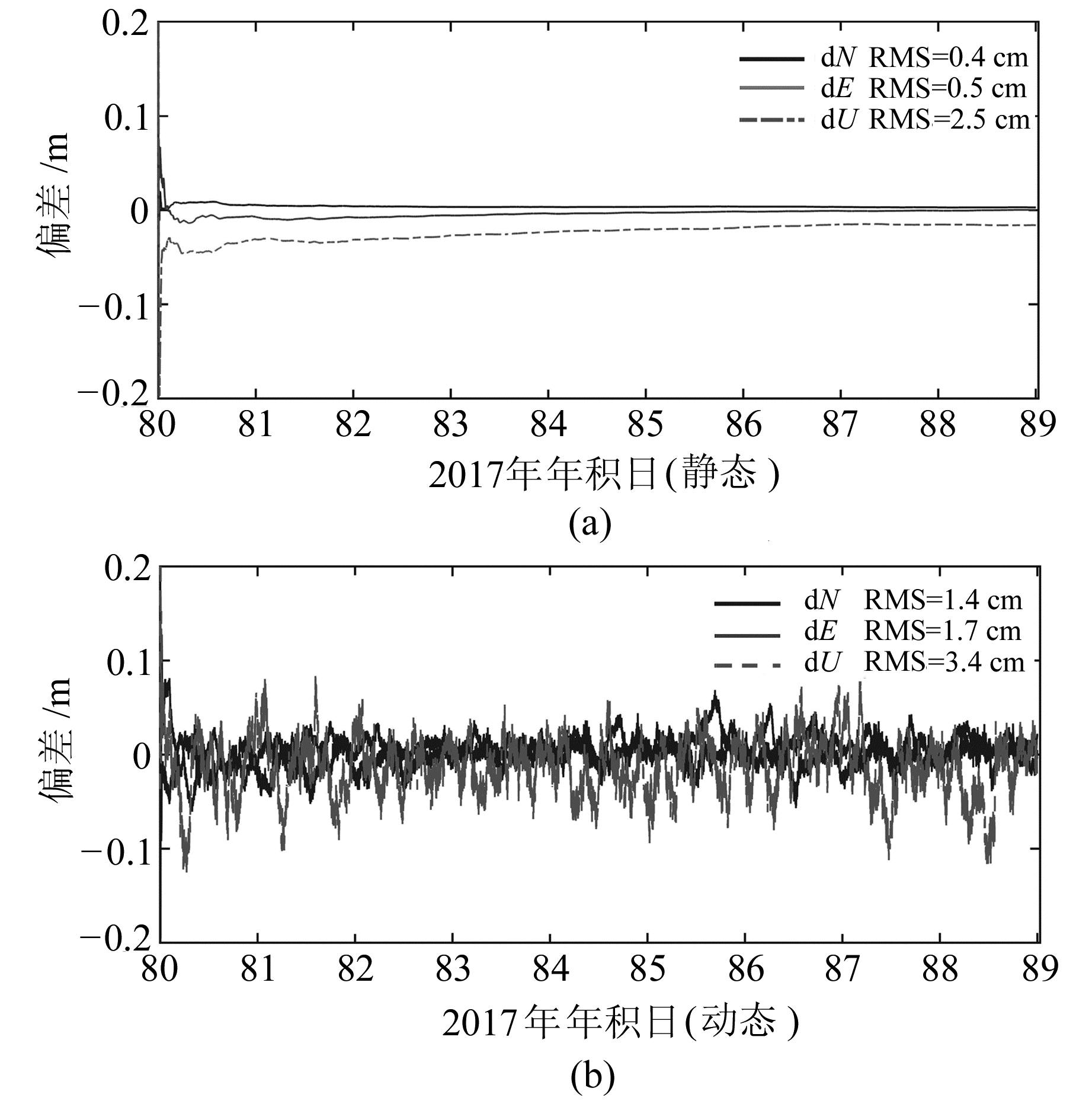
由于2017年第79天存在实时钟差收敛过程,因此选择第80~89天60 s实时解算的卫星钟差以及10个未参与解算的IGS跟踪站,分别进行实时静态和模拟动态精密单点定位。上述2种精密单点定位都是采用消电离层组合模型,同时模糊度采用浮点解,轨道采用IGS提供的超快速轨道。实时静态将测站坐标固定成常数,而模拟动态定位时将测站坐标当成白噪声进行估计,并且将解算结果与IGS提供的测站坐标周解进行比较。图 5给出了测站STK2在静态以及模拟动态情况下3个方向(N、E、U)上的偏差。
|
图 5 测站STK2静态以及模拟动态精密单点定位结果 Fig. 5 Real-time PPP in static and kinematic solutions for station STK2 |
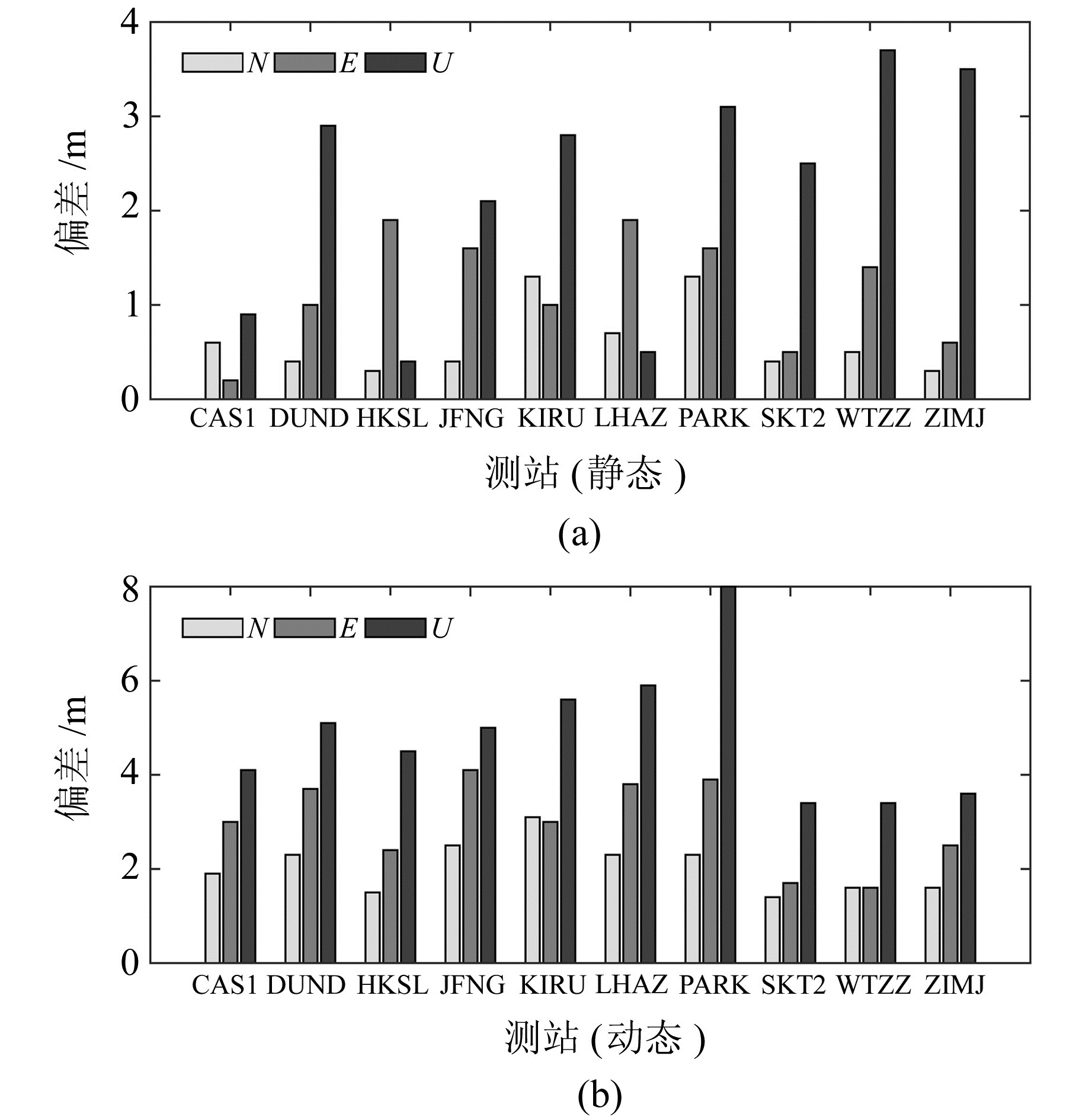
从图 5可以看出,由于初始测站坐标不准确,因此存在收敛过程,并且模拟动态PPP的收敛时间长于静态情况,两者收敛到cm级定位精度大约需要10~20 min,和传统的事后PPP收敛时间基本一致。随着时间的推移,2种定位模式的精度都趋于稳定。图 6总结了10个IGS跟踪站静态以及模拟动态PPP的结果,可以看出,实时静态PPP水平方向的精度优于2 cm,高程方向精度在2~4 cm范围内;而模拟动态的结果稍差于静态,水平方向的精度在2~4 cm的范围内,高程方向精度在4~6 cm。由于测站PARK观测数据质量不好,同时在第88天存在数据缺失,因此其静态以及模拟动态定位结果比较差,但能够满足实时PPP精度需求。
|
图 6 2017年第80到第89天10个非解算IGS跟踪站静态以及模拟动态PPP定位结果 Fig. 6 Real-time PPP in static and kinematic solutions for 10 IGS stations from day 80 to day 89 in 2017 |
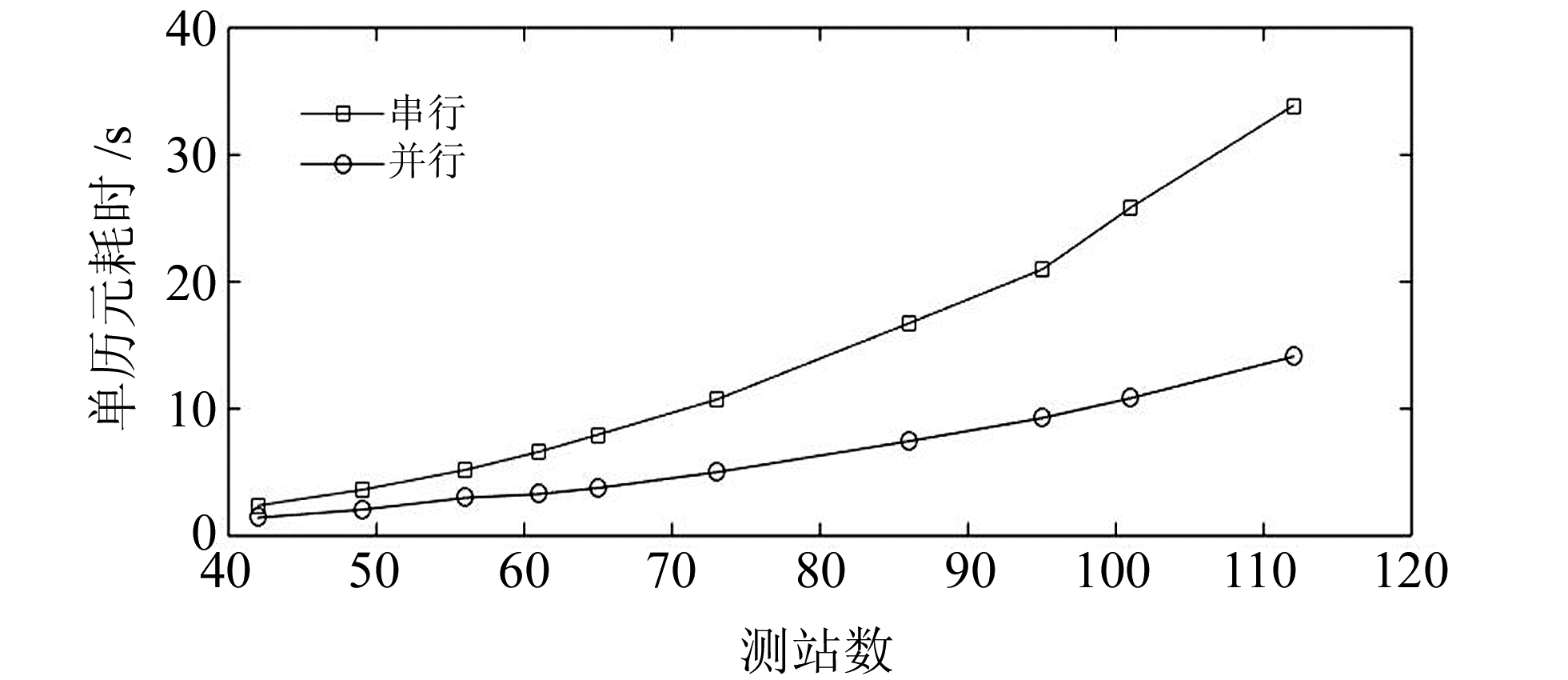
为了比较采用OpenMP前后实时钟差估计的效率,统计2017年第79天到89天60 s钟差单历元解算平均耗时随测站数的变化情况,结果见图 7。
|
图 7 OpenMP前后单历元解算时间随测站数变化 Fig. 7 Time cost for each epoch before and after using OpenMP |
从图 7可以看出,55个测站参与计算,串行模式下单历元耗时大约6 s, 并行模式下平均4 s,随着测站数量的增加,并行模式下单历元耗时明显小于串行模式。与此同时,并行模式实时卫星钟差估计耗时对测站数量的敏感程度低,非常适于密集参考站情况下的实时卫星钟差估计。
需要说明的是,上述统计结果是在8线程并行计算环境下得到的,当并行线程数量变多,单历元解算的速度会有更大提升。
4 结语本文提出一种高效稳健的非差GPS卫星钟差实时估计方法,避免了Kalman滤波过程中求解增益矩阵需要对大型矩阵求逆的问题,保证了效率以及数值稳定,同时通过OpenMP技术显著加快了单观测值Kalman滤波过程中协方差更新的速度。实验表明,估计钟差的结果和IGS 30 s钟差产品的差异在0.5 ns范围内。同时8线程并行解算,55个参考站参与的前提下,单历元耗时4 s,相比串行效率提升1/3,实时PPP静态水平方向精度优于2 cm,高程方向精度在2~4 cm,实时PPP动态水平方向精度在2~4 cm,高程方向精度在4~6 cm,说明实时钟差结果能够满足实时PPP精度要求。
基于OpenMP的GPS卫星钟差方法适用于非差观测模型,有利于今后实现GPS卫星轨道和钟差同时估计,可有效降低软件设计的复杂度。此外还可以将非差模糊度固定也纳入到模型中,具有很好的可扩展性。
| [1] |
Bock H, Dach R, Jäggi A, et al. High-Rate GPS Clock Corrections from CODE: Support of 1 Hz Applications[J]. Journal of Geodesy, 2009, 83(11): 1083 DOI:10.1007/s00190-009-0326-1
(  0) 0) |
| [2] |
Zhang X H, Li X X, Guo F. Satellite Clock Estimation at 1 Hz for Realtime Kinematic PPP Applications[J]. GPS Solutions, 2011, 15(4): 315-324 DOI:10.1007/s10291-010-0191-7
(  0) 0) |
| [3] |
Ge M R, Chen J P, Douša J, et al. A Computationally Efficient Approach for Estimating High-Rate Satellite Clock Corrections in Realtime[J]. GPS Solutions, 2012, 16(1): 9-17 DOI:10.1007/s10291-011-0206-z
(  0) 0) |
| [4] |
赵其乐, 戴志强, 王广兴, 等. 利用非差观测量估计北斗卫星实时精密钟差[J]. 武汉大学学报:信息科学版, 2016, 41(5): 686-691 (Zhao Qile, Dai Zhiqiang, Wang Guangxing, et al. Real-Time BDS Clock Estimation with the Undifferenced Observation[J]. Geomatics and Information Science of Wuhan University, 2016, 41(5): 686-691)
(  0) 0) |
| [5] |
Laurichesse D, Cerri L, Mercier F. Realtime Precise GPS Constellation and Clocks Estimation by Mean of a Kalman Filter[C]. ION GNSS, Institute of Navigation, Nashville, 2013
(  0) 0) |
| [6] |
李星星. GNSS精密单点定位及非差模糊度快速确定方法研究[D]. 武汉: 武汉大学, 2013 (Li Xingxing. Rapid Ambiguity Resolution in GNSS Precise Point Positioning[D]. Wuhan: Wuhan University, 2013) http://cdmd.cnki.com.cn/Article/CDMD-10486-1014135460.htm
(  0) 0) |
| [7] |
Hauschild A, Montenbruck O. Kalman-Filter-Based GPS Clock Estimation for Near Real-Time Positioning[J]. GPS Solutions, 2009, 13(3): 173-182 DOI:10.1007/s10291-008-0110-3
(  0) 0) |
| [8] |
Wu J T, Wu S C, Hajj G A, et al. Effects of Antenna Orientation on GPS Carrier Phase[C]. Astrodynamics, 1992
(  0) 0) |
| [9] |
Niell A E. Global Mapping Functions for the Atmosphere Delay at Radio Wavelengths[J]. Journal of Geophysical Research: Solid Earth, 1996, 101(B2): 3227-3246 DOI:10.1029/95JB03048
(  0) 0) |
| [10] |
Montenbruck O. Satellite Orbits Models Methods and Applications[M]. Berlin: Springer, 2005
(  0) 0) |
| [11] |
楼益栋, 施闯, 周小青, 等. GPS精密卫星钟差估计与分析[J]. 武汉大学学报:信息科学版, 2009, 34(1): 88-91 (Lou Yidong, Shi Chuang, Zhou Xiaoqing, et al. Realization and Analysis of GPS Precise Clock Products[J]. Geomatics and Information Science of Wuhan University, 2009, 34(1): 88-91)
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38

