现有算法理论不能完全抑制不确定性因素的影响。为提高参数估计的可靠性，需针对不确定性建立平差模型和平差准则，研究不确定度传播规律以及抑制不确定性的平差方法^[1]。将不确定性数值化、参数化并融入函数模型，建立不确定性平差模型，依据残差中不确定性传播规律，建立一种基于残差最大不确定性达到最小的平差准则，是一种处理不确定性数据的新方法^[2]。

当系数矩阵和观测向量均存在不确定性时，Ghaoui等^[3]使用F-范数(Frobenius范数)对其增广矩阵进行描述，建立基于F-范数的不确定性min-max平差准则，并采用二阶锥规划(second-order cone programing，SOCP)或先奇异值分解(singular value decomposition，SVD)、再SOCP(SVD-SOCP)或半定规划(semi-definite programming，SDP)的方法进行参数估计。Chandrasekaran等^[4-5]使用2-范数分别描述其不确定性，建立基于2-范数的不确定性min-max平差准则，釆用SVD和解算方程式的方法(SVD-解方程算法)进行参数估计。杨智慧等^[6]给出一种基于线性矩阵不等式(linear matrix inequality，LMI)的参数估计方法。宋迎春等^[1-2]将2-范数和F-范数描述的不确定性看作是不确定度，融入函数模型，建立相应的不确定性平差模型，依据残差中不确定性的传播规律，分别采用基于2-范数和F-范数的不确定性min-max平差准则解算对应模型，给出先SVD、再迭代计算的解算方法(SVD-迭代算法)，证明了迭代算法的收敛性问题。邹渤等^[7]把基于2-范数的不确定性平差模型理论运用到基坑沉降观测的AR模型中，抑制了不确定性因素对基坑沉降观测的不利影响。然而，SOCP、SVD-SOCP、SDP和SVD-迭代算法的解算过程都较复杂，且SVD-迭代算法不适用于迭代发散的情况。为此，本文在现有的SVD-迭代算法基础上，进一步研究基于F-范数的不确定性平差模型的另外2种算法：迭代不收敛时的SVD-解方程算法和迭代收敛时更为简单的直接迭代算法。

1 平差模型及准则

基于F-范数的不确定性平差模型为^[2]：

$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{L}}} + \Delta {\mathit{\boldsymbol{L}}} = {\rm{(}}{\mathit{\boldsymbol{A}}} + \Delta {\mathit{\boldsymbol{A}}}{\rm{)}}{\mathit{\boldsymbol{X}}}\\ \left\| {\Delta {\mathit{\boldsymbol{A}}}{\rm{ }}\Delta {\mathit{\boldsymbol{L}}}} \right\|{{\rm{ }}_F} \le \rho \end{array} \right. $

(1)

式中，L ∈ Rⁿ为观测向量，ΔL ∈ Rⁿ为L的不确定性，A ∈ R^n×m(n≥m)为系数矩阵，ΔA ∈ R^n×m为A的不确定性，X ∈ R^m为待求参数向量，[ΔA ΔL]是由不确定性ΔA和ΔL共同组成的增广矩阵，ρ可看作是对[ΔA ΔL]的一种度量，即不确定度^[2]，且ρ大于0，‖·‖_F表示F-范数。

针对模型(1)，可采用如下基于F-范数的不确定性min-max平差准则求解^[2]：

$ \mathop {{\rm{min}}}\limits_{{\mathit{\boldsymbol{\hat X}}}} \mathop {{\rm{max}}}\limits_{\left\| {\Delta {\mathit{\boldsymbol{A}}}{\rm{ }}\Delta {\mathit{\boldsymbol{L}}}} \right\|{{\rm{ }}_F} \le \rho } {\rm{ }}\left\| {{\rm{(}}{\mathit{\boldsymbol{A}}} + \Delta {\mathit{\boldsymbol{A}}}{\rm{)}}{\mathit{\boldsymbol{\hat X}}}-{\rm{(}}{\mathit{\boldsymbol{L}}} + \Delta {\mathit{\boldsymbol{L}}}{\rm{)}}} \right\|{_F} $

(2)

式中，符号“^”表示最优估值。该平差准则分为max(·)和min(·)内外2层，内层目标函数max(·)表示在系数矩阵A和观测向量L受不确定性ΔA和ΔL干扰且不确定度ρ已知的情况下，得到待求参数时残差的最大不确定度；外层目标函数min(·)表示使参数解中的不确定性达到最小化。该平差准则较为复杂，可将其等价转换为另一种简化形式后再进行解算。

先求内层目标函数max(·)的最大值，将ΔA和ΔL看成自变量，根据F-范数的性质可知，目标函数max(·)的极大值点就是最大值点，设其为(ΔA⁰, ΔL⁰)。当^[4]

$ \left[{\Delta {\mathit{\boldsymbol{A}}^0}\;\;\;\Delta {\mathit{\boldsymbol{L}}^0}} \right] = \frac{\mathit{\boldsymbol{u}}}{{\sqrt {\left\| {\mathit{\boldsymbol{\hat X}}} \right\|_F^2 + 1} }}\left[{{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}-1} \right] $

(3)

其中，

$ \mathit{\boldsymbol{u}} = \left\{ \begin{array}{l} \frac{{\rho \left( {\mathit{\boldsymbol{A\hat X}}-\mathit{\boldsymbol{L}}} \right)}}{{{{\left\| {\mathit{\boldsymbol{A\hat X}}-\mathit{\boldsymbol{L}}} \right\|}_F}}}, \mathit{\boldsymbol{A\hat X}} \ne \mathit{\boldsymbol{L}}\\ \mathit{\boldsymbol{I}}, \mathit{\boldsymbol{A\hat X = L}} \end{array} \right. $

(4)

时，目标函数max(·)可取得极大值，亦即最大值${\left\| {\mathit{\boldsymbol{A\hat X}}-\mathit{\boldsymbol{L}}} \right\|_F} + \rho \sqrt {\left\| {\mathit{\boldsymbol{\hat X}}} \right\|_F^2 + 1} $。所以，平差准则(2)可以等价转换为如下形式更为简单的min平差准则^[2]：

$ \mathop {\min }\limits_{\mathit{\boldsymbol{\hat X}}} \left\{ {{{\left\| {\mathit{\boldsymbol{A\hat X}}-\mathit{\boldsymbol{L}}} \right\|}_F} + \rho \sqrt {\left\| {\mathit{\boldsymbol{\hat X}}} \right\|_F^2 + 1} } \right\} $

(5)

该平差准则表示在给定的已知条件下，估计出一个最优参数解$\mathit{\boldsymbol{\hat X}}$，使得一个含有F-范数的一元函数在其全局定义域内取得最小值。

2 模型的解算方法

针对平差准则(5)，文献[2]给出了SVD-迭代算法，本文给出另外2种算法。

2.1 SVD-解方程算法

为了求解平差准则(5)目标函数的最小值，令

$ \mathit{\Gamma} \left( {\mathit{\boldsymbol{\hat X}}} \right) = {\left\| {\mathit{\boldsymbol{A\hat X}}-\mathit{\boldsymbol{L}}} \right\|_F} + \rho \sqrt {\left\| {\mathit{\boldsymbol{\hat X}}} \right\|_F^2 + 1} $

(6)

此时，问题(5)变为求解一个含有F-范数的一元函数Γ($\mathit{\boldsymbol{\hat X}}$)在其全局定义域$\mathit{\boldsymbol{\hat X}}$∈ R^m上的最小值。根据F-范数的性质可知，目标函数Γ($\mathit{\boldsymbol{\hat X}}$)在全局定义域内是连续可导的，且二阶导数大于0。所以，目标函数Γ($\mathit{\boldsymbol{\hat X}}$)的极小值就是其最小值。

由函数求自由极值的方法，对目标函数Γ($\mathit{\boldsymbol{\hat X}}$)求导，并令其等于零向量，有：

$ \frac{{\partial \Gamma {\rm{(}}{\mathit{\boldsymbol{\hat X}}}{\rm{)}}}}{{\partial {\mathit{\boldsymbol{\hat X}}}}} = \frac{{{{\mathit{\boldsymbol{A}}}^{\rm{T}}}{\rm{(}}{\mathit{\boldsymbol{A\hat X}}}-{\mathit{\boldsymbol{L}}}{\rm{)}}}}{{{{\left\| {{\mathit{\boldsymbol{A\hat X}}}-{\mathit{\boldsymbol{L}}}} \right\|}_F}}} + \frac{{\rho {\mathit{\boldsymbol{\hat X}}}}}{{\sqrt {\left\| {{\mathit{\boldsymbol{\hat X}}}} \right\|_F^{\rm{2}} + 1} }} = 0 $

(7)

整理得：

$ {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A\hat X}}-{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}} =-\hat \nu \mathit{\boldsymbol{\hat X}} $

(8)

式中，$\hat \nu $为中间参数，其表达式为：

$ \hat \nu = \rho \frac{{{\rm{ }}{{\left\| {\mathit{\boldsymbol{A\hat X}}-\mathit{\boldsymbol{L}}} \right\|}_F}}}{{\sqrt {\left\| {\mathit{\boldsymbol{\hat X}}} \right\|_F^{\rm{2}} + 1} }} $

(9)

为解出$\mathit{\boldsymbol{\hat X}}$，需要先解得$\hat v$。对系数矩阵A进行SVD：

$ \mathit{\boldsymbol{A}} = \mathit{\boldsymbol{U}}\left[\begin{array}{l} \mathit{\boldsymbol{ \boldsymbol{\varSigma} }}\\ \bf{0} \end{array} \right]{\mathit{\boldsymbol{V}}^{\rm{T}}} $

(10)

式中，U ∈ R^n×n、V ∈ R^m×m均为正交矩阵，Σ =diag(σ₁, σ₂, …, σ_m)为对角矩阵，且对角元素满足σ₁≥σ₂…≥σ_m>0，这是A的全部奇异值。再对向量(U^T L)进行分块：

$ \left[\begin{array}{l} {\mathit{\boldsymbol{L}}_1}\\ {\mathit{\boldsymbol{L}}_2} \end{array} \right] = {\mathit{\boldsymbol{U}}^{\rm{T}}}\mathit{\boldsymbol{L}} $

(11)

式中，L₁∈ R^m、L₂∈ R^n－m均为向量(U^TL)的子向量。

将式(10)、(11)代入式(8)，得到待求参数$\mathit{\boldsymbol{\hat X}}$的另一种等价表达式：

$ \mathit{\boldsymbol{\hat X}} = \mathit{\boldsymbol{V}}{{\rm{(}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^2} + \hat \nu {\mathit{\boldsymbol{I}}_m}{\rm{)}}^{-1}}\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}{\mathit{\boldsymbol{L}}_{\rm{1}}} $

(12)

将式(12)等号两边同时取F-范数，并根据F-范数的正交不变性以及对角矩阵与对角矩阵的可交换性得：

$ {\left\| {\mathit{\boldsymbol{\hat X}}} \right\|_F} = {\left\| {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}{{{\rm{(}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^2} + \hat \nu {\mathit{\boldsymbol{I}}_m}{\rm{)}}}^{-1}}{\mathit{\boldsymbol{L}}_{\rm{1}}}{\rm{ }}} \right\|_F} $

(13)

将式(10)~(12)代入向量($\mathit{\boldsymbol{L}}-\mathit{\boldsymbol{A\hat X}}$)，并取F-范数：

$ \begin{array}{l} {\left\| {\mathit{\boldsymbol{L}}-\mathit{\boldsymbol{A\hat X}}} \right\|_F} = \\ \sqrt {\left\| {{\mathit{\boldsymbol{L}}_2}} \right\|_F^2 + {{\hat v}^2}\left\| {\left( {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^2} + \hat v{\mathit{\boldsymbol{I}}_m}} \right){\mathit{\boldsymbol{L}}_1}} \right\|_F^2} \end{array} $

(14)

将式(13)、(14)代入式(9)，得$\hat v$的另一种等价表达式：

$ \hat v = \rho \frac{{\sqrt {\left\| {{\mathit{\boldsymbol{L}}_2}} \right\|_F^2 + {{\hat v}^2}\left\| {\left( {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^2} + \hat v{\mathit{\boldsymbol{I}}_m}} \right){\mathit{\boldsymbol{L}}_1}} \right\|_F^2} }}{{\sqrt {\left\| {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}{{\left( {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^2} + \hat v{\mathit{\boldsymbol{I}}_m}} \right)}^{-1}}{\mathit{\boldsymbol{L}}_1}} \right\|_F^2 + 1} }} $

(15)

将式(15)的等号两边同时平方，整理得：

$ \begin{array}{l} {{\hat v}^2}\left( {\mathit{\boldsymbol{L}}_1^{\rm{T}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^2}{{\left( {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^2} + \hat v{\mathit{\boldsymbol{I}}_m}} \right)}^{-2}}{\mathit{\boldsymbol{L}}_1} + 1} \right) = \\ {\rho ^2}\left( {\left\| {{\mathit{\boldsymbol{L}}_2}} \right\|_F^2 + {{\hat v}^2}\mathit{\boldsymbol{L}}_1^{\rm{T}}{{\left( {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^2} + \hat v{\mathit{\boldsymbol{I}}_m}} \right)}^{-2}}{\mathit{\boldsymbol{L}}_1}} \right) \end{array} $

(16)

将式(16)等号两边同时除以${\hat v^2}$，整理得：

$ \begin{array}{l} \mathit{\boldsymbol{L}}_1^{\rm{T}}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^2}-{\rho ^2}{\mathit{\boldsymbol{I}}_m}} \right){\left( {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^2} + \hat v{\mathit{\boldsymbol{I}}_m}} \right)^{-2}}{\mathit{\boldsymbol{L}}_1}-\\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{{{\rho ^2}}}{{{{\hat v}^2}}}\left\| {{\mathit{\boldsymbol{L}}_2}} \right\|_F^2 = - 1 \end{array} $

(17)

为求解式(17)中$\hat v$，以ν为自变量，引入函数：

$ \begin{array}{l} \varphi \left( v \right) = \mathit{\boldsymbol{L}}_1^{\rm{T}}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^2}-{\rho ^2}{\mathit{\boldsymbol{I}}_m}} \right){\left( {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^2} + v{\mathit{\boldsymbol{I}}_m}} \right)^{-2}}{\mathit{\boldsymbol{L}}_1}-\\ \frac{{{\rho ^2}}}{{{v^2}}}\left\| {{\mathit{\boldsymbol{L}}_2}} \right\|_F^2 + 1 \end{array} $

(18)

令φ(ν)=0，可解得唯一的正实数根，即为所求的$\hat v$。此时，将$\hat v$代入式(8)，即得待求参数估值$\mathit{\boldsymbol{\hat X}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}} + \hat v{\mathit{\boldsymbol{I}}_m}} \right)^{-1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}}$。

2.2 直接迭代算法

联合式(8)、(9)可知，等号两边都含有待求参数$\mathit{\boldsymbol{\hat X}}$，可直接采用迭代算法对其进行求解，步骤如下：

1) 给定中间参数的初始值${\hat v^{\left( 0 \right)}} = 0$，代入式(8)，得到待求参数初始值为：

$ {\mathit{\boldsymbol{\hat X}}^{\left( 0 \right)}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)^{-1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}} $

(19)

2) 用步骤1)得到参数估值${\mathit{\boldsymbol{\hat X}}^{\left( i \right)}}$和已知值代入式(9)，得：

$ {\hat v^{\left( {i + 1} \right)}} = \rho \frac{{{{\left\| {\mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{\hat X}}}^{\left( i \right)}}-\mathit{\boldsymbol{L}}} \right\|}_F}}}{{\sqrt {\left\| {{{\mathit{\boldsymbol{\hat X}}}^{\left( i \right)}}} \right\|_F^2 + 1} }} $

(20)

然后，将其再次代入式(8)，解得待求参数估值为：

$ {\mathit{\boldsymbol{\hat X}}^{\left( {i + 1} \right)}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}} + {{\hat v}^{\left( {i + 1} \right)}}{\mathit{\boldsymbol{I}}_m}} \right)^{-1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}} $

(21)

式中，I_m为m阶单位矩阵。

3) 重复步骤2)，直到满足${\left\| {{{\mathit{\boldsymbol{\hat X}}}^{\left( {i + 1} \right)}}-{{\mathit{\boldsymbol{\hat X}}}^{\left( i \right)}}} \right\|_F} < \varepsilon $(ε为迭代终止条件的阈值)，计算结束。

直接迭代算法既没有用到SVD，也没有涉及解算方程式，简化了整个求解过程，便于编程计算。算例表明，当ρ很小时，迭代是收敛的；当ρ很大时，迭代不一定收敛。

3 算例分析

本节中算例都基于相同的计算平台。笔记本电脑型号为Dell Inspiron 15-5559，CPU型号为Intel(R)Core(TM)i7-6500U，主频为2.50 GHz，随机存取存储器为8.00 GB，操作系统为Windows 10 Home Basic，计算软件为Matlab R2012a(7.14.0.739)。设定系统误差为常数s，随机误差(由函数normrnd产生、期望为0、标准差为σ)，粗差为g，ε=10^－12。

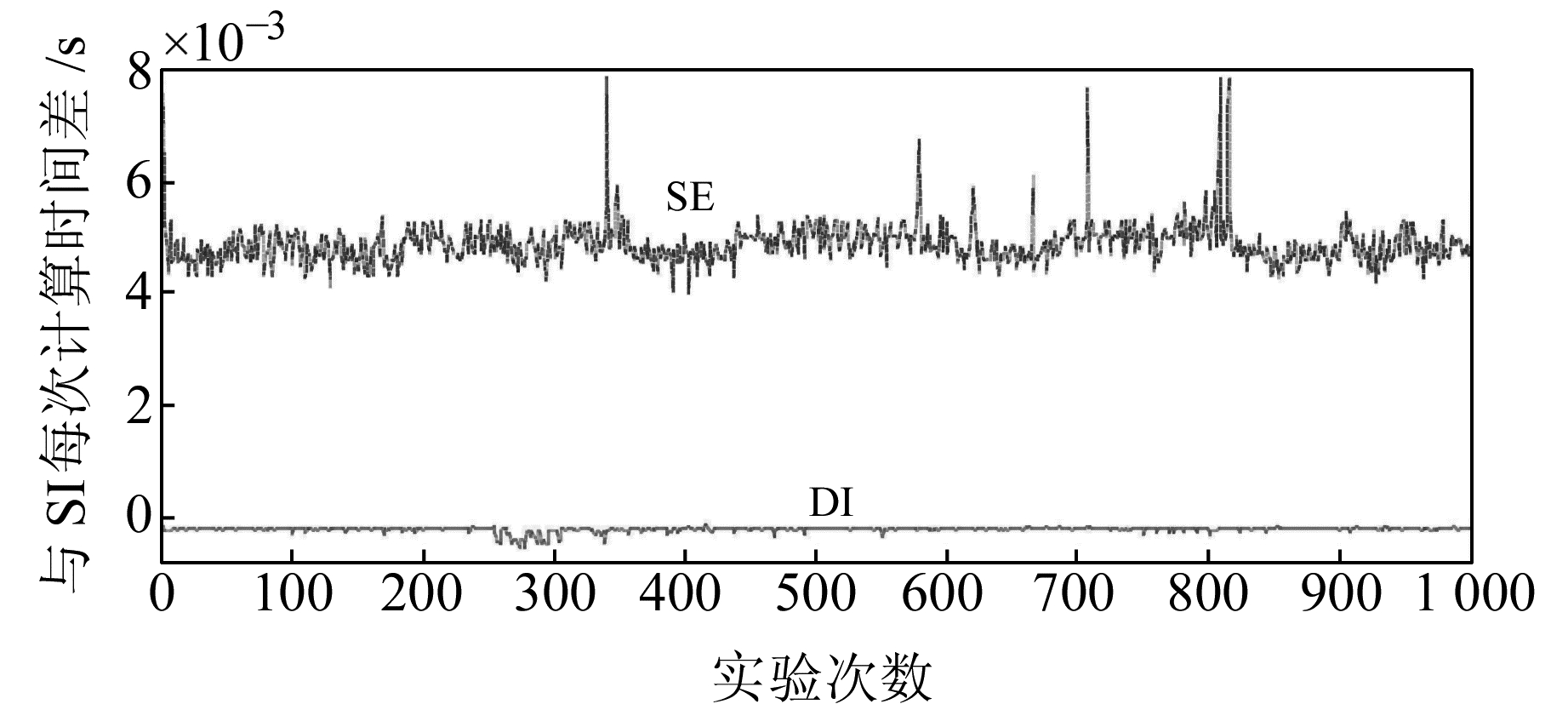
3.1 二元线性拟合

为分析本文所给2种算法的正确性和解算效率，考虑二元线性函数模型L = AX。假设拟合参数真值为X=[5.132 6 －2.003 9]^T，给定一组系数矩阵真值A，由此生成一组观测向量真值L，模拟真值见表 1。给A和L同时加入系统误差(s=0.10)、随机误差(μ=0，σ=0.20)，给第6个数据的所有分量加入粗差(g=0.30)，使其满足‖ΔA ΔL‖_F≤ρ=1.30，共模拟1 000次，产生1 000组同时含有这3种误差的数据。分别釆用文献[2]给出的SVD-迭代算法(SI)、本文给出的SVD-解方程算法(SE)和直接迭代算法(DI)对其进行参数估计。将每种算法各自计算1 000次得到拟合参数估值的均值和总计算时间，SE和DI得到的迭代次数均值列于表 2。图 1是每次SE和DI分别与SI计算的时间差。

从表 2可知，由SE、DI估计的拟合参数与SI的完全相同，验证了SE和DI的正确性，且3种算法具有等价性。

从表 2可知，DI迭代次数的均值比SI的小，说明DI的收敛速度更快；SE计算1 000次耗费的总时间最多，DI的最少，说明SE计算的时间效率最低，DI的最高。从图 1可知，SE与SI每次计算的时间差都大于0，而DI与SI每次计算的时间差都小于0，说明SE每次计算的时间效率都最低，而DI的都最高。这主要因为，SE的解算方程式比SI的迭代算法更为复杂，需消耗更多的CPU计算时间；DI无需SVD，且迭代次数比SI的少，消耗的CPU计算时间会更少。

3.2 沉降观测AR模型

在沉降观测值中，经常存在一些不确定性，其统计信息和概率分布函数难以确定，可釆用不确定性理论进行数据处理^[7]。以文献[8]中某建筑物某时段定期进行36次沉降观测中序数为4~36的高程值为例进行分析(表 3)。选取序数为4~27的沉降值建模，对序数为28~36的沉降值进行预测。由贝叶斯信息准则确定模型阶数为p=3。

自回归AR(p)模型为^[9]：

$ {x_t} = {\xi _1}{x_{t-1}} + {\xi _2}{x_{t-2}} + \cdots + {\xi _p}{x_{t-p}} + {e_t} $

(22)

式中，x_t为第t期的沉降值，ξ_i(i=0，1，2，…，p)为自回归系数，p为自回归模型的阶数，e_t为正态白噪声。

算例中的不确定度ρ未知，可先使用总体最小二乘(total least squares，TLS)平差准则计算出$\Delta \mathit{\boldsymbol{\hat A}}$和$\Delta \mathit{\boldsymbol{\hat L}}$，再将其作为不确定度ρ融入不确定性平差模型进行解算^[2-3]。釆用文献[10]的TLS平差准则，计算得${\left\| {\Delta \mathit{\boldsymbol{\hat A}}\;\;\;\Delta \mathit{\boldsymbol{\hat L}}} \right\|_F}$=2.933 47，所以取ρ=2.933 5，从而建立如下基于F-范数的不确定性平差模型：

$ \left\{ \begin{array}{l} \mathit{\boldsymbol{L}} + \Delta \mathit{\boldsymbol{L}} = \left( {\mathit{\boldsymbol{A}} + \Delta \mathit{\boldsymbol{A}}} \right)\mathit{\boldsymbol{X}}\\ {\left\| {\Delta \mathit{\boldsymbol{A}}\;\;\;\;\Delta \mathit{\boldsymbol{L}}} \right\|_F} \le 2.933\;5 \end{array} \right. $

(23)

式中，L=[x₂ x₃ … x₁₆]^T，A=[x₁ x₂ … x₁₅]^T，X等于ξ₁。

分别釆用基于F-范数的不确定性min-max平差准则(ULS)的3种算法(SI、SE和DI)解算模型(23)，并独立重复运行1 000次，统计总计算时间。此外，还釆用文献[11]的最小二乘(least squares，LS)平差准则进行参数估计。将计算得到的自回归系数代入自回归AR(p)模型(22)，对序数为28~36的沉降值进行预测。

表 4为SI、SE和DI平差计算的结果。由SE和DI计算得到的自回归系数与SI的完全相同，再次验证了SE和DI的正确性，以及这3种算法的等价性；DI的迭代次数比SI的少，再次说明DI的收敛速度更快；SE计算1 000次的总时间最多，而DI的最少，再次说明SE计算的时间效率最低，而DI的最高。

表 5为ULS、LS和TLS 3种平差准则得到的预测值与实测值的比较。可以看出，由ULS得到的预测值与实测值偏差序列的F-范数最小，验证了其预测结果的有效性。

4 结语

针对现有算法的不足，本文基于F-范数的不确定性平差模型，给出SVD-解方程算法和直接迭代算法，并推导其解算公式。通过二元线性拟合及沉降观测AR模型的算例，并与现有算法进行对比分析，得到以下结论：

1) SVD-解方程算法和直接迭代算法是正确可行的，且与SVD-迭代算法具有等价性。

2) 当迭代不收敛时，可釆用SVD-解方程算法，但涉及概念较多，解算过程较复杂，计算效率较低。

3) 当迭代收敛时，更适宜釆用直接迭代算法，该算法无需SVD，解算过程简单，易于编程计算，迭代次数更少，解算效率更高。