2. 中国科学院大学,北京市玉泉路甲19号,100049;
3. 中国科学院测量与地球物理研究所,武汉市徐东大街340号,430077
随着时代的发展,高精度重力梯度数据的重要性逐渐体现出来,同时也诞生了不同类型的以加速度计为核心的重力梯度测量系统。能够实现重力梯度全张量测量的主要有超导重力梯度仪、静电重力梯度仪和旋转加速度计重力梯度仪[1-3]。
1 结构分析基于差分加速度原理的不同,重力梯度仪结构特征为:旋转加速度计重力梯度仪使用的加速度计是线性的,即只能敏感某一方向上的加速度。一个圆盘上对称安置4个加速度计,为了获得重力梯度的全张量,需要在空间对称放置3个转盘[4],每个圆盘都要进行旋转。超导重力梯度仪单轴结构内的超导加速度计也是线性的,且没有旋转。为了测量重力梯度的全张量,除了三轴结构,还必须安装数个角加速度计来测量梯度张量中的非对角分量,以及消除角速度和角加速度带来的动态误差[1, 5-6]。静电重力梯度仪的加速度计单元是静电悬浮球,可以敏感3个自由度方向上的加速度,测量重力梯度全张量共需要6个加速度计,空间对称摆放。因其仅工作在室温零重力的太空状态,故目前仅用于卫星上[9]。
表 1给出几种全张量重力梯度仪的对比。可以看出,如果使用只能敏感一个方向的线性加速度计,则结构通常会比较复杂,或者需要3个旋转转盘来分离信号,特别是重力梯度的非对角分量,或者额外使用角加速度计来测量非对角分量以及消除动态误差。如果使用基于静电悬浮球原理的可敏感三轴方向的三轴加速度计,则不需要进行旋转,也不需要额外安装角加速度计,但需要在空间摆放6个加速度计来实现重力梯度的全张量测量,目前也仅应用于零重力的太空中。
|
|
表 1 各型全张量重力梯度仪结构对比 Tab. 1 Contrast of each gravity gradiometer for total gravity gradient tensor |
本文将可敏感三轴方向加速度的加速度计与旋转结构相结合,建立一个新的重力梯度测量结构模型,并在差分加速度测量重力梯度的已有数学研究基础之上验证其可行性。本文通过三轴加速度计与旋转相结合,使整个梯度测量系统中加速度计的数量更少,整体结构更简略,使控制精度的目标量减少,更有利于重力梯度仪的设计。
2 系统设计及数学分析图 1为本文设计的结构简图。2个三轴加速度计空间对称放置,相对位置固定,绕Z轴以角速度ω进行旋转,通过加速度计各个输出量的组合,分离出重力梯度张量的全部独立分量。
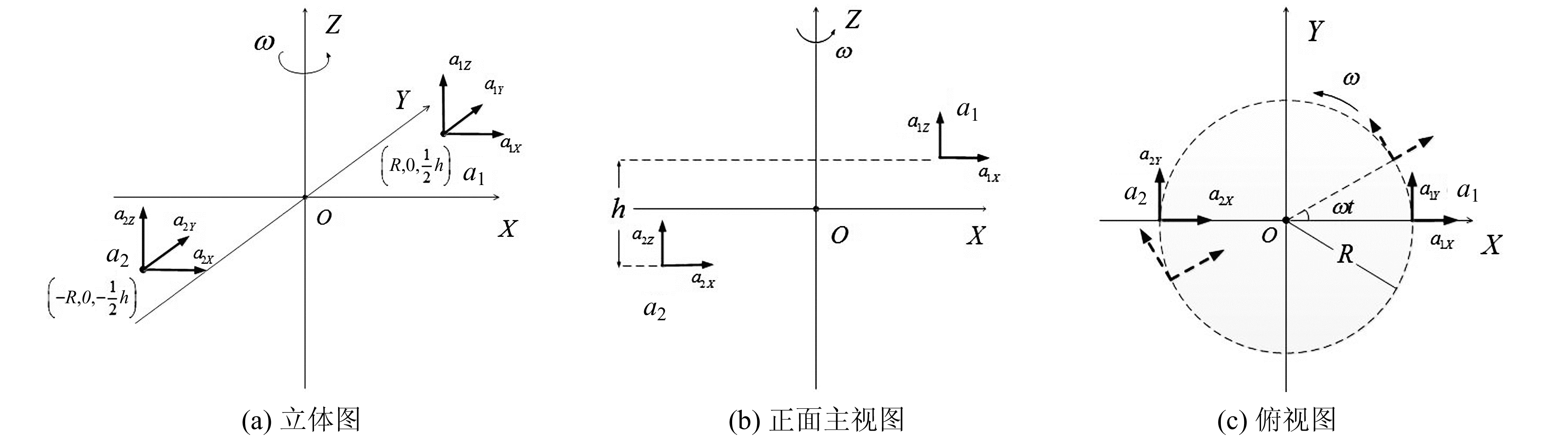
|
图 1 重力梯度测量结构简图 Fig. 1 Diagram of gravity gradient measurement |
首先确定一个加速度计坐标系XaOYa,称之为坐标系a,与图 2中的坐标系XOY在同一平面上,但坐标系a与加速度计是固连的,即XaOYa随加速度计一起旋转,而XgOYg则是惯性系,如图 2所示。
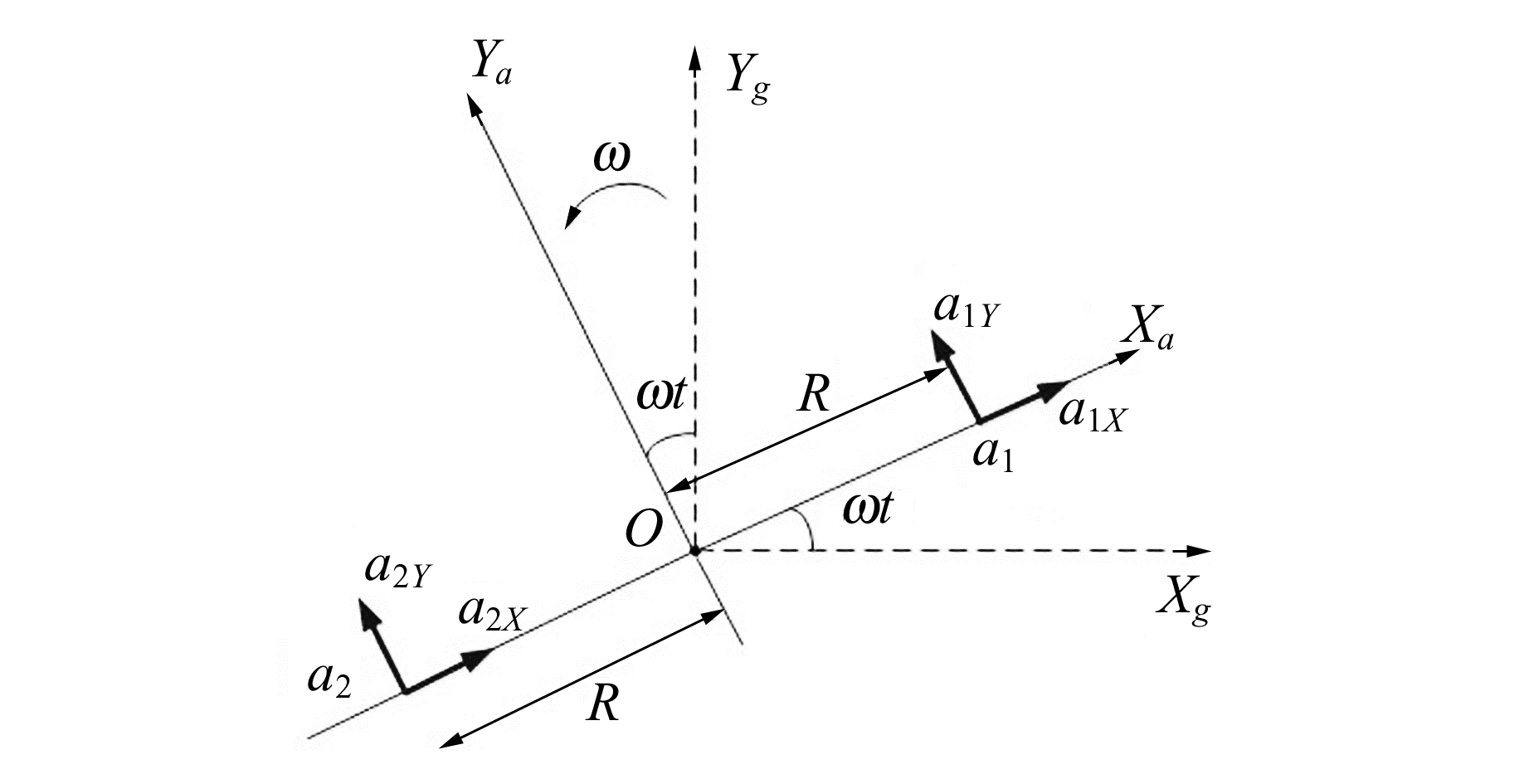
|
图 2 加速度计的坐标旋转 Fig. 2 The rotating coordinate system of accelerometer |
差分加速度获取重力梯度的公式为[8]:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{f}}_1^a - \mathit{\boldsymbol{f}}_2^a = \left[ {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^a} - \left( {{{\mathit{\boldsymbol{\dot \omega }}}_ \times }} \right) - \left( {{\mathit{\boldsymbol{\omega }}_ \times }} \right)\left( {{\mathit{\boldsymbol{\omega }}_ \times }} \right)} \right]{\mathit{\boldsymbol{\rho }}^a} = }\\ {\left[ {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^a} - \mathit{\boldsymbol{ \boldsymbol{\dot \varOmega} }} - \mathit{\boldsymbol{ \boldsymbol{\varOmega} \boldsymbol{\varOmega} }}} \right]{\mathit{\boldsymbol{\rho }}^a} = {\mathit{\boldsymbol{L}}^a}{\mathit{\boldsymbol{\rho }}^a}} \end{array} $ | (1) |
式中,f1a、f2a分别为两个加速度计在坐标系a下的测量值矩阵;Γa为加速度计在坐标系a下的重力梯度矩阵,惯性系下的重力梯度矩阵可以通过坐标变换得到;ρa为加速度计位置向量的差值矩阵,当加速度计间摆放位置相对固定时,此值恒定;La为加速度计测量值对位移直接差分后得到的梯度测量矩阵,其中还包含角速度分量ΩΩ及角加速度分量
| $ \mathit{\boldsymbol{ \boldsymbol{\varOmega} \boldsymbol{\varOmega} }} = \left[ {\begin{array}{*{20}{c}} { - \omega _y^2 - \omega _z^2}&{{\omega _x}{\omega _y}}&{{\omega _x}{\omega _z}}\\ {{\omega _x}{\omega _y}}&{ - \omega _x^2 - \omega _z^2}&{{\omega _y}{\omega _z}}\\ {{\omega _x}{\omega _z}}&{{\omega _y}{\omega _z}}&{ - \omega _x^2 - \omega _y^2} \end{array}} \right] $ | (2) |
| $ \mathit{\boldsymbol{ \boldsymbol{\dot \varOmega} }} = \left[ {\begin{array}{*{20}{c}} 0&{ - {{\dot \omega }_z}}&{{{\dot \omega }_y}}\\ {{{\dot \omega }_z}}&0&{ - {{\dot \omega }_x}}\\ { - {{\dot \omega }_y}}&{{{\dot \omega }_x}}&0 \end{array}} \right] $ | (3) |
结合图 2,加速度计a1和a2在坐标系a内的测量值矩阵为:
| $ \begin{array}{l} \mathit{\boldsymbol{f}}_1^a = {\left( {\begin{array}{*{20}{c}} {{a_{1x}},}&{{a_{1y}},}&{{a_{1z}}} \end{array}} \right)^{\rm{T}}}\\ \mathit{\boldsymbol{f}}_2^a = {\left( {\begin{array}{*{20}{c}} {{a_{2x}},}&{{a_{2y}},}&{{a_{2z}}} \end{array}} \right)^{\rm{T}}} \end{array} $ | (4) |
位移差分矩阵为:
| $ {\mathit{\boldsymbol{\rho }}^a} = \mathit{\boldsymbol{r}}_2^a - \mathit{\boldsymbol{r}}_1^a = \left[ {\begin{array}{*{20}{c}} { - R}\\ 0\\ { - h/2} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} R\\ 0\\ {h/2} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - 2R}\\ 0\\ { - h} \end{array}} \right] $ | (5) |
将式(4)、(5)代入式(1),得:
| $ \left[ {\begin{array}{*{20}{c}} {{a_{1x}} - {a_{2x}}}\\ {{a_{1y}} - {a_{2y}}}\\ {{a_{1z}} - {a_{2z}}} \end{array}} \right] = {\mathit{\boldsymbol{L}}^a}\left[ {\begin{array}{*{20}{c}} { - 2R}\\ 0\\ { - h} \end{array}} \right] $ | (6) |
式中,La为梯度测量矩阵,其中还包含角速度分量ΩΩ及角加速度分量
将式(2)、(3)代入式(6),展开得:
| $ \begin{array}{l} {a_{1x}} - {a_{2x}} = - 2RL_{11}^a - hL_{13}^a = - 2R\left( {\mathit{\Gamma }_{xx}^a + } \right.\\ \left. {\omega _y^2 + \omega _z^2} \right) - h\left( {\mathit{\Gamma }_{xz}^a - {\omega _x}{\omega _z} - {{\dot \omega }_y}} \right){a_{1y}} - {a_{2y}} = \\ - 2RL_{21}^a - hL_{23}^a = - 2R\left( {\mathit{\Gamma }_{yx}^a - {\omega _x}{\omega _y} - {{\dot \omega }_z}} \right) - \\ h\left( {\mathit{\Gamma }_{yz}^a - {\omega _y}{\omega _z} + {{\dot \omega }_x}} \right){a_{1z}} - {a_{2z}} = - 2RL_{31}^a - hL_{33}^a = \\ - 2R\left( {\mathit{\Gamma }_{zx}^a - {\omega _x}{\omega _z} + {{\dot \omega }_y}} \right) - h\left( {\mathit{\Gamma }_{zz}^a + \omega _x^2 + \omega _y^2} \right) \end{array} $ | (7) |
至此,获得了加速度计测量值与坐标系a下重力梯度的直接关系,而坐标系a下的重力梯度与惯性系下的坐标变换公式为:
| $ {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^a} = \mathit{\boldsymbol{C}}_g^a{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^g}\mathit{\boldsymbol{C}}_a^g $ | (8) |
当加速度计坐标系a绕惯性系旋转的角速度为ω时,变换公式的转置矩阵为:
| $ \begin{array}{l} \mathit{\boldsymbol{C}}_g^a = \left[ {\begin{array}{*{20}{c}} {\cos \omega t}&{\sin \omega t}&0\\ { - \sin \omega t}&{\cos \omega t}&0\\ 0&0&1 \end{array}} \right]\\ \mathit{\boldsymbol{C}}_a^g = \left[ {\begin{array}{*{20}{c}} {\cos \omega t}&{ - \sin \omega t}&0\\ {\sin \omega t}&{\cos \omega t}&0\\ 0&0&1 \end{array}} \right] \end{array} $ | (9) |
将式(9)代入式(8)并展开:
| $ \begin{array}{l} \mathit{\Gamma }_{xx}^a = \left( {1/2} \right)\left( {{\mathit{\Gamma }_{xx}} - {\mathit{\Gamma }_{yy}}} \right)\cos 2\omega t + {\mathit{\Gamma }_{yy}}\sin 2\omega t + \\ \;\;\;\;\;\;\left( {1/2} \right)\left( {{\mathit{\Gamma }_{yy}} + {\mathit{\Gamma }_{yy}}} \right)\\ \mathit{\Gamma }_{xy}^a = - \left( {1/2} \right)\left( {{\mathit{\Gamma }_{xx}} - {\mathit{\Gamma }_{yy}}} \right)\sin 2\omega t + {\mathit{\Gamma }_{xy}}\cos 2\omega t\\ \mathit{\Gamma }_{xz}^a = \cos \omega t{\mathit{\Gamma }_{xz}} + \sin \omega t{\mathit{\Gamma }_{yz}}\\ \mathit{\Gamma }_{yx}^a = - \sin \omega t{\mathit{\Gamma }_{xz}} + \cos \omega t{\mathit{\Gamma }_{yz}}\\ \mathit{\Gamma }_{zz}^a = {\mathit{\Gamma }_{zz}} \end{array} $ | (10) |
由于模型仅绕Z轴旋转,因此ωx=ωy=0,ωz恒等于ω。将式(10)代入式(7),整理得:
| $ \begin{array}{l} {a_{1x}} - {a_{2x}} = - h\sin \omega t{\mathit{\Gamma }_{yz}} - h\cos \omega t{\mathit{\Gamma }_{xz}} - \\ \;\;\;\;\;\;2R\sin 2\omega t{\mathit{\Gamma }_{xy}} - R\cos 2\omega t\left( {{\mathit{\Gamma }_{xx}} - {\mathit{\Gamma }_{yy}}} \right) - \\ \;\;\;\;\;\;R\left( {{\mathit{\Gamma }_{xx}} + {\mathit{\Gamma }_{yy}}} \right) - 2R\omega _z^2\\ {a_{1y}} - {a_{2y}} = - h\cos \omega t{\mathit{\Gamma }_{yz}} + h\sin \omega t{\mathit{\Gamma }_{xz}} - \\ \;\;\;\;\;\;2R\cos 2\omega t{\mathit{\Gamma }_{xy}} + R\sin 2\omega t\left( {{\mathit{\Gamma }_{xx}} - {\mathit{\Gamma }_{yy}}} \right) + 2R{{\dot \omega }_z}\\ {a_{1z}} - {a_{2z}} = - 2R\sin \omega t{\mathit{\Gamma }_{yz}} - 2R\cos \omega t{\mathit{\Gamma }_{xz}} - h{\mathit{\Gamma }_{zz}} \end{array} $ | (11) |
对式(11)进行分析可以发现,4个重力梯度分量Γyz、Γxz、Γxy、(Γxx-Γyy)分别附加在加速度计输出组合中的旋转角速度ω一倍频和二倍频正交信号上。通过分频,分别获取一倍频和二倍频信号,再分别通过放大解调并经由两个相差90°的检波器处理,即可获得4个重力梯度分量。此处理方法与旋转加速度计的输出信号处理方式一致[9]。而Γzz分量为Z轴方向上的加速度输出组合a1z-a2z中的常量,通过滤波即可获得该分量。至此,获得了重力梯度的全部5个独立分量。
进一步分析式(11),Γxz、Γyz以及Γzz项均含有系数h,可以理解为通过将加速度计的结构进行空间摆放形成高度差而进行分离;而对于Γxy、Γxx-Γyy,其与旋转加速度计重力梯度仪的单个转盘结构输出一致,均通过XOY平面的距离R进行分离。因此,对比旋转加速度计梯度仪的单个平面转盘结构可以发现,Γxz、Γyz、Γzz都是额外测得的量。除空间摆放加速度计带来的优势外,Γzz信号也是通过三轴加速度计的Z轴输出组合来获得的,且三轴输出都含有Γxz、Γyz分量,可以更好地对比拟合出Γxz、Γyz信号。这是本文测量结构中空间摆放加速度计及采用三轴加速度计比旋转加速度计的单个转盘结构更具优势的地方。
对比同样采用三轴加速度计及空间摆放的静电重力梯度仪,本文结构因为采用了旋转,故仅需2个三轴加速度计,而静电梯度仪则需6个,且仅能工作在室温零重力环境下;而对于超导重力梯度仪,由于此结构采用了三轴线性加速度计,而不需要使用角加速度计,可以避免更多复杂的结构以及由此带来的误差。
3 结语本文以三轴加速度计为核心,与旋转结构相结合,提出一种全张量重力梯度测量系统。利用三轴加速度计的合理空间摆放及旋转结构,通过加速度计输出的组合成功分离出了重力梯度的全部独立分量,从数学上验证了该系统的理论可行性以及结构上的优越性。
重力梯度仪的研制是一项极其精密、细致而且长期的工程,从结构模型的提出到应用有非常长的距离要走。本文模型不仅涉及到单个加速度计的精度,还涉及到旋转系统的稳定性问题,故高精度的三轴加速度计及高稳定性的旋转结构对该系统的精度和实际应用至为关键。虽然该系统暂时处于理论研究阶段,但随着高精度高稳定性加速度计的发展,这一系统将会逐步实现。
| [1] |
Moody M V, Paik H J, Canavan E R. Three-Axis Superconducting Gravity Gradiometer for Sensitive Gravity Experiments[J]. Review of Scientific Instruments, 2002, 73(11): 3 957-3 974 DOI:10.1063/1.1511798
(  0) 0) |
| [2] |
Drinkwater M R, Floberghagen R, Haagmans R, et al. GOCE: ESA's First Earth Explorer Core Mission[J]. 2003, 108(1): 419-432
(  0) 0) |
| [3] |
Lee J B. FALCON Gravity Gradiometer Technology[J]. Exploration Geophysics, 2001, 32(4): 247-250 DOI:10.1071/EG01247
(  0) 0) |
| [4] |
吴琼, 滕云田, 张兵, 等. 世界重力梯度仪的研究现状[J]. 物探与化探, 2013, 37(5): 761-768 (Wu Qiong, Teng Yuntian, Zhang Bing, et al. The Research Situation of the Gradiometer in the World[J]. Geophysical & Geochemical Exploration, 2013, 37(5): 761-768 DOI:10.11720/j.issn.1000-8918.2013.5.01)
(  0) 0) |
| [5] |
Moody M V, Paik H J, Canavan E R. Principle and Performance of a Superconducting Angular Accelerometer[J]. Review of Scientific Instruments, 2003, 74(3): 1 310-1 318 DOI:10.1063/1.1539894
(  0) 0) |
| [6] |
Moody M V, Paik H J. A Superconducting Gravity Gradiometer for Inertial Navigation[J]. IEEE Position Location and Navigation Symposium, 2004, 26(4): 775-781
(  0) 0) |
| [7] |
祝竺, 周泽兵. 静电重力梯度仪及其在卫星重力梯度测量中的应用[C]. 小卫星技术交流会, 西安, 2011 (Zhu Zhu, Zhou Zebing. Electrostatic Gravity Gradiometer and Its Application to Satellite Gravity Gradiometry[C]. Small Satellite Technology Meeting, Xi'an, 2011)
(  0) 0) |
| [8] |
刘凤鸣, 赵琳, 王建敏. 基于加速度计重力梯度仪分析与设计[J]. 地球物理学进展, 2009, 24(6): 2 058-2 062 (Liu Fengming, Zhao Lin, Wang Jianmin. The Design and Analysis for the Accelerometer-Based Gravity Gradiometer[J]. Progress in Geophysics, 2009, 24(6): 2 058-2 062)
(  0) 0) |
| [9] |
罗嗣成. 旋转加速度计重力梯度仪[D]. 武汉: 华中科技大学, 2007 (Luo Sicheng. Rotating Accelerometer Gravity Gradiometer[D]. Wuhan: Huazhong University of Science and Technology, 2007) http://cdmd.cnki.com.cn/Article/CDMD-10487-2009036749.htm
(  0) 0) |
2. University of the Chinese Academy of Science, A19 Yuquan Road, Beijing 100049, China;
3. Institute of Geodesy and Geophysics, CAS, 340 Xudong Street, Wuhan 430077, China
 2018, Vol. 38
2018, Vol. 38

