2. 郑州测绘学校,郑州市大学南路1号,450000
《国家一、二等水准测量规范》规定,一等水准测量路线上的每个水准点均应测定重力;高程大于4 000 m或水准点间平均高差为150~250 m的二等水准路线上,每个水准点也应测定重力;高差大于250 m的一、二等水准测段中,地面倾斜变化处应加测重力,以便在水准计算时进行高差改正[1]。当前的高精度水准测量中,考虑到费用和工期等要求,对重力异常的改正往往采用布格异常内插的方法进行。鉴于此,本文采用两种方式对高精度水准测量进行重力异常改正:1)将水准点标绘在不小于1 :1 000 000布格异常图上,内插求出该测段布格异常(g-γ)布,取至10 mGal,利用公式求出相应的高差改正值[2];2)在水准点上进行重力测量,根据实测重力值计算测段的空间重力异常(g-γ)空,利用相同的公式求出测段的高差改正值。分别得到重力空间异常值后,计算水准点高程异常改正值,并对两种高差改正结果进行比较,得到标绘布格异常的高差中误差,分析该方法对高程改正结果的精度影响。
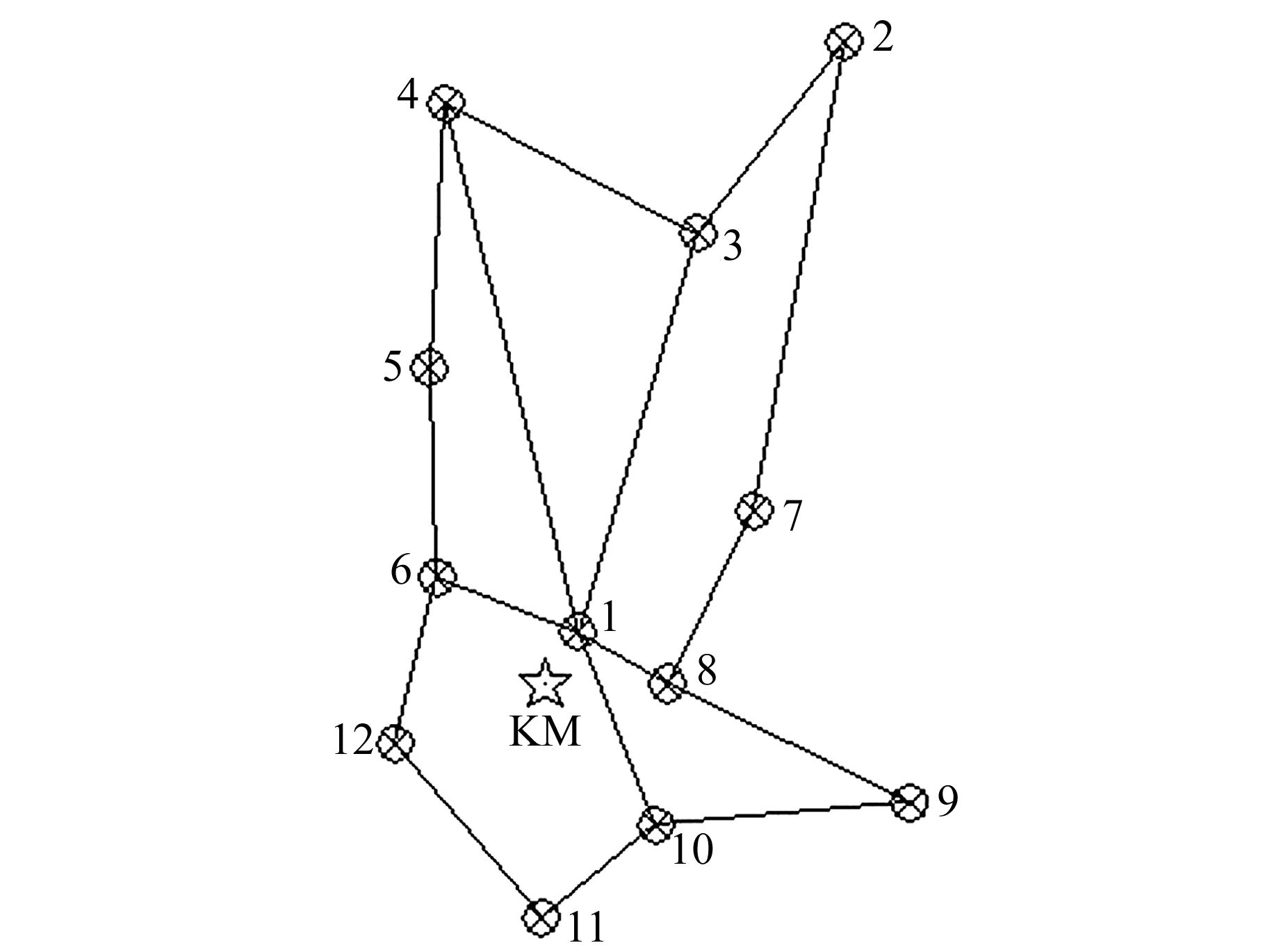
1 测量概况选取昆明市周边地区12个一等水准点,东西跨度约60 km,南北跨度约80 km。一等水准测量采用Dini03精密水准仪进行,高程范围1 726~2 359 m。对该一等水准点采用3台CG-5型重力仪同时进行重力测量,联测方式采用对称观测,即A→B→C→D…D→C→B→A,且A→…→A的闭合时间控制在24 h内,精度可以达到进行重力异常改正的要求[3-5]。与绝对重力点进行联测,可获得相应水准点的绝对重力值。点位分布如图 1所示。
|
图 1 测点分布 Fig. 1 Distribution of measuring points |
某一测段高差的改正数λ为:
| $ \lambda = {\left( {g-\gamma } \right)_{\rm{空}}}\cdot{H_m}/{\gamma _m} $ | (1) |
式中,Hm为2水准点概略高程平均值,单位m;γm为2水准点正常重力平均值,单位mGal:
| $ {\gamma _{\rm{空}}} = ({\gamma _i} + {\gamma _{i + 1}})/2-0.154\;3{H_m} $ | (2) |
| $ \begin{array}{l} \gamma = 978\;032(1 + 0.005\;302\;4{\rm{si}}{{\rm{n}}^2}\varphi-{\rm{ }}\\ \;\;\;\;\;\;\;\;0.000\;005\;8{\rm{si}}{{\rm{n}}^2}2\varphi ) \end{array} $ | (3) |
式中,γ值取至0.01 mGal,φ为水准点纬度。
水准点的布格异常(g-γ)布从相应的数据库中检索,取至0.1 mGal;水准点的空间重力异常(g-γ)空由式(4)计算:
| $ {\left( {g-\gamma } \right)_{\rm{空}}} = {\left( {g-\gamma } \right)_{\rm{布}}} + 0.111\;9H $ | (4) |
式中,(g-γ)空为2水准点的空间重力异常平均值,H为水准点概略高程[6]。
将水准点标绘在1 :1 000 000布格异常图上,内插得各水准点的布格异常(g-γ)布,取至10 mGal。由式(1)~(4)计算得到(g-γ)空1和高差改正数λ1,结果见表 1。
|
|
表 1 布格改正和实测改正结果 Tab. 1 Results of Bouguer correction and measurement correction |
2水准点之间的空间重力异常平均值(g-γ)空与布格异常的计算方式不同,由实际测量的重力值计算获得。水准点的重力异常(g-γ)空2和高差改正数λ2见表 1。
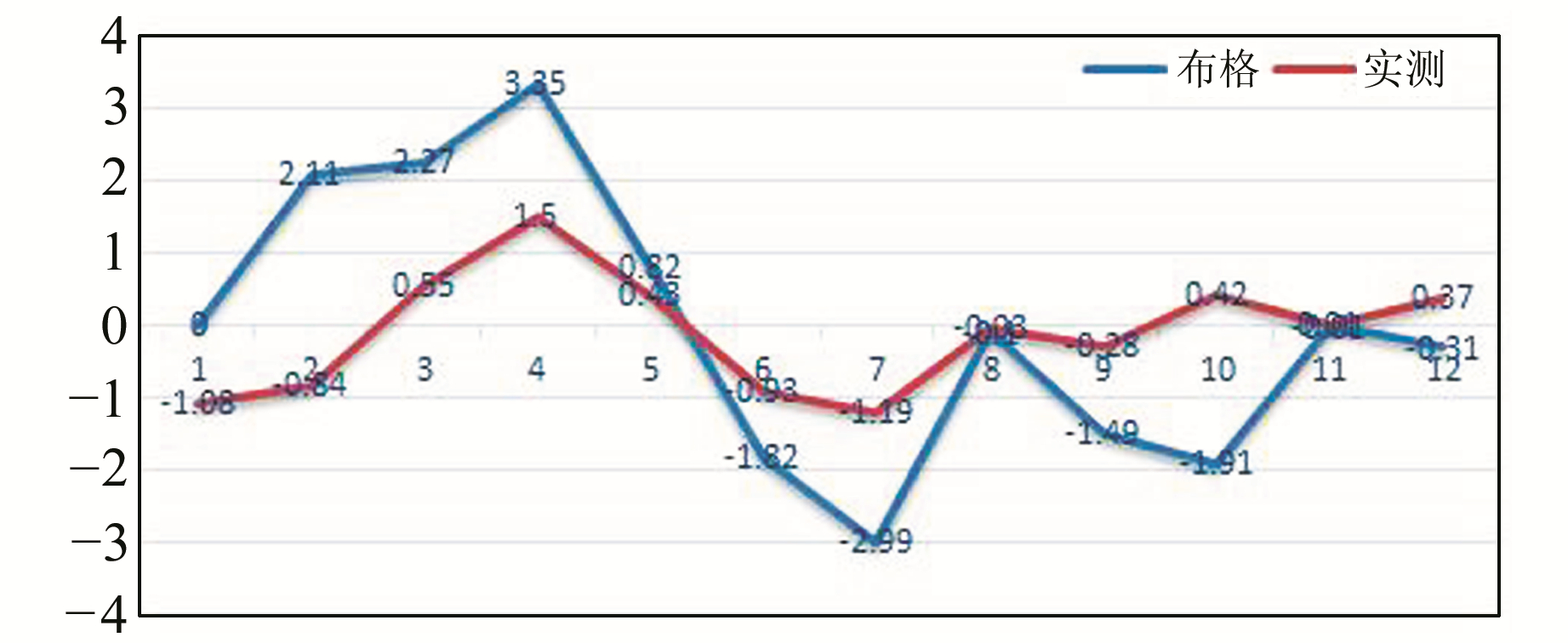
3 比较分析以实测重力计算得到的重力异常高程改正结果为基准,得到布格异常重力改正和实测重力改正的高程差值,如表 2所示,差值分布如图 2所示。可以看出,差值绝对值的平均值为1.25 mm,2号点的差值最大,为2.95 mm,高差差值中误差为2.32 mm。
|
|
表 2 结果比较 Tab. 2 Results of comparison |
|
图 2 差值分布 Fig. 2 The difference distribution |
采用图上量取内插计算得到的重力布格异常值,未能充分考虑实地情况对重力值的影响,改正后得到的结果可能存在很大的误差,如本文计算得到的某些点在高程改正中存在约3 mm的误差。这种情况下,是不能作为高精度水准测量高程改正使用的。在进行一、二等及精度较高的水准测量时,为得到准确的水准测量结果,应该使用实测重力值进行水准点的重力异常改正。
| [1] |
国家质量技术监督局. GB/T 12897-2006国家一、二等水准测量规范[S]. 北京: 中国标准出版社, 2006 (State Bureau of Quality Technical Supervision. GB/T 12897-2006 Specifications for the First and Second Order Leveling[S]. Beijing: China Standards Press, 2006)
(  0) 0) |
| [2] |
国家质量技术监督局. GB/T 12898-2009国家三、四等水准测量规范[S]. 北京: 中国标准出版社, 2009 (State Bureau of Quality Technical Supervision. GB/T 12898-2009 Specifications for the Third and Fourth Order Leveling[S]. Beijing: China Standards Press, 2009)
(  0) 0) |
| [3] |
谢慧洪, 叶勤. 大城市精密水准网复测中新技术、新工艺的应用——以上海市为例[J]. 测绘通报, 2016(1): 68-71 (Xie Huihong, Ye Qin. Application of New Technology in Repetition of Megacity Precise Leveling Network—A Case Study of Shanghai[J]. Bulletin of Surveying and Mapping, 2016(1): 68-71)
(  0) 0) |
| [4] |
郝林, 李建成, 褚永海. 1985国家高程基准与全球高程基准之间的垂线偏差[J]. 测绘学报, 2016, 45(7): 768-774 (Hao Lin, Li Jiancheng, Chu Yonghai. The Vertical Shift between 1985 National Height Datum and Global Vertical Datum[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(7): 768-774 DOI:10.11947/j.AGCS.2016.20160029)
(  0) 0) |
| [5] |
邢乐林, 李辉, 夏正超, 等. CG-5重力仪零漂特性研究[J]. 地震学报, 2010, 32(3): 369-373 (Xing Lelin, Li Hui, Xia Zhengchao, et al. Study on Zero Drift Characteristics of CG-5 Gravimeter[J]. Acta Seismologica Sinica, 2010, 32(3): 369-373)
(  0) 0) |
| [6] |
邹俊平. 2011年上海市精密水准网复测数据处理与分析[J]. 城市勘测, 2012(5): 94-97 (Zou Junping. Data Processing and Analysis of Shanghai Precise Leveling Network in 2011[J]. Urban Geotechnical Investigation & Surveying, 2012(5): 94-97)
(  0) 0) |
2. Zhengzhou School for Surveying and Mapping, 1 South-Daxue Road, Zhengzhou 450000, China
 2018, Vol. 38
2018, Vol. 38

