2. 西安测绘研究所,西安市雁塔路中段1号,710054;
3. 地理信息工程国家重点实验室,西安市雁塔路中段1号,710054;
4. 城市空间信息工程北京市重点实验室,北京市羊坊店路15号,100038
卫星重力测量技术[1]日趋成熟,如CHAMP、GRACE以及GOCE卫星[2-5]。卫星重力代表的是地球重力场的中长波部分[6],即地球深部信息。进行重力场与其场源深度关系的研究,能更好地推进卫星重力数据的实际应用。
通过研究小波基和小波阶数,可以对重力场进行小波多尺度分析[7-11],再结合功率谱埋深估计技术,就能对重力场与场源深度的关系作出推断。本文使用恰当的小波基和小波阶数分解卫星重力场,并根据其结果计算南海北部陆缘地区的莫霍面深度,结果表现良好。
1 重力场场源模型设置卫星重力是不同深度物质引起的叠加重力场。因此,在设置场源时,模型应设置为多层,且场源必须包括地球表面和深部物质。本文以两层分布的5个质量块体来模拟地球局部重力场,也符合多尺度重力场的设定。
1.1 模型重力场原理采用常用的直立六面体组合作为重力场场源模型,其计算公式为[12]:
| $ \begin{array}{l} G =- P\sum\limits_{q = 1}^m {\sum\limits_{s = 1}^n {\sum\limits_{L = 1}^t {\sum\limits_{i = 1}^2 {\sum\limits_{j = 1}^2 {\sum\limits_{k = 1}^2 {{\mu _{ijk}}[{x_i}{\rm{ln}}({y_j} + {r_{ijk}}) + {\rm{ }}} } } } } } \\ \;\;\;\;\;\;\;\;\;\;\;\; {y_j}{\rm{ln}}({x_i} + {r_{ijk}})-{z_k}{\rm{arctan}}(\frac{{{x_i}{y_j}}}{{{z_k}{r_{ijk}}}})] \end{array} $ | (1) |
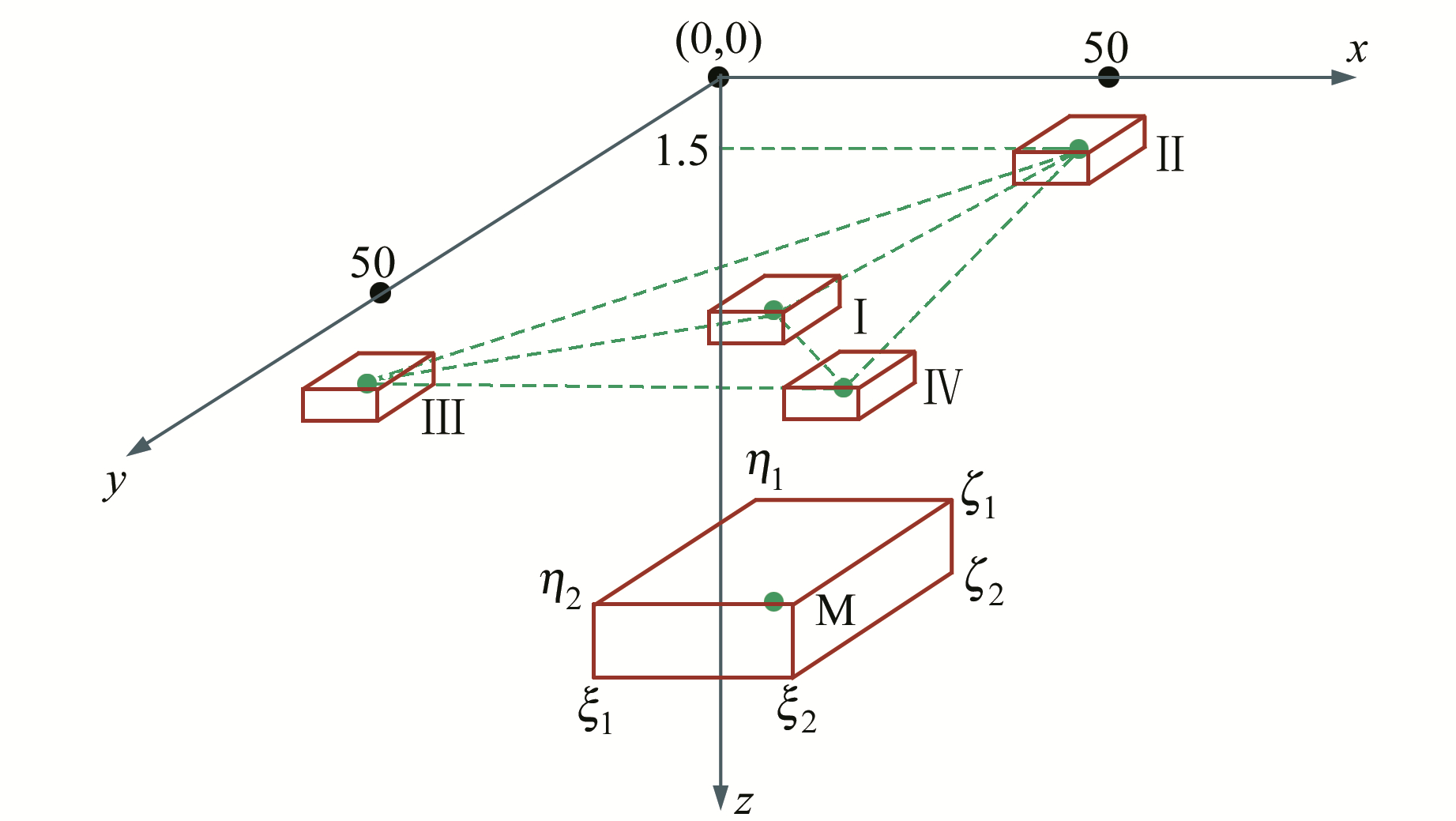
式中,P为牛顿万有引力常数;m、n为观测面横纵向点数;t为直立六面体个数;ξ、η、ζ为直立六面体的8个角坐标(如图 1);μijk=(-1)i+j+k, i, j, k=1, 2;
|
图 1 模型示意图 Fig. 1 The sketch figure of model |
本文组合模型由1个大长方体和4个小长方体构成(图 1),区域重力异常由埋藏较深的大长方体产生,局域重力异常由埋藏较浅的小长方体产生。该组合具有复杂的排列分布(左右对称、中心不对称),且有大异常、小异常,以此模拟真实重力场的复杂程度。组合模型参数见表 1,M为大长方体(平均埋深30 km);Ⅰ、Ⅱ、Ⅲ、Ⅳ为小长方体(平均埋深1.5 km);剩余密度为0.2 g/cm3。
|
|
表 1 组合模型参数 Tab. 1 The parameter of the combination model |
根据表 1中的参数,按照式(1)计算模型重力场(图 2),作为研究输入数据。

|
图 2 模型重力异常 Fig. 2 The map of model gravity anomaly |
重力场是叠加场,为研究不同规模、形态和埋深的场源物质,必须对重力异常进行分离[13-15],主要方法有滑动平均算法、导数计算法、小波算法等。小波多尺度分析是近年来研究热点,但小波基和分解阶数的选择仍然是一个难点[16]。
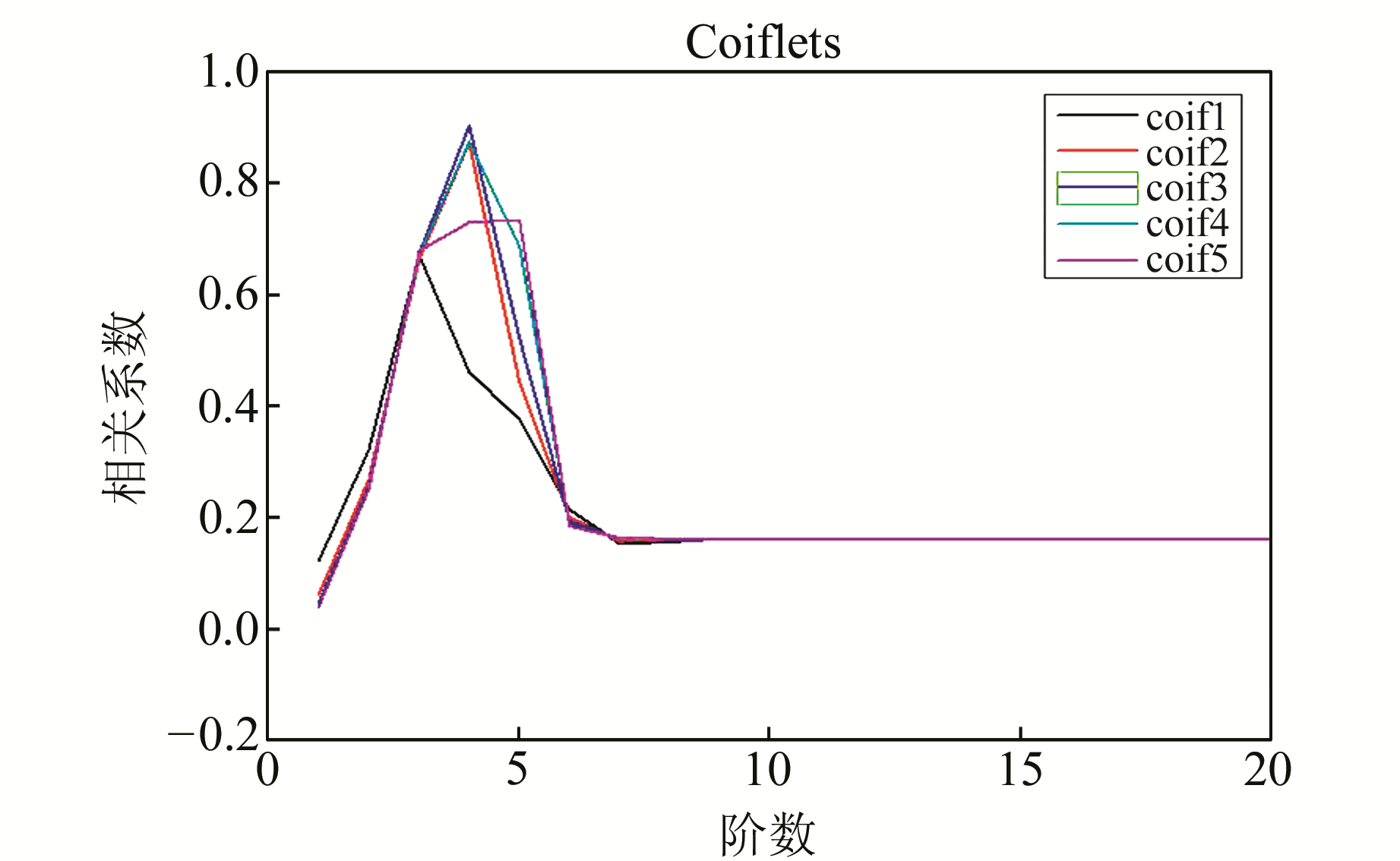
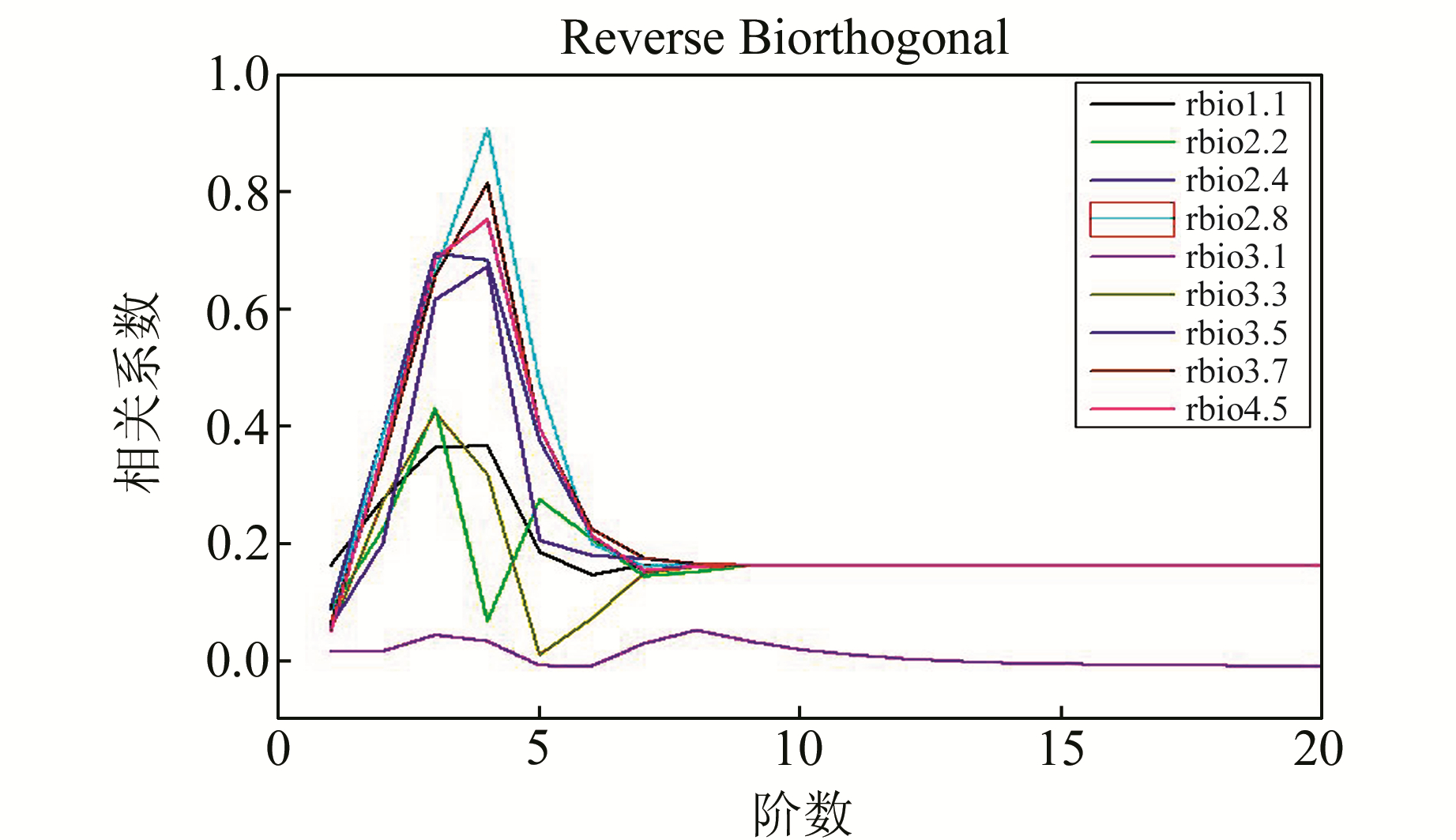
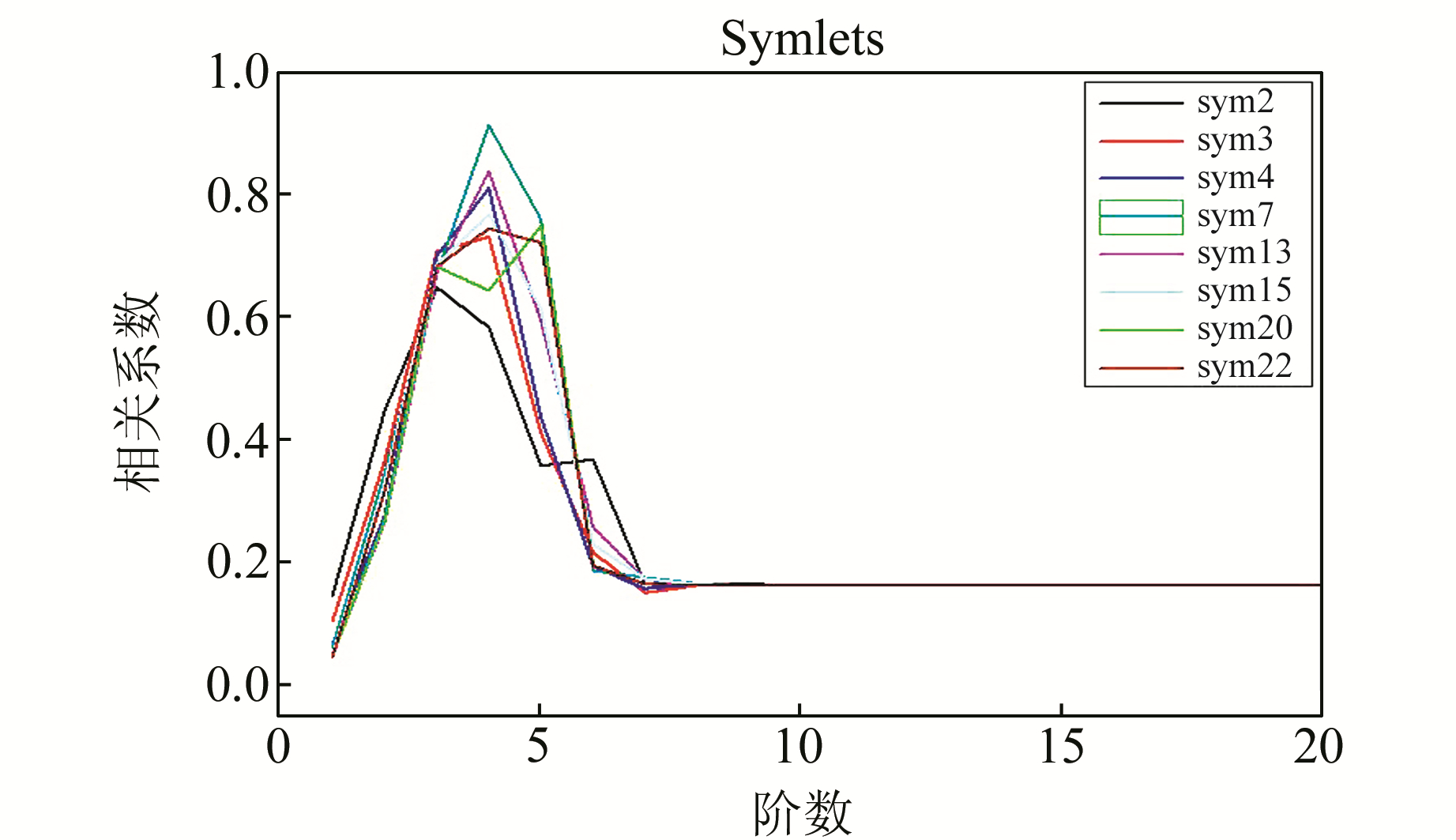
本文利用Biorthogonal、Coiflets、Daubechies、Discrete Meyer、Reverse Biorthogonal、Symlets 6种小波基对总场重力异常(图 2(a))进行分解,阶数选取为1~20阶,并求取分解结果的高频场与局域重力异常的相关系数。图 3~8只列出了差异较大的结果。

|
图 3 Biorthogonal小波基系相关分析图 Fig. 3 The correlation figure of Biorthogonal wavelets |
|
图 4 Coiflets小波基系相关分析图 Fig. 4 The correlation figure of Coiflets wavelets |

|
图 5 Daubechies小波基系相关分析图 Fig. 5 The correlation figure of Daubechies wavelets |

|
图 6 Discrete Meyer小波基系相关分析图 Fig. 6 The correlation figure of Discrete Meyer wavelets |
|
图 7 Reverse Biorthogonal小波基系相关分析图 Fig. 7 The correlation figure of Reverse Biorthogonal wavelets |
|
图 8 Symlets小波基系相关分析图 Fig. 8 The correlation figure of Symlets wavelets |
在每种小波基系中选取相关系数最接近1的小波基进行对比分析(图 9)。由图 9可知,小波分解阶数为4时,所有小波基的计算结果最接近模型局域重力异常,且其中coif3、db19、rbio2.8、sym7的计算结果极为相近。通过实际测试,最终选定db19为最优小波基,最优小波分解阶数为4。
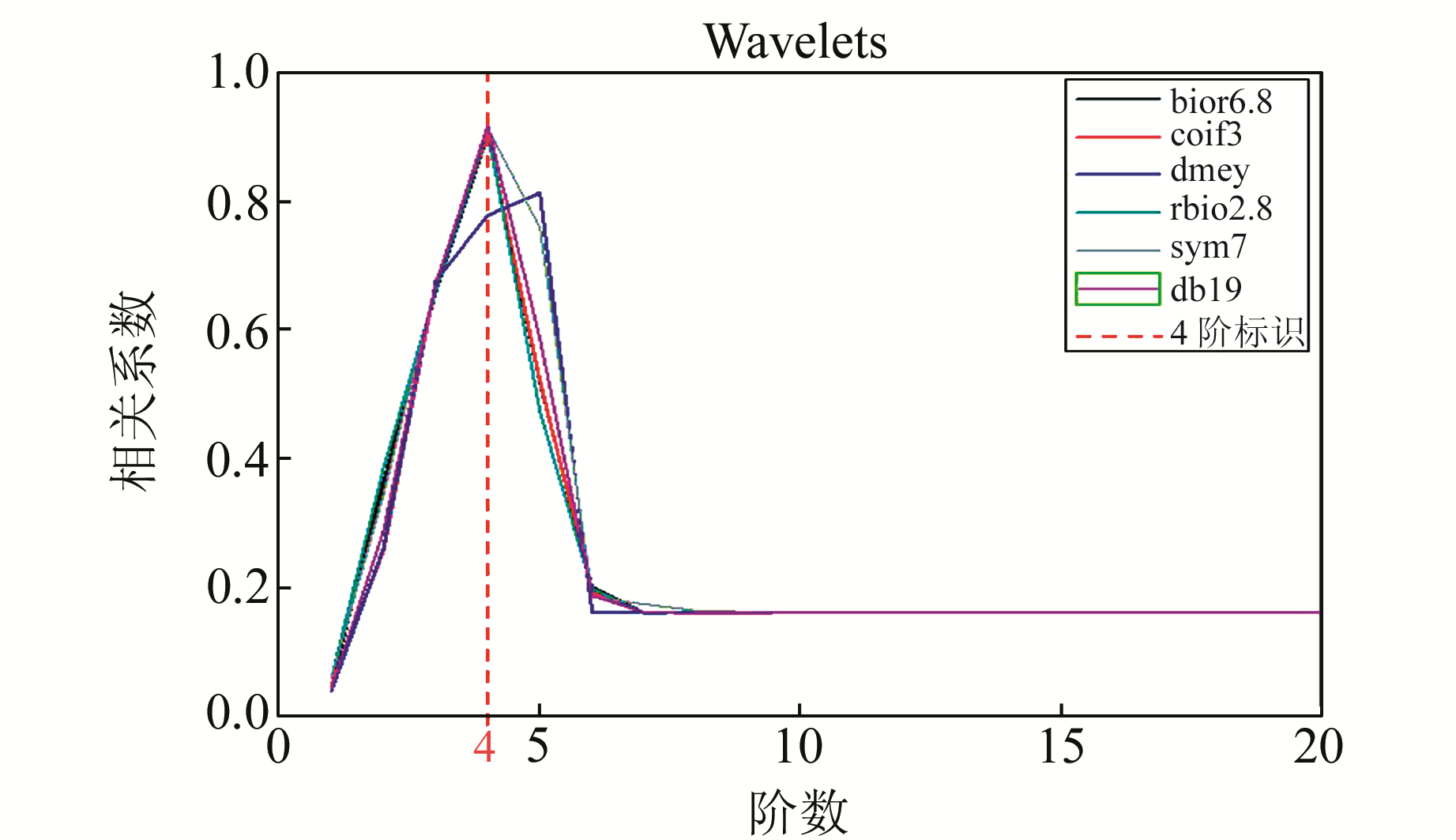
|
图 9 最优小波基系相关分析图 Fig. 9 The correlation figure of optimization wavelets |
使用最优小波分解参数对总场重力异常进行处理,其结果的高频和低频部分对应于局域、区域模型重力异常,幅值大小和异常形态与输入重力场极为接近(图 10、11)。
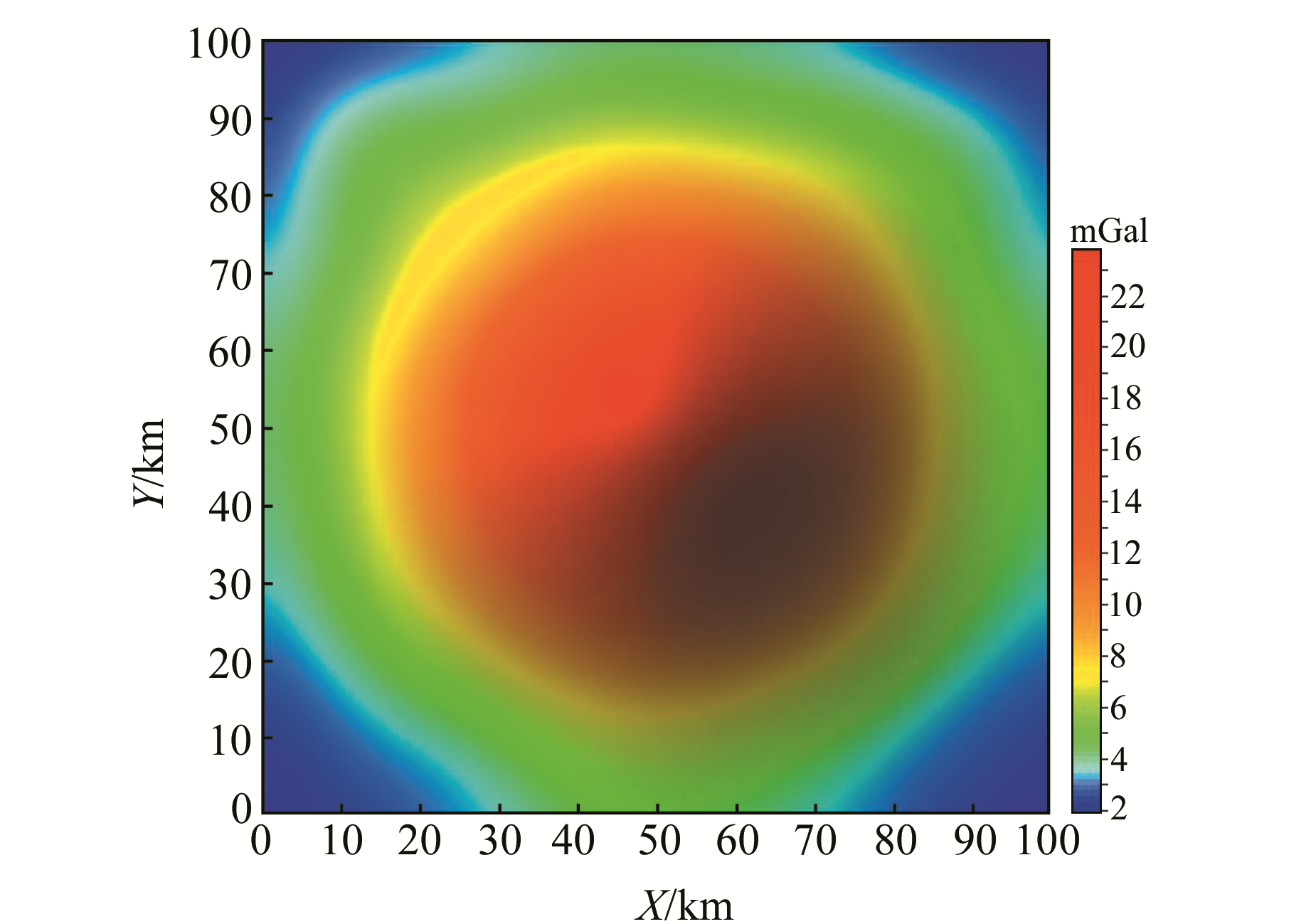
|
图 10 小波分解低频结果图 Fig. 10 The map of wavelet low frequency |

|
图 11 小波分解高频结果图 Fig. 11 The map of wavelet high frequency |
不同阶的小波低频重力场对应不同的地质体深度信息。根据位场频谱理论[17-19],其场源埋深为:
| $ {h_j} = \frac{1}{{4\pi }}\frac{{\Delta {\rm{ln}}P_k^j}}{{\Delta {k_j}}}\;\;\;\;\;\;j = 1, 2, \ldots, J $ | (2) |
式中,ΔlnPkj与Δkj是lnPkj与kj的变化率,j=1, 2, …, J为分解阶数,hj为埋深,kj为波数,Pkj为功率谱。
根据功率谱波数图(图 12、13),由式(2)计算低频和高频场的平均埋深分别为29.4 km、1.9 km,与预设模型的平均埋深基本一致。
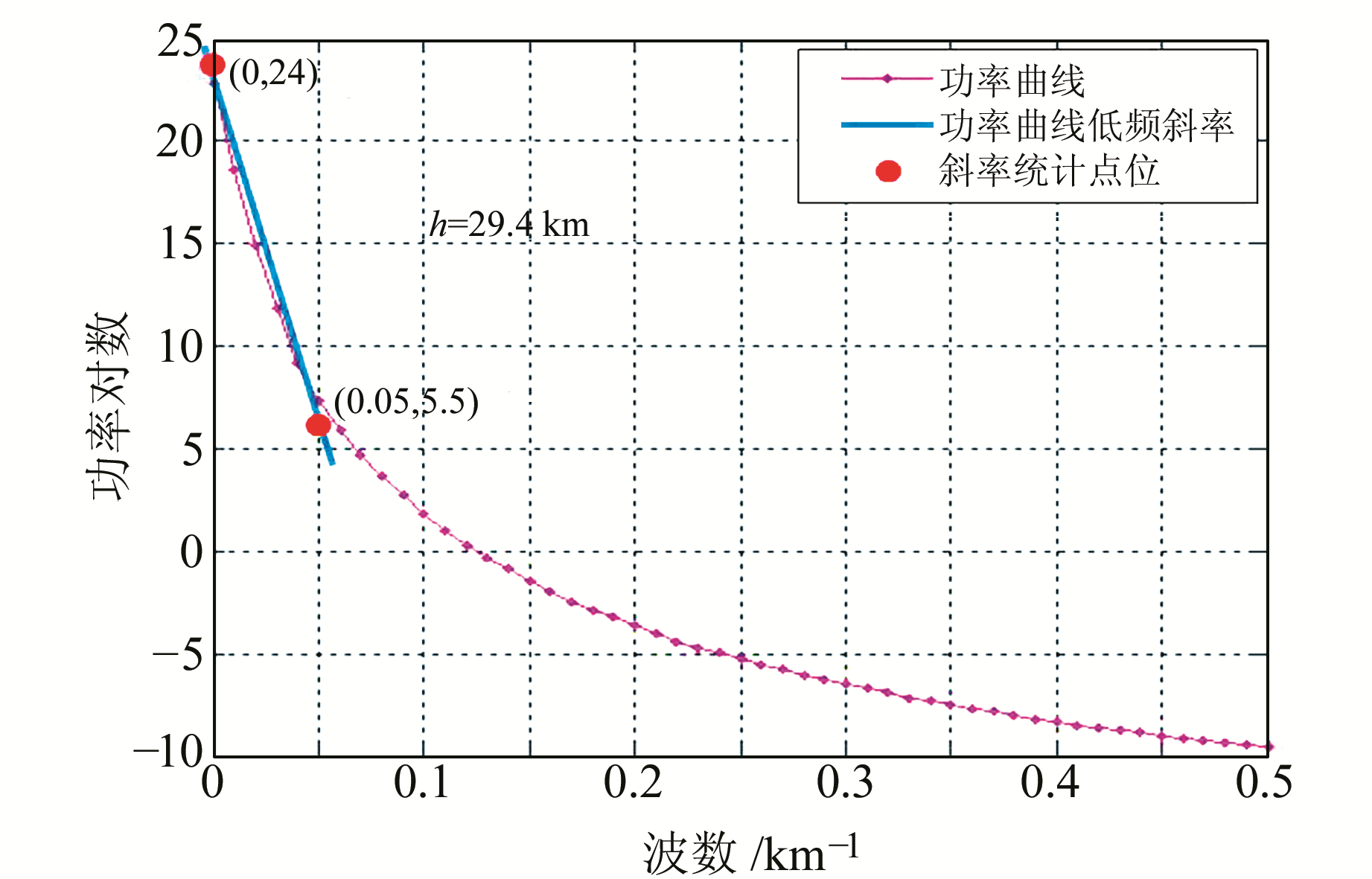
|
图 12 低频功率谱波数图 Fig. 12 The power spectrum figure of low frequency |

|
图 13 高频功率谱波数图 Fig. 13 The power spectrum figure of high frequency |
本文研究区域为南海北部陆缘地区[20],范围115°~120°E、18°~23°N。重力数据为分辨率1′×1′的布格重力异常(图 14),来自斯克里普斯海洋协会和美国国家海洋与大气局卫星测高实验室共同维护的全球卫星重力异常数据库。
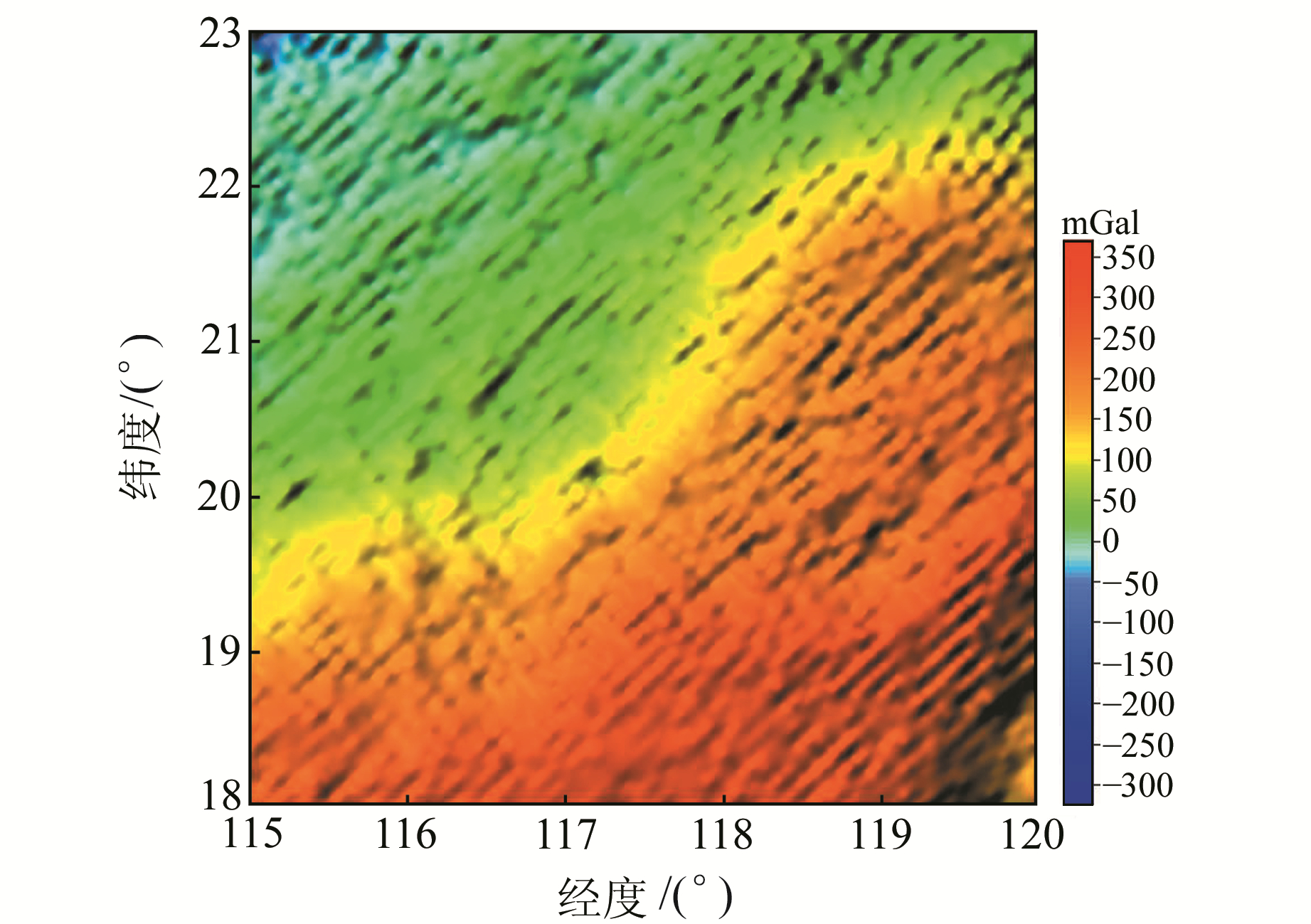
|
图 14 研究区布格重力异常图 Fig. 14 Bouguer gravity anomaly in study area |
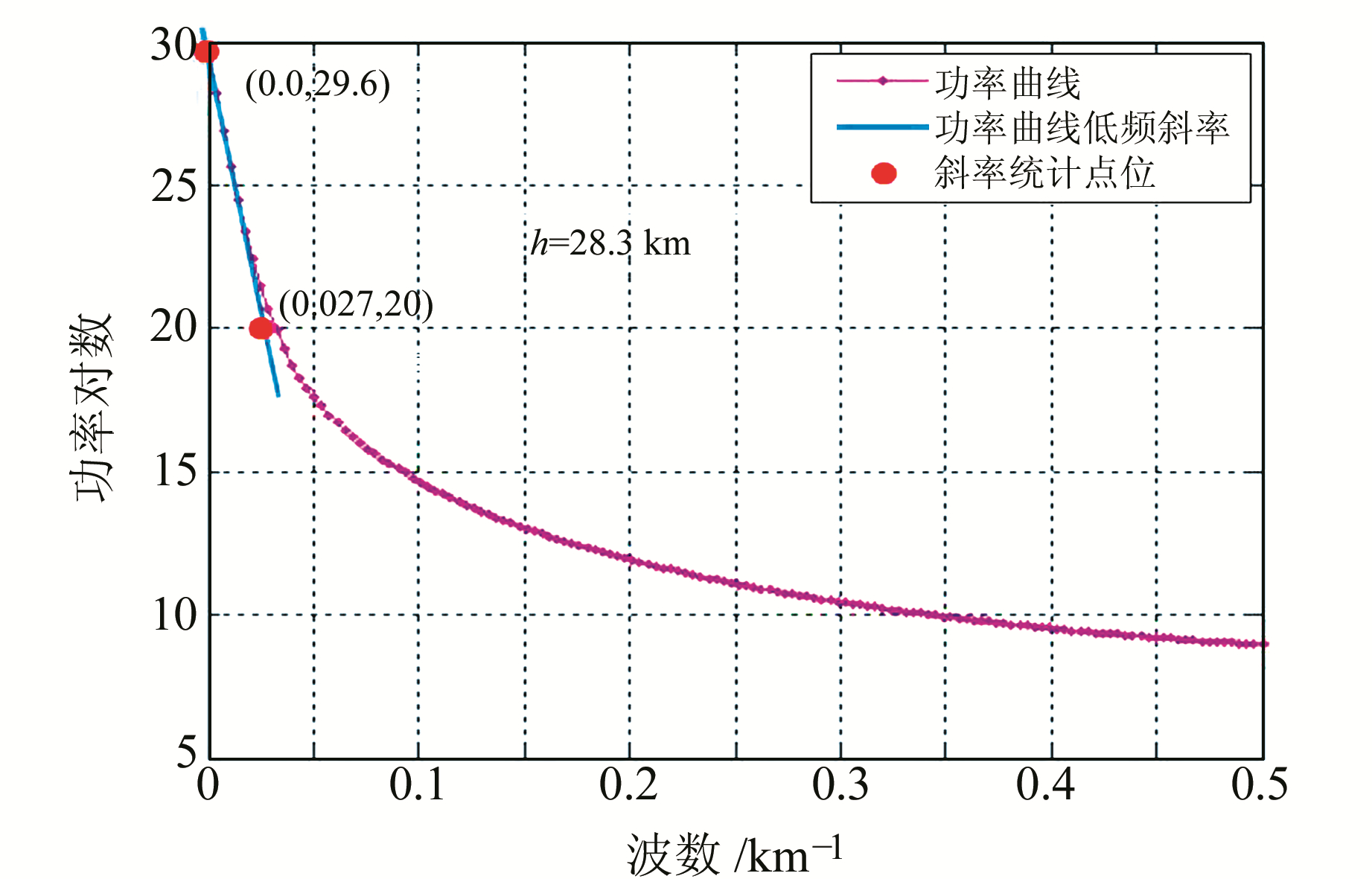
使用最优小波分解参数(小波基db19,分解阶数4)计算南海北部陆缘地区布格重力异常的4阶小波逼近(图 15)。布格重力异常一般表征了莫霍面的起伏形态,其小波分解的低频场(即区域布格重力异常)与莫霍面起伏更为吻合[20]。根据功率谱波数图(图 16),南海北部陆缘地区莫霍面深度约为28.3 km,这与北部陆架地区莫霍面深度在26~30 km之间的结论[20]相吻合。

|
图 15 研究区4阶小波逼近图 Fig. 15 4 orders wavelet approximations in study area |
|
图 16 研究区4阶小波逼近功率谱波数图 Fig. 16 The power spectrum figure of 4 orders wavelet approximations in study area |
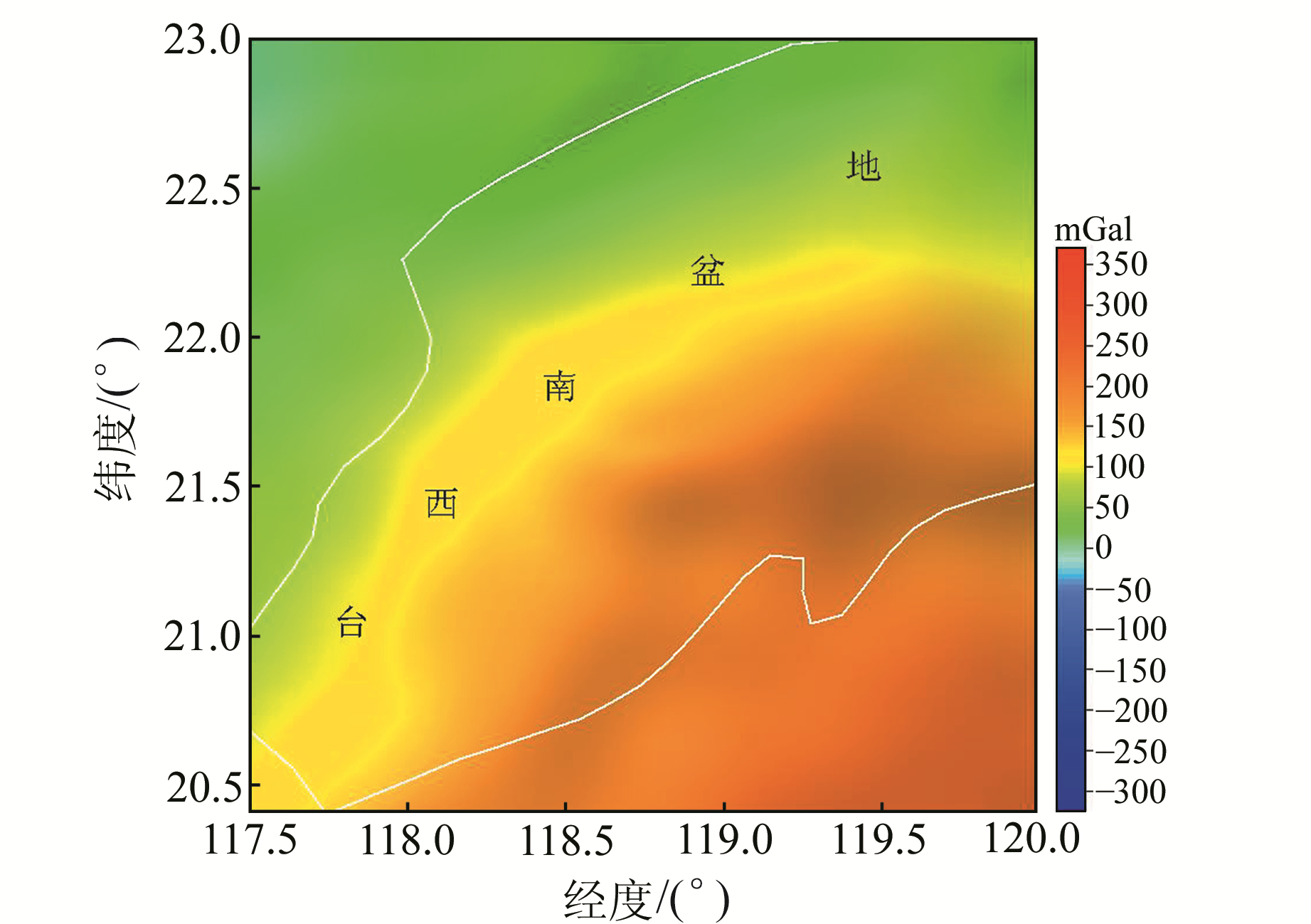
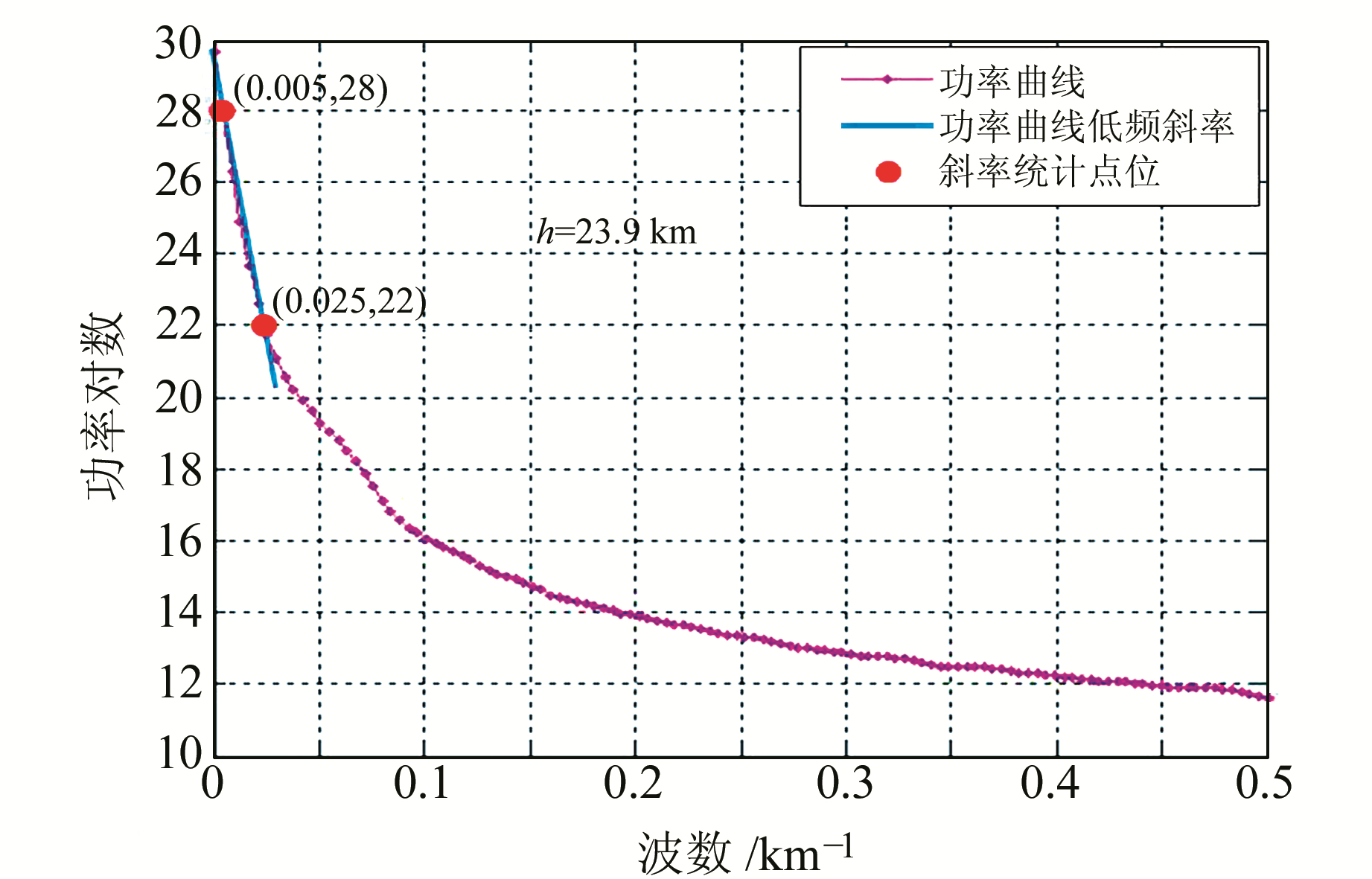
为进一步研究功率谱深度估计算法的准确性,从南海北部陆缘地区裁剪出珠江口盆地和台西南盆地的4阶小波逼近布格重力异常(图 17、18),分别进行深度计算,结果为23.9 km、20.8 km(图 19、20)。

|
图 17 珠江口4阶小波逼近图 Fig. 17 4 orders wavelet approximations in Zhujiangkou |
|
图 18 台西南4阶小波逼近图 Fig. 18 4 orders wavelet approximations in Taixinan |
|
图 19 珠江口4阶小波逼近功率谱波数图 Fig. 19 The power spectrum figure of 4 orders wavelet approximations in Zhujiangkou |

|
图 20 台西南4阶小波逼近功率谱波数图 Fig. 20 The power spectrum figure of 4 orders wavelet approximations in Taixinan |
将以上深度计算结果与收集的资料进行对比(表 2),功率谱波数图(图 16、19、20)得到的深度与文献[20]结论一致,表明功率谱的深度计算结果可以表征区域莫霍面平均深度。
|
|
表 2 莫霍面深度结果 Tab. 2 The depth of the Moho |
1) 布格重力异常区域幅值趋势与莫霍面深度分布相关,使用小波多尺度分解提取布格重力异常区域信息很有必要。
2) 根据功率谱波数图估算出的深度具有统计意义,代表区域平均深度。
3) 深度估算结果表明,研究区布格重力异常的区域背景主要是由莫霍面产生的。
| [1] |
曾华霖. 重力场与重力勘探[M]. 北京: 地质出版社, 2005 (Zeng Hualin. Gravity Field and Gravity Exploration[M]. Beijing: Geological Publishing House, 2005)
(  0) 0) |
| [2] |
罗志才, 吴云龙, 钟波, 等. GOCE卫星重力梯度测量数据的预处理[J]. 武汉大学学报:信息科学版, 2009, 34(10): 1 163-1 167 (Luo Zhicai, Wu Yunlong, Zhong Bo, et al. Preprocessing of the GOCE Satelite Gravity Gradiometry Data[J]. Geomatics and Information Science of Wuhan University, 2009, 34(10): 1 163-1 167)
(  0) 0) |
| [3] |
祝竺, 周泽兵. 用于卫星重力梯度测量的加速度计性能参数分析[J]. 大地测量与地球动力学, 2012, 32(5): 148-153 (Zhu Zhu, Zhou Zebing. Analysis of Accelerometer Performance Parameters for Satellite Gravity Gradiometry[J]. Journal of Geodesy and Geodynamics, 2012, 32(5): 148-153)
(  0) 0) |
| [4] |
詹金刚, 王勇, 郝晓光. GRACE时变重力位系数误差的改进去相关算法[J]. 测绘学报, 2011, 40(4): 442-446 (Zhan Jingang, Wang Yong, Hao Xiaoguang. Improved Method for Removal of Correlated Errors in GRACE Data[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 442-446)
(  0) 0) |
| [5] |
周新, 邢乐林, 邹正波, 等. GRACE时变重力场的高斯平滑研究[J]. 大地测量与地球动力学, 2008, 28(3): 41-45 (Zhou Xin, Xing Lelin, Zou Zhengbo, et al. Study on Gaussian Smoothing of GRACE Temporal Gravity Variation[J]. Journal of Geodesy and Geodynamics, 2008, 28(3): 41-45)
(  0) 0) |
| [6] |
王留朋, 郭燕平, 冯炜. GOCE重力卫星在军事上的应用前景分析[J]. 地理空间信息, 2011, 9(1): 11-15 (Wang Liupeng, Guo Yanping, Feng Wei. GOCE Satellite Gravity in Military Application Prospect Analysis[J]. Geospatial Information, 2011, 9(1): 11-15)
(  0) 0) |
| [7] |
陈国雄, 孙劲松, 刘天佑. GRACE卫星时变重力场的小波多尺度分解——以2008年汶川Ms8.0大地震为例[J]. 武汉大学学报:信息科学版, 2012, 37(6): 679-682 (Chen Guoxiong, Sun Jinsong, Liu Tianyou. Wavelet Multi-Scal Decomposition of Time Variable Gravity Field Detected by GRACE Satellite: A Case from Wenchuan Ms8.0 Earthquake, 2008[J]. Geomatics and Information Science of Wuhan University, 2012, 37(6): 679-682)
(  0) 0) |
| [8] |
高德章, 侯遵泽, 唐建. 东海及邻区重力异常小波多尺度分解[J]. 地球物理学报, 2000, 40(6): 842-849 (Gao Dezhang, Hou Zunze, Tang Jian. Multiscale Analysis of Gravity Anomalies on East China Sea Adjacent Regions[J]. Chinese Journal of Geophysics, 2000, 40(6): 842-849)
(  0) 0) |
| [9] |
杨文采, 施志群, 侯遵泽. 离散小波变化与重力异常多重分解[J]. 地球物理学报, 2001, 44(4): 534-541 (Yang Wencai, Shi Zhiqun, Hou Zunze. Discrete Wavelet Transform for Multiple Decomposition of Gravity Anomalies[J]. Chinese Journal of Geophysics, 2001, 44(4): 534-541)
(  0) 0) |
| [10] |
秦前清, 杨宗凯. 实用小波分析[M]. 西安: 西安电子科技大学出版社, 1994 (Qin Qianqing, Yang Zongkai. Practical Wavelet Analysis[M]. Xi'an: Xidian University Press, 1994)
(  0) 0) |
| [11] |
宁津生, 汪海洪, 罗志才. 小波分析在大地测量中的应用及其进展[J]. 武汉大学学报:信息科学版, 2004, 29(8): 659-664 (Ning Jinsheng, Wang Haihong, Luo Zhicai. Applications of Wavelet Analysis in Geodesy and Its Progress[J]. Geomatics and Information Science of Wuhan University, 2004, 29(8): 659-664)
(  0) 0) |
| [12] |
重磁资料数据处理问题编写组. 重磁资料数据处理问题[M]. 北京: 地质出版社, 1997 (Editorial and Magnetic Data Processing Problem. Magnetic Data Processing Problem[M]. Beijing: Geological Publishing House, 1997)
(  0) 0) |
| [13] |
赵勇. 小波分析在重力异常分离中的应用研究[D]. 上海: 同济大学, 2003 (Zhao Yong. The Application of Wavelet Analysis in Gravity Anomaly Separation Research[D]. Shanghai: Tongji University, 2003)
(  0) 0) |
| [14] |
许闯. 多尺度重力反演方法及其在城市活动断层探测中的应用研究[D]. 武汉: 武汉大学, 2014 (Xu Chuang. Study on Multi-Scale Gravity Inverse Method and Its Application to Detect Urban Active Faults[D]. Wuhan: Wuhan University, 2014) http://cdmd.cnki.com.cn/Article/CDMD-10486-1015528752.htm
(  0) 0) |
| [15] |
侯遵泽, 杨文采. 中国重力异常的小波变换与多尺度分析[J]. 地球物理学报, 1997, 40(1): 85-95 (Hou Zunze, Yang Wencai. Wavelet Transform and Multi-Scale Analysis on Gravity Anomalies of China[J]. Chinese Journal of Geophysics, 1997, 40(1): 85-95)
(  0) 0) |
| [16] |
李健, 周云轩, 许惠平. 重力场数据处理中小波母函数的选择[J]. 物探与化探, 2001, 25(6): 410-417 (Li Jian, Zhou Yunxuan, Xu Huiping. The Selection of Wavelet Generating Functions in Data-Processing of Gravity Field[J]. Geophysical and Geochemical Exploration, 2001, 25(6): 410-417)
(  0) 0) |
| [17] |
Spector A, Grant F S. Statistical Models for Interpreting Aeromagnetic Data[J]. Geophysics, 1970, 35(2): 293-302 DOI:10.1190/1.1440092
(  0) 0) |
| [18] |
Syberg F J R. A Fourier Method for the Regional-Residual Problem of Potential FieIds[J]. Geophysical Prospecting, 1972, 20(1): 47-75 DOI:10.1111/gpr.1972.20.issue-1
(  0) 0) |
| [19] |
邱宁, 何展翔, 昌彦君. 分析研究基于小波分析与谱分析提高重力异常的分辨能力[J]. 地球物理学进展, 2007, 22(1): 210-214 (Qiu Ning, He Zhanxiang, Chang Yanjun. Ability of Improving Gravity Anomaly Resolution Based on Multiresolution Wavelet Analysis and Power Spectrum Analysis[J]. Progress in Geophysics, 2007, 22(1): 210-214)
(  0) 0) |
| [20] |
秦静欣, 郝天珧, 徐亚, 等. 南海及邻区莫霍面深度分布特征及其与各构造单元的关系[J]. 地球物理学报, 2011, 54(12): 3 171-3 183 (Qin Jingxin, Hao Tianyao, Xu Ya, et al. The Distribution Characteristics and the Relationship between the Tectonic Units of the Moho Depth in South China Sea and Adjacent Areas[J]. Chinese Journal of Geophysics, 2011, 54(12): 3 171-3 183)
(  0) 0) |
2. Xi'an Research Institute of Surveying and Mapping, 1 Mid-Yanta Road, Xi'an 710054, China;
3. State Key Laboratory of Geo-Information Engineering, 1 Mid-Yanta Road, Xi'an 710054, China;
4. Beijing Key Laboratory of Urban Spatial Information Engineering, 15 Yangfangdian Road, Beijing 100038, China
 2018, Vol. 38
2018, Vol. 38


