2. 中国科学院大学,北京市玉泉路甲19号,100049
重力观测通常会受到降雨、蒸发、地下水渗透和流动等影响,尤其是局部地区地下水变化的干扰[1-4]。因此,为防止地下水重力效应对地球物理学或动力学信号的掩盖,有必要对精密重力观测进行地下水改正。许多学者对地下水重力效应进行模拟[5-8],其中Kazama等[7]收集日本北部Isawa扇形地区水文、气象资料,利用一维地下水渗透方程,模拟该地区超导台站局部区域土壤含水率的时空分布及其导致的重力变化,取得与超导重力观测吻合较好的结果。但在其使用有限差分法解算渗透方程时采用显式差分格式,虽然计算简单,但受到收敛条件的限制,使得时间和空间步长的选取不自由。有限差分法除显式差分外,还有隐式差分和中心差分两种无条件收敛的差分格式[9]。本文在Kazama等[7]的基础上,探讨不同差分格式对地下水模拟结果以及相应重力改正的影响。
1 一维地下水渗透方程假设土壤性质均匀,且不考虑水平方向上的地下水流动,根据质量守恒原理和达西定律,有一维非饱和层的非线性渗透方程,即Richards方程[9-10]:
| $ \begin{array}{*{20}{c}} {\frac{{\partial \theta }}{{\partial t}} = \frac{\partial }{{\partial z}}\left[ {D\left( \theta \right)\frac{{\partial \theta }}{{\partial z}} + K\left( \theta \right)} \right] = }\\ {\frac{\partial }{{\partial z}}\left[ {D\left( \theta \right)\frac{{\partial \theta }}{{\partial z}}} \right] + \frac{{\partial K\left( \theta \right)}}{{\partial z}}} \end{array} $ | (1) |
式中,θ为土壤含水率,t为时间,z为垂直方向坐标。K(θ)和D(θ)分别为垂向渗透系数和扩散系数,均是含水率的函数[11-12],且与土壤性质参数有关。土壤性质参数包括垂向饱和渗透系数KS、饱和扩散系数DS、常数项a、b以及最大、最小含水率θmax和θmin,取值见表 1[7]。
|
|
表 1 土壤性质参数值 Tab. 1 The parameter values of soil property |
渗透方程的求解需要加入一定的边界条件和初始条件。这里给定的2个边界条件分别是地表处的渗透速率和地下水面处的含水率,初始条件设定为定水头稳定流条件下的稳态解[7]。
2 有限差分解算按深度把土壤均匀分为若干层,用θij、vij分别表示垂向第i层某时刻tj的含水率和渗透速率,利用有限差分法可将式(1)差分化。
2.1 显式差分Kazama等[7]的显式差分用时间上的向前差分公式代替
| $ \begin{array}{*{20}{c}} {\frac{{\theta _i^{j + 1} - \theta _i^j}}{{\Delta t}} = D_{i + 1/2}^j\frac{{\theta _{i + 1}^j - \theta _i^j}}{{\left[ {\Delta z} \right]^2}} + D_{i - 1/2}^j\frac{{\theta _{i - 1}^j - \theta _i^j}}{{{{\left[ {\Delta z} \right]}^2}}} + }\\ {\frac{{K_{i + 1/2}^j - K_{i + 1/2}^j}}{{\Delta z}}} \end{array} $ | (2) |
式中,θij+1是垂向第i层下一个时刻tj+1的含水率,可以由该时刻tj的含水率分布直接求得。式(2)的截断误差为O(Δt)+O(Δz)。
根据求解的地下水分布,利用牛顿引力定律和平面半无限空间近似计算地下水重力效应[7, 13]:
| $ {g_{\rm{w}}} = 2{\rm{ \mathsf{ π} }}{\rho _{\rm{w}}}G\Delta z \cdot \sum\limits_{i = 1}^N {{\theta _i}} $ | (3) |
式中,gw为地下水重力效应,Δz是水平含水层厚度,G为万有引力常数,ρw为水的密度。
式(2)中系数Di+1/2j、Di-1/2j、Ki+1/2j、Ki-1/2j都不是整数层的参数值,涉及到层间参数的取值问题。层间参数取值的加权公式有多种[14]。
1) 算术平均值:
| $ D_{i \pm 1/2}^j = \frac{{D_i^j + D_{i \pm 1}^j}}{2},K_{i \pm 1/2}^j = \frac{{K_i^j + K_{i \pm 1}^j}}{2} $ | (4) |
2) 几何平均值:
| $ D_{i \pm 1/2}^j = \sqrt {D_i^j \times D_{i \pm 1}^j} ,K_{i \pm 1/2}^j = \sqrt {K_i^j \times K_{i \pm 1}^j} $ | (5) |
3) 调和平均值:
| $ D_{i \pm 1/2}^j = 2\frac{{D_i^j \times D_{i \pm 1}^j}}{{D_i^j + D_{i \pm 1}^j}},K_{i \pm 1/2}^j = 2\frac{{K_i^j \times K_{i \pm 1}^j}}{{K_i^j + K_{i \pm 1}^j}} $ | (6) |
4) 上游值:
| $ D_{i \pm 1/2}^j = \left\{ {\begin{array}{*{20}{c}} {D_{i \pm 1}^j,D_{i \pm 1}^j \ge \theta _i^j}\\ {D_i^j,\theta _i^j > \theta _{i \pm 1}^j} \end{array}} \right.,K_{i \pm 1/2}^j = \left\{ {\begin{array}{*{20}{c}} {K_{i \pm 1}^j,\theta _{i \pm 1}^j \ge \theta _i^j}\\ {K_i^j,\theta _i^j > \theta _{i \pm 1}^j} \end{array}} \right. $ | (7) |
为比较不同加权公式的模拟效果,采用相同的差分格式、相同的模型参数、相同的初始条件和不同的层间加权公式,分别对渗透问题进行模拟计算,获得计算区域(地表至地下10 m)的土壤含水率分布及其重力效应。
图 1为不同层间参数加权公式对地下50 cm处含水率模拟结果的影响[7]。可以发现,Kazama等[7]的模拟结果与采用几何平均值法的结果差异为零,两者具有等价性;与上游值法差异最大,达到0.01;与调和平均值法差异次之;与算数平均值法差异更小,小于0.001。

|
图 1 不同层间参数加权公式对地下50 cm处含水率模拟结果的影响(2008-01-01起) Fig. 1 Influence of different weighting methods of determining interblock parameters on simulating of water content at the depth of 50 cm below |
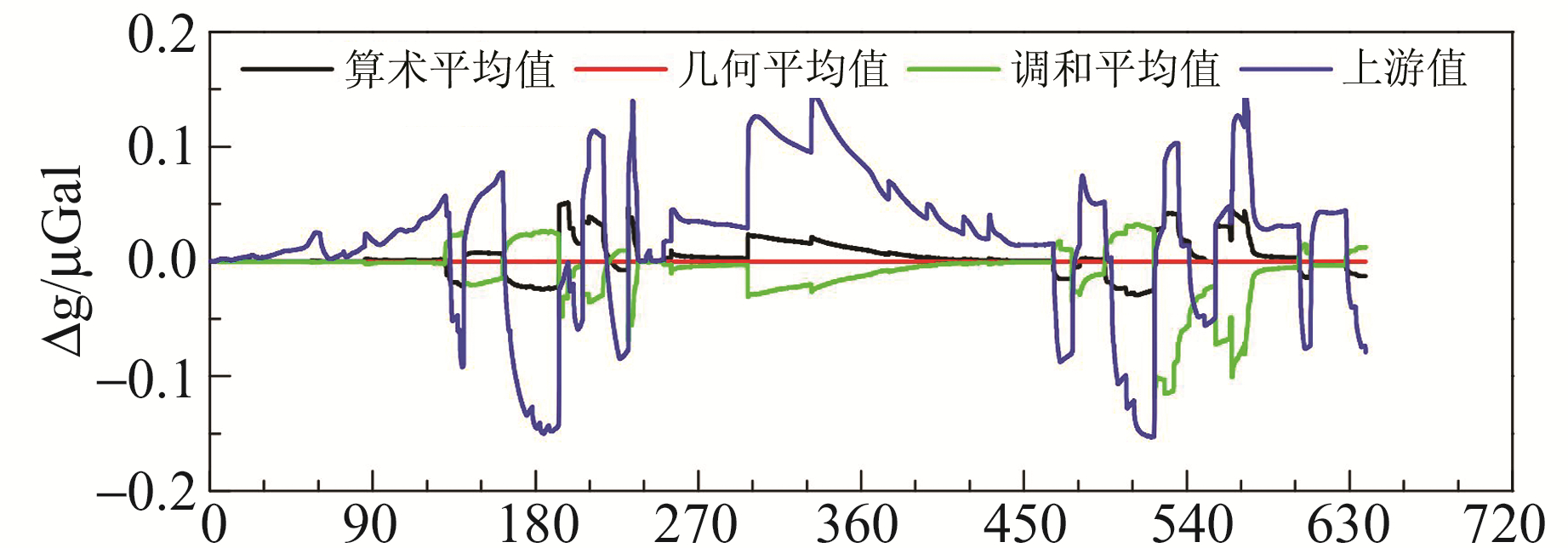
图 2为不同层间参数加权公式对地下水重力效应模拟的影响[7],表 2给出其标准差。可以发现,图 2与图 1有着类似的特征,Kazama等[7]的模拟结果与几何平均值法差异为零,而与上游值法差异最大,最大达0.15 μGal,标准差为0.064 μGal;与调和平均值法差异次之,标准差为0.024 μGal;与算数平均值法差异更小,小于0.05 μGal,标准差为0.015 μGal。相对于该台站变化幅度达8 μGal的地下水重力效应[7]来说,不同加权公式对地下水重力效应的影响在1.9%以内。
|
图 2 不同层间参数加权公式对地下水重力效应模拟的影响(2008-01-01起) Fig. 2 Influence of different weighting methods of determining interblock parameters on modeling of groundwater hydrological effect on gravity |
|
|
表 2 不同层间参数加权公式对地下水重力效应模拟影响的标准差 Tab. 2 Standard deviation of the influence of different weighting methods of determining interblock parameters on modeling of groundwater hydrological effect on gravity |
隐式差分用时间上的向后差分公式代替
| $ \begin{array}{*{20}{c}} {\frac{{\theta _i^{j + 1} - \theta _i^j}}{{\Delta t}} = D_{i + 1/2}^{j + 1}\frac{{\theta _{i + 1}^{j + 1} - \theta _i^{j + 1}}}{{{{\left[ {\Delta z} \right]}^2}}} + D_{i - 1/2}^{j + 1}\frac{{\theta _{i - 1}^{j + 1} - \theta _i^{j + 1}}}{{{{\left[ {\Delta z} \right]}^2}}} + }\\ {\frac{{K_{i + 1/2}^{j + 1} - K_{i - 1/2}^{j + 1}}}{{\Delta z}}} \end{array} $ | (8) |
式中,θi-1j+1、θij+1和θi+1j+1分别是垂向第i-1、i和i+1层下一个时刻tj+1的含水率,不可以由该式直接从时刻tj的含水率分布求得,而要通过联立形成三对角方程组,用追赶法进行求解。式(8)的截断误差也为O(Δt)+O(Δz)。
中心差分用时间上的中心差分公式代替
| $ \begin{array}{*{20}{c}} {\frac{{\theta _i^{j + 1} - \theta _i^j}}{{\Delta t}} = D_{i + 1/2}^{j + 1/2}\frac{{\theta _{i + 1}^{j + 1/2} - \theta _i^{j + 1/2}}}{{{{\left[ {\Delta z} \right]}^2}}} + }\\ {D_{i - 1/2}^{j + 1/2}\frac{{\theta _{i - 1}^{j + 1/2} - \theta _i^{j + 1/2}}}{{{{\left[ {\Delta z} \right]}^2}}} + \frac{{K_{i + 1/2}^{j + 1/2} - K_{i - 1/2}^{j + 1/2}}}{{\Delta z}}} \end{array} $ | (9) |
式中,θi-1j+1/2、θij+1/2和θi+1j+1/2分别是垂向第i-1、i和i+1层在tj+1/2时刻的含水率,用它们在tj+1和tj时刻含水率的平均值代替,对Di+1/2j+1/2、Di-1/2j+1/2、Ki+1/2j+1/2和Ki-1/2j+1/2采用同样的处理。该式也无法直接求解,需通过联立形成三对角方程组,用追赶法进行求解。式(9)的截断误差为O([Δt]2)+O(Δz),与式(8)具有相同的形式,两者的区别在于三对角方程的系数和常数项的不同。中心差分格式的截断误差比显式和隐式差分格式的要小,因此具有更高的精度。
由式(8)和(9)可知,隐式差分与中心差分公式中的扩散系数和渗透系数都是待求含水率的函数,因此这两方程是非线性的,这就牵涉到方程的线性化问题。常用的线性化方法有显式法、预测-校正法和迭代法[9]。
以隐式差分法为例,对3种线性化方法进行说明。显式法是用上一时刻的参数值Dij(或Kij)代替方程中的Dij+1(或Kij+1)。预测-校正法是先对未知数θij+1进行预测,然后在其基础上得到校正值。这里先用显式差分法得到tj+1时刻的预测值θij+1,根据土壤参数与含水率的关系曲线得到Dij+1(或Kij+1)的值,然后按隐式差分解算三对角方程组得到tj+1时刻的校正值θij+1。迭代法是先取tj时刻的Dij(或Kij)作为Dij+1(或Kij+1)的估计值,然后按照隐式差分解算三对角方程组,得到tj+1时刻含水率θij+1的第一次迭代值θij+1(1),根据θij+1(1)及土壤参数与含水率的关系曲线得到新的Dij+1(或Kij+1)值,再次按照隐式差分解算三对角方程组,得到第二次迭代值θij+1(2)。重复迭代过程,直到各层前后两次迭代值之差小于所规定的允许误差e为止,即
| $ \max \left| {\theta _i^{j + 1\left( m \right)} - \theta _i^{j + 1\left( {m - 1} \right)}} \right| \le e $ | (10) |
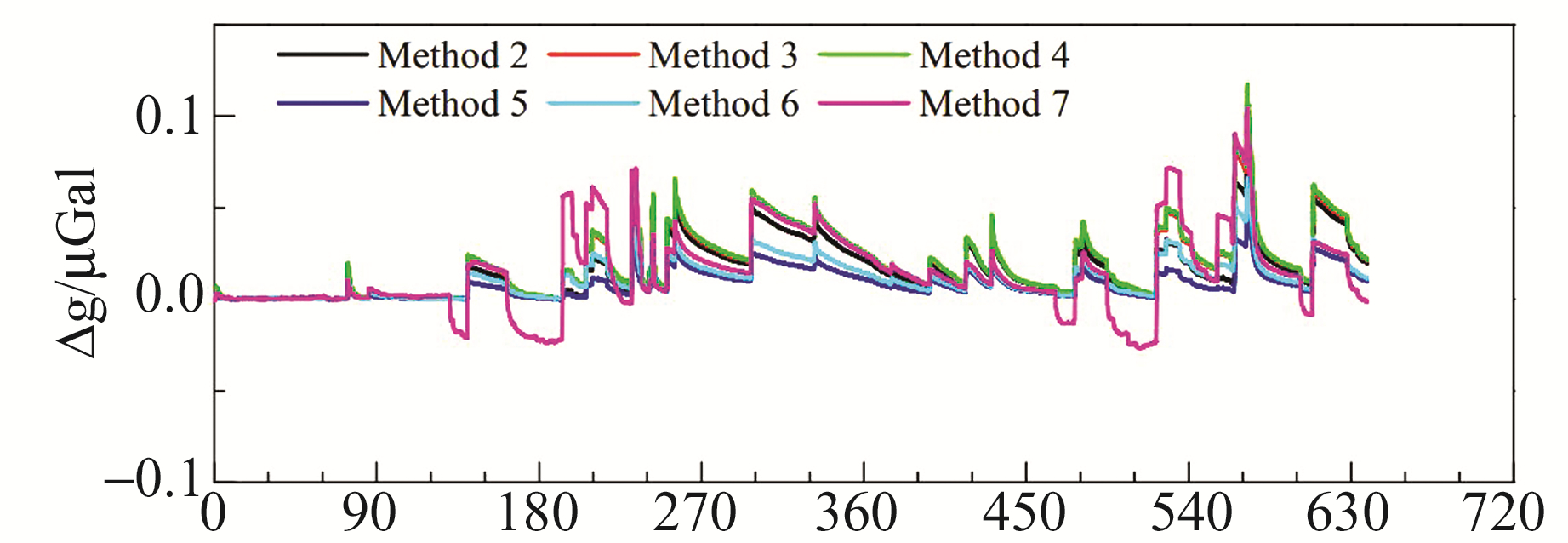
为比较不同差分形式和线性化方法的结果,采用相同的层间加权公式、模型参数、初始条件和不同的差分形式或线性化方法,分别对Kazama等[7]中的渗透问题进行模拟计算。表 3列出7种差分形式和线性化方法的组合,其中Kazama等[7]使用的是组合形式1(显式差分法)。图 3为不同差分格式和线性化方法组合形式对地下水重力效应模拟的影响,表 4给出了其标准差。从图 3看,各曲线随着时间增加慢慢分散,差异越来越大,说明各方法之间的差异存在一定的累积效应。在计算的639 d里,与组合形式1(显式差分法)的差异中,最大的是组合形式4(隐式迭代法),其最大差异值为0.12 μGal;而标准差最大的是组合形式7(中心迭代法),其差异的标准差为0.022 μGal。相对于该台站变化幅度达8 μGal的地下水重力效应而言,不同计算方法对地下水重力效应的影响在1.5%以内。
|
|
表 3 不同差分格式和线性化方法的组合形式 Tab. 3 Different combinations of differential schemes and linearization methods |
|
图 3 不同差分格式和线性化方法组合形式对地下水重力效应模拟的影响(2008-01-01起) Fig. 3 Influence of different differential schemes and linearization methods on modeling of groundwater hydrological effect on gravity |
|
|
表 4 不同差分格式和线性化方法组合对地下水重力效应模拟影响的标准差 Tab. 4 Standard deviation of the influence of different differential schemes and linearization methods on modeling of groundwater hydrological effect on gravity |
本文比较了不同差分格式对一维地下水渗透模拟结果及其相应地下水重力效应的影响。在日本北部Isawa扇形地区超导台站,不同层间参数加权公式最大能够引起约0.15 μGal的重力效应差异,影响在1.9%以内;不同差分格式和线性化方法组合最大能够引起约0.12 μGal的重力效应差异,影响在1.5%以内。该结果可为一维地下水模拟及重力效应改正算法的选取提供参考。
| [1] |
Crossley D, Hinderer J, Casula G, et al. Network of Superconducting Gravimeters Benefits a Number of Disciplines[J]. EOS Transactions American Geophysical Union, 1999, 80(11): 121-126
(  0) 0) |
| [2] |
Kroner C. Hydrological Effects on Gravity at the Geodynamic Observatory Moxa[J]. Journal of the Geodetic Society of Japan, 2001, 47(1): 353-358
(  0) 0) |
| [3] |
Abe M, Takemoto S, Fukuda Y, et al. Hydrological Effects on the Superconducting Gravimeter Observation in Bandung[J]. Journal of Geodynamics, 2006, 41(1-3): 288-295 DOI:10.1016/j.jog.2005.08.030
(  0) 0) |
| [4] |
Meurers B, Camp M, Petermans T. Correcting Superconducting Gravity Time-Series Using Rainfall Modelling at the Vienna and Membach Stations and Application to Earth Tide Analysis[J]. Journal of Geodesy, 2007, 81(11): 703-712 DOI:10.1007/s00190-007-0137-1
(  0) 0) |
| [5] |
Creutzfeldt B, Guntner A, Klugel T, et al. Simulating the Influence of Water Storage Changes on the Superconducting Gravimeter of the Geodetic Observatory Wettzell, Germany[J]. Geophysics, 2008, 73(6): WA95-WA104 DOI:10.1190/1.2992508
(  0) 0) |
| [6] |
Leiriāo S, He X, Christiansen L, et al. Calculation of theTemporal Gravity Variation from Spatially Variable Water Storage Change in Soils and Aquifers[J]. Journal of Hydrology, 2009, 365(3): 302-309
(  0) 0) |
| [7] |
Kazama T, Tamura Y, Asari K, et al. Gravity Changes Associated with Variations in Local Land-Water Distributions: Observations and Hydrological Modeling at Isawa Fan, Northern Japan[J]. Earth Planets and Space, 2012, 64(4): 309-331 DOI:10.5047/eps.2011.11.003
(  0) 0) |
| [8] |
贺前钱, 罗少聪, 孙和平, 等. 武汉九峰站地下水变化对重力场观测的影响[J]. 地球物理学报, 2016, 59(8): 2 765-2 772 (He Qianqian, Luo Shaocong, Sun Heping, et al. The Influence of Groundwater Changes on Gravity Observations at Jiufeng Station in Wuhan[J]. Chinese Journal Geophysics, 2016, 59(8): 2 765-2 772)
(  0) 0) |
| [9] |
薛禹群, 谢春红. 地下水数值模拟[M]. 北京: 科学出版社, 2007 (Xue Yuqun, Xie Chunhong. Numerical Modeling of Groundwater[M]. Beijing: Science Press, 2007)
(  0) 0) |
| [10] |
Bear J. Hydraulics of Groundwater[M]. New York: McGraw-Hill International Book Co, 1979
(  0) 0) |
| [11] |
Gardner W R, Mayhugh M S. Solutions and Tests of the Diffusion Equation for the Movement of Water in Soil[J]. Soil Sci Soc Am J, 1958, 22(3): 197-201 DOI:10.2136/sssaj1958.03615995002200030003x
(  0) 0) |
| [12] |
Davidson J M, Stone L R, Nielsen D R, et al. Field Measurement and Use of Soil-Water Properties[J]. Water Resour Res, 1969, 5(6): 1 312-1 321 DOI:10.1029/WR005i006p01312
(  0) 0) |
| [13] |
Camp M, Vanclooster M, Crommen O, et al. Hydrogeological Investigations at the Membach Station, Belgium, and Application to Correct Long Periodic Gravity Variations[J]. Journal of Geophysical Research:Solid Earth, 2006, 111(B10)
(  0) 0) |
| [14] |
Haverkamp R, Vauclin M. A Note on Estimating Finite Difference Interblock Hydraulic Conductivity Values for Transient Unsaturated Flow Problems[J]. Water Resources Research, 1979, 15(1): 181-187 DOI:10.1029/WR015i001p00181
(  0) 0) |
2. University of the Chinese Academy of Science, A19 Yuquan Road, Beijing 100049, China
 2018, Vol. 38
2018, Vol. 38


