解决测量中病态问题的有效途径是充分利用参数附加信息或先验信息(参数内在的相关性、精度、几何或物理信息)，对部分参数进行约束，从而保证参数解的唯一性和稳定性^[1-4]。随着测量手段的丰富，大量获取先验信息成为可能，使利用先验信息解决平差问题的可行性增高。然而，大地测量中有些先验信息有时仅是一个模糊数，只能用参数的可行空间、噪声范围等来描述^[5]。大地测量实际问题中，除了观测信息，还有参数本身或者前期研究中得到的一些附加的有用信息或者先验约束信息，将这些信息纳入参数估计过程，可以显著提高参数估计的效率。

近年来，研究人员基于先验信息对病态问题进行了广泛研究。文献[6]通过消除部分参数将等式约束病态问题转化为无约束问题，提出求解等式约束病态问题的诊断-正则化两步法；文献[7]针对模型中系数矩阵和约束矩阵同时存在病态性的问题，提出联合岭估计；文献[8]分析了不等式约束对平差结果的影响；文献[9]讨论了附加不等式约束的间接平差模型的3种经典算法——Lemke法、势函数法以及迭代乘子法，结果显示，将先验信息表达成不等式约束参与到平差中确实能改善平差的结果；文献[10]将参数带有不等式约束的最小二乘问题转化为凸二次规划问题，从而求出参数最小二乘估计的一般形式。以上研究利用的先验信息主要还是等式或不等式约束，所涉及的仅是最简单的先验信息，还不能处理一些复杂的模糊先验信息。本文以模糊数学为基础，用模糊数集描述参数向量中的模糊先验信息，建立约束方程参与平差解算，抑制估计过程中法方程的病态性，弥补现有等式约束、不等式约束理论难以利用模糊先验信息的缺陷。

1 模糊数理论

大地测量学中，先验信息可以分为两种:先验函数信息和先验随机信息。现阶段对先验信息的利用主要有等式约束、不等式约束以及验后估计等，它们分别从不同角度利用先验信息，提高参数估计效率。但大地测量学中先验信息的来源多样且复杂，充满许多不确定性^[11]，既包含数值与概念上的误差，也包含可度量误差与不可度量误差，无法用确切的数值来表示，不具有任何统计性质，现有的等式约束、不等式约束理论无法描述。

本文采用模糊数集来描述这些模糊先验信息。设A为R上的模糊集，μ_A(x)是模糊数A的隶属函数。若A满足条件：1)A是正规的模糊集，即至少存在x∈A，使μ_A(x)=1；2)模糊集A是凸的，即对任意实数x < y < z，都有μ_A(y)≥min{μ_A(x)，μ_A(z)}。则称A为一个模糊数^[12]。

在模糊数中，有一类特殊的模糊数——对称模糊数，表示为：

$ \mathit{\boldsymbol{A}} = {\left( {\alpha ,\delta } \right)_R} $

(1)

其中α为模糊数A的对称中心，δ为模糊幅度。A的隶属函数μ_A(x)表示x对模糊数A的隶属度。常见的对称模糊数分布有三角型、正态型等，如

$ {\mu _\mathit{\boldsymbol{A}}}\left( x \right) = \left\{ {\begin{array}{*{20}{c}} {1 - \frac{{\left| {x - \alpha } \right|}}{\delta }, - \delta \le x - \alpha \le \delta }\\ {0,\;\;\;\;\;\;其他} \end{array}} \right. $

(2)

表示的模糊数为三角模糊数，

$ {\mu _A}\left( x \right) = \exp - \left( {{{\left( {\frac{{x - \alpha }}{\delta }} \right)}^2}} \right),\delta > 0 $

(3)

表示的模糊数为正态模糊数^[13]。

将其引入到测量数据处理中，可以用模糊集来描述“观测值”到“真值”之间的变化过程。但通过分析经典误差分布理论，当选用对称模糊数来描述模糊先验信息时，其隶属函数需满足^[14]：1)关于x=α对称；2)μ(α)=1，即隶属函数在对称中心取最大值为1；3)在区间[α-δ，α]内，隶属函数严格单调递增；在区间[α，α+δ]内，严格单调递减；在区间(-∞，α-δ)∪(α+δ, +∞)内，μ(x)=0。

图 1表示观测信息的一个离散集合L=[L₁L₂…L_n]。若进行无限次观测，便可以将图 1表示成类似于图 2的连续集合，即以真值为圆心、观测值最大偏差为半径的圆。将其用数学符号表示，就是一个模糊数：

$ \mathit{\boldsymbol{L}} = \left[ {{L_0},{V_{\max }}} \right] $

(4)

式中，L₀为对称中心，可理解为真值；V_max为模糊幅度，等于观测值最大偏差，表示观测值变化范围。因此，可以将模糊先验信息描述为：

$ \mathit{\boldsymbol{X}} \in {\left[ {{X_0},{\delta _X}} \right]_X},\mathit{\boldsymbol{X}} \sim \mu \left( x \right) $

(5)

式中，X₀、δ_X分别表示根据先验信息得知的参数中心值及变化范围，μ(x)为隶属度函数。

2 约束模型及解算

基于模糊先验信息的平差模型可以表示为:

$ \left\{ \begin{array}{l} \mathit{\boldsymbol{L}} = \mathit{\boldsymbol{AX}} + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}\\ \mathit{\boldsymbol{X}} \in {\left[ {{X_0},{\delta _X}} \right]_X},\mathit{\boldsymbol{X}} \sim \mu \left( x \right) \end{array} \right. $

(6)

相应的误差方程为：

$ \left\{ \begin{array}{l} \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{AX}} - \mathit{\boldsymbol{L}}\\ \mathit{\boldsymbol{X}} \in {\left[ {{X_0},{\delta _X}} \right]_X},\mathit{\boldsymbol{X}} \sim \mu \left( x \right) \end{array} \right. $

(7)

式中，X₀为先验信息提供的参数中心值；δ_X为模糊幅度，等于参数的最大偏差，表示X的变化范围。传统最小二乘估计准则为观测值残差的加权平方和最小，即

$ \sum\limits_{i = 1}^n {{p_i}v_i^2} = \min $

(8)

由式(8)可知，最小二乘准则函数只与观测值残差有关，忽略了参数X的分布规律与统计性质，容易造成解不稳定，即病态性问题。为了得到稳定解，对参数X施加“准确度最高”约束，即“在参数X准确度最高的条件下观测值的残差平方和最小”。由前面可知，参数X的准确度最高，可以通过使其隶属度达到最大值来实现：

$ {\mu _\mathit{\boldsymbol{A}}}\left( \mathit{\boldsymbol{X}} \right) = \max $

(9)

本文以正态模糊数的隶属函数(3)为例，对其隶属函数取最大值：

$ {\mu _\mathit{\boldsymbol{A}}}\left( x \right) = \exp - \left( {{{\left( {\frac{{x - \alpha }}{\delta }} \right)}^2}} \right) = \max $

(10)

由于式(10)指数项恒为负，则式(10)等价于：

$ {\left( {\frac{{x - \alpha }}{\delta }} \right)^2} = \min $

(11)

联立式(8)与式(11)，构造新的平差准则：

$ \sum\limits_{i = 1}^n {{p_i}v_i^2} + \sum\limits_{j = 1}^t {{{\left( {\frac{{{X_j} - {\alpha _j}}}{{{\delta _j}}}} \right)}^2}} = \min $

(12)

式中，v_i为观测值残差；α_j为参数近似值；δ_j为模糊幅度，等于参数最大残差。令

$ {w_j} = \frac{1}{{\delta _{{X_j}}^2}} $

(13)

式中，w_j表示先验信息的权。为避免出现δ_Xj=0导致w_j无限大的情况，可将式(13)写成：

$ {w_j} = \frac{1}{{\delta _{{X_j}}^2 + \tau }} $

(14)

式中，0 < τ < 1。文献[14]给出其取值经验公式：

$ \tau = \frac{{\sum\limits_{j = 1}^t {\left| {{X_j} - \alpha } \right|} }}{{10t\left| {{V_{\max }}} \right|}} $

(15)

取W=diag(w₁，w_2, ，…w_t)，则可将式(12)写成矩阵形式：

$ {\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{PV}} + \mathit{\boldsymbol{V}}_\mathit{\boldsymbol{X}}^{\rm{T}}\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{V}}_\mathit{\boldsymbol{X}}} = \min $

(16)

式中，V为观测值残差；P为观测值权阵；V_X = X - α，可理解为参数X的残差。将式(16)对参数X求偏导并令其等于0，得：

$ 2{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{PA}} + 2\mathit{\boldsymbol{V}}_\mathit{\boldsymbol{X}}^{\rm{T}}W = 0 $

(17)

将误差方程式(7)代入式(17)得：

$ \left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PA}} + \mathit{\boldsymbol{W}}} \right)\mathit{\boldsymbol{X}} - \left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PA}} + \mathit{\boldsymbol{W\alpha }}} \right) = 0 $

(18)

α为参数对称中心，与$ {{w}_{j}}=\frac{1}{\delta _{{{\mathit{\boldsymbol{X}}}_{j}}}^{2}} $均从先验信息中获取。令N = A^TPA + W，则参数解向量及其协因数阵分别为：

$ \mathit{\boldsymbol{X}} = {\mathit{\boldsymbol{Q}}_{\mathit{\boldsymbol{\tilde X\tilde X}}}}\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PL}} + \mathit{\boldsymbol{W\alpha }}} \right) $

(19)

$ {\mathit{\boldsymbol{Q}}_{\mathit{\boldsymbol{\tilde X\tilde X}}}} = {\mathit{\boldsymbol{N}}^{ - 1}} $

(20)

3 算例分析 3.1 算例1

采用文献[15]中的算例。这是一个模拟病态问题，其中设计矩阵为：

$ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {2.0000}&{ - 5.0000}&{1.0000}&{1.0000}&{ - 9.5000}\\ { - 2.0000}&{4.0000}&{1.0000}&{ - 1.0500}&{8.5000}\\ { - 2.0000}&{1.0000}&{1.0000}&{ - 1.0000}&{2.4000}\\ { - 1.0000}&{2.5000}&{4.0000}&{ - 0.5000}&{7.0000}\\ { - 1.0000}&{3.2000}&{4.0000}&{ - 0.5000}&{8.4000}\\ {1.0000}&{1.0000}&{ - 3.0000}&{0.4000}&{0.4900}\\ {3.0000}&{7.0000}&{ - 3.0000}&{1.5000}&{12.7000}\\ {5.0000}&{ - 1.0000}&{2.0000}&{2.5000}&{ - 3.0000}\\ {4.0000}&{2.0000}&{ - 2.0000}&{2.0100}&{3.0000}\\ {4.0000}&{3.0000}&{ - 2.0000}&{2.0000}&{5.0000} \end{array}} \right] $

法方程系数阵N = A^TA的条件数为1.289 2×10⁵，严重病态。未知参数有5个，其真值为X=[1 1 1 1 1]^T，观测噪声Δ~N(0, σ²I), σ=1，由随机数发生器产生。现对算例加以补充，设已知参数的上下界：

$ \left\{ \begin{array}{l} - 0.8 \le {X_1} \le 1.2\\ 0.7 \le {X_1} \le 1.7\\ - 2.5 \le {X_3} \le 1.5\\ 1 \le {X_4} \le 2\\ 0 \le {X_5} \le 6 \end{array} \right. $

(21)

将其作为参数的先验信息。采用模糊数来描述先验信息。取$ \alpha =\frac{{{X}_{U}}+{{X}_{L~}}}{2}$作为模糊数的对称中心，$ \sigma =\frac{{{X}_{U}}-{{X}_{L~}}}{2} $为模糊幅度，式中X_U、X_L为参数上下界。将先验信息表示为模糊数形式如式(22)并进行计算，结果见表 1。为了验证新方法的效果，还采用最小二乘、岭估计、截断奇异值法进行比较，比较计算的$ \mathit{\boldsymbol{\hat{X}}} $与真值X的差的范数$ \left\| {\Delta \mathit{\boldsymbol{\hat X}}} \right\| = \left\| {\mathit{\boldsymbol{\hat X}} - \mathit{\boldsymbol{X}}} \right\| $的大小。计算结果列于表 1。

$ \mathit{\boldsymbol{X}} \in \left[ {\begin{array}{*{20}{c}} {\left( {0.2,1} \right)}\\ {\left( {1.2,0.5} \right)}\\ {\left( { - 0.5,2} \right)}\\ {\left( {1.5,0.5} \right)}\\ {\left( {3,3} \right)} \end{array}} \right] $

(22)

由表 1可知，新方法的$ {\mathit{\boldsymbol{\hat{X}}}} $较接近真值，$ \left\| \Delta \mathit{\boldsymbol{\hat{X}}} \right\| $远小于最小二乘法，且低于岭估计及截断奇异值法，说明新方法不仅能够抑制法方程的病态性，还有较高的精度。

3.2 算例2

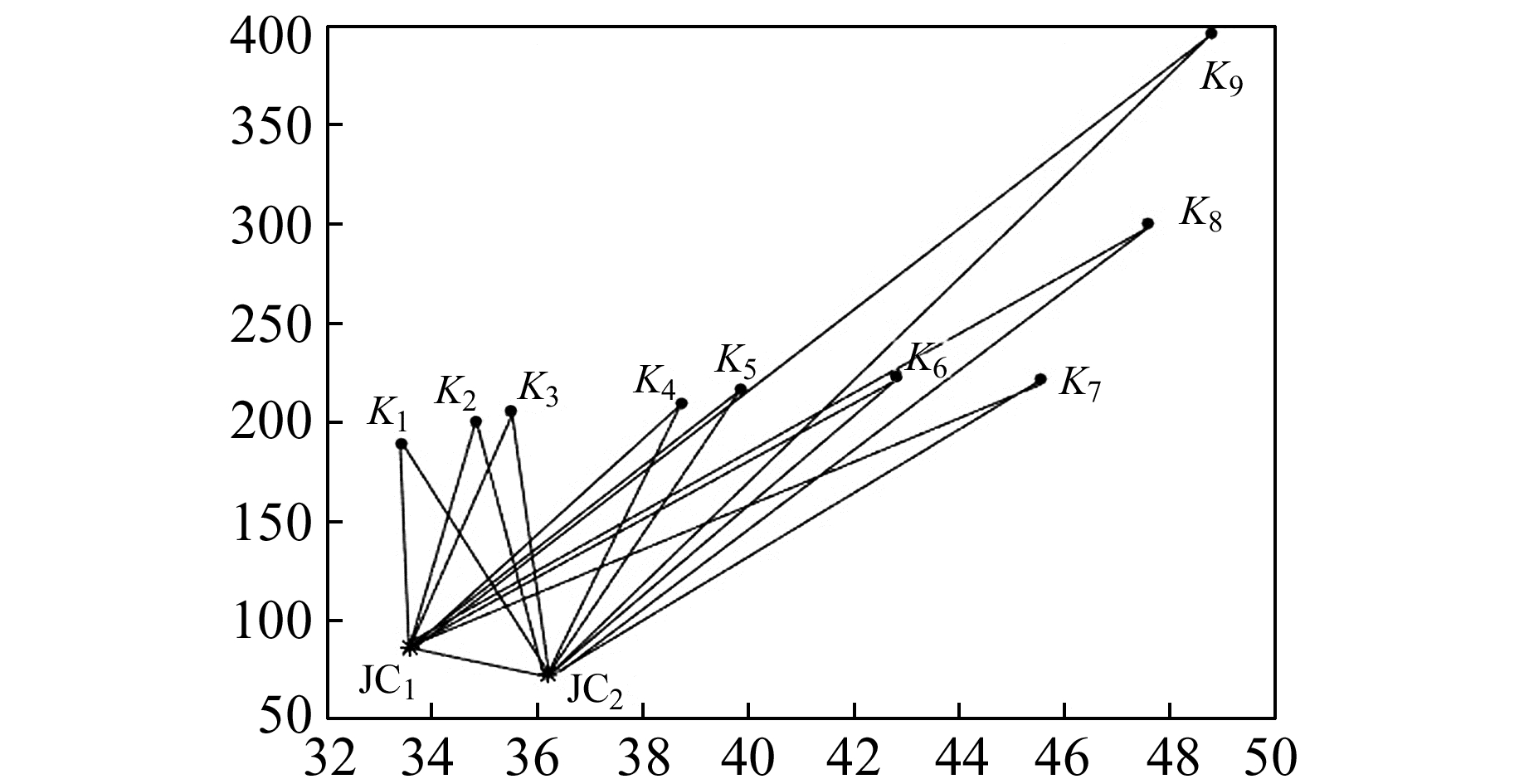
为了验证算法的可行性，本文根据某工程基坑水平位移监测数据模拟了一个测边网算例，如图 3所示。该工程在施工期间，采用徕卡TC402型全站仪(测角精度为2″，测距误差为2 mm+2×10^-6)对基坑内的监测点坐标进行周期性重复测量，得到一系列坐标数据。在图 3中的模拟测边网中，未知点JC₁、JC₂为该工程的两个监测点，K₁、K₂、…、K₉为9个模拟已知点，其坐标列于表 2。在实际测量中，由于观测条件不完善，导致观测距离与其理论值存在差异。本文利用MATLAB对各点间计算距离施加模拟噪声作为观测距离，也列于表 2，其中两个未知点之间的距离为d_{JC1, JC2}=14.060 4 m。要求根据观测距离确定两个未知点的坐标。

该算例中法矩阵的条件数为3.883 3×10³，法矩阵存在严重病态问题。

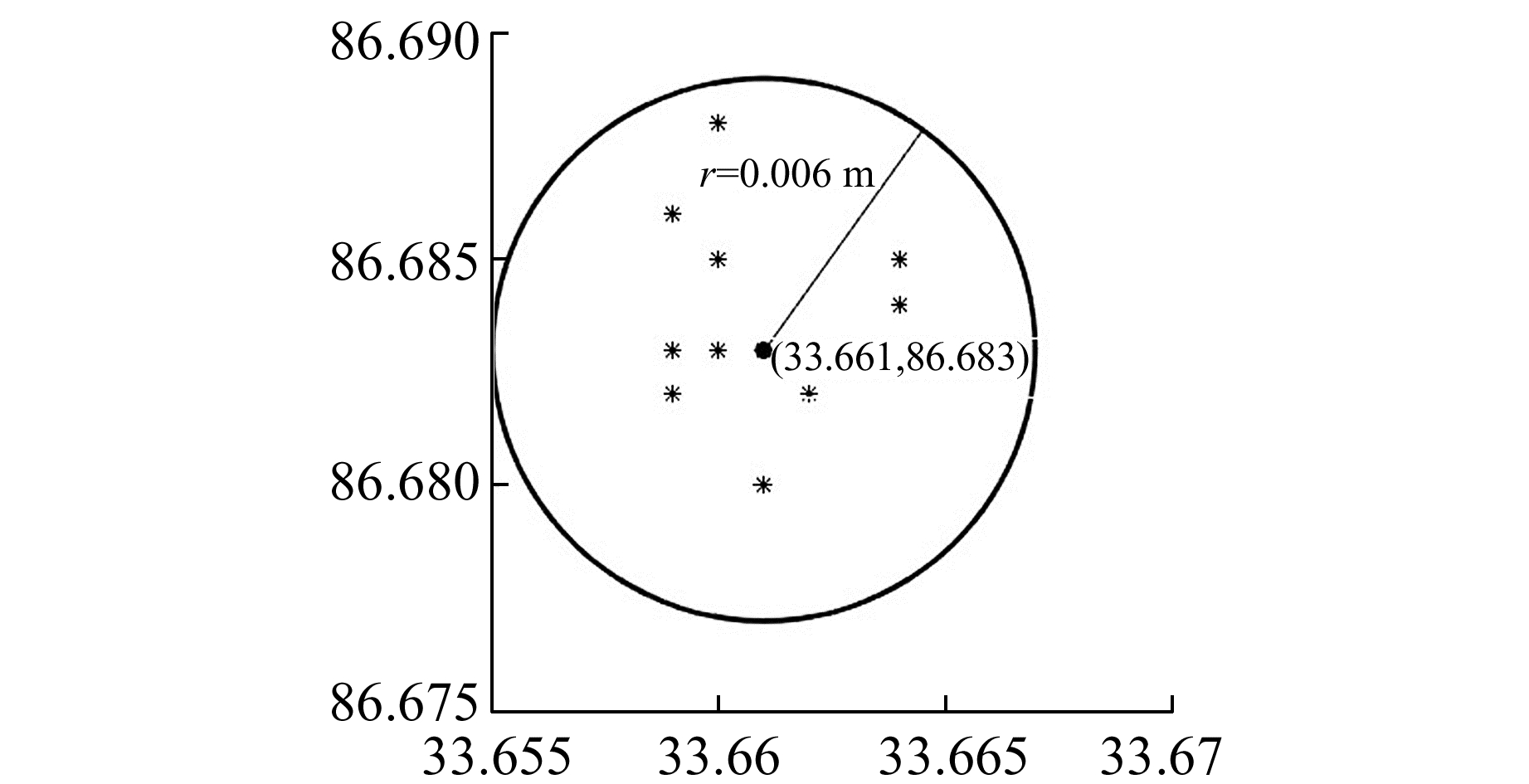
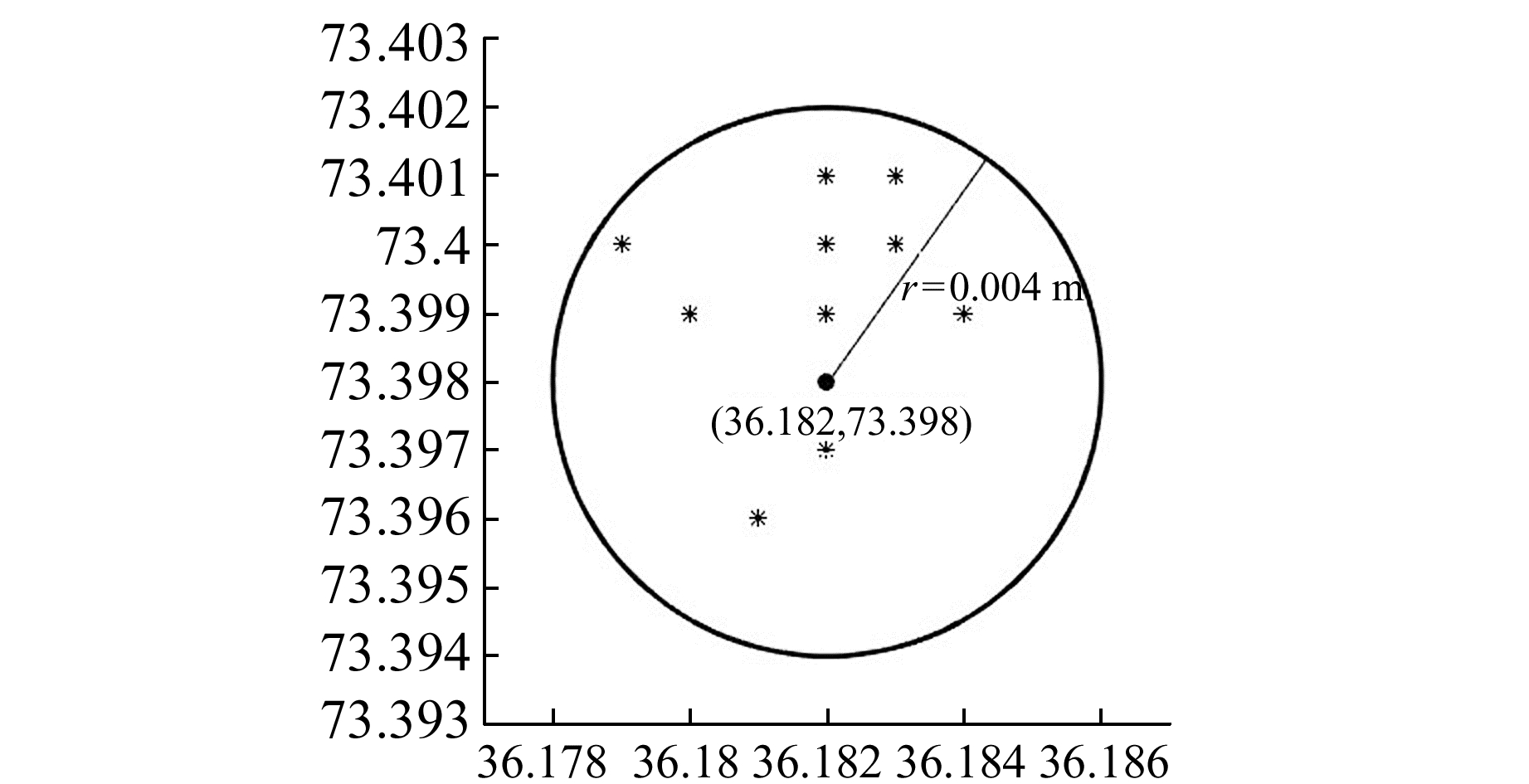
由于该工程在施工期间对监测点坐标进行了周期性重复测量，因此可将往期测量得到的坐标信息作为先验信息。每隔4期选取一次，共10期，其分布如图 4、图 5所示。采用模糊数对其描述，取中心坐标$ \left( {{X}_{0}}, {{Y}_{0}} \right)=\left( \frac{{{X}_{\text{max}}}-{{X}_{\text{min}}}}{2}, \frac{{{Y}_{\text{max}}}-{{Y}_{\text{min}}}}{2} \right) $作为对称中心α，模糊幅度$ \delta =\text{ma}{{\text{x}}_{i=1, 2\ldots 10}}\left\{ \sqrt{{{({{X}_{i}}-{{X}_{0}})}^{2}}+{{\left( {{Y}_{i}}-{{Y}_{0}} \right)}^{2}}} \right\} $，则参数X的先验信息可表示为[(33.661，0.006)(86.683，0.006)(36.182，0.004)(73.398，0.004)]^T。将其代入新方法计算，结果列于表 3(单位m)。为了验证新方法的效果，本文采用最小二乘、岭估计、截断奇异值法进行比较。在计算过程中，可取中心坐标(X₀，Y₀)为坐标近似值，比较计算的$ \mathit{\boldsymbol{\hat{X}}} $与实测值X的差的范数$ \left\| \Delta \mathit{\boldsymbol{\hat{X}}} \right\|=\left\| \mathit{\boldsymbol{\hat{X}}}-\mathit{\boldsymbol{X}} \right\| $的大小。计算结果列于表 3。

通过以上结果的对比分析可以得到结论：

1) 由表 3可知，本文提出的方法相对于最小二乘估计，参数估计值X更靠近真值$ {\mathit{\boldsymbol{\hat{X}}}} $; 未知参数差的范数为0.003 0，远小于最小二乘的计算结果1.505 0，说明本文提出的新方法已抑制了法方程的病态性，得到更加稳定的参数解。

2) 计算结果显示，新方法的精度优于岭估计，这是由于岭估计的实质是利用数学手段，通过对法矩阵的奇异值进行修正来抑制法方程的病态性，并没有考虑病态问题产生的原因。而本文提出的方法，考虑到测量学中病态性问题多由观测信息不足造成，因此采用模糊数集来描述测量学中的模糊先验信息，并将其纳入平差模型，根据其模糊幅度δ对参数进行定权、约束，从而弥补了观测信息的不足，抑制了法方程的病态性。

3) 本文所提方法较之截断奇异值法仍有更加准确的参数估值，其参数差的范数为0.003 0，小于截断奇异值法计算得到的结果0.643 9。因为截断奇异值法是通过删除模型参数中的不可靠部分来减小解的方差，而本文方法恰恰相反，是利用先验信息对模型参数加以补充，以此来缩短解区间并抑制方程的病态性。“一删一补”之间，估计精度得到显著提高。

4 结语

本文论述了基于模糊先验信息约束下的平差准则，尝试采用模糊数集来描述模糊先验信息，对参数X施加“准确度最高”约束，纳入平差模型参与解算，并给出了参数的计算公式，克服了平差过程中法方程病态的问题，弥补了大地测量学中模糊先验信息难以利用的缺陷。实例显示，该方法与岭估计及截断奇异值法相比，有更高的参数估计精度，可以应用于大地测量学的数据处理。