变量中含有误差(errors-in-variables, EIV)的参数估计模型广泛存在于测量数据处理中,能够顾及模型随机性质的拉格朗日算法的建立[1-2]使得EIV模型在测量数据处理中得到广泛应用[3-5]。众多学者将经典模型中存在的抗差估计、不适定模型的正则化、附有约束条件模型的参数估计引入到EIV模型中进行讨论[6-9]。
在测量数据处理中,模型的不适定性主要是指模型参数的解不唯一与不稳定。模型参数解不稳定是由于模型法方程矩阵的条件数很大,求逆不稳定,使得观测值的微小变动可引起参数解的巨大变化,即解的不稳定。具有不稳定参数解的模型称为病态模型,高程异常拟合模型可能会出现病态性。岭估计是经典病态模型正则化的一种有效方法,被应用在病态EIV模型的正则化中[10-11]。EIV模型的参数估计算法是应用参数近似系数矩阵中含有的误差,具有降正则化的特点[7],因此,病态EIV模型的参数估计算法既要实现降正则化,又要实现正则化。基于岭估计的病态EIV模型参数估计算法没有顾及这方面的影响。
应用法方程矩阵的特征向量构建病态高程异常拟合模型的正则化矩阵,克服了传统算法根据单一正则化参数既要实现模型正则化,又要实现模型降正则化存在的缺陷。应用实测数据对所建立算法的有效性进行验证,并与传统算法进行比较。
1 高程异常拟合模型与其正则化算法 1.1 高程异常拟合模型应用GNSS获得的基线向量可以得到控制点的大地高(差),它是点沿法线方向到参考椭球的距离。相对于根据点沿铅垂线到似大地水准面距离定义的高程,大地高仅具有几何意义,不具有物理意义,它并不能够作为判断地形起伏的依据。忽略点的法线与铅垂线间的垂线偏差,高程异常是参考椭球面与大地水准面之间的差距,在较小的区域范围内,点的高程异常值近似等于其大地高差减去高程。在工程测量中,为应用大地高获得高程的近似值,应用数学模型拟合测区的高程异常。以二次多项式模型为例:
| $ {\delta _i} = {b_0} + {b_1}{x_i} + {b_2}{y_i} + {b_3}{x_i}{y_i} + {b_4}x_i^2 + {b_5}y_i^2 $ | (1) |
式中,δi为控制点的高程异常,(xi,yi)为平面坐标,(b0,b1,b2,b3,b4,b5)为拟合模型的参数。设观测数为n(n > 6),将式(1)表示为:
| $ \mathop {\left[ {\begin{array}{*{20}{c}} {{\delta _1}}\\ \vdots \\ {{\delta _n}} \end{array}} \right]}\limits_\mathit{\boldsymbol{l}} = \mathop {\left[ {\begin{array}{*{20}{c}} 1&{{x_1}}&{{y_1}}&{{x_1}{y_1}}&{x_1^2}&{y_1^2}\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots \\ 1&{{x_n}}&{{y_n}}&{{x_n}{y_n}}&{x_n^2}&{y_n^2} \end{array}} \right]}\limits_\mathit{\boldsymbol{B}} \mathop {\left[ {\begin{array}{*{20}{c}} {{b_0}}\\ {{b_1}}\\ {{b_2}}\\ {{b_3}}\\ {{b_4}}\\ {{b_5}} \end{array}} \right]}\limits_\mathit{\boldsymbol{x}} $ | (2) |
式中,l为观测向量,B为系数矩阵,x为参数向量。
应用最小二乘准则,建立高斯-马尔可夫模型:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{v}} = \mathit{\boldsymbol{Bx}} - \mathit{\boldsymbol{l}},\mathit{\boldsymbol{v}} \sim N\left( {0,\sigma _0^2{\mathit{\boldsymbol{P}}^{ - 1}}} \right)\\ {\mathit{\boldsymbol{v}}^{\rm{T}}}\mathit{\boldsymbol{Pv}} = \min \end{array} \right. $ | (3) |
式中,v为观测向量中含有的误差向量,σ02为单位权方差,P为观测向量的权矩阵。参数的最小二乘解与其单位权方差的估值为:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\hat x}} = {\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB}}} \right)^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{Pl}}\\ \hat \sigma _0^2 = \frac{{{\mathit{\boldsymbol{v}}^{\rm{T}}}\mathit{\boldsymbol{Pv}}}}{{n - 6}} \end{array} \right. $ | (4) |
高程异常拟合模型的系数矩阵由观测元素或者观测元素的函数组成,系数矩阵中不可避免地含有观测误差。因此,高程异常拟合模型是EIV模型,此时,参数的最小二乘解不再具有最优、无偏的性质。为解决EIV模型的参数估计问题,最小二乘准则被拓展为总体最小二乘准则,应用拉格朗日函数,得到参数的总体最小二乘估值为[1]:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{v}}^{\rm{T}}}\mathit{\boldsymbol{Pv}} + {\mathit{\boldsymbol{b}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_B}\mathit{\boldsymbol{b}} = \min \\ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat x}} = \left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\left( {\mathit{\boldsymbol{Q}} + {{\left( {\left( {{{\mathit{\boldsymbol{\hat x}}}^{\rm{T}}}{\mathit{\boldsymbol{Q}}_0}\mathit{\boldsymbol{\hat x}}} \right){\mathit{\boldsymbol{Q}}_b}} \right)}^{ - 1}}\mathit{\boldsymbol{B}} - } \right.} \right.}\\ {{{\left. {\mathit{\boldsymbol{\hat \delta }}{\mathit{\boldsymbol{Q}}_0}} \right)}^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}{{\left( {\mathit{\boldsymbol{Q}} + \left( {{{\mathit{\boldsymbol{\hat x}}}^{\rm{T}}}{\mathit{\boldsymbol{Q}}_0}\mathit{\boldsymbol{\hat x}}} \right){\mathit{\boldsymbol{Q}}_b}} \right)}^{ - 1}}\mathit{\boldsymbol{l}}} \end{array} \end{array} \right. $ | (5) |
式中,b为系数矩阵中含有的误差矩阵EB按列拉直得到的列向量,PB为系数矩阵的权矩阵,Q、Q0、Qb为协因数阵,其具体的定义方法与参数迭代算法见参考文献[1]。
1.2 病态EIV模型的岭估计算法岭估计是病态模型正则化的有效算法,它是对病态模型的法矩阵附加一个对角矩阵,改善法矩阵的特征值接近于零的程度:
| $ \mathit{\boldsymbol{\hat x}} = {\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB}} + k\mathit{\boldsymbol{I}}} \right)^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{Pl}} $ | (6) |
式中,k为岭参数,I为单位矩阵。在关注病态EIV模型的同时,将岭估计应用至病态EIV模型的正则化。应用拉格朗日乘数,构建目标函数:
| $ \begin{array}{l} \mathit{\boldsymbol{\varphi }} = {\mathit{\boldsymbol{v}}^{\rm{T}}}\mathit{\boldsymbol{Pv}} + {\mathit{\boldsymbol{b}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_B}\mathit{\boldsymbol{b}} + \alpha \left( {{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{x}}} \right) + \\ 2{\lambda ^{\rm{T}}}\left( {\mathit{\boldsymbol{l}} + \mathit{\boldsymbol{v}} - \mathit{\boldsymbol{Bx}} - {\mathit{\boldsymbol{E}}_B}\mathit{\boldsymbol{x}}} \right) = \min \end{array} $ | (7) |
式中,a为正则化参数。等权条件下,得到参数的正则化估值为:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\hat x}} = {\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B}} + k\mathit{\boldsymbol{I}}} \right)^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{l}}\\ k = \alpha \left( {1 + {{\mathit{\boldsymbol{\hat x}}}^{\rm{T}}}\mathit{\boldsymbol{\hat x}}} \right) - \frac{{{{\left( {\mathit{\boldsymbol{l}} - \mathit{\boldsymbol{B\hat x}}} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{l}} - \mathit{\boldsymbol{B\hat x}}} \right)}}{{\left( {1 + {{\mathit{\boldsymbol{\hat x}}}^{\rm{T}}}\mathit{\boldsymbol{\hat x}}} \right)}} \end{array} \right. $ | (8) |
参数估值的迭代算法见参考文献[10]。EIV模型的总体最小二乘算法是用参数近似系数矩阵中含有的误差,以基于奇异值分解的算法为例,参数的估值为:
| $ \mathit{\boldsymbol{\hat x}} = {\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B}} + \sigma _{n + 1}^2{\mathit{\boldsymbol{I}}_u}} \right)^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{l}} $ | (9) |
式中,σn+1为增广矩阵[B l]的第n+1个奇异值。当法矩阵病态时,总体最小二乘算法会加重模型的病态性,其具有降正则化的性质。以文献[12]中的实验数据为例,其法矩阵BTB的条件数为20 837,总体最小二乘法方程中(BTB-σn+12In)的条件数为5.455 5×108,法矩阵的病态性更加严重。EIV模型的总体最小二乘算法中,近似系数矩阵误差的参数是关于正则化参数的函数。因此,在病态EIV的正则化中,正则化参数既要具有降正则化的性质,又要具有正则化的性质,现有关于病态EIV模型正则化的研究成果没有顾及这方面因素的影响。
2 病态EIV模型的广义岭估计算法病态模型的岭估计是Tikhonov函数的简化形式,测量数据处理中的不适定模型可以用Tikhonov函数进行概括[13]。不适定模型的概括模型可以表示为:
| $ {\mathit{\boldsymbol{v}}^{\rm{T}}}\mathit{\boldsymbol{Pv}} + {\mathit{\boldsymbol{b}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_B}\mathit{\boldsymbol{b}} + \alpha \mathit{\Omega }\left( \mathit{\boldsymbol{x}} \right) = \min $ | (10) |
式中,Ω(x)为稳定泛函,其不同的取值可以概括不同的正则化方法。本文应用约束矩阵实现病态EIV模型的正则化,减小正则化参数对模型正则化的影响。对EIV模型的法矩阵进行特征值分解:
| $ {\left( {\mathit{\boldsymbol{B}} + {\mathit{\boldsymbol{E}}_B}} \right)^{\rm{T}}}\mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{B}} + {\mathit{\boldsymbol{E}}_B}} \right) = \mathit{\boldsymbol{G \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{G}}^{\rm{T}}} $ | (11) |
式中,Λ为特征值构成的对角矩阵,G为特征向量构成的矩阵。对法矩阵的较小特征值进行选择性修正,可以有效降低病态模型参数估计的方差,减小正则化算法对参数估值的扰动[14]。根据文献[7]的总体最小二乘正则化解,应用法矩阵较小特征值对应的特征向量Gi,得到参数的广义解:
| $ \mathit{\boldsymbol{\hat x}} = {\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB}} - \sigma _{n + 1}^2{\mathit{\boldsymbol{I}}_n} + {\mathit{\boldsymbol{G}}_i}\mathit{\boldsymbol{G}}_i^{\rm{T}}} \right)^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{Pl}} $ | (12) |
根据EIV模型的极值函数估值,建立病态EIV模型正则化的迭代算法。
1) 计算拟合模型参数的初值:
| $ \mathit{\boldsymbol{\hat x}} = {\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB}} + {\mathit{\boldsymbol{G}}_i}\mathit{\boldsymbol{G}}_i^{\rm{T}}} \right)^{ - 1}}\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{Pl}}} \right) $ | (13) |
2) 计算拟合模型参数总体最小二乘初值:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat x}} = \left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}{{\left( {\mathit{\boldsymbol{Q}} + \left( {{{\mathit{\boldsymbol{\hat x}}}^{\rm{T}}}{\mathit{\boldsymbol{Q}}_0}\mathit{\boldsymbol{\hat x}}} \right){\mathit{\boldsymbol{Q}}_b}} \right)}^{ - 1}}\mathit{\boldsymbol{B}} + } \right.}\\ {{{\left. {{\mathit{\boldsymbol{G}}_i}\mathit{\boldsymbol{G}}_i^{\rm{T}}} \right)}^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}{{\left( {\mathit{\boldsymbol{Q}} + \left( {{{\mathit{\boldsymbol{\hat x}}}^{\rm{T}}}{\mathit{\boldsymbol{Q}}_0}\mathit{\boldsymbol{\hat x}}} \right){\mathit{\boldsymbol{Q}}_b}} \right)}^{ - 1}}\mathit{\boldsymbol{l}}} \end{array} $ | (14) |
3) 应用模型参数的估值,计算拉格朗日乘数的估值与改正数的估值:
| $ {\lambda _i} = {\left( {\mathit{\boldsymbol{Q}} + \left( {\mathit{\boldsymbol{\hat x}}_i^{\rm{T}}{\mathit{\boldsymbol{Q}}_0}{{\mathit{\boldsymbol{\hat x}}}_i}} \right){\mathit{\boldsymbol{Q}}_b}} \right)^{ - 1}}\left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{B}}{{\mathit{\boldsymbol{\hat x}}}_i}} \right) $ | (15) |
| $ {\mathit{\boldsymbol{\delta }}_i} = \lambda _i^{\rm{T}}{\mathit{\boldsymbol{Q}}_b}{\lambda _i} $ | (16) |
4) 计算拟合模型参数的总体最小二乘估值:
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat x}}}_{i + 1}} = \left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\left( {\mathit{\boldsymbol{Q}} + {{\left. {\left( {\mathit{\boldsymbol{\hat x}}_i^{\rm{T}}{\mathit{\boldsymbol{Q}}_0}{{\mathit{\boldsymbol{\hat x}}}_i}} \right){\mathit{\boldsymbol{Q}}_b}} \right)}^{ - 1}}\mathit{\boldsymbol{B}} + {\mathit{\boldsymbol{G}}_i}\mathit{\boldsymbol{G}}_i^{\rm{T}} - } \right.} \right.}\\ {{{\left. {{\delta _i}{\mathit{\boldsymbol{Q}}_0}} \right)}^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}{{\left( {\mathit{\boldsymbol{Q}} + \left( {\mathit{\boldsymbol{\hat x}}_i^{\rm{T}}{\mathit{\boldsymbol{Q}}_0}{{\mathit{\boldsymbol{\hat x}}}_i}} \right){\mathit{\boldsymbol{Q}}_b}} \right)}^{ - 1}}\mathit{\boldsymbol{l}}} \end{array} $ | (17) |
应用步骤3)、4)进行迭代计算,直到参数估值收敛。本文应用约束矩阵克服病态法矩阵对参数估值的扰动性影响,避免了通过单一正则化参数实现病态EIV模型正则化算法存在的缺陷。
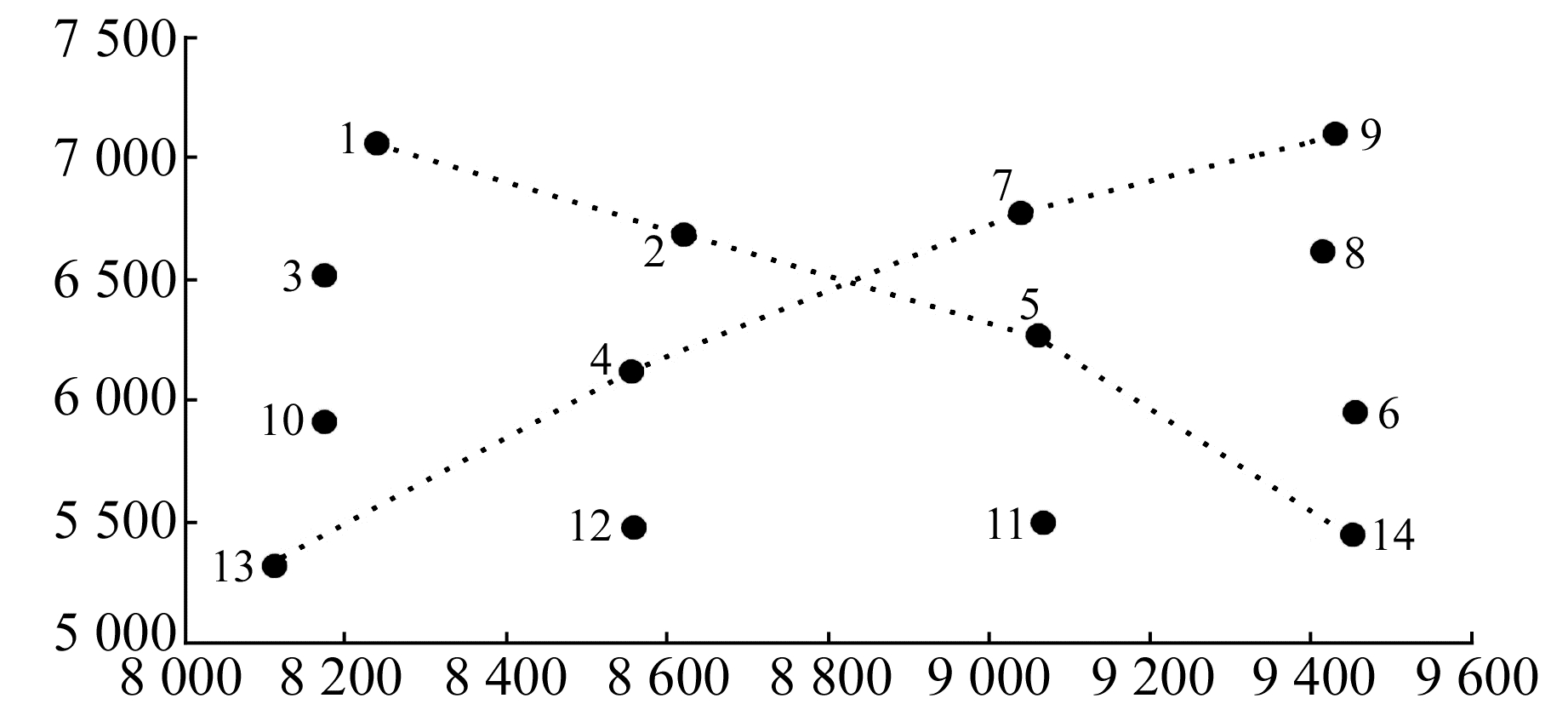
3 算例与分析应用某测区进行高程异常拟合实验。控制点高程(h)通过三等高程控制测量获得,控制点平面坐标(x, y)与大地高(H)通过布测GNSS C级控制网,并进行三维无约束平差获得。实验数据列于表 1,控制点点位分布如图 1,高程异常δ的近似取值为δ=H-h。
|
|
表 1 实验数据/m Tab. 1 Experimental data |
|
图 1 控制点点位分布 Fig. 1 Distribution of control points |
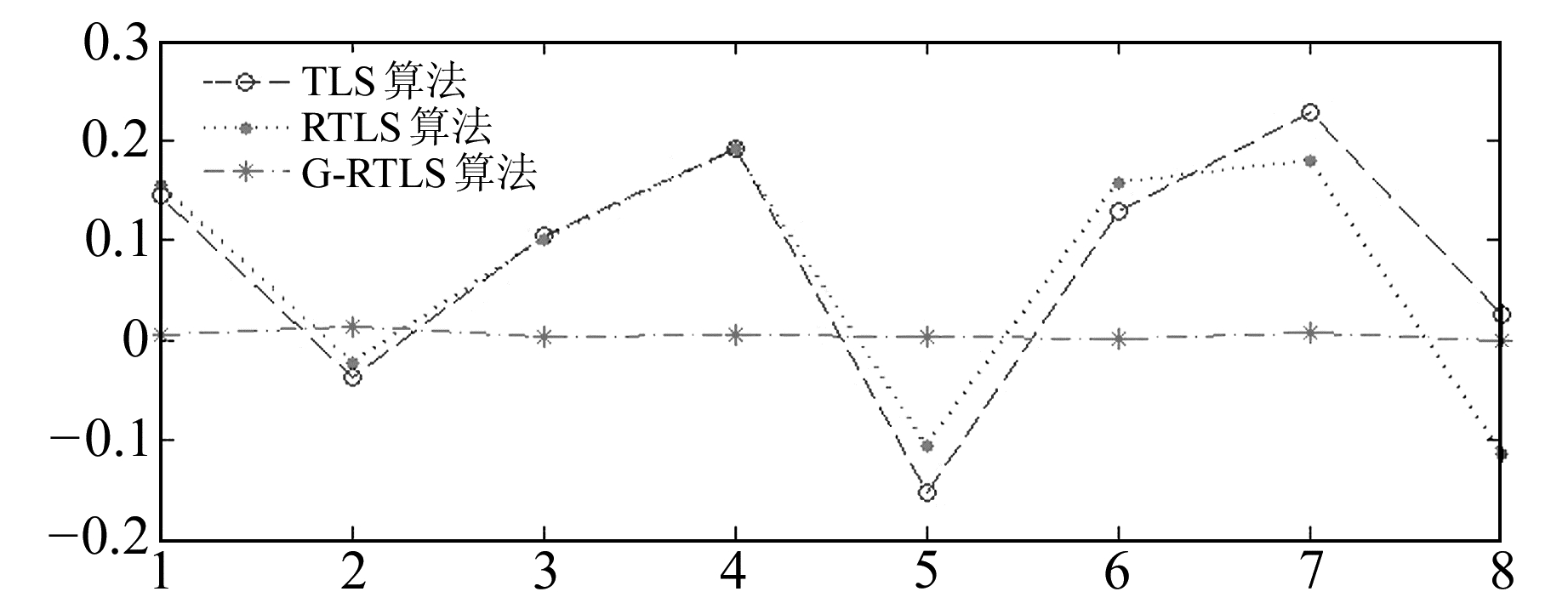
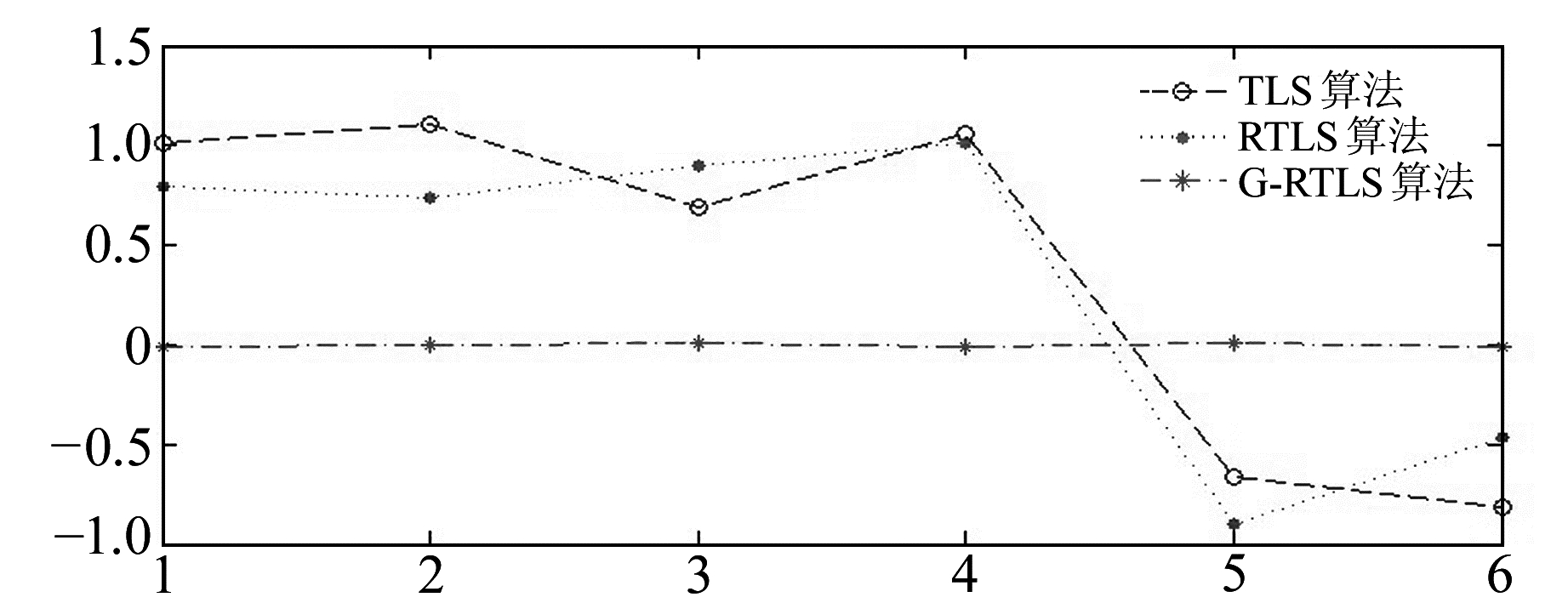
根据控制点1、2、4、5、7、9、13、14与式(2)建立观测方程,分别应用总体最小二乘算法(TLS)、基于岭估计的总体最小二乘算法(RTLS)、本文建立的广义岭估计算法(G-RTLS)求解高程异常拟合模型参数,并由其余控制点对拟合的外符合精度进行检核。由观测方程得到法方程矩阵的条件数约为3.06×1022,模型病态。由不同算法得到的拟合残差分别列于表 2、3,残差分布如图 2、3所示。
|
|
表 2 不同算法求解的内符合精度/m Tab. 2 Internal precision of control points based on different algorithms |
|
|
表 3 不同算法求解的外符合精度/m Tab. 3 External precision of control points based on different algorithms |
|
图 2 拟合点的残差分布 Fig. 2 Distribution of fitting points residual |
|
图 3 检核点的残差分布 Fig. 3 Distribution of check points residual |
实验表明,应用本文建立的算法实现高程异常拟合模型的正则化,拟合的内符合精度与外符合精度均优于总体最小二乘算法与基于岭估计的总体最小二乘算法,拟合的残差分布稳定。实验结果同时表明,在此算例中,相比于总体最小二乘算法,应用基于岭估计的总体最小二乘算法实现高程异常模型的正则化,并没有得到较好的拟合精度,其拟合精度与总体最小二乘算法相当。算例结果同时验证了文献[15]的研究结论。
4 结语以二次多项式模型为例讨论高程异常拟合病态EIV模型的正则化问题。在对总体最小二乘算法性质进行分析的基础上,为克服传统的基于岭估计算法的缺陷,应用法方程矩阵最小特征值对应的特征向量构建正则化矩阵,改进依靠单一参数既要实现模型的正则化、又要具有降正则化的缺陷。应用拉格朗日极值函数,建立病态EIV模型正则化的迭代算法。通过实测数据对所建立的算法进行验证,并与总体最小二乘算法和基于岭估计的总体最小二乘算法进行比较。实验结果表明,本文所建立的算法拟合精度优于其他两种算法。
| [1] |
Schaffrin B, Wieser A. On Weighted Total Least-Squares Adjustment for Linear Regression[J]. Journal of Geodesy, 2008, 82(7): 415-421 DOI:10.1007/s00190-007-0190-9
(  0) 0) |
| [2] |
Shen Yunzhong, Li Bofeng, Chen Yi. An Iterative Solution of Weighted Total Least-Squares Adjustment[J]. Journal of Geodesy, 2011, 85(4): 229-238 DOI:10.1007/s00190-010-0431-1
(  0) 0) |
| [3] |
陈义, 陆珏. 以三维坐标转换为例解算稳健总体最小二乘方法[J]. 测绘学报, 2012, 41(5): 715-722 (Chen Yi, Lu Jue. Performing 3D Similarity Transformation by Robust Total Least Squares[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 715-722)
(  0) 0) |
| [4] |
Mahboub V. On Weighted Total Least-squares for Geodetic Transformations[J]. Journal of Geodesy, 2012, 86(5): 359-367 DOI:10.1007/s00190-011-0524-5
(  0) 0) |
| [5] |
Fang X. Weighted Total Least-Squares with Constraints: A Universal Formula for Geodetic Symmetrical Transformations[J]. Journal of Geodesy, 2015, 89(5): 459-469 DOI:10.1007/s00190-015-0790-8
(  0) 0) |
| [6] |
陶叶青, 高井祥, 姚一飞. 基于中位数法的抗差总体最小二乘估计[J]. 测绘学报, 2016, 45(3): 297-301 (Tao Yeqing, Gao Jingxiang, Yao Yifei. Solution for Robust Total Least Squares Estimation Based on Median Method[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 297-301 DOI:10.11947/j.AGCS.2016.20150234)
(  0) 0) |
| [7] |
葛旭明, 伍吉仓. 病态总体最小二乘问题的广义正则化[J]. 测绘学报, 2012, 41(3): 372-377 (Ge Xuming, Wu Jicang. Generalized Regularization to Ill-Posed Total Least Squares Problem[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 372-377)
(  0) 0) |
| [8] |
Mahboub V, Sharifi M A. On Weighted Total Least-Squares with Linear and Quadratic Constraints[J]. Journal of Geodesy, 2013, 87(3): 279-286 DOI:10.1007/s00190-012-0598-8
(  0) 0) |
| [9] |
Zhang Songlin, Tong Xiaohua, Zhang Kun. A Solution to EIV Model with Inequality Constraints and Its Geodetic Applications[J]. Journal of Geodesy, 2013, 87(1): 23-28 DOI:10.1007/s00190-012-0575-2
(  0) 0) |
| [10] |
袁振超, 沈云中, 周泽波. 病态总体最小二乘模型的正则化算法[J]. 大地测量与地球动力学, 2009, 29(2): 131-134 (Yuan Zhenchao, Shen Yunzhong, Zhou Zebo. Regularized Total Least-Squares Solution to Ill-Posed Error-in-Variable Model[J]. Journal of Geodesy and Geodynamics, 2009, 29(2): 131-134)
(  0) 0) |
| [11] |
王乐洋, 于冬冬. 病态总体最小二乘问题的虚拟观测解法[J]. 测绘学报, 2014, 43(6): 575-581 (Wang Leyang, Yu Dongdong. Virtual Observation Method to Ill-Posed Total Least Squares Problem[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(6): 575-581)
(  0) 0) |
| [12] |
鲁铁定. 总体最小二乘平差理论及其在测绘数据处理中的应用[D]. 武汉: 武汉大学, 2010 (Lu Tieding. Research on the Total Least Squares and Its Application in Surveying Data Processing[D]. Wuhan: Wuhan University, 2010) http://kns.cnki.net/KCMS/detail/detail.aspx?filename=chxb201304028&dbname=CJFD&dbcode=CJFQ
(  0) 0) |
| [13] |
欧吉坤. 测量平差中不适定问题解的统一表达与选权拟合法[J]. 测绘学报, 2004, 33(4): 283-288 (Ou Jikun. Uniform Expression of Solutions of Ill-Posed Problems in Surveying Adjustment and the Fitting Method by Selection of the Parameter Weights[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(4): 283-288)
(  0) 0) |
| [14] |
林东方, 朱建军, 宋迎春, 等. 正则化的奇异值分解参数构造法[J]. 测绘学报, 2016, 45(8): 883-889 (Lin Dongfang, Zhu Jianjun, Song Yingchun, et al. Construction Method of Regularization by Singular Value Decomposition of Design Marix[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(8): 883-889 DOI:10.11947/j.AGCS.2016.20150134)
(  0) 0) |
| [15] |
Golub G H, Hansen P C, O'Leary D P. Tikhonov Regularization and Total Least Squares[J]. SIAM Journal on Matrix Analysis and Applications, 1999, 21(1): 185-194 DOI:10.1137/S0895479897326432
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38

