2. 湖南第一师范学院信息科学与工程学院,长沙市枫林三路1015号,410205
在载波相位测量中,周跳的探测和修复是数据预处理的重要内容。三频观测数据的出现,为周跳处理提供了更多波长更长、组合噪声更小、电离层延迟更小的优良组合观测值[1-2],利用观测值的组合特性,可以有效提高周跳探测的精度。常用的三频周跳探测方法主要有伪距相位组合法和无几何相位法。一般情况下,历元间的电离层误差可以忽略[3-4],但在电离层活跃期尤其是磁暴发生时,会导致电离层TEC显著变化[5-7],从而更加容易产生周跳误探。文献[8-9]研究了伪距/相位组合法探测周跳,文献[10]利用无几何相位组合法进行周跳探测与修复,文献[11]采用预先估计电离层延迟的方法探测电离层活跃期的周跳,文献[12]提出联合MW组合和电离层电子含量变化率(TECR)进行周跳探测与修复的方法。
本文基于传统的伪距相位组合以及无电离层组合,在此基础上联合TECR周跳探测方法,提出顾及电离层延迟影响的三频周跳探测与修复方法,并利用电离层活跃期三频数据进行周跳探测实验,得出相应的结论。
1 周跳探测与修复理论 1.1 三频无几何无电离层伪距相位组合探测周跳根据三频伪距相位组合理论[4],可得伪距相位组合模糊度为
| $ \begin{array}{*{20}{c}} {N = a{N_1} + b{N_2} + c{N_3} = }\\ {a{\varphi _1} + b{\varphi _2} + c{\varphi _3} - \left( {i{P_1} + j{P_2} + k{P_3}} \right)/{\lambda _w}} \end{array} $ | (1) |
式中,N为组合模糊度,λw为波长;a、b、c∈Z为载波相位组合系数,i、j、k∈R为伪距组合系数。
忽略历元间相位和伪距多径延迟变化项,历元间电离层延迟变化相对于波长可忽略不计。对式(1)进行历元间差分,可得三频无几何无电离层组合的周跳检测量表达式为:
| $ \begin{array}{*{20}{c}} {D = a\Delta {\varphi _1} + b\Delta {\varphi _2} + c\Delta {\varphi _3} - }\\ {\frac{{i\Delta {P_1} + j\Delta {P_2} + k\Delta {P_3}}}{{{\lambda _w}}}} \end{array} $ | (2) |
假设载波相位观测噪声标准差σφ=0.01周,伪距噪声σP=0.3 m,则由误差传播定律可得码相组合的周跳检验量标准差为:
| $ \begin{array}{*{20}{c}} {{\sigma _{\Delta N}} = }\\ {\sqrt {2\left[ {\left( {{a^2} + {b^2} + {c^2}} \right)\sigma _\varphi ^2 + \left( {{i^2} + {j^2} + {k^2}} \right)\sigma _P^2/\lambda _w^2} \right]} } \end{array} $ | (3) |
通常以3σΔN(置信水平为99.7%)为探测阈值,满足以下不等式即认为发生周跳:
| $ D > 3{\sigma _{\Delta N}} $ | (4) |
根据三频无几何无电离层伪距/相位组合系数优选结论[5]可知,除超宽巷组合(0, 1, -1)外,其他组合的阈值均接近于1周,只能探测2周及以上的周跳值,这主要是因为其组合受伪距观测噪声影响。因此,本文只选择(0, 1, -1)作为第一个周跳检验量。由于载波相位组合受观测噪声影响较小,引入三频相位无几何组合作为第二、三周跳检验量,但由于相位组合未能完全消除一阶电离层影响,在电离层活跃期其受电离层延迟影响严重,需对其进行进一步处理。
1.2 联合相位无几何和TECR法构造三频相位无几何组合方程如下:
| $ \left\{ \begin{array}{l} \mathit{\Phi } = a{\lambda _1}{\varphi _1} + b{\lambda _2}{\varphi _2} + c{\lambda _3}{\varphi _3}\\ a + b + c = 0 \end{array} \right. $ | (5) |
式中,Φ表示以m为单位的无几何载波相位组合观测值;λi表示第i频点的载波相位波长(i=1, 2, 3);φi表示第i频点的载波相位观测值(i=1, 2, 3);a、b、c为载波相位组合观测值组合系数。
顾及电离层残差,对载波相位组合观测方程进行历元间差分,可得:
| $ \begin{array}{*{20}{c}} {\Delta \mathit{\Phi } = a{\lambda _1}\Delta {\varphi _1} + b{\lambda _2}\Delta {\varphi _2} + c{\lambda _3}\Delta {\varphi _3} = }\\ \eta \Delta {I}'+a{{\lambda }_{1}}\Delta {{N}_{1}}+b{{\lambda }_{2}}\Delta {{N}_{2}}+c{{\lambda }_{3}}\Delta {{N}_{3}} \end{array} $ | (6) |
| $ \eta = a{\lambda _1} + b{\lambda _2}{f_1}/{f_2} + c{\lambda _3}{f_1}/{f_3} $ | (7) |
式中,η为以周为单位的电离层残差变化系数,I′为f1上以周为单位的电离层延迟,其他同式(5)。
对式(6)进行变换可得周跳检验量Da, b, c:
| $ \begin{array}{*{20}{c}} {D = {\lambda _1}\Delta {N_1} + b{\lambda _2}\Delta {N_2} + c{\lambda _3}\Delta {N_3} = }\\ {a{\lambda _1}\Delta {\varphi _1} + b{\lambda _2}\Delta {\varphi _2} + c{\lambda _3}\Delta {\varphi _3} - \eta \Delta I'} \end{array} $ | (8) |
若无周跳发生,式(8)的值应该在零附近波动,根据误差传播定律得周跳检测量的误差为:
| $ {\sigma _D} = \sqrt 2 \cdot \sqrt {{a^2}\lambda _1^2 + {b^2}\lambda _2^2 + {c^2}\lambda _3^2} \cdot {\sigma _\varphi } $ | (9) |
在电离层平静期,可忽略电离层残差的影响。若D≥NσD,N为倍增因子,N取3表示99.7%的置信水平,N取4表示99.9%的置信水平,若此不等式成立说明该历元发生周跳。
对于无几何相位组合系数的选择,要尽可能地削弱电离层的影响,同时周跳检验量的误差也要尽可能低。根据无几何相位组合观测值理论[5],本文选择(1, -1, 0)和(1, 0, -1)两组无几何相位组合进行周跳探测。
在电离层活跃期,由于无几何相位组合残差含有一阶电离层残差,当电离层电子含量变化较大时,周跳检验量的误差也会随之增大,此时采用传统无几何相位组合探测周跳会出现误探现象。为解决电离层残差带来的影响,本文通过TECR法来探测是否发生周跳。
第k历元的相位组合表达式如下:
| $ \begin{array}{*{20}{c}} {\mathit{\Phi }\left( k \right) = a{\lambda _1}{\varphi _1} + b{\lambda _2}{\varphi _2} + c{\lambda _3}{\varphi _3} = }\\ {\eta I + a{\lambda _1}{N_1} + b{\lambda _2}{N_2} + c{\lambda _3}{N_3} + {\varepsilon _\varphi }} \end{array} $ | (10) |
| $ \eta = a + bf_1^2/f_2^2 + cf_1^2/f_3^2 $ | (11) |
式中,η为以m为单位的电离层放大系数,I为f1上以m为单位的电离层延迟。由式(10)可得无几何载波相位观测量第k个历元的电离层总电子含量(TEC)表达式如下:
| $ \begin{array}{*{20}{c}} {{\rm{TE}}{{\rm{C}}_\varphi }\left( k \right) = - \left[ {\mathit{\Phi }\left( k \right) + \left( {a{\lambda _1}{N_1} + b{\lambda _2}{N_2} + } \right.} \right.}\\ {\left. {\left. {c{\lambda _3}{N_3} + {\varepsilon _\varphi }} \right)} \right]/\left( {40.3\eta \times {{10}^{16}}} \right)} \end{array} $ | (12) |
假设历元间隔为Δt,对上式进行历元间作差得第k个历元的电子含量变化率TECRφ(k):
| $ \begin{array}{*{20}{c}} {{\rm{TEC}}{{\rm{R}}_\varphi }\left( k \right) = \frac{{\left[ {{\rm{TE}}{{\rm{C}}_\varphi }\left( k \right) - {\rm{TE}}{{\rm{C}}_\varphi }\left( {k - 1} \right)} \right]}}{{\Delta t}} = - }\\ {\frac{{\mathit{\Phi }\left( k \right) - \mathit{\Phi }\left( {k - 1} \right) + \left( {a{\lambda _1}\Delta {N_1} + b{\lambda _2}\Delta {N_2} + c{\lambda _3}\Delta {N_3}} \right)}}{{40.3\eta \times {{10}^{16}}\Delta t}}} \end{array} $ | (13) |
将式(13)代入式(8)可得第i历元的周跳检验量:
| $ \begin{array}{*{20}{c}} {D = a{\lambda _1}\Delta {N_1} + b{\lambda _2}\Delta {N_2} + c{\lambda _3}\Delta {N_3} = - }\\ {\left( {\mathit{\Phi }\left( k \right) - \mathit{\Phi }\left( {k - 1} \right)} \right) - 40.28\eta \times {{10}^{16}}\Delta t \cdot {\rm{TEC}}{{\rm{R}}_\varphi }\left( k \right)} \end{array} $ | (14) |
周跳检验量的方差为:
| $ \begin{array}{*{20}{c}} {{\sigma ^2}\left( k \right) = {{\left( {40.3 \times {{10}^{16}}\Delta t \cdot \eta \cdot {\rm{TEC}}{{\rm{R}}_\varphi }\left( k \right)} \right)}^2} \cdot }\\ {\sigma _{{\rm{TEC}}{{\rm{R}}_\varphi }\left( k \right)}^2 + 2\left( {{a^2}\lambda _1^2 + {b^2}\lambda _2^2 + {c^2}\lambda _3^2} \right)\sigma _\varphi ^2 = }\\ {12\left( {{a^2}\lambda _1^2 + {b^2}\lambda _2^2 + {c^2}\lambda _3^2} \right)\sigma _\varphi ^2} \end{array} $ | (15) |
式中,σφ为载波相位观测值标准差,一般为mm级。假设σφ=5 mm,通过以上分析可知,基于TECRφ的周跳检验量可以达到很高的精度,其标准差可以达到mm级。值得一提的是,该方法中,所有分析的前提都是基于短时间内(通常不超过30 s)电离层变化率TECRφ(k)为常量进行的。
对第k历元的观测值进行周跳探测时,假设历元k之前的所有历元观测值没有周跳或者周跳已经被修复,此时可通过第k-1和k-2个历元的TECR值来估计当前历元的TECRφ(k):
| $ \begin{array}{*{20}{c}} {{\rm{TEC}}{{\rm{R}}_\varphi }\left( k \right) = }\\ {{\rm{TEC}}{{\rm{R}}_\varphi }\left( {k - 1} \right) + {\rm{TEC}}{{{\rm{R'}}}_\varphi }\left( {k - 1} \right) \cdot \Delta t} \end{array} $ | (16) |
| $ \begin{array}{*{20}{c}} {{\rm{TEC}}{{{\rm{R'}}}_\varphi }\left( k \right) = }\\ {\frac{{{\rm{TEC}}{{\rm{R}}_\varphi }\left( {k - 1} \right) + {\rm{TEC}}{{\rm{R}}_\varphi }\left( {k - 2} \right)}}{{\Delta t}}} \end{array} $ | (17) |
将式(13)计算的TECR值和式(16)估计的TECR值的差值称为TECR残差。如果该残差超过给定的阈值(一般取0.15 TECu/s),则认为第k个历元发生了周跳。
1.3 周跳探测、修复与确认根据本文选择的3个线性无关的伪距相位组合和无几何相位组合进行周跳探测与修复,联立方程组如下:
| $ \mathit{\boldsymbol{B}}\Delta \mathit{\boldsymbol{N = }}\left[ {\begin{array}{*{20}{c}} 0&1&{ - 1}\\ {{\lambda _1}}&{ - {\lambda _2}}&0\\ {{\lambda _1}}&0&{ - {\lambda _3}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta {N_1}}\\ {\Delta {N_2}}\\ {\Delta {N_3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{l_1}}\\ {{l_2}}\\ {{l_3}} \end{array}} \right] = \mathit{\boldsymbol{L}} $ | (18) |
式中,ΔNi和li分别为第i频点的周跳值和相应的周跳探测变化量。利用方程组的线性无关性,可以直接求解ΔN1、ΔN2和ΔN3的浮点值,但由于(BTB)-1的条件数较大,L取值的微小变动将导致解产生较大的变化。为保证周跳修复的准确性,本文采用1-范数最小原则[10]进行周跳修复的搜索确认,衡量准则如下:
| $ {\left\| {\mathit{\boldsymbol{B}}\Delta \mathit{\boldsymbol{N}} - \mathit{\boldsymbol{L}}} \right\|_1} = \min $ | (19) |
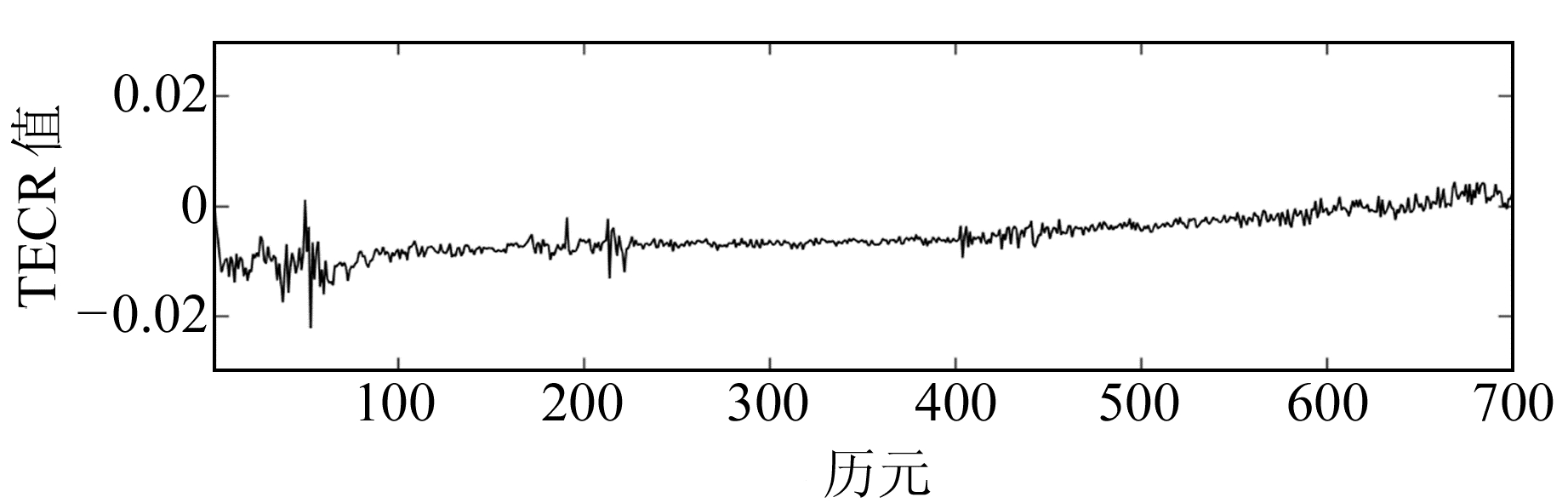
为研究电离层平静期的电子含量变化率,采用2016-06-08站点jfng的观测数据(30 s采样间隔)解算TECRφ,结果如图 1所示。由图 1可知,当天电离层变化较为平静,TECRφ变化很小,绝对值几乎小于0.02 TECu/s。
|
图 1 平静期电离层总电子含量变化率 Fig. 1 TECR in ionosphere quiet phase |
为研究电离层活跃期电子含量变化率,采用2013-03-17的IGS跟踪站cut0的数据。当天发生了磁暴,赤道、中纬度地区以及极光区上空TEC变化显著。计算当天的TECRφ(k)变化如图 2所示,由于原始观测数据无周跳,为了验证TECR探测周跳效果,在利用TECR残差法进行周跳探测时,依次在每隔50历元处分别加入不同组合的周跳,其组合分别为(0, 0, 1)、(0, 1, 1)、(1, 1, 1)、(1, 1, 2)、(1, 2, 1)、(1, 2, 2)、(2, 0, 0)、(2, 0, 1)、(2, 0, 2)、(2, 1, 0)、(1, 1, 0)、(2, 1, 2)、(2, 2, 0)、(2, 2, 1)、(2, 2, 2)、(13, 10, 2)、(4, 2, 2)。

|
图 2 活跃期电离层总电子含量变化率 Fig. 2 TECR in ionosphere activity phase |
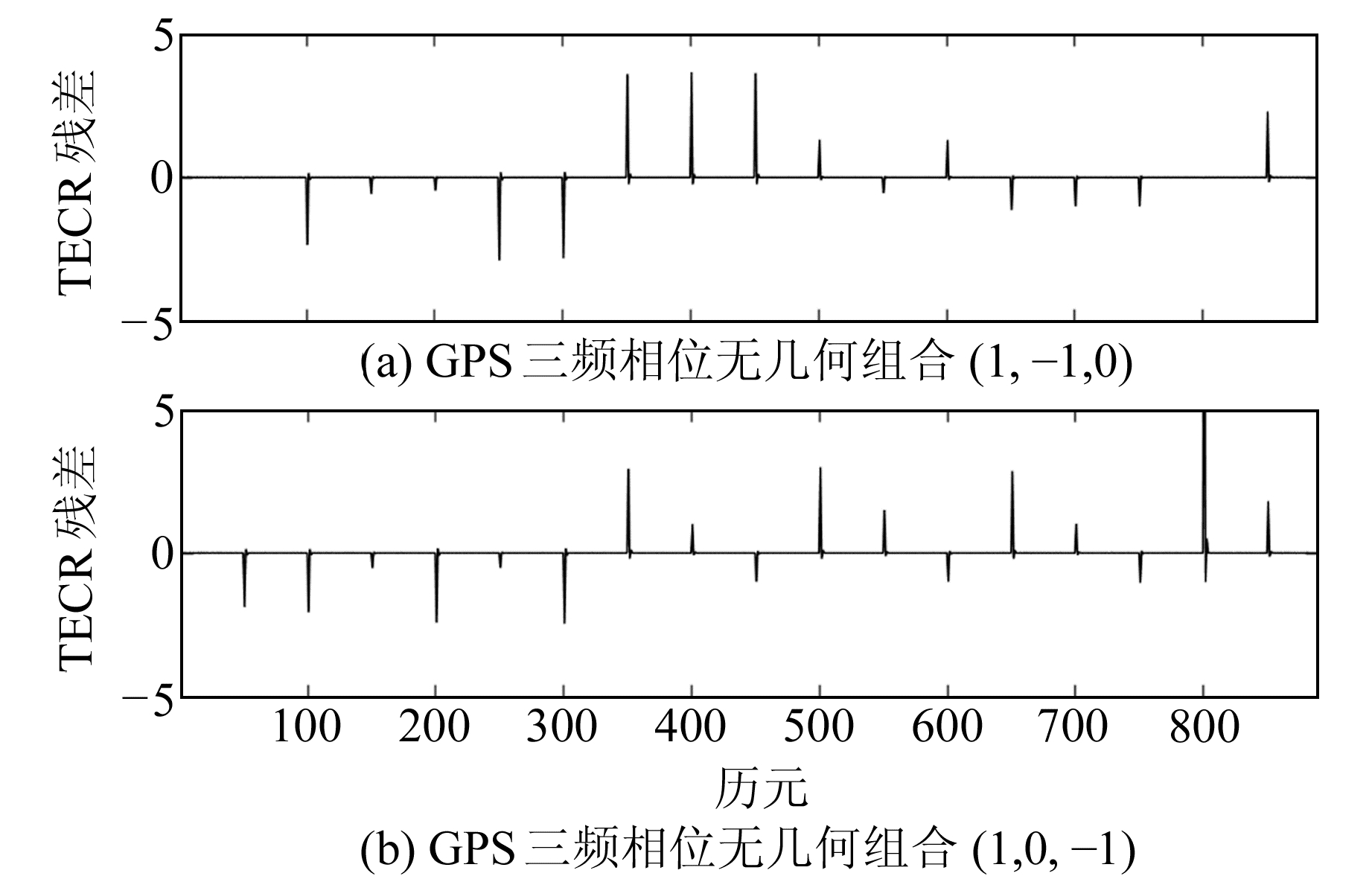
如图 2所示,当磁暴发生时,电离层的电子含量不再保持稳定,而是呈上升趋势,从而导致电离层延迟增大。图 3给出(1, -1, 0)和(1, 0, -1)无几何相位组合的周跳探测结果,由图可知,电离层变化剧烈期间,传统的无几何周跳检验量明显受到电离层延迟影响,其探测值低于实际周跳值,从而产生误探。因此要准确探测与修复周跳,必须削弱电离层的影响。

|
图 3 电离层活跃期无几何相位组合周跳检验量 Fig. 3 The detection value of geometry-free phase combination in ionospheric activity phase |
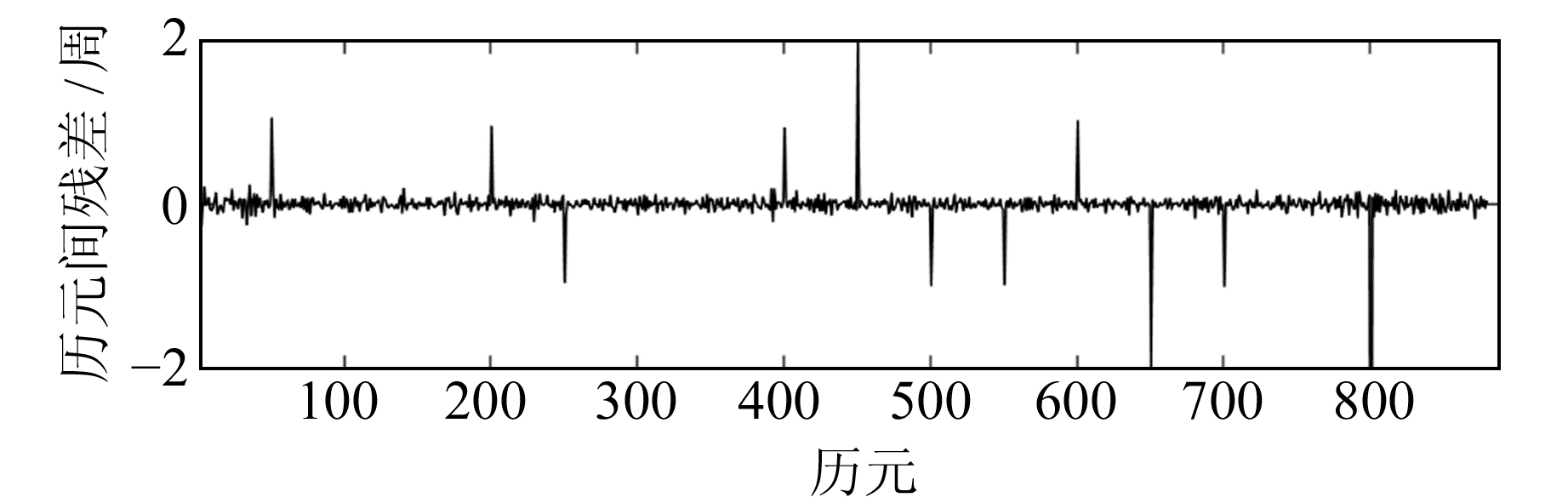
图 4给出采用(1, -1, 0)和(1, 0, -1)无几何相位组合时,TECR残差法探测周跳的效果。除了λ1ΔN1=λ2ΔN2和λ1ΔN1=λ3ΔN3的不敏感周跳外,其他组合的TECR残差均明显超过阈值。因此,采用TECR法可以准确探测除敏感周跳以外的所有周跳组合。对于无几何相位组合的敏感周跳,以(1, -1, 0)为例,人为添加(13, 10, 2)敏感周跳进行探测。由图可知,尽管(1, -1, 0)无法有效探测到(13, 10, 2)周跳值,但其可以被伪距相位组合以及(1, 0, -1)无几何相位组合探测到。
|
图 4 电离层活跃期TECR残差值 Fig. 4 Residual of TECR in ionospheric activity phase |
图 5给出伪距相位组合(0, 1, -1)在电离层活跃期的周跳探测效果。由图可知,此组合并不受电离层活动的影响,可以准确探测出除ΔN2=ΔN3敏感周跳以外的所有周跳,这是因为超宽巷组合的波长达到了5.86 m,远远大于电离层活动造成的误差,因此可以忽略电离层的影响。对于其敏感周跳,由图 4可知,其敏感周跳组合均可被相位无几何组合探测到。
|
图 5 无几何无电离层伪距相位组合周跳检验量 Fig. 5 The detection value of the geometry-free and ionosphere-free code-phase combinations |
图 6给出(1, -1, 0)和(1, 0, -1)无几何相位+TECR法的周跳探测量。由图可知,即使在电离层活跃期,本文提出的方法依然可以准确探测出除敏感周跳以外的所有周跳组合,然后根据图示的周跳探测变化值可以有效地修复周跳值。

|
图 6 活跃期无几何相位组合+TECR法周跳检验量 Fig. 6 The detection value of the geometry-free phase combinations based on TECR |
由图 4和图 5可知,尽管伪距相位组合和无几何相位组合均有敏感周跳,但任何一个组合的敏感周跳均可被其他至少一个组合探测到,这3个组合可以探测到人为添加的所有周跳组合。
3 结语GPS无几何无电离层伪距相位组合法能保证整周模糊度的整数特性,但只有(0, 1, -1)能实现对小周跳的探测;GPS无几何相位历元间电离层延迟小,且不受伪距噪声影响,但不能保证整周模糊度的整数特性,且在电离层活跃期受电离层影响较大,从而出现周跳误探。将其与TECR方法结合,可以减小电离层的影响,实现对小周跳的探测。本文以无几何无电离层码相组合为第1检验量,以2个基于TECR的无几何相位组合作为第2、3检验量,联合构成3个线性无关周跳检验量,实现在电离层活跃期对任意周跳组合的实时探测。为确保正确修复,本文采用搜索法实时修复周跳,适用于精密单点定位的数据预处理。
| [1] |
熊伟, 伍岳, 孙振冰, 等. 多频数据组合在周跳探测和修复上的应用[J]. 武汉大学学报:信息科学版, 2007, 32(4): 319-322 (Xiong Wei, Wu Yue, Sun Zhenbing, et al. Application of Multi-Frequency Combination Observation in Cycle Slip Detection and Restoration[J]. Geomatics and Information Science of Wuhan University, 2007, 32(4): 319-322)
(  0) 0) |
| [2] |
王泽民, 刘景斌. 卫星定位系统相位组合观测值的模型研究[J]. 武汉大学学报:信息科学版, 2006, 28(6): 723-727 (Wang Zemin, Liu Jingbin. Model of Inter-Frequency Combinations of Galileo GNSS[J]. Geomatics and Information Science of Wuhan University, 2006, 28(6): 723-727)
(  0) 0) |
| [3] |
刘旭春, 伍岳, 张正禄, 等. GPS三频数据在周跳和粗差探测与修复中的应用[J]. 煤炭学报, 2006, 31(5): 585-588 (Liu Xuchun, Wu Yue, Zhang Zhenglu, et al. Application of GPS Triple-Frequency Data in Detection and Repair of Cycle Slip and Gross Error[J]. Journal of China Coal Society, 2006, 31(5): 585-588)
(  0) 0) |
| [4] |
黄令勇, 翟国军, 欧阳永忠, 等. 三频GNSS电离层周跳处理[J]. 测绘学报, 2015, 44(7): 717-725 (Huang Lingyong, Zhai Guojun, Ouyang Yongzhong, et al. Ionospheric Cycle Slip Processing in Triple-Frequency GNSS[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 717-725 DOI:10.11947/j.AGCS.2015.20140348)
(  0) 0) |
| [5] |
黄令勇, 翟国军, 欧阳永忠, 等. 削弱电离层影响的三频TurboEdit周跳处理方法[J]. 测绘学报, 2015, 44(8): 840-847 (Huang Lingyong, Zhai Guojun, Ouyang Yongzhong, et al. Triple-Frequency TurboEdit Cycle-Slip Processing Method of Weakening Ionospheric Activity[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(8): 840-847 DOI:10.11947/j.AGCS.2015.20140380)
(  0) 0) |
| [6] |
郑作亚, 程宗颐, 黄珹, 等. 对Blewitt周跳探测与修复方法的改进[J]. 天文学报, 2005, 46(2): 216-224 (Zheng Zuoya, Cheng Zongyi, Huang Cheng, et al. Improving of Cycle-Slip Detection and Correction of Blewitt Method[J]. Acta Astronomica Sinca, 2005, 46(2): 216-224)
(  0) 0) |
| [7] |
Liu Z Z. A New Automated Cycle Slip Detection and Repair Method for a Single Dual-Frequency GPS Receiver[J]. Journal of Geodesy, 2010, 85(3): 171-183
(  0) 0) |
| [8] |
李金龙, 杨元喜, 徐君毅, 等. 基于伪距相位组合实时探测与修复GNSS三频非差观测数据周跳[J]. 测绘学报, 2011, 40(6): 717-722 (Li Jinlong, Yang Yuanxi, Xu Junyi, et al. Real-Time Cycle-Slip Detection and Repair Based on Code-Phase Combinations for GNSS Triple-Frequency Un-Differenced Observations[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 717-722)
(  0) 0) |
| [9] |
陈品馨, 章传银, 黄昆学. 用相位减伪距法和电离层残差法探测和修复周跳[J]. 大地测量与地球动力学, 2010, 30(2): 120-124 (Chen Pinxin, Zhang Chuanyin, Huang Kunxue. Cycle Slip Detecting and Repairing by Use of Phase Reduce Pseudorange Law and Ionized Layer Remnant Method of Difference[J]. Journal of Geodesy and Geodynamics, 2010, 30(2): 120-124)
(  0) 0) |
| [10] |
黄令勇, 宋力杰, 王琰, 等. 北斗三频无几何相位组合周跳探测与修复[J]. 测绘学报, 2012, 41(5): 763-768 (Huang Lingyong, Song Lijie, Wang Yan, et al. Beidou Triple-Frequency Geometry-Free Phase Combination for Cycle-Slip Detection and Correction[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 763-768)
(  0) 0) |
| [11] |
Banville S, Langley R B. Mitigationg the Impact of Ionospheric Cycle Slips in GNSS Observations[J]. Journal of Geodesy, 2013, 87(2): 179-193 DOI:10.1007/s00190-012-0604-1
(  0) 0) |
| [12] |
张顺, 姚宜斌, 陈鹏, 等. GPS非差数据周跳探测方法研究[J]. 大地测量与地球动力学, 2012, 32(1): 101-104 (Zhang Shun, Yao Yibin, Chen Peng, et al. Research on Cycle Slip Detection Methods for Un-Differenced GPS Data[J]. Journal of Geodesy and Geodynamics, 2012, 32(1): 101-104)
(  0) 0) |
2. School of Information Science and Engineering, Hunan First Normal College, 1015 Fenglinsan Road, Changsha 410205, China
 2018, Vol. 38
2018, Vol. 38


