2. 山东科技大学测绘科学与工程学院,青岛市前湾港路579号,266003
随着GPS观测技术的不断发展和完善,尤其是卫星星历精度的不断提高、地球极移以及卫星钟信息更新周期的不断缩短、全球IGS站数量的快速增加,使其定位精度有了很大提高,可以满足地壳形变和板块运动监测的需求[1]。区域GPS监测网通常由几十个甚至上百个CORS站组成,其坐标统一到全球框架中。在区域GPS网络中,不同站点时间序列中存在一种与时间空间关联的误差,即共模误差(common mode error, CME)[2]。通过空间滤波剔除共模误差,能够提高GPS站坐标时间序列的精度,对于改进形变模式分析具有重要的意义。
对于区域GPS坐标时间序列,目前剔除共模误差一般使用空间滤波,主要包括堆栈法(Stacking)、主分量分析法(PCA)和K-L(Karhunen-Loeve)变换空间滤波[3-4]。堆栈法假设共模误差在区域内的所有站点上具有空间均匀分布的特性,对几百km范围内的区域GPS网有很好的近似[5]。因此,本文对四川连续GPS基准站坐标时间序列进行去趋势项和去均值处理,获取坐标残差时间序列,然后使用堆栈法对坐标残差序列进行空间滤波,以提取共模误差。最后,使用CATS软件对滤波后的站坐标时间序列进行频谱特征以及噪声特性分析[6],并估计了不同噪声模型对测站速度的影响。
1 噪声模型及分析方法 1.1 噪声分类地球物理现象功率谱函数通常用1/fα来表示,GPS站坐标时间序列中的噪声也可以用一种幂律过程[7]来描述:
| $ {{P}_{x}}\left( f \right)={{P}_{0}}{{\left( f/{{f}_{0}} \right)}^{\kappa }} $ | (1) |
式中,Px(f)表示功率谱密度,f表示频率; P0、f0表示正态化常数; κ是谱指数,用来表示功率谱在双对数空间的斜率。在时域分析中,谱指数κ能够有效地判断噪声特性,当-3 < κ < -1时为非静态过程,称为分形布朗运动; 当-1 < κ < 1时为静态过程,称为分形高斯过程。其中,κ=-2时为随机漫步噪声,κ=-1时为闪烁噪声,κ=0时为白噪声。
1.2 极大似然估计法在GPS站坐标时间序列包含有色噪声的前提下,当前主要有两种常用的估计噪声特征的方法—极大似然估计法和功率谱估计法。本文主要使用极大似然估计法来确定最优噪声组合模型,并同时计算噪声的具体分量值。
为了估计噪声分量以及线性方程中的待求函数,对于给定的坐标序列残差
| $ \begin{gathered} {\text{lik}}\left( {\hat v, \mathit{\boldsymbol{C}}} \right) = \hfill \\ \frac{1}{{\left( {2\pi } \right)N/2\left( {\det \mathit{\boldsymbol{C}}} \right)1/2}}\exp \left( {-0.5{{\hat v}^{\text{T}}}{\mathit{\boldsymbol{C}}^{-1}}\hat v} \right) \hfill \\ \end{gathered} $ | (2) |
式中,C代表数据中假设噪声的协方差阵,det是一个矩阵行列式,N为历元数。lik值最大等价于lik值的对数达到最大:
| $ \begin{gathered} \ln \left[{{\text{lik}}\left( {\hat v, \mathit{\boldsymbol{C}}} \right)} \right] = - 0.5\left[{{\text{ln}}\left( {{\text{det}}\mathit{\boldsymbol{C}}} \right) + } \right. \hfill \\ \left. {\hat v{\mathit{\boldsymbol{C}}^{-1}}\hat v + N\ln \left( {2\pi } \right)} \right] \hfill \\ \end{gathered} $ | (3) |
这样就可以计算多种模型组合,求取基于不同模型的极大似然估计值,选择估值最大的噪声模型作为最优噪声组合[8-9]。
2 GPS站坐标时间序列的获取 2.1 数据处理本文使用GAMIT/GLOBK10.50对四川省23个连续GPS基准站在2010-01-01~06-12期间的观测数据进行处理。另外,为了将IGS站坐标和框架引入到基线处理中来,在解算过程中引入中国大陆及周边10个IGS站(BJFS、WUHN、LHAZ、AIRA、YSSK、SHAO、URUM、TIXI、TCMS、KIT3)同时段的数据。
使用GAMIT进行基线解算的策略如下:基线处理类型为松弛解(RELAX); 使用无电离层线性组合(LC_AUTCLN)观测值的选择类型; 截止高度角为10°; 对流层折射模型使用萨斯塔莫宁模型(Saastamoinen); 天顶延迟模型13个; 潮汐改正使用FES2004模型; 采用ITRF2008参考框架; 光压模型为BERNE模型; 使用J2000空间惯性参考系。将10个IGS站设置为固定站,地心纬度N、经度L松弛量设定为0.05 m,矢径R松弛量设定为0.10 m,将四川GPS站设置为非固定站,站坐标约束为9.999 m、9.999 m、9.999 m。
处理完基线之后,使用GLOBK将GAMIT基线解算的松驰解h文件在框架ITRF2008下进行区域网平差,调用globk、glorg模块进行解算,选用中国大陆及周边的10个IGS站作为框架稳定站。部分测站由于天线变动或地震等原因发生了阶跃,使用eq_rename文件对其进行改正。最后从约束平差结果org文件中获取四川GPS站点的坐标时间序列(图 1)。

|
图 1 SCMN站原始坐标时间序列 Fig. 1 Original coordinate time series of SCMN station |
在提取共模误差的过程中,需要使用区域网内各测站的残差时间序列。坐标残差时间序列由坐标时间序列剔除掉线性项和周期项得到,其公式如下:
| $ \begin{gathered} {v_i} = y\left( {{t_i}} \right)-a-b{t_i}-c\sin \left( {2\pi {t_i}} \right) - d\cos \left( {2\pi {t_i}} \right) - \hfill \\ e\sin \left( {4\pi {t_i}} \right) - f\cos \left( {4\pi {t_i}} \right) - \sum\limits_{j = 1}^{{n_g}} {{g_i}H\left( {{t_i} - {T_{gj}}} \right)} \hfill \\ \end{gathered} $ | (4) |
其中,vi为第i个历元的观测残差; y(ti)表示站坐标时间序列; ti代表以a为单位的解算历元; a表示测站初始坐标,b为线性速度,c、d表示年周期性运动系数,e、f表示半年周期性运动系数;
空间相关分析发现,在1 000 km之内,坐标序列具有较高的相关性。四川省南北最长跨度约为920 km,东西最长跨度约为1 040 km,空间相关性较高。因此,在获取测站坐标残差时间序列以后,本文使用堆栈法提取区域的共模误差。假设有一个m×n的矩阵X,其中m代表历元数,n代表区域网络中GPS测站数,X中的每一个元素为测站坐标的残差值。对于历元i=1, 2, …, m,区域中共模误差εi可用下式计算:
| $ {\varepsilon _i} = \frac{{\sum\limits_{j = 1}^n {\left( {x\left( {{t_i}, {s_j}} \right)\delta _{i, j}^2} \right)} }}{{\sum\limits_{j = 1}^s {\left( {1/\delta _{i, j}^2} \right)} }} $ | (5) |
式中,δi, k代表第i天第k个测站的中误差。这种方法实际上就是将各个历元每个测站的残差加权平均值作为该历元的共模误差(图 2)。
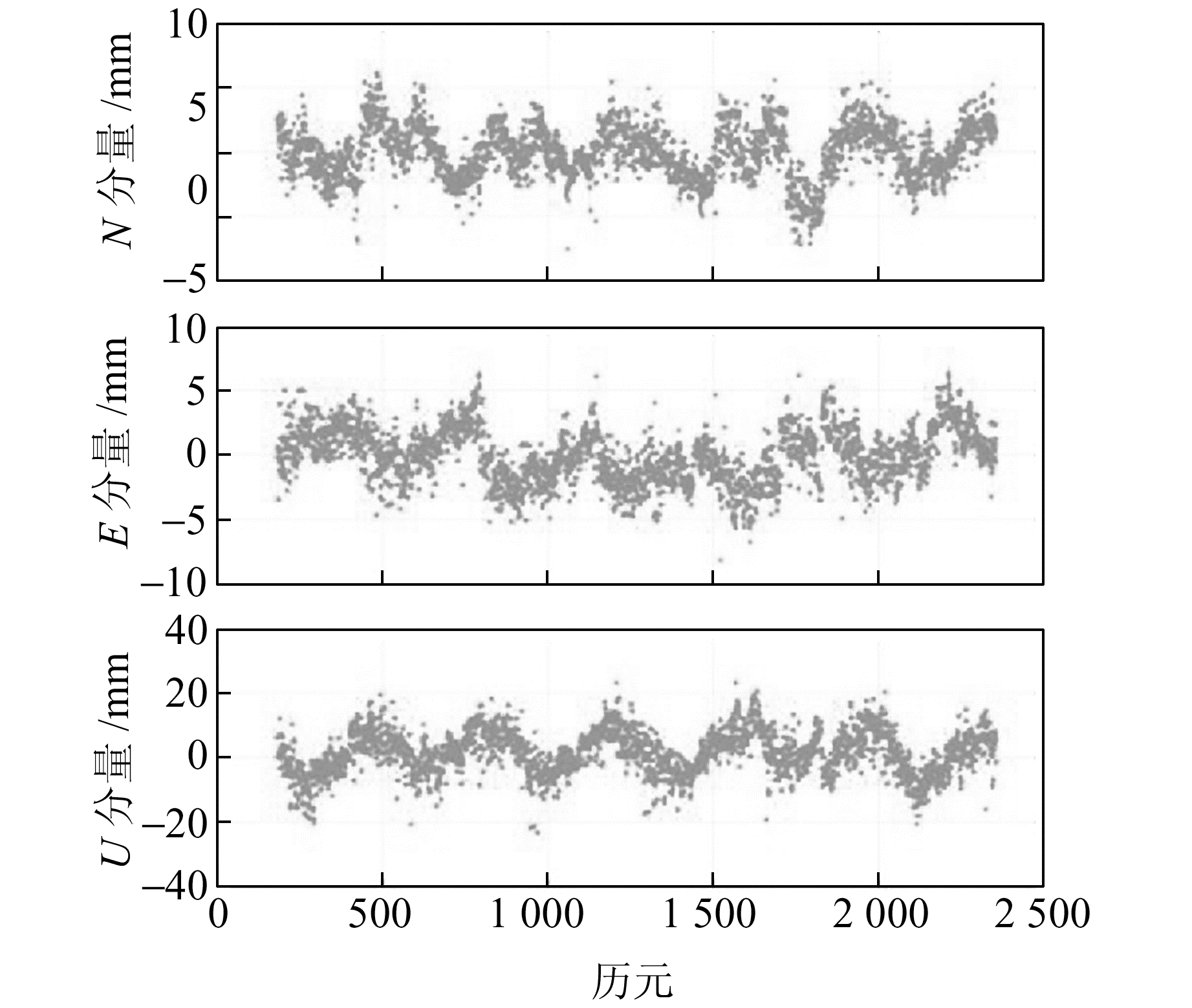
|
图 2 提取到的共模误差 Fig. 2 The common mode error |
起初,人们认为GPS站坐标时间序列中仅存在白噪声(WN)。随着对GPS站坐标时间序列研究的进一步深入,许多学者发现GPS站坐标时间序列中还存在着与时空相关的闪烁噪声(FN)和随机游走噪声(RWN)等有色噪声[11]。
通过谱指数计算可以分析时间序列中幂指数噪声的大概类型。本文通过CATS软件获取滤波后的四川连续GPS基准站时间序列的谱指数(见表 1,单位mm)。由表 1可见,四川区域网中23个基准站各坐标分量的噪声谱指数均介于-1~0之间,说明这些测站的噪声模型并非单一的噪声模型,而是包括白噪声在内的几种噪声模型的组合。
|
|
表 1 空间滤波后测站3个方向的谱指数值 Tab. 1 Spectral index values of the spatial filter in the three directions |
为估计四川连续GPS基准站的最佳噪声模型,根据上文分析,假设3种模型组合:白噪声+闪烁噪声(WN+FN); 白噪声+随机游走噪声(WN+RWN); 白噪声+闪烁噪声+随机游走噪声(WN+FN+RWN),使用CATS软件估计3种模型下的最大似然值,并与WN模型下的最大似然值作差,结果如图 3~5所示。
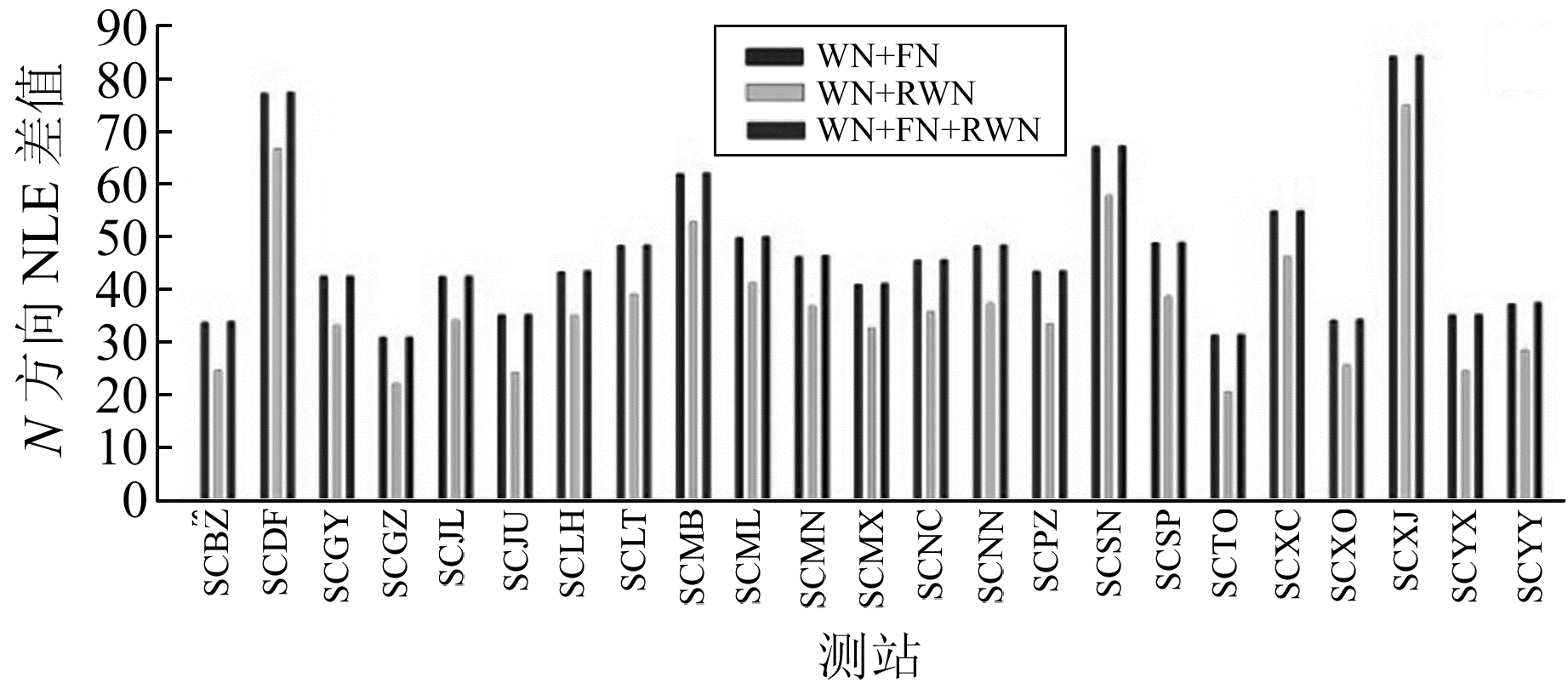
|
图 3 测站N方向最大似然差值 Fig. 3 Maximum likelihood difference of N direction |
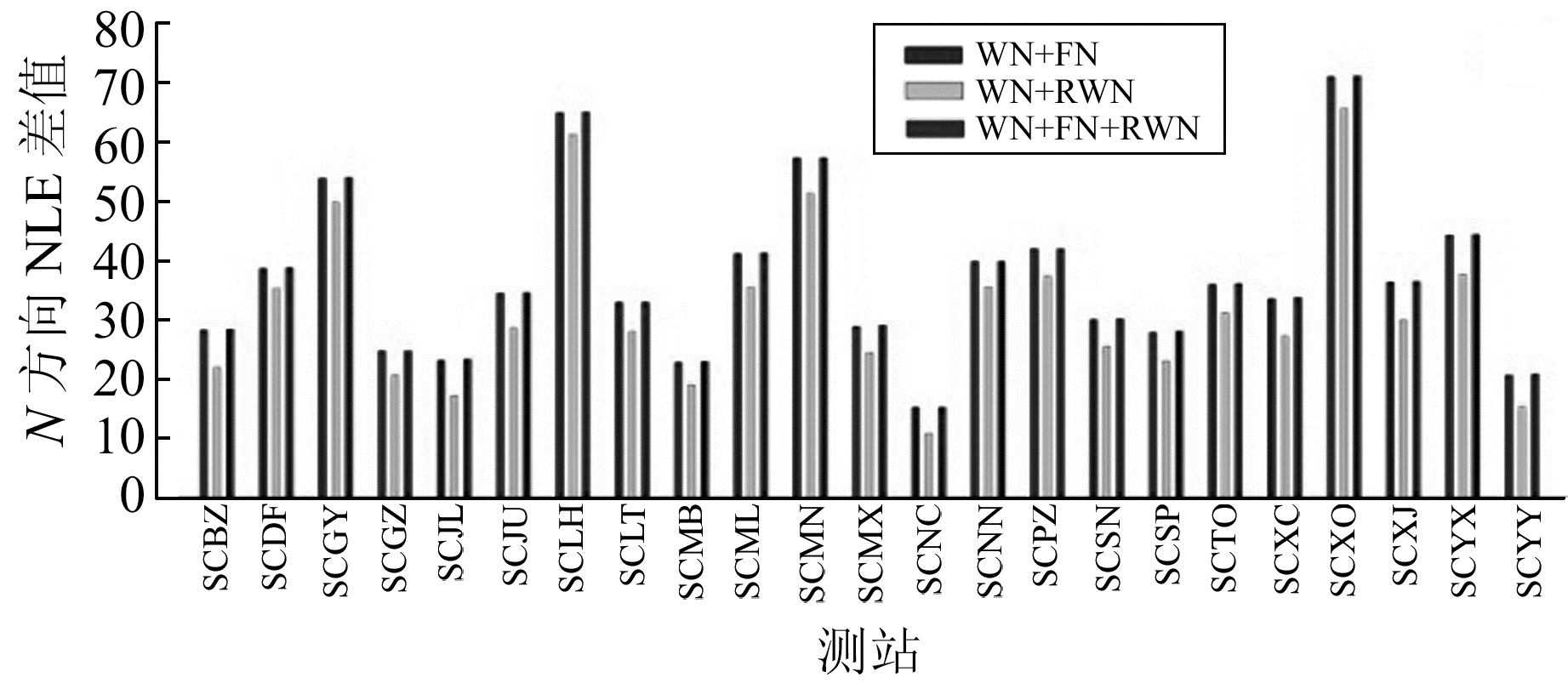
|
图 4 测站E方向最大似然差值 Fig. 4 Maximum likelihood difference of E direction |
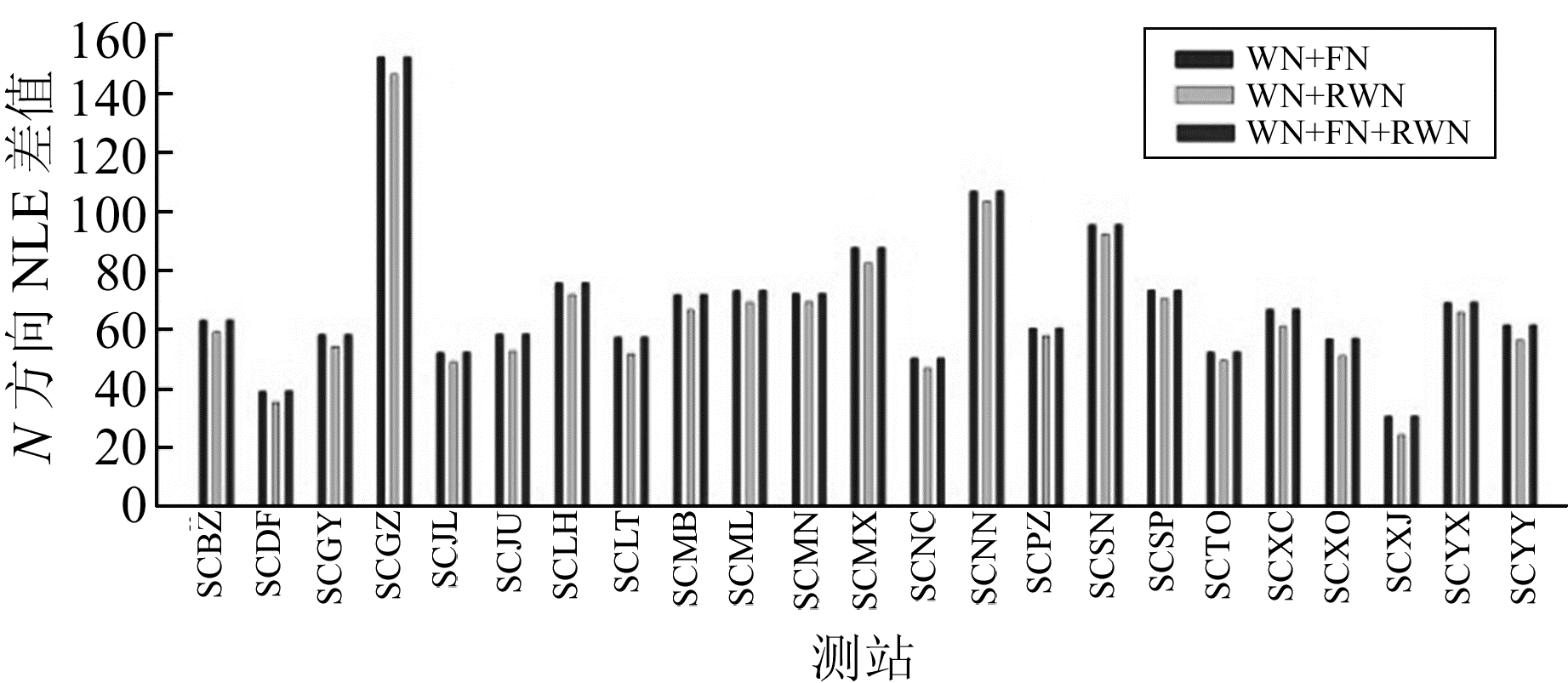
|
图 5 测站U方向最大似然差值 Fig. 5 Maximum likelihood difference of U direction |
由图可见,3种噪声模型组合的最大似然值与WN模型下的最大似然值的差值均大于0,这再次证明四川连续GPS基准站坐标时间序列中既存在白噪声,也包含有色噪声。模型WN+FN和WN+FN+RWN的最大似然值基本相同,均大于WN+RWN噪声模型,这表明在本次实验中测站最佳噪声模型组合为WN+FN或WN+FN+RWN。蒙特卡罗曾通过实验提出,两种模型组合的MLE差值大于2.9作为模型显著区分的阈值[7]。因此,噪声模型组合WN+FN与WN+FN+RWN不具有可分性。为了估计测站各类噪声的大小,假设最佳噪声模型组合为WN+FN+RWN,通过计算该模型下测站的噪声分量,即可判断噪声组合中是否存在RWN。限于篇幅,表 2(单位mm)仅列出其中10个GPS站滤波前后基于噪声组合模型WN+FN+RWN的坐标时间序列在N、E、U 3个方向上的噪声参数估值。
|
|
表 2 基于WN+FN+RWN模型的GPS站坐标时间序列噪声参数估值 Tab. 2 Estimation of noise parameters of GPS station coordinate time series based on WN+FN+RWN model |
由表 2可以看出:
1) 四川连续GPS基准站坐标时间序列的3个坐标分量的噪声特征并不完全相同。表中10个测站滤波后的时间序列在N、U方向上只包括白噪声和闪烁噪声,而在E方向,还有5个测站存在随机游走噪声。因此相对合理的方案是N、U方向采用WN+FN为最佳噪声组合,采用WN+FN+RWN为E方向上的最佳噪声组合。E方向出现随机游走噪声而N、U方向却不存在的原因还有待于进一步研究。
2) 3个坐标分量的噪声性质并不一致,垂直方向上的噪声参数估值明显大于水平方向,这与研究发现的坐标水平分量精度高于垂直方向精度的结论一致。而相比于E方向,N方向上的噪声水平明显要高,尤其是闪烁噪声,这可能与控制点的空间分布有关。
3) 空间滤波可以大幅度降低连续GPS基准站坐标时间序列的白噪声和闪烁噪声的参数估值,同时滤波后测站SCDF、SCXJ、SCYY还出现了随机游走噪声。这表明当闪烁噪声占主导地位时,容易掩盖随机游走噪声,同时也证明了对GPS站坐标时间序列分析时使用滤波除去共模误差的必要性。
4 基于有色噪声的区域速度场分析根据上文对四川连续GPS基准站坐标时间序列噪声分析得到的结论,对其中的10个测站利用最大似然估计法进行速度以及精度估计(见表 3,单位mm/a)。其中北方向、高程方向采用WN+FN模型,东方向采用WN+FN+RWN模型组合。
|
|
表 3 ITRF05框架下部分四川连续GPS基准站点速度 Tab. 3 The speed of the continuous GPS reference station in Sichuan under the framework of ITRF05 |
由表 3可知,在采用最佳模型组合的情况下,各测站N方向上的速度均在6.5~8.5 mm/a,E方向的速度均在31.5~34.5 mm/a,站间差距小于3 mm/a,说明水平总速度在空间分布比较均匀; 而在U方向,测站SCMX相对较大。顾及有色噪声估计的速度中误差明显大于仅考虑白噪声情况下的速度中误差,因此仅考虑白噪声获取的速度精度并不能反映速度场的实际精度。
此外,仅考虑白噪声得到的速度估值与顾及有色噪声获取的速度估值也存在偏差,其中各个测站在两种模型中N、E、U 3个方向速度估值的平均偏差为0.46 mm/a、0.48 mm/a、0.62 mm/a。因此,在根据GPS站坐标时间序列估计基准站速度时,应当顾及有色噪声的影响。
5 结语1) 谱指数计算可以用来分析时间序列中幂指数噪声的大概类型。利用CATS软件获取了滤波后的四川连续GPS基准站时间序列的谱指数,结果表明,四川区域网中23个GPS站各坐标分量的噪声谱指数均介于-1~0,说明这些测站的噪声模型并非单一的噪声模型,而是包括白噪声在内的几种噪声模型的组合。
2) 基于蒙特卡罗准则下的选取标准,通过极大似然估计法估计滤波后GPS站坐标时间序列的最大似然值以及N、E、U方向上噪声参数估值发现,N、U方向上存在白噪声和闪烁噪声,此外E方向还同时存在随机游走噪声。结果表明,对于四川连续GPS基准站坐标时间序列,N、U方向采用WN+FN为最佳噪声组合,使用WN+FN+RWN为E方向上的最佳噪声组合。
3) 空间滤波可以大幅度降低坐标时间序列的白噪声和闪烁噪声的参数估值,同时滤波后一些测站还出现了随机游走噪声,这说明了对GPS站坐标时间序列分析时使用滤波除去共模误差的必要性。
4) 顾及有色噪声时估计的速度中误差明显大于仅考虑白噪声情况下的速度中误差。因此,仅考虑白噪声获取的速度精度并不能反映速度场的实际精度。此外,仅考虑白噪声得到的速度估值与顾及有色噪声获取的速度估值也存在偏差。因此,在根据GPS站坐标时间序列估计基准站速度时,应当顾及有色噪声的影响。
| [1] |
李昭, 姜卫平, 刘鸿飞, 等. 中国区域IGS基准站坐标时间序列噪声模型建立与分析[J]. 测绘学报, 2012, 41(4): 4 96-503 (Li Zhao, Jiang Weiping, Liu Hongfei, et al. Noise Model Establishment and Analysis of IGS Reference Station Coordinate Time Series Inside China[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 4 96-503)
(  0) 0) |
| [2] |
Zhang J, Bock Y, Johnson H, et al. Southern California Permanent GPS Geodetic Array: Error Analysis of Daily Position Estimates and Site Velocities[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B8): 18 035-18 055 DOI:10.1029/97JB01380
(  0) 0) |
| [3] |
Nikolaidis R. Observation of Geodetic and Seismic Deformation with the Global Positioning System[M]. California: Scripps Institution of Oceanography, 2002
(  0) 0) |
| [4] |
姚宜斌, 施闯. IGS测站的非线性变化研究[J]. 武汉大学学报:信息科学版, 2007, 32(5): 423-426 (Yao Yibin, Shi Chuang. On Non-Linear Motion of IGS Station[J]. Geomatocs and Information Science of Wuhan University, 2007, 32(5): 423-426)
(  0) 0) |
| [5] |
蒋志浩, 张鹏, 秘金钟, 等. 顾及有色噪声影响的CGCS2000下我国CORS站速度估计[J]. 测绘学报, 2010, 39(4): 3 55-363 (Jiang Zhihao, Zhang Peng, Bei Jinzhong, et al. Velocity Estimation on the Colored Noise Properties of CORS Network in China Based on the CGCS2000 Frame[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 3 55-363)
(  0) 0) |
| [6] |
Williams S. CATS: GPS Coordinate Time Series Analysis Software[J]. GPS Solutions, 2008(12): 147-153
(  0) 0) |
| [7] |
Mandelbrot B, Ness J. Fractional Brownian Motions, Fractional Noise, and Application[J]. Siam Rev, 1968, 10(4): 422-439 DOI:10.1137/1010093
(  0) 0) |
| [8] |
Langbein J. Noise in GPS Displacement Measurements from Southern California and Southern Nevada[J]. Journal of Geophysical Research:Solid Earth, 2008, 113(B5): 620-628
(  0) 0) |
| [9] |
Williams S D P, Willis P. Error Analysis of Weekly Station Coordinate in the DORIS Network[J]. Journal of Geodesy, 2006, 80(8-11): 525-539 DOI:10.1007/s00190-006-0056-6
(  0) 0) |
| [10] |
苏利娜, 丁晓光, 张彦芬, 等. 陕西连续GPS基准站坐标时间序列分析[J]. 大地测量与地球动力学, 2014, 34(5): 106-109 (Su Lina, Ding Xiaoguang, Zhang Yanfen, et al. Study on Coordinate Time Series of Shanxi Continuous GPS Reference Stations[J]. Journal of Geodesy and Geodynamics, 2014, 34(5): 106-109)
(  0) 0) |
| [11] |
王敏, 沈正康, 董大南. 非构造形变对GPS连续站位置时间序列的影响和修正[J]. 地球物理学报, 2005, 48(5): 1 045-1 052 (Wang M, Shen Z K, Dong D N. Effects of Non-tectonic Crustal Deformation on Continuous GPS Position Time Series and Correction to Them[J]. Chinese J Geophys, 2005, 48(5): 1 045-1 052)
(  0) 0) |
2. College of Geomatics, Shandong University of Science and Technology, 579 Qianwangang Road, Qingdao 266590, China
 2018, Vol. 38
2018, Vol. 38

