对流层延迟泛指电磁波信号在通过高度为50 km以下的未被电离的大气时所产生的延迟误差,是GNSS精密定位的主要误差源之一。一般认为,在GPS短基线解算时,由于测站距离较近,对流层延迟高度相关,采用双差的方法可以基本消除。但当高差较大时,两个测站的大气状态不再相关, 差分后残余的对流层延迟将影响基线解的精度, 甚至影响整周模糊度的固定[1]。近年来,在短基线测量中因竖直方向气象差异引起的残余对流层延迟误差已逐步引起重视。舒海翅等[2]比较了河谷地区有无对流层延迟改正时GPS短基线解算结果, 发现对流层延迟影响的大小与测站两端高差大小以及测站所处环境有关; 安向东等[3]就高差对GPS基线解算结果进行分析,发现高差对基线的U分量具有显著影响,而通过引入一个对流层参数可明显削弱其影响。以上文献主要针对GPS短时段解算结果,而对长时间跨度的解算结果研究较少。为此,本文选取位于不同地区、高差不同的5组GPS短基线作为研究对象,采用GAMIT10.6软件,使用估计与不估计对流层延迟两种方案进行基线解算。对两种方案得到的基线时间序列进行比较,讨论估计对流层与否对长时段基线解算结果的影响。
1 对流层延迟估计方法对流层延迟的90%是由大气中干燥气体引起的, 称为干分量; 其余10%是由水汽引起的, 称为湿分量。由于大气层中的水汽分布在时间和空间上变化很大, 其折射误差很难准确地预测。因此, 湿分量成为制约对流层延迟改正精度的主要因素[4]。天顶方向的对流层延迟用干、湿两分量及其映射函数表示为:
| $ \Delta {{D}_{\text{trop}}}=\Delta {{D}_{\text{z, dry}}}{{M}_{\text{dry}}}\left( E \right)+\Delta {{D}_{\text{z, wet}}}{{M}_{\text{wet}}}\left( E \right) $ | (1) |
式中, ΔDtrop为对流层延迟; ΔDz, dry、ΔDz, wet为天顶方向对流层延迟的干、湿分量; Mdry(E)、Mwet(E)为天顶方向对流层延迟干湿分量相应的映射函数。以上将对流层延迟误差写成天顶延迟改正和映射函数乘积形式的方法称为模型函数法,该方法是基于“任意方向上的路径延迟均与天顶方向路径有关”的假设。目前常用的基于映射函数的对流层延迟模型有ECMWF/VMF1模型、GPT/GPM模型、GPT2模型等。本文采用Saastamoinen模型估计干湿分量初值,选用GPT/GPM模型计算对应的映射函数。
由于映射函数通常都是基于大气球对称假设而建立的,而这与实际大气状况存在一定的差距,为此GAMIT引入了大气梯度的概念,以进一步减弱由此造成的影响。在其solve模块中采用的梯度模型表达式为[5]:
| $ \Delta L\left( \text{ }\!\!\varepsilon\!\!\text{ }, \varphi \right)=\frac{{{G}_{\text{NS}}}\cos \left( \varphi \right)+{{G}_{\text{EW}}}\sin \left( \varphi \right)}{\left( \sin \left( \varepsilon \right)\tan \left( \varepsilon \right)+0.003 \right)} $ | (2) |
式中,ε为高度角,φ为方位角,GNS和GEW分别为南北、东西方向的梯度。
GAMIT估计对流层延迟的方法主要是分段常数法和分段线性函数法。分段常数法的思路是将整个观测时段分为N个子时段, 每个子时段内有n个观测历元,对每个子时段引入一个附加的对流层参数,并认为对流层延迟在该子时段内是一个常数[3]。由于该方法引入的未知参数较少,适用于观测时段较短、气候稳定的情况[4]。分段线性函数法的思路是假定在两个节点之间的时段上,测站天顶方向的对流层延迟随时间线性变化,从而估计节点处对流层延迟参数[6],适用于GPS观测时段较长、气候变化较规则的场合[4]。
2 实验数据及处理策略数据来源于SOPAC(http://sopac-ftp.ucsd.edu/pub/)提供的部分IGS站在ITRF2008框架下的2005~2007年观测数据。为研究对流层延迟对短基线时间序列的影响,选取的IGS站有:位于美国的测站CIT1、JPLM、WLSN,位于俄罗斯的测站PETP、PETS,位于日本的测站KGNI、MTKA。这些测站都靠近北太平洋,且位于同一区域的测站距离较近。为比较高差不同的短基线受对流层延迟改正影响的大小,选取的测站间高差存在差异,具体情况见表 1。
|
|
表 1 有无对流层延迟改正的U方向解算结果比较 Tab. 1 Comparison of U component with or without tropospheric delay correction |
利用GAMIT10.6对上述IGS站组成的短基线进行基线解算,对作为起算点的IGS站采用强约束,N、E、U方向的约束量均为0.05 m。卫星轨道为固定轨道,观测值类型选取LC_AUTCLN, 数据采样间隔为30s。对同一条基线,分别采用两种方案进行解算:方案1,同时估计对流层延迟和梯度,估计对流层参数时采用分段线性函数法,在sestbl.文件中设置zenith delay estimation=Y和atmospheric gradients=Y,每隔2 h估计一个对流层参数; 方案2,估计梯度、不估计对流层延迟,此时设置zenith delay estimation=N和atmospheric gradients=Y。采用上述策略,分别使用两种方案对IGS站2005~2007年共1 095 d的观测数据进行基线解算,得到强约束下的单天解(保存在GAMIT的Q文件和O文件中),从而得到时间跨度为3 a的基线时间序列。对得到的时间序列进行处理时,首先要剔除误差较大的点,同时要对缺失的数据进行插值补齐。通过对比发现,三次多项式插值方法能使数据基本保持原有的趋势,故本文采用这种方法。
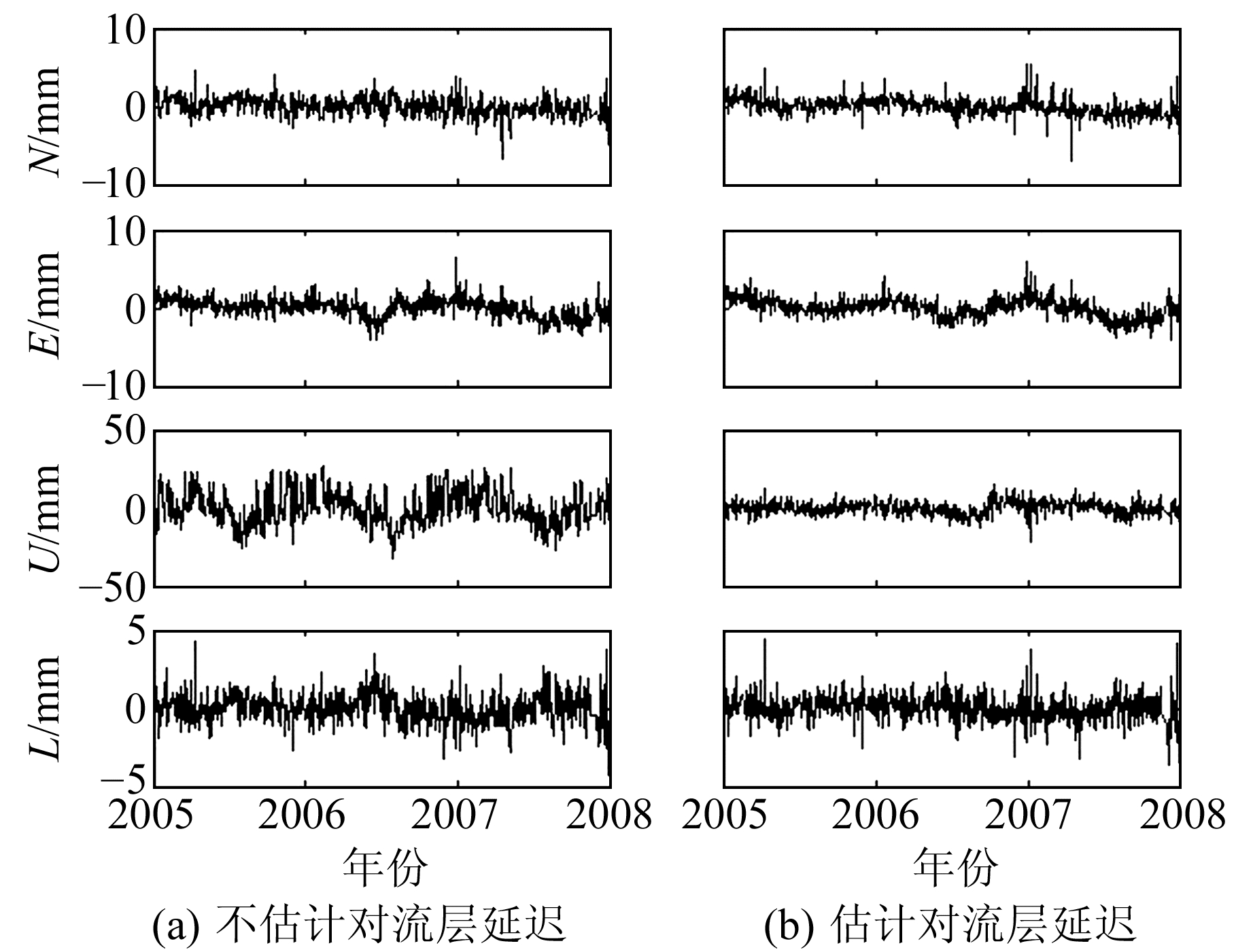
3 结果分析 3.1 估计与不估计对流层参数时间序列比较经过上述处理后,对同一条基线,分别得到两种方案解算得到的时间序列,然后去除阶跃项、趋势项等构造信号引起的位移。以基线CIT1-JPLM为例(图 1),采用两种方案得到的时间序列中,U方向3 a内的变化量级均比N、E方向以及基线长度L的变化量级大。对比两种方案下各分量的时间序列发现,对流层估计与否对N、E方向和基线长度L的影响较小,而对U方向的影响较大,这与相应理论一致。由于高程方向最易受环境影响,本文着重研究对流层延迟改正对基线高程方向的影响。
|
图 1 基线CIT1-JPLM的时间序列 Fig. 1 Time series of CIT1-JPLM baseline |
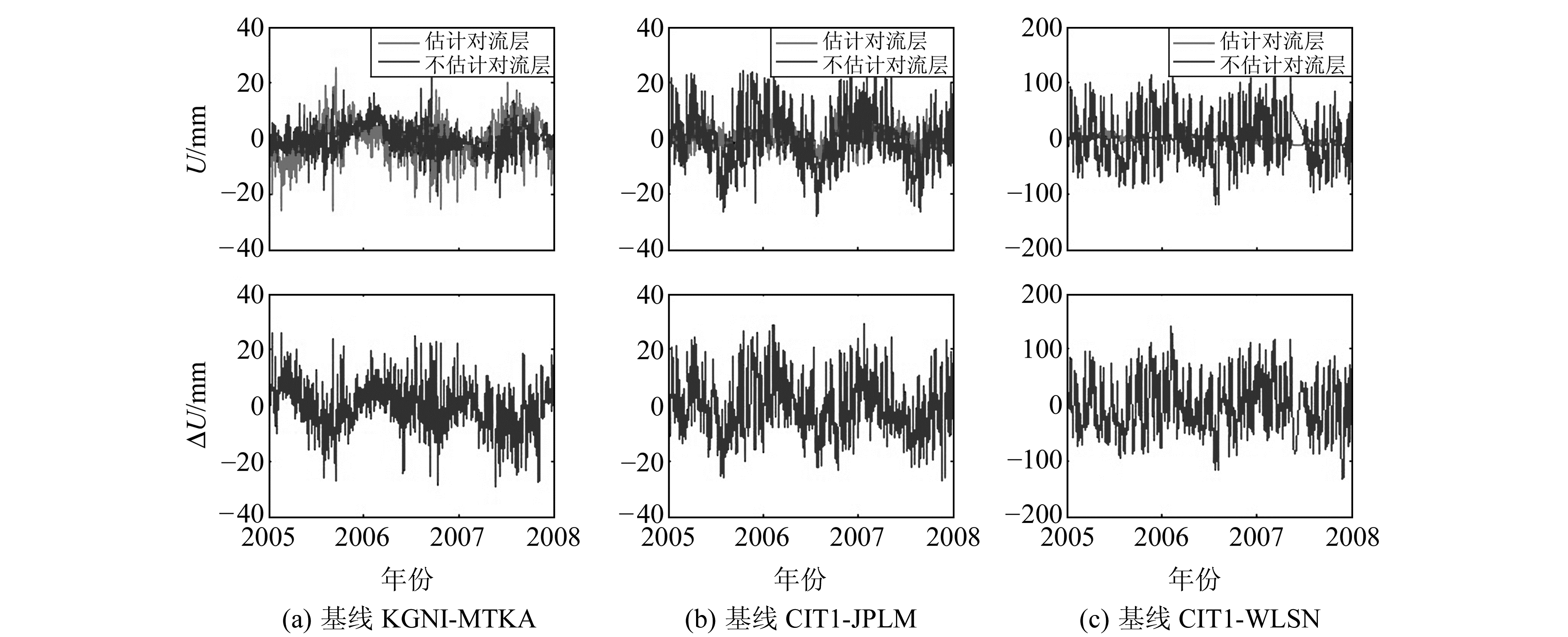
将各基线高程方向估计与不估计对流层参数得到的时间序列进行比较,然后将两者相减得到两种解算模式下的高程分量偏差ΔU的时间序列,部分基线结果如图 2所示。由图 2可知,对测站间高差较小(14.5 m)的基线KGNI-MTKA, 相对于高差较大的基线,估计与不估计对流层延迟对解算结果的影响较小; 基线CIT1-JPLM测站间高差达到了208.6 m,影响量级为cm级,与基线KGNI-MTKA相当; 而对于高差达到1 km以上的基线CIT1-WLSN,估计与不估计对流层延迟对解算结果的影响相对前两条基线明显较大。所有基线的基本信息以及两种解算方案的比较如表 1所示。
|
图 2 基线U方向分量及其较差 Fig. 2 U component of some baselines and its offset |
由表 1可以发现,随着基线长度和高差的增大,U方向较差一般也随之增大。基线KGNI-MTKA高差仅为14.5 m,较差最大值却接近3 cm。这说明,当基线两端的高差不是很大时,测站间水平距离以及所处的复杂环境也会使得基线两端的气象差异较大。对于高差达到1 km以上的基线JPLM-WLSN和CIT1-WLSN,估计对流层延迟与否对高程方向影响最大可达到dm级,平均较差为cm级,此时U方向较差偏大主要是由站间高差较大所引起的。由于沿海地区大气水汽随时间变化复杂,天顶延迟变化剧烈,对流层延迟改正与否对基线解算结果影响一般较大。
3.2 高程方向周期性分析由于GPS基线时间序列能在一定程度上削弱系统误差和共模噪声影响,因此比单个测站坐标时间序列更能反映周围构造环境的变化[7]。GPS坐标时间序列呈现显著的非线性变化(尤其是垂直方向的季节性变化),通常认为地球物理效应及与GPS技术相关的系统误差是造成测站非线性变化的主要因素[8]。由图 2看出,方案2(不估计对流层延迟)得到的高程方向时间序列周年振幅明显大于方案1(估计对流层延迟)。
小波变换利用多尺度分析的原理,可以将时间序列几乎无损地分解成低频部分和高频部分,再将分解后的信号投射到不同的尺度上进行研究,尤其适合处理非平稳时间序列。为分析高程方向时间序列中存在的季节信号,有必要利用小波变换在时域内进行分析[9-10]。在进行小波变换时,需要选定合适的小波基函数与分解层次,本文采取coif小波作为基函数,分解层次为8层。
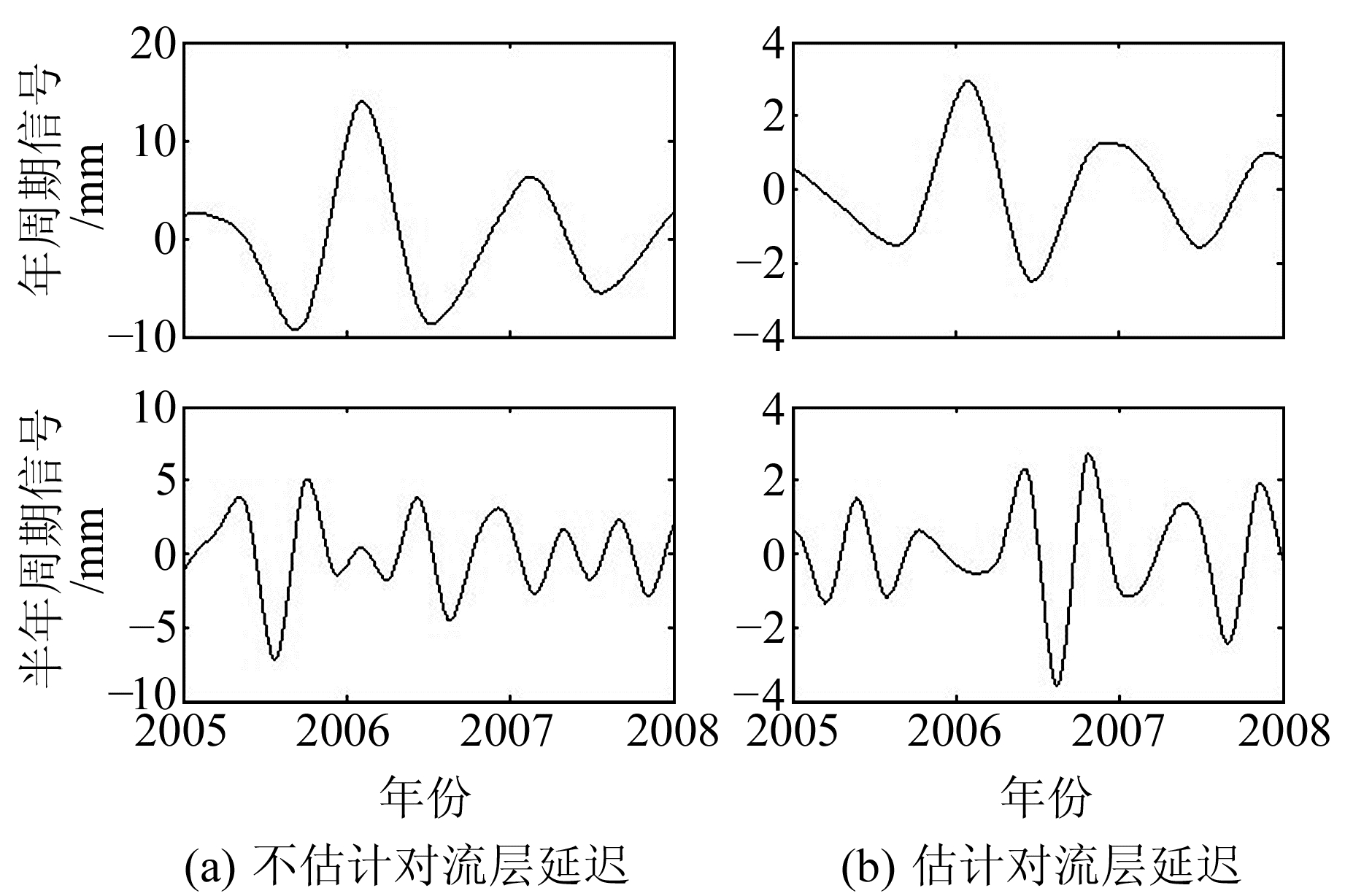
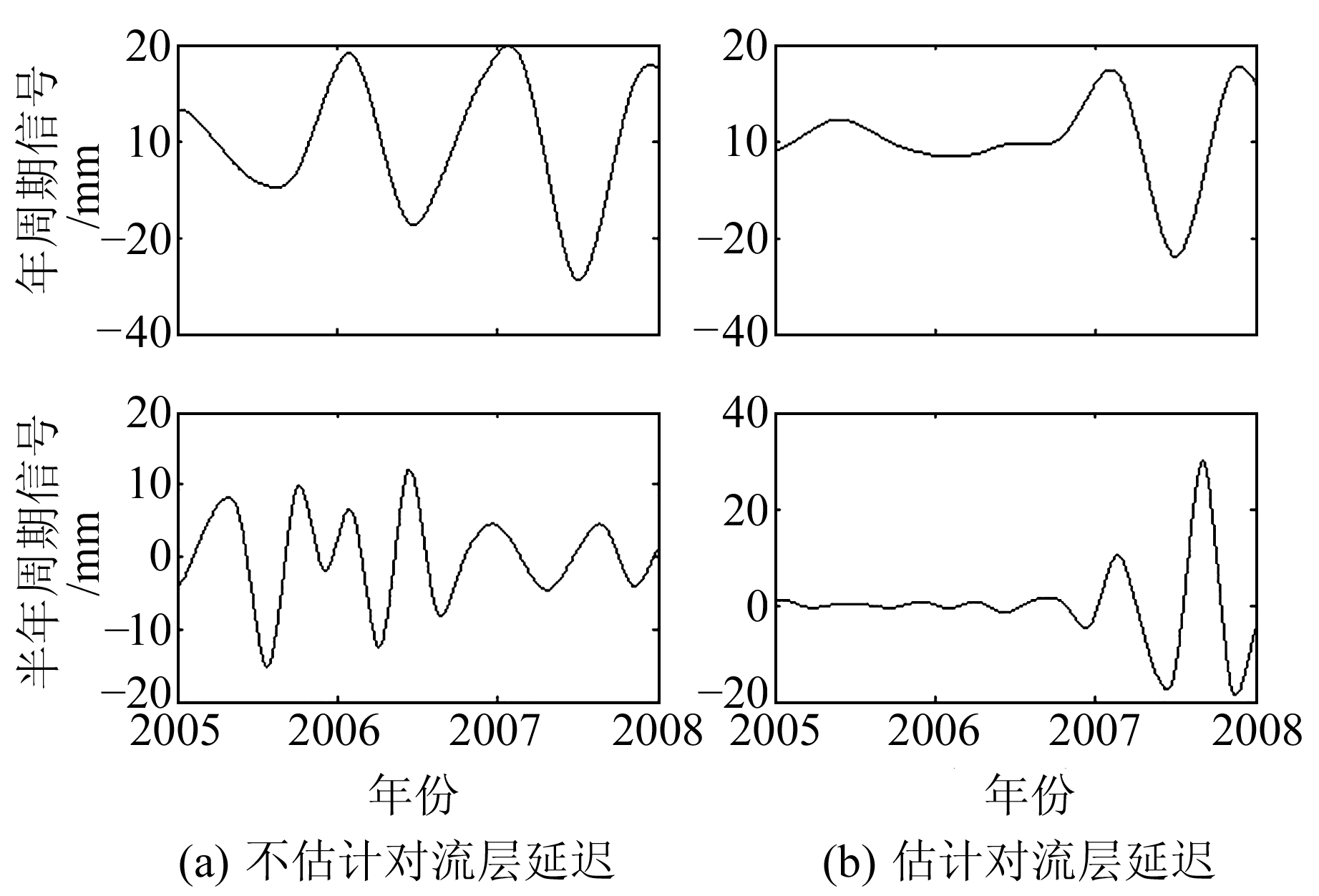
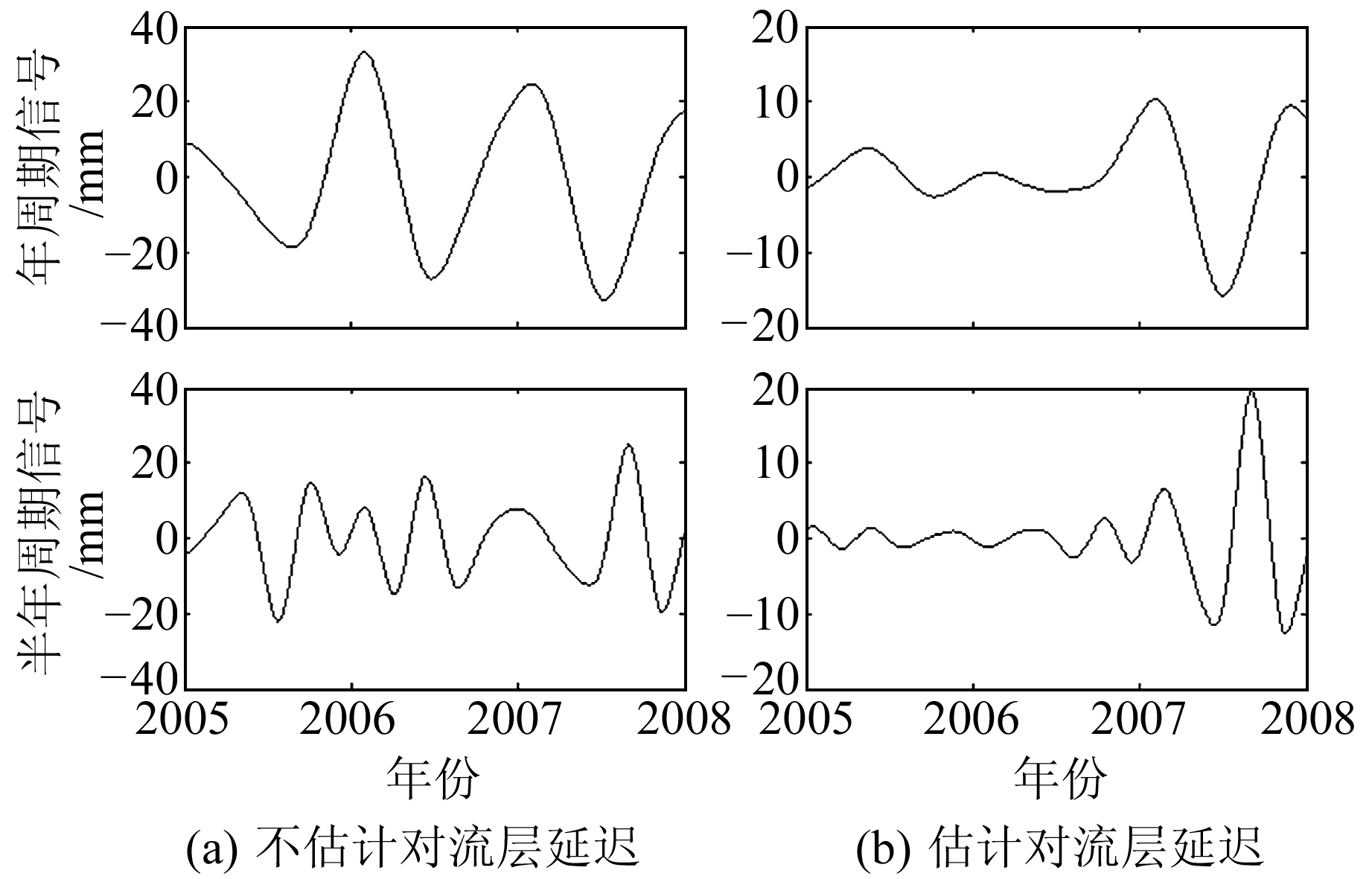
图 3~5分别表示基线CIT1-JPLM、JPLM-WLSN、CIT1-WLSN进行小波变化的结果,各基线的高程方向时间序列一般存在周年、半周年的周期特性,且其振幅随时间变化。对同一条基线,对比两种方案解算结果可以发现,不估计对流层延迟时,基线高程方向时间序列存在振幅较大的周年信号,而估计对流层延迟后该周年信号明显减小。为了更加直观地分析对流层延迟对高程方向时间序列中季节信号幅值的影响,分别估计两种方案周年、半周年振幅,如表 2所示。
|
图 3 基线CIT1-JPLM小波变换结果 Fig. 3 Wavelet analysis of CIT1-JPLM baseline |
|
图 4 基线JPLM-WLSN小波变换结果 Fig. 4 Wavelet analysis of JPLM-WLSN baseline |
|
图 5 基线CIT1-WLSN小波变换结果 Fig. 5 Wavelet analysis of CIT1-WLSN baseline |
|
|
表 2 基线周年、半周年振幅 Tab. 2 Annual and semi annual amplitude of the baseline |
由表 2可知,对于高差较小的基线KGNI-MTKA,高程方向时间序列季节变化的振幅在对流层延迟改正前后变化不大。而对于其他高差较大(大于100 m)的基线,方案2解算后的周年振幅明显大于方案1,且随着高差的增大,振幅的差值也随之增大。高差在100~200 m左右的两条基线PETS-PETP、CIT1-JPLM,不估计对流层延迟时出现了平均振幅接近8 mm的周年信号,而估计对流层时平均周年振幅减小到4 mm以内。高差1 km以上的基线JPLM-WLSN和CIT1-WLSN,不估计对流层延迟使高程方向时间序列分别产生了平均周年振幅16.8 mm和24.1 mm的季节信号; 而估计对流层后,季节信号的平均周年振幅仅为8.9 mm和6.4 mm,基线CIT1-WLSN的周年振幅差值达到了17.7 mm。相比周年信号,半周年信号的振幅在改正前后变化不大,一般在2 mm左右,仅有基线CIT1-WLSN的半周年振幅差值达到9.4 mm。因此可以认为,在对高差大于100 m的基线进行基线解算时,不估计对流层延迟会使高程方向时间序列出现周年振幅较大的虚假季节变化。不估计对流层延迟时,时间序列中季节变化包含有来自基线两端天顶对流层延迟差异带来的影响,测站之间这段大气的周期性变化是造成方案2高程时间序列出现虚假季节变化的原因。当然,一些未模型化或模型化不准的半周日和周日信号也可能会形成假频长周期信号传播到长周期项中。
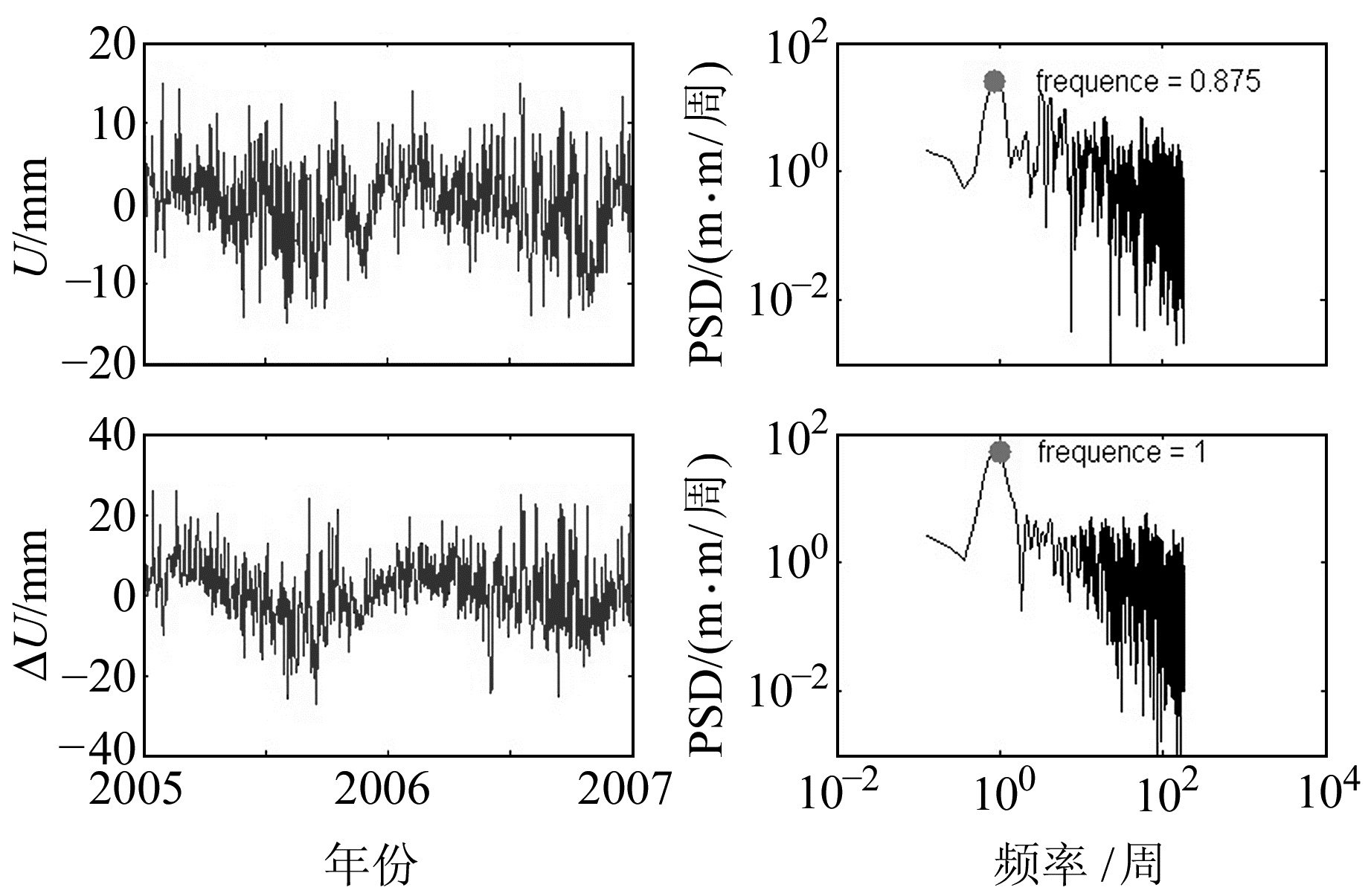
基线两端天顶对流层总延迟求差,可以得到测站之间相对天顶对流层延迟(RZTD)。当不估计对流层延迟时,默认测站间对流层延迟相同; 而估计对流层延迟时,RZTD表现出随时间变化。将两种方案的RZTD作差得到ΔRZTD。章迪等[11]采用只估计对流层延迟、不估计梯度和对流层延迟及梯度均不估计两种方案对基线进行解算,发现ΔRZTD与基线高程方向较差ΔU存在相关性,ΔRZTD所造成的高程方向偏差大致为自身的3倍。本文采用的两种方案均估计梯度,通过比较几组基线的ΔRZTD和ΔU的均值发现,ΔU大致为ΔRZTD的2倍。由此说明,GAMIT解算时,估计梯度对结果有一定的改善作用。以基线KGNI-MTKA为例,比较其ΔRZTD和ΔU的时间序列,并得到两者的功率谱周期图,如图 6所示。
|
图 6 基线KGNI-MTKA的ΔRZTD和ΔU及功率谱周期图 Fig. 6 ΔRZTD and ΔU of KGNI-MTKA baseline and their power spectrum periodogram |
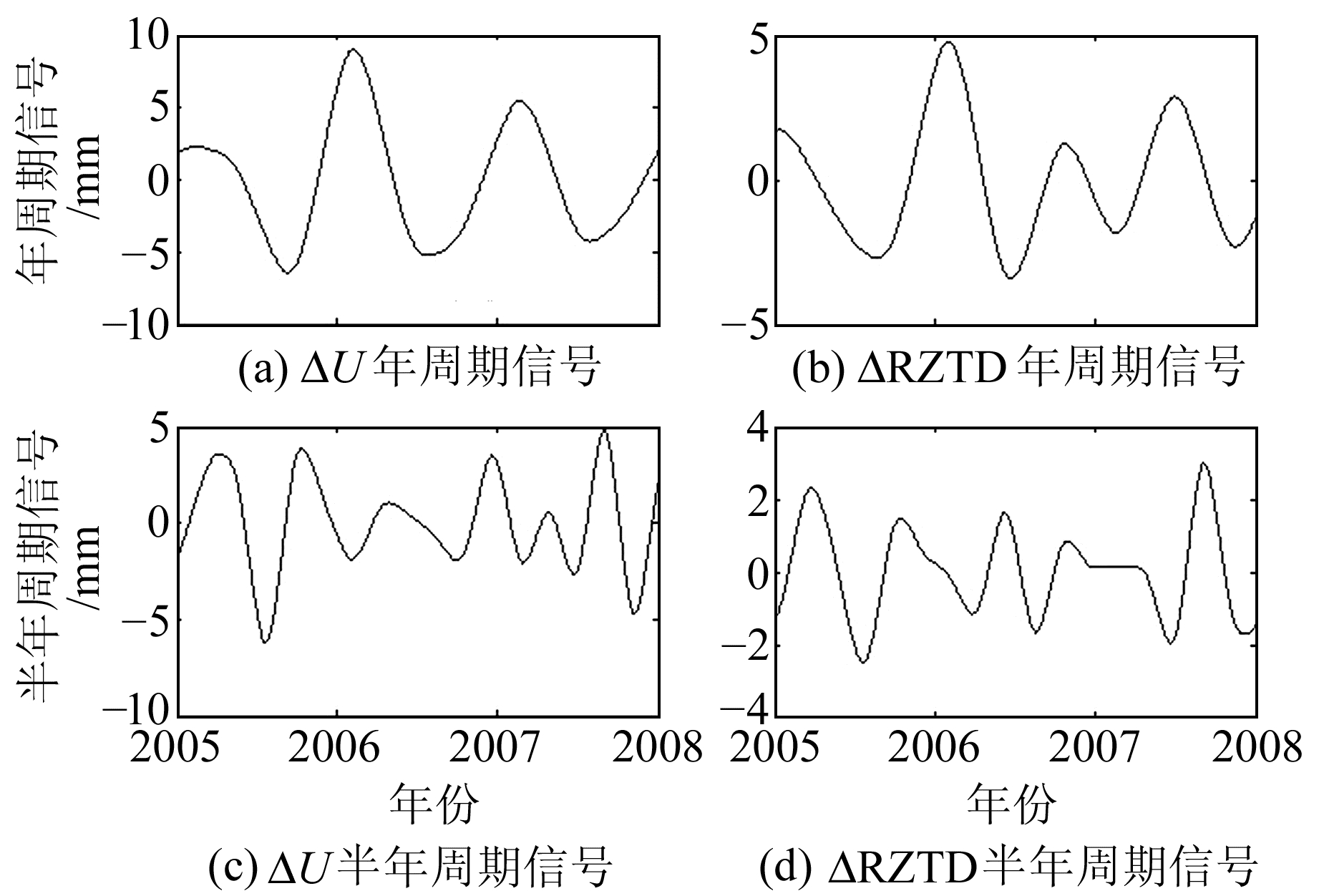
由图 6可知,基线KGNI-MTKA的ΔU和ΔRZTD变化趋势有一定的相关性,并可以明显看出两者均有强而平稳的周年性波动趋势。由功率谱周期图可知,两者的时间序列都存在与时间相关的噪声,在低频处能量较大,呈现出明显的峰值。其中ΔU和ΔRZTD的时间序列第一个峰值对应的倍率约为1周,与周年项大体对应,这说明序列存在周年信号,而半周年信号不明显。对基线KGNI-MTKA的ΔU和ΔRZTD进行小波变换,如图 7所示。
|
图 7 基线KGNI-MTKA的ΔRZTD和ΔU小波变换结果 Fig. 7 Wavelet analysis of ΔRZTD and ΔU of KGNI-MTKA baseline |
通过各基线ΔU和ΔRZTD的小波变换结果可以发现,它们的周期信号存在一定的相关性。通过计算得到各基线ΔU和ΔRZTD周年项以及半周年项的相关系数,如表 3所示。可以发现,随着测站高差的增大,相关系数有递减的趋势,这可能与高差越大、大气天顶延迟变化越不规则有关,其中深层次的关联还有待进一步研究。
|
|
表 3 ΔU和ΔRZTD周期项的相关系数 Tab. 3 The correlation coefficient of periodic term of ΔU and ΔRZTD |
1) 对流层延迟与测站实际气象条件密切相关,简单地通过基线长度以及测站高差来判断是否进行对流层延迟估计是不够严密的。计算结果表明,高差在1 km之内的几条短基线,不估计对流层延迟会带来cm级的偏差; 而高差在1 km以上的短基线,偏差最大能达到dm级。因此,对一些基线虽短但高差较大的基线,在用GAMIT进行解算时仍需设置对流层估计。
2) 在对高差大于100 m的短基线进行基线解算时,不估计对流层延迟会使高程方向时间序列出现周年振幅较大的虚假季节变化。该虚假季节信号与测站间天顶对流层延迟差异ΔRZTD有关,其周年振幅最大可达17.7 mm; 而估计对流层延迟后,季节信号明显减弱。因此,估计对流层延迟有利于分离构造运动与其他信号,获取可靠的长期运动趋势。
| [1] |
丁晓光. 对流层延迟改正在GPS数据处理中的应用与研究[D]. 西安: 长安大学, 2009 (Ding Xiaoguang. Research of Tropospheric Delay Model and Applications Based on the GPS Data Processing[D]. Xi'an: Chang'an University, 2009)
(  0) 0) |
| [2] |
舒海翅, 郑敏. 河谷区对流层延迟对GPS短基线解算的影响分析[J]. 人民长江, 2010, 41(20): 60-62 (Shu Haichi, Zheng Min. Analysis on Influence of Tropospheric Delay in Rivervalley Area on GPS Short Baseline Resolution[J]. Yangtze River, 2010, 41(20): 60-62 DOI:10.3969/j.issn.1001-4179.2010.20.018)
(  0) 0) |
| [3] |
安向东, 杨登科. 测站间高差对短时段GPS基线解算的影响[J]. 大地测量与地球动力学, 2016, 36(6): 534-538 (An Xiangdong, Yang Dengke. The Impact of the Height Difference between Stations on Baselines Solution of Short Period GPS Observations[J]. Journal of Geodesy and Geodynamic, 2016, 36(6): 534-538)
(  0) 0) |
| [4] |
魏子卿, 葛茂荣. GPS相对定位的数学模型[M]. 北京: 测绘出版社, 1998 (Wei Ziqing, Ge Maorong. The Mathematical Model of GPS Relative Positioning[M]. Beijing: Surveying and Mapping Press, 1998)
(  0) 0) |
| [5] |
Chen G, Herring T A. Effects of Atmospheric Azimuthal Asymmetryon the Analysis of Space Geodetic Data[J]. Journal of Geophysical Research:Solid Earth, 1997, 102(B9): 20 489-20 502 DOI:10.1029/97JB01739
(  0) 0) |
| [6] |
许华冠, 程宗颐. GPS精密定位中对流层折射参数估计方法的比较分析[J]. 中国科学院上海天文台年刊, 1997, 18: 95-102 (Xu Huaguan, Cheng Zongyi. The Comparison and Analysis of the Parameter Estimation Methods of Tropospheric Refraction on GPS Precise Position[J]. Annals of Shanghai Observatory Academia Sinica, 1997, 18: 95-102)
(  0) 0) |
| [7] |
张风霜, 武艳强, 孙东颖. 中国大陆GPS连续观测站基线时间序列分析[J]. 地震, 2011, 31(4): 87-95 (Zhang Fengshuang, Wu Yanqiang, Sun Dongying. Analysis of the Baseline Time Series from Continuous GPS Stations in the Mainland of China[J]. Earthquake, 2011, 31(4): 87-95)
(  0) 0) |
| [8] |
姜卫平, 李昭, 刘鸿飞, 等. 中国区域IGS基准站坐标时间序列非线性变化的成因分析[J]. 地球物理学报, 2013, 56(7): 2 228-2 237 (Jiang Weiping, Li Zhao, Liu Hongfei, et al. Cause Analysis of the Non-Linear Variation of the IGS Reference Station of the IGS Reference Station Coordinate Time Series indide China[J]. Chinese Journal of Geophysics, 2013, 56(7): 2 228-2 237)
(  0) 0) |
| [9] |
黄声享, 刘经南, 柳响林. 小波分析在高层建筑动态监测中的应用[J]. 测绘学报, 2003, 32(2): 153-157 (Huang Shengxiang, Liu Jingnan, Liu Xianglin. Deformation Analysis Based on Wavelet and Its Applicationin Dynamic Monitoring for High-Rise Buildings[J]. Aata Geodaetica et Cartographica Sinica, 2003, 32(2): 153-157)
(  0) 0) |
| [10] |
郭英起, 史大起, 黄声享, 等. 高精度GPS测量中小波分析的应用[J]. 测绘工程, 2009, 18(3): 58-64 (Guo Yingqi, Shi Daqi, Huang Shengxiang, et al. Application Summary of Wavelet Analysis in High-Precision GPS Surveying[J]. Engineering of Surveying and Mapping, 2009, 18(3): 58-64)
(  0) 0) |
| [11] |
章迪, 郭际明, 陈雪丰, 等. 对流层延迟估计对高差较大短基线解算的影响[J]. 大地测量与地球动力学, 2014, 34(2): 147-149 (Zhang Di, Guo Jiming, Chen Xuefeng, et al. Influence of Estimation of Tropospheric Delay on Short Baseline with Big Height Difference[J]. Journal of Geodesy and Geodynamic, 2014, 34(2): 147-149)
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38

