GPS实时动态定位中,卫星数过多并不能使精度显著提升[1],在保证一定精度条件下,顾及实时性的最佳卫星数为6颗[2]。胡耀坤等[3]分析了不同截止高度角对BDS/GPS组合伪距差分定位精度的影响; 张超等[4]提出通过构造与仰角及方位角有关的两个模糊向量作为判据的模糊选星法,但计算量较大; 吴瑞祥等[5]提出选取高度角最大的两颗星为顶座星、高度角小且彼此方位角差分布均匀的4颗星为底座星的六星组合选星法,运算时间较少,但定位精度较差。现有选星方法普遍选择几何精度因子(GDOP)最小的星座组合。为此,通常会选择较低高度角卫星,受大气和多路径效应等影响严重,不利于模糊度快速准确固定,从而使精度较差。本文针对低高度角卫星观测值误差残留问题,提出一种设置高度角阈值的改进六星选星法,探讨其最佳高度角阈值确定策略,并通过BDS/GPS组合定位实例论证所提算法的定位精度及运算效率。
1 改进的六星选星法BDS/GPS相对定位数学模型见文献[6],采用Tuenissen[7]提出的LAMBDA方法进行整周模糊度固定,最终得到高精度坐标固定解。
常规的六星选星法[5]解算效率优势明显,但为了获取较小GDOP需选择高度角较小的卫星,受大气误差和多路径效应等影响严重,定位精度较差。本文提出一种改进的六星选星法:首先根据观测条件设置合理的高度角阈值,把低于阈值的卫星删除; 在剩余卫星中分别选出高度角最高、次高和最低的卫星作为前3颗卫星; 在高度角最低的卫星方位角基础上分别加上(或减去)90°、180°和270°作为判据,在这3个方位角轴线附近选择与其方位角接近、高度角尽可能小的卫星作为其余3颗卫星。评判指标Bj表示为[8]:
| $ {{B}_{j}}={{\tan }^{-1}}\frac{\sqrt{3{{\sin }^{2}}{{E}_{j}}+{{\cos }^{2}}{{E}_{j}}{{\sin }^{2}}{{\beta }_{j}}}}{\cos {{E}_{j}}\sin {{\beta }_{j}}+1} $ | (1) |
式中,Ej为第j颗卫星的高度角; βj为第j颗卫星方位角与设定轴线之间的角度差,βj∈[0°, 180°],如果βj超过180°,则βj=|360°-βj|。
需要说明的是,本文中BDS/GPS组合定位采用的是标准差分技术,即首先在同一系统观测值之间组成站星间双差观测方程,进而进行双系统组合定位,所以选星是在各单系统内进行。如果某一系统卫星数不足6颗,则该系统不执行选星操作,直接利用全部观测值进行组合定位。
2 实验分析 2.1 确定高度角阈值本文通过数值算例确定相对较优的高度角阈值。在不同长度基线下,分别选取7°、10°、15°、20°、25°和30°作为高度角阈值,并将流动站定位结果的均方根误差(RMS)作为精度指标,以处理相同数据所用的平均单历元解算时间作为效率指标,寻找最合适的高度角阈值。
选取香港连续运行参考站网(CORS)中的HKKS、HKWS、HKOH、HKKT、HKSC、HKQT、HKLT、HKSL等8个测站组成5 km、9 km、22 km、27 km基线观测数据,分别设置不同高度角阈值进行处理。观测时间为2016-08-28 00:04~00:05,采样率为1 s。不同高度角下可见卫星数量如表 1所示,不同基线不同高度角阈值下N、E、U定位精度如图 1~4所示。
|
|
表 1 不同高度角下可见卫星数量变化 Tab. 1 The number of satellites changes at different elevation angles |
|
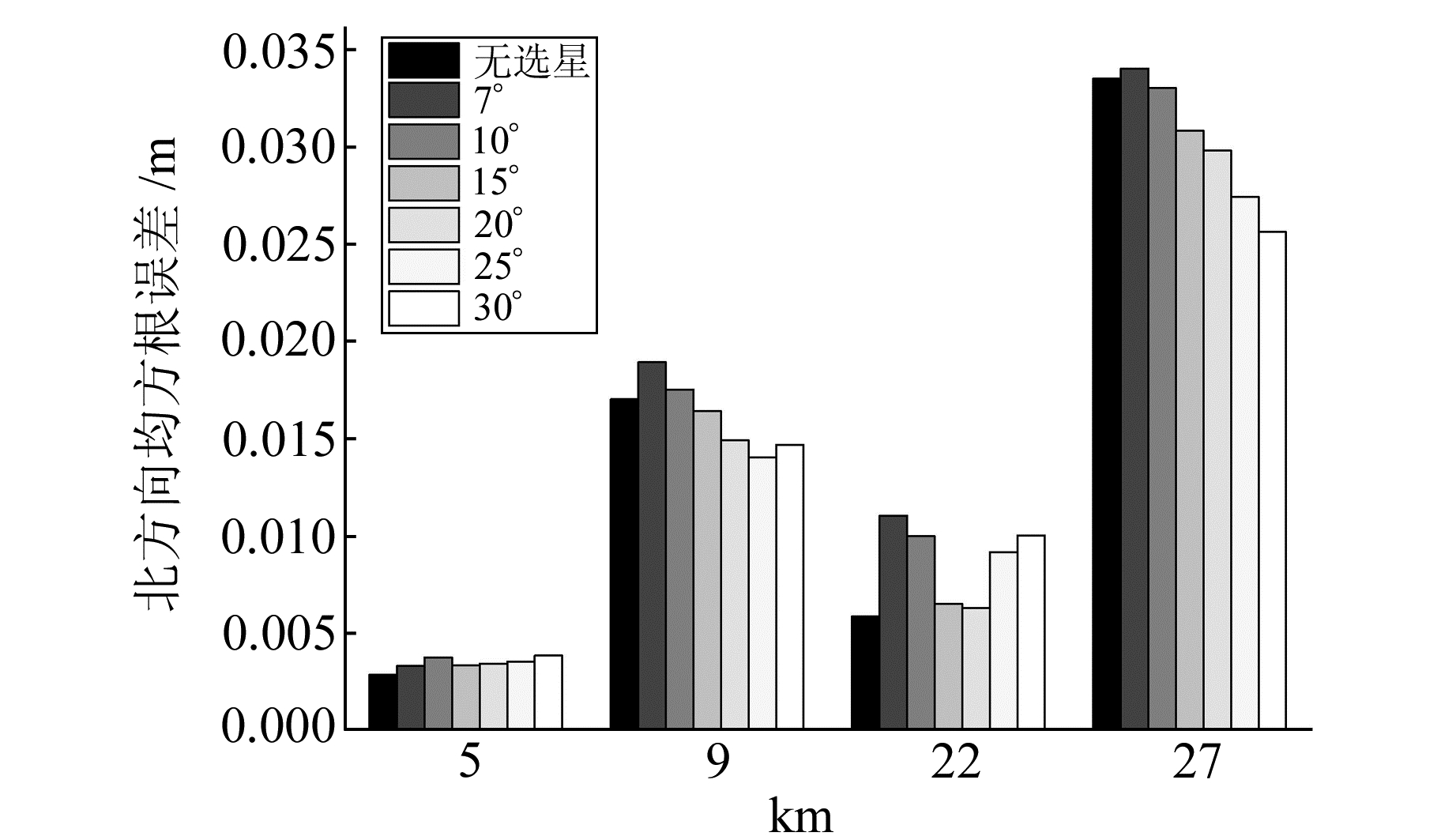
图 1 不同基线不同高度角阈值下北方向定位精度 Fig. 1 The accuracy of N-direction positioning at different elevation angles of different baselines |
|
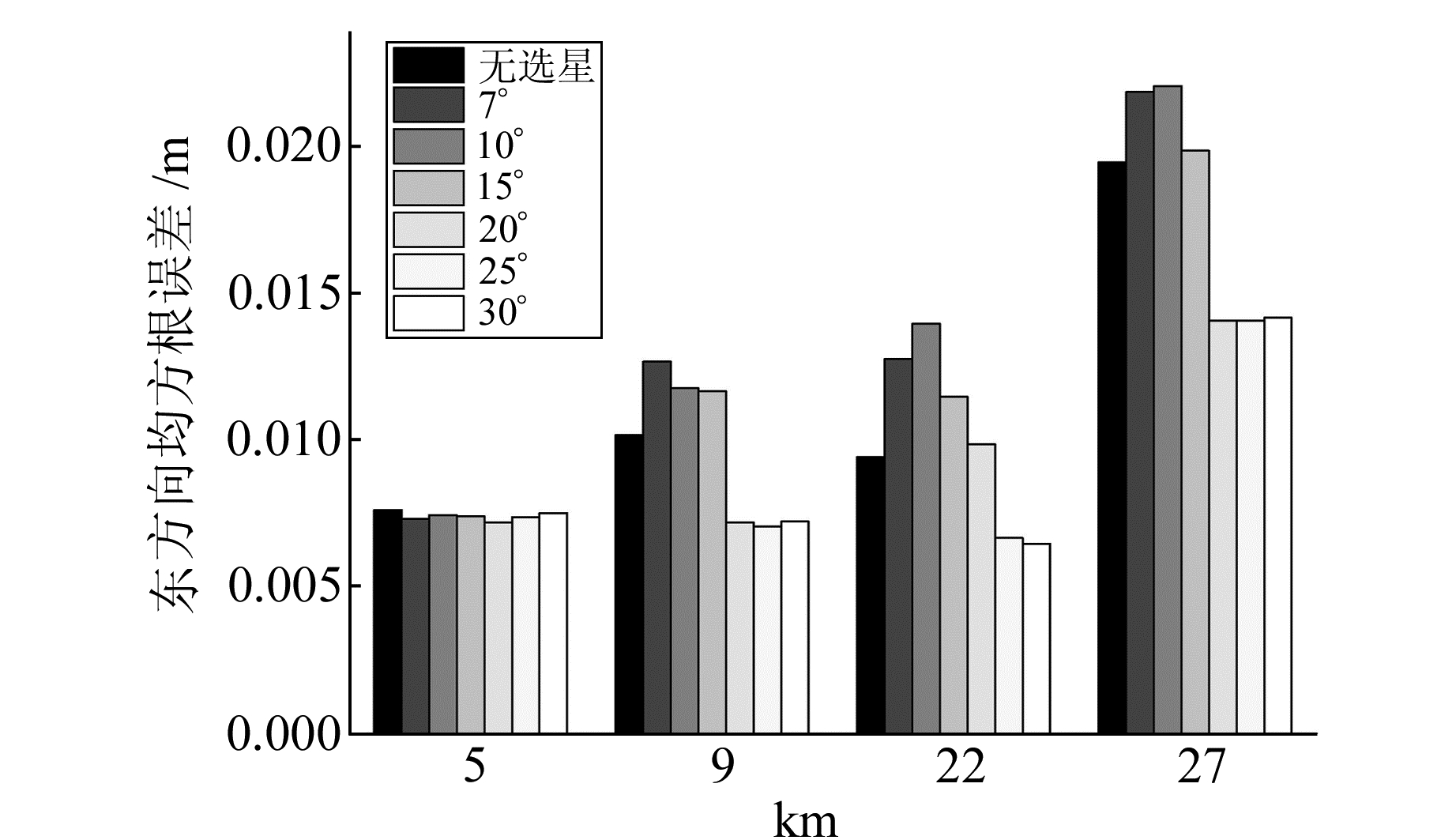
图 2 不同基线不同高度角阈值下东方向定位精度 Fig. 2 The accuracy of E-direction positioning at different elevation angles of different baselines |
|
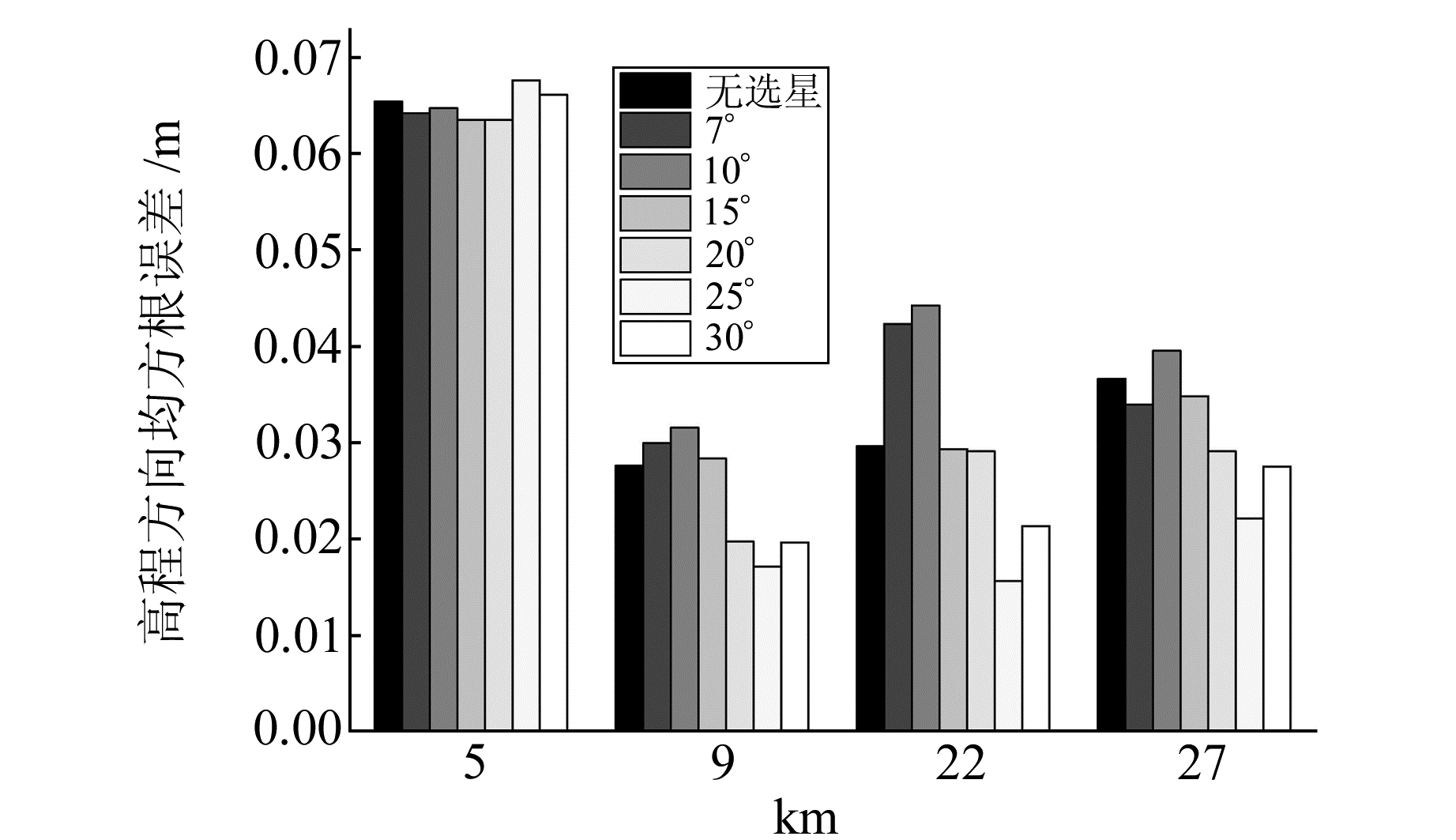
图 3 不同基线不同高度角阈值下高程方向定位精度 Fig. 3 The accuracy of U-direction positioning at different elevation angles of different baselines |
|
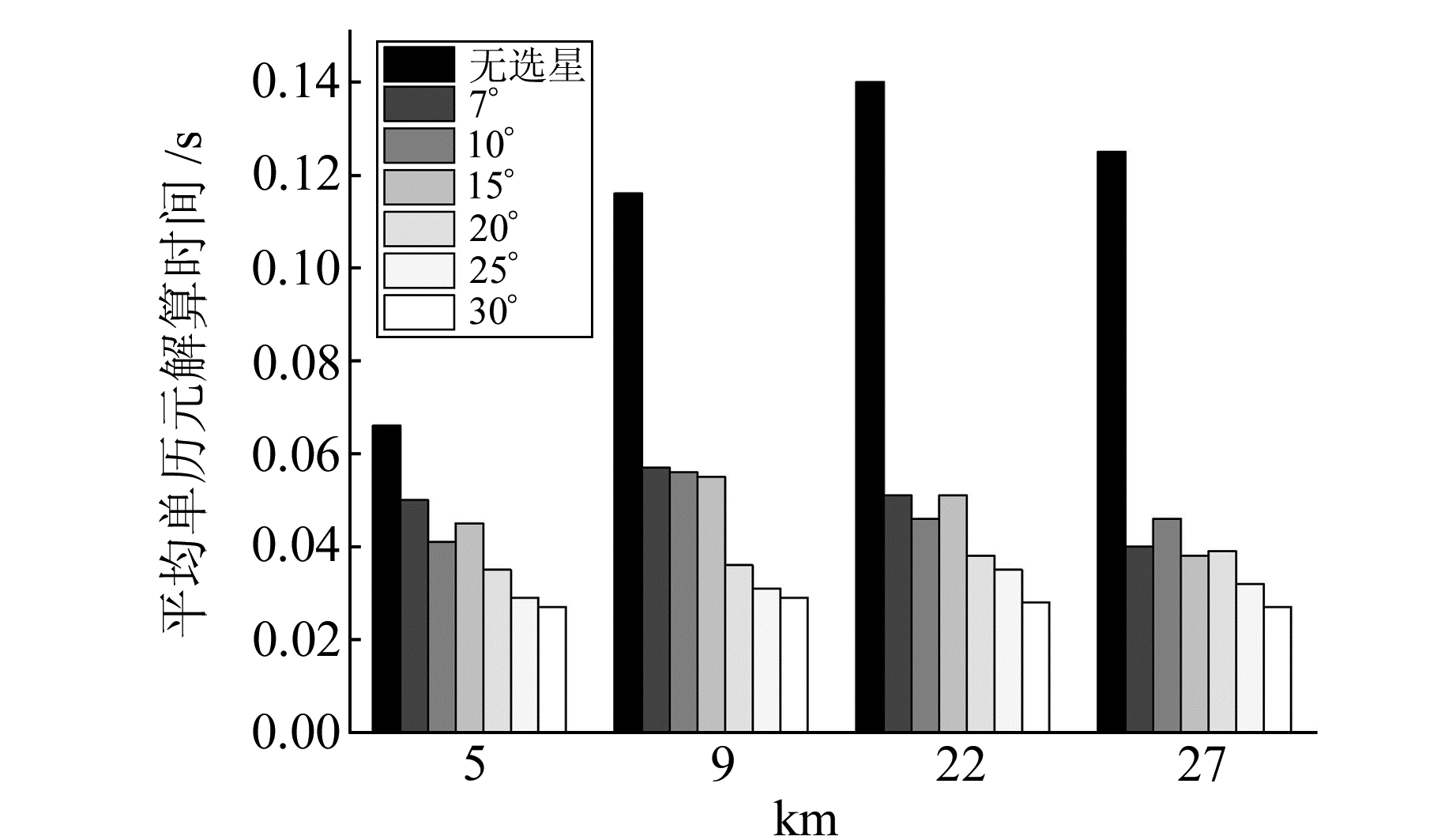
图 4 不同长度基线各高度角阈值平均单历元解算时间 Fig. 4 The average single epoch resolution time of the elevation angle at different baselines |
从表 1可见,随着高度角阈值增加,可视卫星数缓慢减少至10颗左右。从图 1~4可见,随着高度角阈值增大,虽然卫星数减少,但因低高度角卫星观测值被剔除,定位精度并未明显降低。高度角阈值为15°时解算精度和原始精度十分接近; 为25°时,解算精度不但与原始精度相当甚至有所提升,在U方向尤为明显; 为30°时,由于卫星数变少,高程定位精度降低。整体而言,当高度角阈值增加到25°时,解算效率提升70%以上。需要说明的是,图 3中5 km短基线的高程精度显著差于更长基线,主要是由于算例中5 km短基线的高差为160 m,其对流层延迟误差较大,且主要作用于高程方向,难以通过双差手段消除,而其他基线的高差分别为30 m、44 m、60 m,差分结果较为理想。实验表明,在亚太区域高度角阈值为25°时精度与效率达到近似平衡,所以下文中改进六星法高度角阈值均设置为25°。
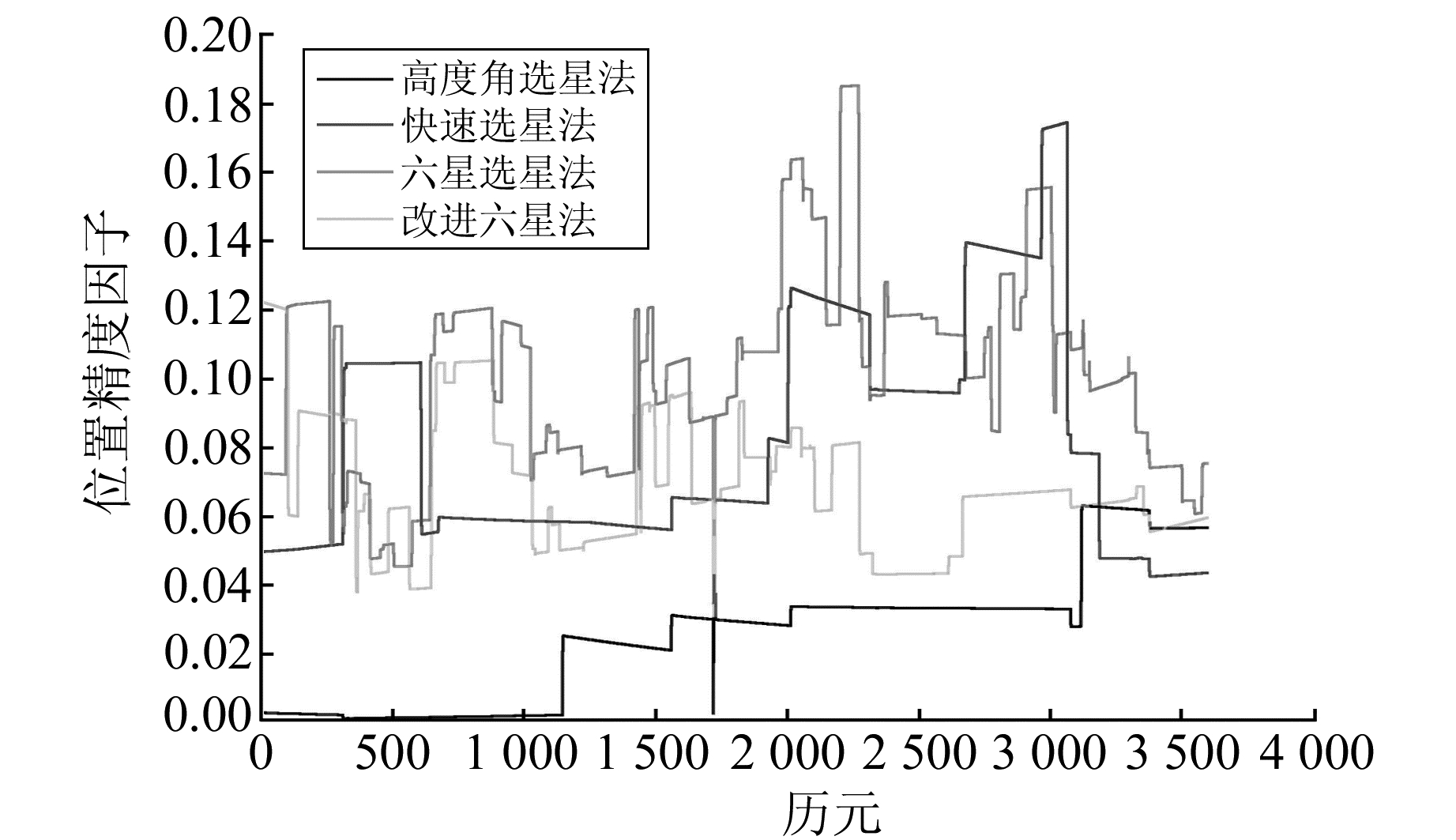
2.2 不同选星方法适用性分析为验证高度角阈值的合理性和精度,并分析改进六星法相对于其他选星方法在精度和效率方面的优势,采用常规六星选星法、高度角选星法、基于高度角和方位角的快速选星法分别进行数据处理,并与改进六星法进行对比。选取西安泾阳一短基线观测数据,基线长度300 m。分别采用不同选星方法进行BDS/GPS组合实时动态定位解算,观测时间为2016-8-28 00:04~00:05,数据采样率为1 s。4种方法的PDOP如图 5,定位精度如图 6,解算时间如图 7。
|
图 5 4种方法选星后的PDOP差异 Fig. 5 PDOP differences of four satellite selection algorithms |
|
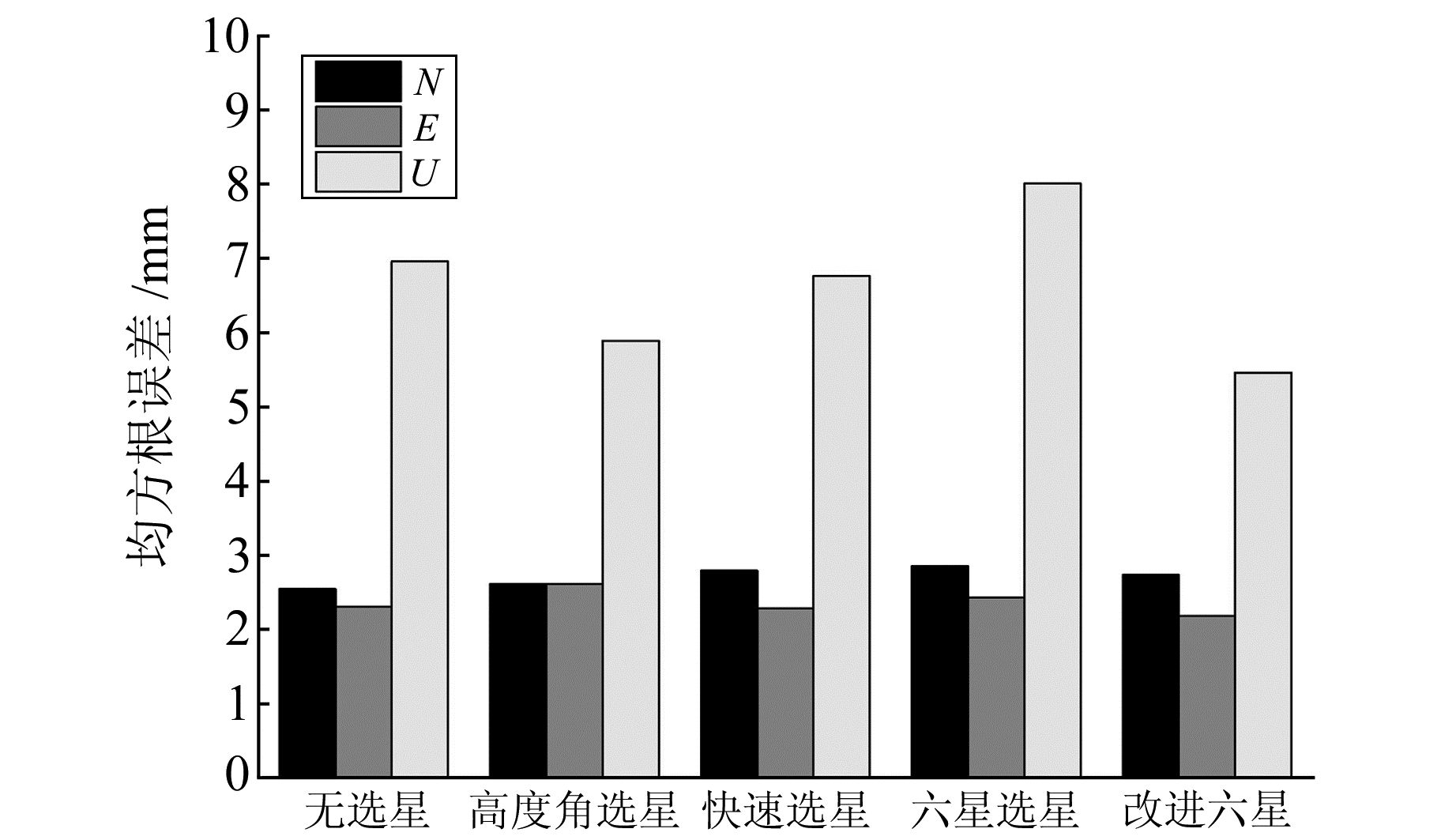
图 6 不同选星方法定位精度 Fig. 6 The positioning accuracy of different satellite selection algorithms |
|
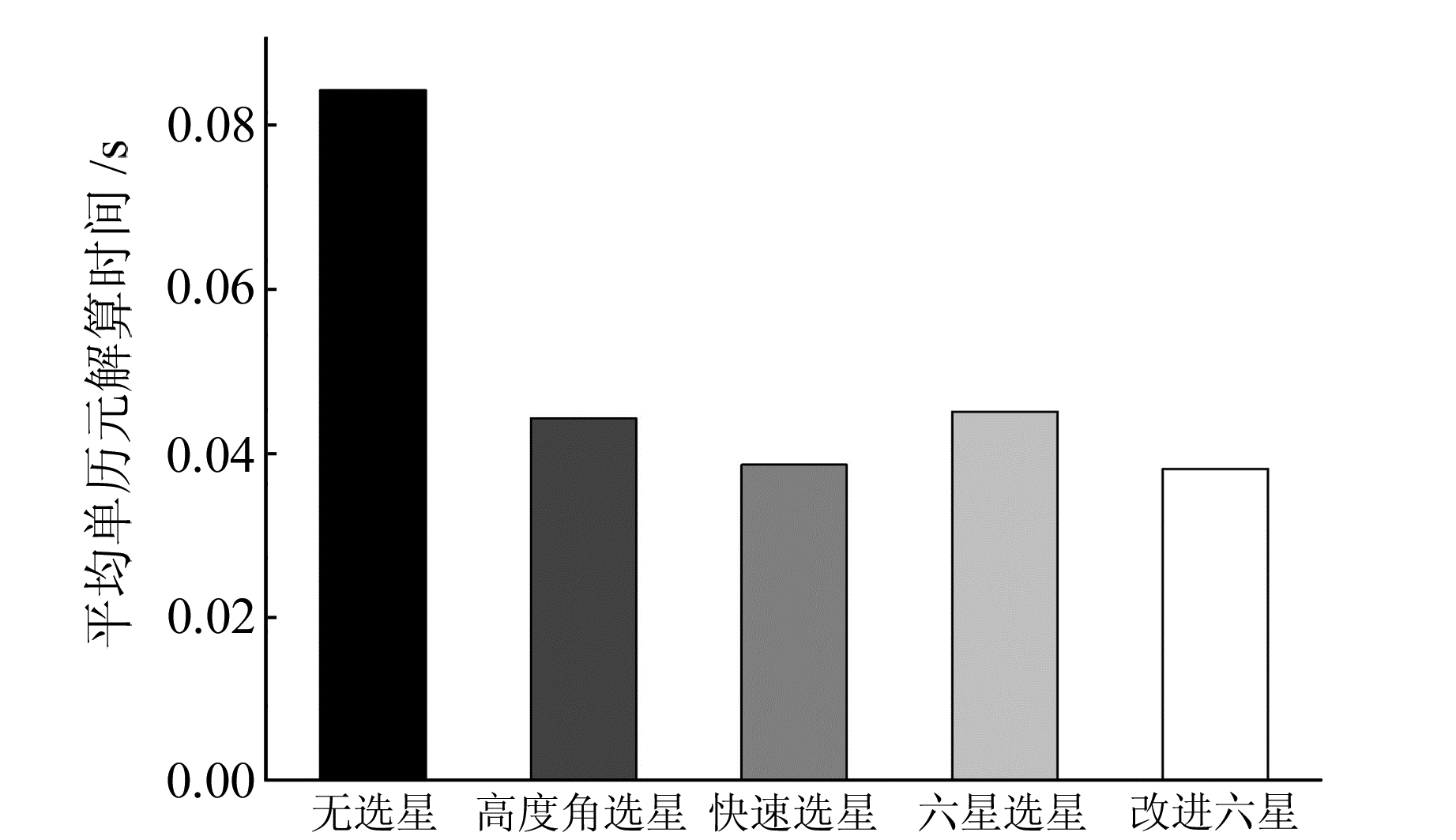
图 7 不同选星方法解算时间 Fig. 7 The time of solution for different satellite selection algorithms |
从图 5可见,采用高度角选星时,卫星数较多,PDOP也最小; 其他3种方法所选卫星构型相似,PDOP相近,但改进六星法最小。图 6中,六星选星法和快速选星法由于要选一颗高度角最低的卫星,所以精度相比未选星时有所降低; 而改进六星法和高度角选星法删除了低高度角卫星,大大减弱了观测值残差,定位精度较好。图 7中,4种选星方法都能大幅降低解算时间,运算效率提升50%以上,其中改进六星法效果最好。
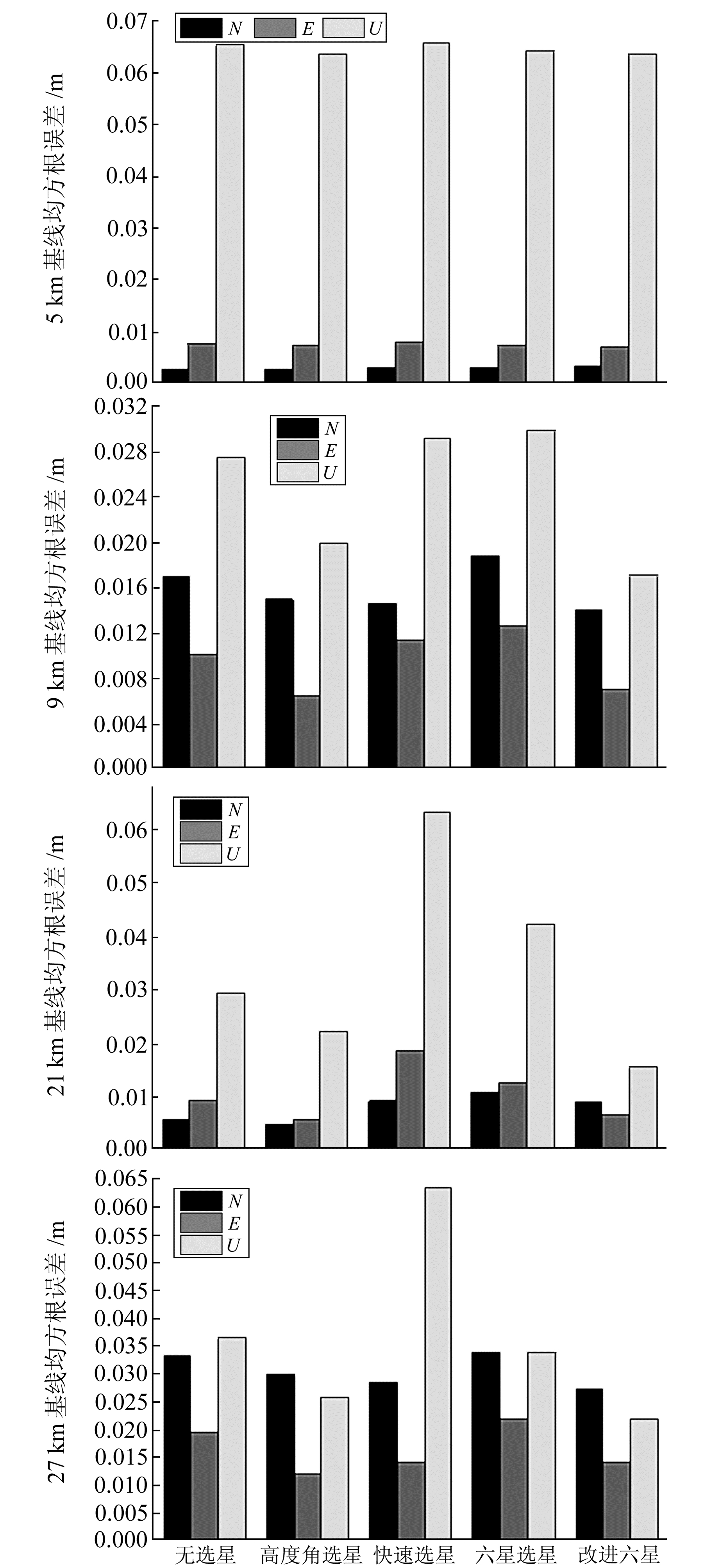
为验证改进六星法在不同基线长度下的定位适用性,利用上节5 km、9 km、22 km、27 km等4条基线观测数据,分别采用4种选星算法进行BDS/GPS联合RTK实时动态解算。4种选星方法的精度对比和计算时间如图 8和9所示。
|
图 8 4种选星方法在不同长度基线下的精度对比 Fig. 8 The accuracy comparison of four kinds of satellite selection algorithm at different baselines |
|
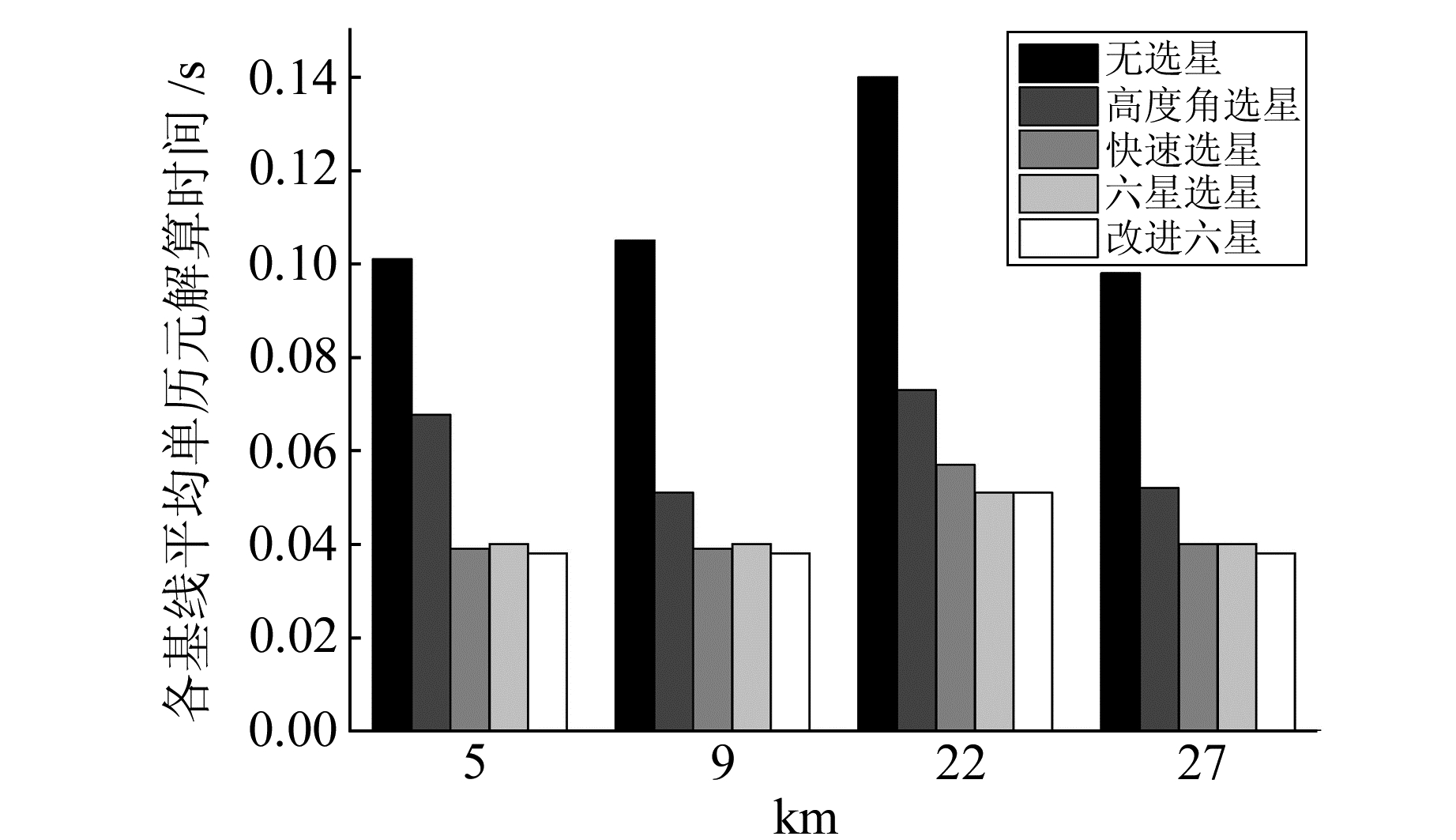
图 9 4种选星方法在不同长度基线下的解算时间对比 Fig. 9 The time comparison of four kinds of satellite selection algorithm at different baselines |
从图 8可以看出,在不同长度基线中,改进六星法相比其他几种选星算法精度更加接近甚至优于原始精度,尤其在高程方向,定位精度可提升40%左右。从图 9可以看出,对于不同长度基线,快速选星法、六星选星法和改进六星法的解算时间非常接近,但改进六星法略微占优。
3 结语本文针对传统选星方法的不足,提出顾及高度角阈值的改进六星选星法,能有效减弱低高度角卫星对BDS/GPS组合定位的影响,在保证不损失定位精度的前提下,显著提升解算效率。另外,本文提出的改进六星选星法同样适用于其他模式GNSS实时组合定位。
| [1] |
王双喜, 许坚. 精密GPS实时动态定位(RTK)中卫星的选择[J]. 测绘与空间地理信息, 2004, 27(5): 66-68 (Wang Shuangxi, Xu Jian. The Selection of Satellite in Precise GPS-RTK Positioning[J]. Geomatics & Spatial Information Technology, 2004, 27(5): 66-68)
(  0) 0) |
| [2] |
丛丽, Abidat A I, 谈展中. 卫星导航几何因子的分析和仿真[J]. 电子学报, 2006, 34(12): 2204-2208 (Cong Li, Abidat A I, Tan Zhanzhong. Analysis and Simulation of the GDOP Satellite Navigation[J]. Acta Electronica Sinica, 2006, 34(12): 2204-2208 DOI:10.3321/j.issn:0372-2112.2006.12.017)
(  0) 0) |
| [3] |
胡耀坤, 郑金华, 杨明. GPS/BD2高仰角选星组合差分精度分析[C]. 中国卫星导航学术年会, 西安, 2015 (Hu Yaokun, Zheng Jinhua, Yang Ming. The Precisions Analysis of Selected High Elevation Satellites for GPS/BD2 Combination Differential Positioning[C]. China Satellite Navigation Conference, Xi'an, 2015)
(  0) 0) |
| [4] |
张超, 陈天麒. GPS中的一种新的选星方法[J]. 实验科学与技术, 2006, 4(2): 25-27 (Zhang Chao, Chen Tianqi. A New Selecting-Star Algorithm in GPS[J]. Experiment Science and Technology, 2006, 4(2): 25-27)
(  0) 0) |
| [5] |
吴瑞祥, 蔡体菁. 基于高度角和方位角的选星方法[J]. 舰船电子工程, 2009, 29(11): 73-75 (Wu Ruixiang, Cai Tijing. An Satellites Selection Algorithm Bsaed on Elevation and Azimuth[J]. Ship Electronic Engineering, 2009, 29(11): 73-75 DOI:10.3969/j.issn.1627-9730.2009.11.020)
(  0) 0) |
| [6] |
高星伟, 过静珺, 程鹏飞, 等. 基于时空系统统一的北斗与GPS融合定位[J]. 测绘学报, 2012, 41(5): 743-748 (Gao Xingwei, Guo Jingjun, Cheng Pengfei, et al. Fusion Positioning of Beidou/GPS Based on Spatio Temporal System Unification[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 743-748)
(  0) 0) |
| [7] |
Teunissen P J G. The Least-Squares Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy, 1995, 70(1): 65-82
(  0) 0) |
| [8] |
袁建平, 罗建军, 岳晓奎, 等. 卫星导航原理与应用[M]. 北京: 中国宇航出版社, 2003 (Yuan Jianping, Luo Jianjun, Yue Xiaokui, et al. Satellite Navigation System: Principle and Application[M]. Beijing: China Astronautic Publishing House, 2003)
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38


