随着GNSS、InSAR等大地测量技术的发展,进行地球物理大地测量反演的数据源越来越丰富。许多学者采用非线性的智能优化算法进行反演并取得较好成果。何飞等[1]利用一维遗传算法反演等离子体层密度误差小于8%,陈华根等[2]运用模拟退火算法解决MT-重力联合反演的问题,王帅等[3]对粒子群算法收敛性和收敛速度加以改进,并用于反演断层滑动速率问题。上述研究在处理反演问题时均未考虑数据源存在粗差的情况。在大地测量与地球物理反演问题中,所使用的地面观测点的同震位移属于周围多断层的耦合响应而非单一断层的独立响应,同震位移并非理论上的同震位移,这是一种模型与观测值不匹配导致的“粗差”,而这类“粗差”更不易被发现[4]。图像自动匹配是实现摄影测量与遥感自动化处理的关键技术之一,RANSAC算法结合SIFT算子、SURF算子可提高遥感图像匹配的正确率[5-7]。本文将RANSAC算法和PSO算法相结合,剔除模拟数据中粗差点反演位错模型滑动参数,并以芦山地震为例加以验证。
1 RANSAC-PSO算法原理 1.1 粒子群算法原理粒子群算法(particle swarm optimization, PSO)是一种群体演化算法。PSO在求解优化问题时,由n+1个粒子(鸟)组成的群体对Q维空间中的目标点(食物)进行飞行搜索。每个粒子表示为xi=(xi1, xi2, xi3…xin),速度表示为vi=(vi1, vi2, vi3…vin)。影响粒子位置和速度变化的因素有粒子自身的历史最优值pi=(pi1, pi2, pi3…piQ)(鸟的自我认知)和全局最优值pg=(pg1, pg2, pg3…pgQ)(鸟的社会认知)[6-9]。粒子的位置和速度按式(1)、式(2)进行更新:
| $ v_{id}^{k + 1} = wv_{id}^k + {c_1}\varepsilon (p_{id}^k - x_{id}^k) + {c_2}\eta (p_{id}^k - x_{id}^k) $ | (1) |
| $ x_{id}^{k + 1} = x_{id}^k + rv_{id}^{k + 1} $ | (2) |
式中,w为粒子保持自身速度的惯性权重,c1、c2分别为跟踪自己历史最优值的权重和跟踪全局最优值的权重,ε、η为[0, 1]的随机数。
1.2 随机抽样一致性算法原理RANSAC(random sample consensus)算法是通过迭代从一组含有异常值(粗差)的数据中估计模型参数的方法[10-11]。RANSAC将数据假设为两类:内部值和异常值,随机地在数据中抽取样本来估计模型参数,并假设为正确的参数,以此判断其他的数据是否为内部值,然后重新估计模型参数。反复迭代,选取内部点最多的估计参数作为最优模型参数。
1.3 RANSAC-PSO算法流程| $ {\rm{min}}\varphi \left( p \right) = \sum\limits_{j = 1}^n {{{\left[ {{u_j}\left( p \right) - {u_j}\left( o \right)} \right]}^2}} $ | (3) |
式中,n为观测值个数,uj(p)为Okada模型计算结果,uj(o)为大地测量观测值。类似最小二乘原理构造的目标函数,当只存在偶然误差时,在统计学上表现出无偏性、有效性、一致性。但实际情况中又不可避免地存在粗差点:大地测量观测值不可能是实际的同震形变;断层的分段与实际情况不完全一致,导致数据与模型不匹配;由于地质原因导致有些地区位移异常。粗差的存在会导致minφ(p)发生突变,PSO反演的断层滑动参数U1、U2、U3发生偏差。所以,在进行断层滑动参数反演时对大地测量数据进行粗差定位和剔除很有必要。
本文将PSO算法和RANSAC算法相结合,对大地测量数据进行粗差定位和剔除,从而提高反演参数的精度。算法流程如下:
1) 确定反演必要的最小样本个数(sample),随机抽取最小样本;
2) 对最小样本使用PSO反演Okada滑动参数U10、U20、U30;
3) 假设U10、U20、U30为最优参数,使用Okada模型计算uj(p);
4) 计算φ(p)j=[uj(p)-uj(o)]2并与数据误差阈值(threshError)比较,小于阈值的数据定义为内部值并记录其个数(Num);
5) 判断Num是否大于内部值个数阈值(inlierNum),如果大于则Num替换inlierNum并重新反演参数U11、U21、U31,定义其为bestparameter;
6) 反复迭代,确定bestparameter作为最后结果。
2 模拟实验为了验证RANSAC算法与PSO算法结合能有效定位和剔除粗差从而提高反演参数精度,本文模拟断层模型,断层参数如表 1所示。
|
|
表 1 断层参数 Tab. 1 Parameters of fault |
在表 1断层参数的基础上,在断层中心10 km×10 km的区域均匀构造10×10个地面点,先利用Okada模型[14]计算地面点的理论值,然后加入数学期望为0、方差为3的随机噪声模拟地面观测值,最后人为加入1%、5%、10%的粗差作为实际观测值。
分别采用PSO、选权迭代法和RANSAC-PSO对实际观测值进行Okada模型的U1、U2、U3参数反演。RANSAC-PSO反演的流程与参数选取如下:首先需要确定最小样本数sample的值,即求解断层滑动参数U10、U20、U30的最小方程组个数是3。在模拟的实际观测值中抽取3个数据,利用PSO反演断层滑动参数U10、U20、U30,利用U10、U20、U30计算相应点uj(p)。在进行下一步之前,需根据实际情况计算数据误差阈值(threshError)。参考汶川同震GPS观测数据,给出GPS点位在N、E方向上的误差δ在3 mm左右。根据误差传播定律计算φ(p)=[uj(p)-uj(o)]2的δφ(p)2为9,不含粗差情况下数据呈正态分布,应符合3δ原则,φ(p)小于27,所以选定threshError为27,φ(p)小于27的点即为内部值(inliers),并记录个数(Num)。最后将Num与内部值个数阈值(inlierNum)比较,若大于inlierNum,inlierNum值将被Num替换,利用得到的内部值反演断层滑动参数U11、U21、U31并定义为最优参数bestparameter,替换后可保证U11、U21、U31与更多的点位匹配。实践中粗差率一般在10%以内,内部值个数阈值(inlierNum)初值为80个。反复迭代得到bestparameter,结果如表 2所示。
|
|
表 2 断层参数反演结果 Tab. 2 Inversion results of fault sliding |

|
图 1 各区间误差所占百分比 Fig. 1 Percentage of error within each interval |
从表 2可以看出,PSO随着粗差率增大,U1、U2、U3参数反演精度逐渐降低。选权迭代虽然具有一定的抗差能力,但当粗差为10%时,U1、U2、U3参数反演精度比单纯采用PSO精度差。RANSAC-PSO随粗差率增大,U1、U2、U3参数反演精度变化不大。
在单个粗差情况下,PSO与RANSAC-PSO反演的U1、U2、U3参数近似,由反演参数计算的地面点位移值误差不超过4 mm。在粗差率达到5%、10%时,PSO与RANSAC-PSO反演的U1、U2、U3参数相差达到cm级、dm级,由PSO反演参数计算出的地面点误差超过4 mm的点占41.05%、75.56% (除去粗差点之外),而由RANSAC-PSO反演参数计算出的地面点误差均未超过4 mm。
当粗差率为5%时,由选权迭代法反演参数计算出的地面点误差超过4 mm的点占18.95%(除去粗差点之外),优于单纯PSO。当粗差率为10%时,由选权迭代法反演参数计算出的地面点误差超过4 mm的点占78.89%(除去粗差点之外),劣于单纯PSO,抗差能力受到破坏,与RANSAC-PSO相比其稳定性差。
3 RANSAC-PSO反演芦山断层滑动速率为了验证RANSAC-PSO在实际中的应用,以芦山地震为例反演断层的滑动速率,断层几何模型采用许才军[15]的模型A,此模型基准点为断层中心,具体参数如表 3所示。
|
|
表 3 芦山断层参数 Tab. 3 Parameters of Lushan fault |
反演所用的数据为Jiang等[16]给出的33个GPS同震位移点,分别使用PSO和RANSAC-PSO反演芦山断层的滑动速率。PSO反演芦山断层U1为0.019 8 m、U2为0.690 8 m,释放能量8.396 0×1018 N ·m(MW 6.58);RANSAC-PSO反演芦山断层U1为0.051 8 m、U2为0.828 9 m,释放能量1.000 9×1019 N ·m(MW 6.63级),与GCMT计算的释放能量1.060 0×1019 N ·m更加吻合。反演结果均表明芦山为明显的逆冲断层,与实际情况相符。
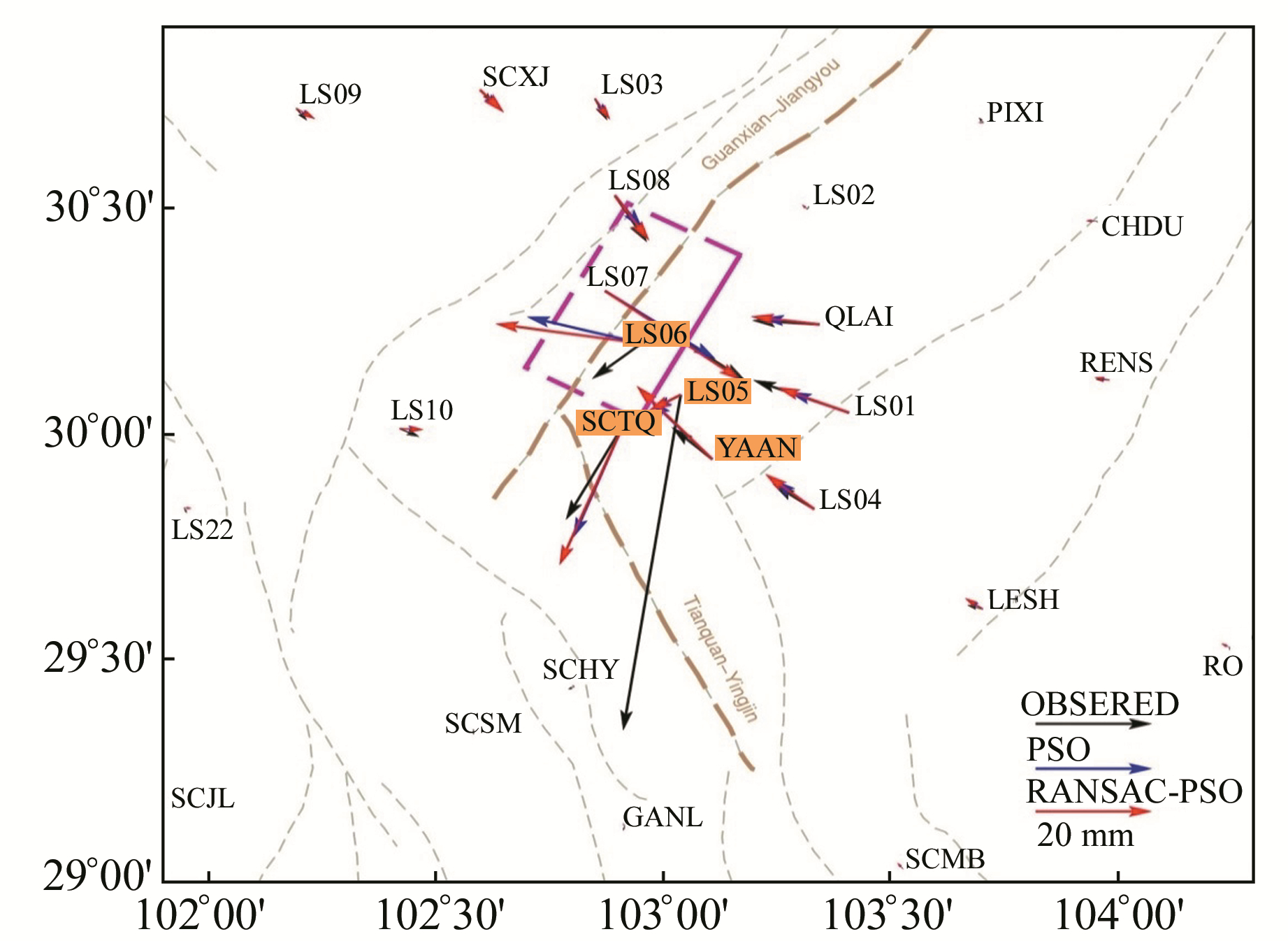
由图 2可知,与PSO相比,利用RANSAC-PSO反演所得滑动参数计算的地表水平位移整体上更接近GPS观测值。在断层近场区域内LS01、LS03、LS07、LS08、QLAI五个点上,RANSAC-PSO均优于PSO(表 4)。
|
图 2 GPS同震位移观测值、PSO计算值、RANSAC-PSO计算值 Fig. 2 Coseismic displacements observations and predicted by PSO and RANSAC-PSO |
|
|
表 4 PSO与RANSAC-PSO近场同震位移比较 Tab. 4 PSO and RANSAC-PSO comparisons in near field |
在SCTQ、LS05、LS06、YAAN四个点上,PSO和RANSAC-PSO反演结果与GPS观测值的拟合程度都不太理想, 其中SCTQ、YAAN点RANSAC-PSO计算结果与PSO计算结果相比稍大,但两者在方向上一致;LS05点PSO与RANSAC-PSO计算结果与观测值相比均过小;LS06点RANSAC-PSO结果比PSO在方向上更接近观测值,但RANSAC-PSO能够有效地判断出SCTQ、LS05、LS06、YAAN会对反演结果产生影响。
4 讨论与认识RANSAC-PSO中选取threshError、inlierNum初值非常重要,threshError过大会导致内部值的判断不准而使反演结果错误,过小则导致利用数据不充分;若inlierNum初值过小,则执行RANSAC-PSO第5步反演的次数增多而降低了效率,过大则可能无法得到反演结果。在RANSAC中sample是确定模型的必要值,为定值,而在使用RANSAC-PSO反演时sample值则与粗差率有关。本文中RANSAC-PSO将最小样本个数(sample)设为定值3。
RANSAC-PSO具有稳健性高的特点,当粗差率为10%、迭代次数为5时,RANSAC-PSO得到正确结果的概率为98.84%,且多次重复实验最终结果变化小于0.1 mm。粗差达10%时,PSO算法反演的滑动参数与理论值相差23.2 cm,选权迭代法反演的滑动参数与理论值相差26.2 cm,而RANSAC-PSO反演的滑动参数与理论值相差小于1 cm。
在正演芦山地震的同震位移时,在SCTQ、LS05、LS06、YAAN四个点上,RANSAC-PSO和PSO的计算结果与GPS观测值差异较大,其主要原因可能为这4点位于灌县-江油断层与天全-荥经断层的交界处,地表观测点的位移不单单是由芦山断层的滑动引起。尤其是LS05点,GPS观测值E分量为-9.9 mm,N分量为-66.8 mm;而PSO与RANSAC-PSO计算的E分量分别为-4.7 mm、-5.6 mm,N分量分别为-3 mm、-3.3 mm,后两者在N分量明显小于GPS观测,该差异可能是地震滑脱导致的结果。另外,芦山断层的滑动本身是不均匀的,采用单一断层不能准确描述断层的滑动分布,点LS07、点LS01的GPS观测和正算结果均说明芦山断层滑动速率北段大于南段且具有逆冲特征。芦山震例表明,与PSO相比,RANSAC-PSO反演的滑动速率更接近实际;RANSAC-PSO正演结果与PSO在远场一致,在近场点LS01、LS03、LS07、LS08、QLAI优于PSO。
| [1] |
何飞, 张效信, 陈波, 等. 遗传算法反演地球等离子体层离子密度分布[J]. 地球物理学报, 2012, 55(1): 29-35 (He Fei, Zhang Xiaoxin, Chen Bo, et al. Inversion of the Earth's Plasmaspheric Desity Distribution from EUV Images with Genetic Algorithm[J]. Chinese Journal of Geophysics, 2012, 55(1): 29-35)
(  0) 0) |
| [2] |
陈华根, 李嘉虓, 吴健生, 等. MT-重力模拟退火联合反演研究[J]. 地球物理学报, 2012, 55(2): 663-670 (Chen Huagen, Li Jiaxiao, Wu Jiansheng, et al. Study on Simulated-Annealing MT-Gravity Joint Inversion[J]. Chinese Journal of Geophysics, 2012, 55(2): 663-670)
(  0) 0) |
| [3] |
王帅, 张永志, 姜永涛, 等. 维多样性的动态权重粒子群算法反演断层滑动速率[J]. 地球物理学进展, 2014(4): 1766-1771 (Wang Shuai, Zhang Yongzhi, Jiang Yongtao, et al. Slip Velocity of Fault Induced by PSO Algorithm with Dynamical Inertial Weight and Dimension Mutation[J]. Progress in Geophysics, 2014(4): 1766-1771)
(  0) 0) |
| [4] |
许才军. 地球物理大地测量反演理论与应用[M]. 武汉: 武汉大学出版社, 2015 (Xu Caijun. Joint Inversion Theory Geophysics and Geodesy and It's Application[M]. Wuhan: Wuhan University Press, 2015)
(  0) 0) |
| [5] |
赵烨, 蒋建国, 洪日昌. 基于RANSAC的SIFT匹配优化[J]. 光电工程, 2014(8): 58-65 (Zhao Ye, Jiang Jianguo, Hong Richang. An Optimized SIFT Matching Based on RANSAC[J]. Opto-Electronic Engineering, 2014(8): 58-65)
(  0) 0) |
| [6] |
陈艺虾, 孙权森, 徐焕宇, 等. SURF算法和RANSAC算法相结合的遥感图像匹配方法[J]. 计算机科学与探索, 2012(9): 822-828 (Chen Yixia, Sun Quansen, Xu Huanyu, et al. Matching Method of Remote Sensing Images Based on SURF Algorithm and RANSAC Algorithm[J]. Journal of Frontiers of Computer Science and Technology, 2012(9): 822-828)
(  0) 0) |
| [7] |
李德仁, 袁修孝. 误差处理与可靠性理论[M]. 武汉: 武汉大学出版社, 2012 (Li Deren, Yuan Xiuxiao. Error Processing and Reliability Theory[M]. Wuhan: Wuhan University Press, 2012)
(  0) 0) |
| [8] |
黄少荣. 粒子群优化算法综述[J]. 计算机工程与设计, 2009(8): 1977-1980 (Huang Shaorong. Survey of Particle Swarm Optimization Algorithm[J]. Computer Engineering and Design, 2009(8): 1977-1980)
(  0) 0) |
| [9] |
杨维, 李歧强. 粒子群优化算法综述[J]. 中国工程科学, 2004(5): 87-94 (Yang Wei, Li Qiqiang. Survey on Particle Swarm Optimization Algorithm[J]. Engineering Science, 2004(5): 87-94)
(  0) 0) |
| [10] |
Zhang Y, Wang S, Ji G. A Comprehensive Survey on Particle Swarm Optimization Algorithm and Its Applications[J]. Mathematical Problems in Engineering, 2015(1): 1-38
(  0) 0) |
| [11] |
Shen L C, Huo X H, Niu Y F. Survey of Discrete Particle Swarm Optimization Algorithm[J]. Systems Engineering & Electronics, 2008, 30(10): 1986-1952
(  0) 0) |
| [12] |
Hast A, Nysjö J, Marchetti A. Optimal RANSAC-Towards a Repeatable Algorithm for Finding the Optimal Set[J]. Journal of Wscg, 2013, 21(1): 21-30
(  0) 0) |
| [13] |
Choi S, Kim T, Yu W. Performance Evaluation of RANSAC Family[C]. DBLP, London, 2009
(  0) 0) |
| [14] |
张永志, 徐海军, 王卫东, 等. 渭河盆地断裂活动速率的粒子群算法反演[J]. 西北地震学报, 2011(4): 322-325 (Zhang Yongzhi, Xu Haijun, Wang Weidong, et al. Inversion on Slip Velocity of Main Faults in Weihe Basin by Particle Swarm Optimization Algorithm with GPS Data[J]. Northwestern Seismological Journal, 2011(4): 322-325)
(  0) 0) |
| [15] |
段虎荣, 张永志, 徐海军. 改进的粒子群算法在断层滑动速率反演中的应用[J]. 大地测量与地球动力学, 2011(6): 31-36 (Duan Hurong, Zhang Yongzhi, Xu Haijun. Improved Particle Swarm Optimization Algorithm and It's Application in Inversion of Slip Velocity of Fault[J]. Journal of Geodesy and Geodynamics, 2011(6): 31-36)
(  0) 0) |
| [16] |
Okada Y. SurfaceDeformation Due to Shear and Tensile Faults in a Half-Space[J]. Bulletin of the Seismological Society of America, 1985, 92(2): 1018-1040
(  0) 0) |
| [17] |
许才军, 周力璇, 尹智. 2013年MS 7.0级中国芦山地震断层曲面模型的构建及其滑动分布的大地测量反演[J]. 武汉大学学报:信息科学版, 2017, 42(11): 1165-1671 (Xu Caijun, Zhou Lixuan, Yin Zhi. Construction and Geodesy Slip Inversion Analysis of 2013 Ms7.0 Lushan in China Earthquake's Curved Fault Modle[J]. Geomatics and Information Science of Wuhan University, 2017, 42(11): 1165-1671)
(  0) 0) |
| [18] |
Jiang Z, Wang M, Wang Y, et al. GPS Constrained Coseismic Source and Slip Distribution of the 2013 MW6.6 Lushan, China, Earthquake and Its Tectonic Implications[J]. Geophysical Research Letters, 2014, 41(2): 407-413 DOI:10.1002/2013GL058812
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38

