2. 武汉市测绘研究院博士后创新实践基地,武汉市万松园路209号,430022;
3. 东华理工大学江西省数字国土重点实验室,南昌市广兰大道418号,330013;
4. 武汉大学测绘学院,武汉市珞喻路129号,430079;
5. 武汉光谷北斗控股集团有限公司,武汉市光谷七路130号,430206
三维激光扫描虽然没有传统的GNSS或全站仪单点监测手段精度高[1],但可以获取区域点云数据,并最终实现对区域整体的监测,同时可通过密集点云实现对地面监测区域细节的描述[2],已经在灾害监测中得到广泛应用[3]。利用三维激光扫描对井架进行扫描,并通过特征点对比分析可实现井架倾斜变形监测[4];通过边坡点云对比分析可实现滑坡区域及滑坡量的提取[5];利用远距离的三维激光扫描仪对跨海大桥进行扫描,并通过分析大桥柱端点云变化量可实现跨海大桥变形的监测,结果显示三维激光扫描监测结果误差不超过0.5 mm[6]。
以上方法虽然可以实现三维激光扫描的变形监测,但其对监测结果的可靠性没有进行评价,即对于得到的点云变化值是否反映真实变形没有指标进行评价。而由点云误差造成的不同期点云变化量达到cm级[7],而该误差可能掩盖住变形量,提取的变化量不能真实代表目标物的变形。因此,本文对激光扫描测距、测角及配准误差进行分析,利用信息熵和误差熵的关系,构建点云误差熵模型,并基于该模型实现点云变形可靠性评价指标的计算,最终通过滑坡监测实例确定该指标的有效性。
1 点云误差模型 1.1 点位误差模型三维激光在扫描过程中采集的是测距ρ、水平角θ和垂直角φ,而目标物的三维坐标是极坐标系统下的坐标[x y z],其与测距、测角的关系为:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_{{\rm{car}}}} = {{\left[ {\begin{array}{*{20}{c}} x&y&z \end{array}} \right]}^{\rm{T}}} = }\\ {{{\left[ {\begin{array}{*{20}{c}} {\rho \sin \theta \rm{\cos} \varphi }&{\rho \sin \theta \sin \varphi }&{\rho \rm{cos}\theta } \end{array}} \right]}^{\rm{T}}}} \end{array} $ | (1) |
仪器厂商提供的测距ρ、水平角θ和垂直角φ的标准差分别为σρ、σθ和σφ,而测距标准差σρ是在入射角为0的情况下给出的,实际扫描过程中入射角不可能为0。假设扫描过程中入射角为α,则任意入射角下的测距方差与入射角为0情况下测距方差关系为[8]:
| $ \sigma {'}_\rho ^2 = \frac{{\sigma _\rho ^2}}{{{{\cos }^2}\alpha }} $ | (2) |
根据误差传播规律,Pcar的协方差矩阵为:
| $ {\mathit{\boldsymbol{C}}_{{\rm{car}}}} = \left[ {\begin{array}{*{20}{c}} {\sigma _x^2}&{{\sigma _{xy}}}&{{\sigma _{xz}}}\\ {{\sigma _{xy}}}&{\sigma _y^2}&{{\sigma _{yz}}}\\ {{\sigma _{xz}}}&{{\sigma _{xz}}}&{\sigma _z^2} \end{array}} \right] = \mathit{\boldsymbol{K}}{\mathit{\boldsymbol{C}}_{{\rm{pol}}}}{\mathit{\boldsymbol{K}}^{\rm{T}}} $ | (3) |
式中,
| $ \mathit{\boldsymbol{K = }}\left[ {\begin{array}{*{20}{c}} {\frac{{\partial x}}{{\partial \rho }}}&{\frac{{\partial x}}{{\partial \theta }}}&{\frac{{\partial x}}{{\partial \varphi }}}\\ {\frac{{\partial y}}{{\partial \rho }}}&{\frac{{\partial y}}{{\partial \theta }}}&{\frac{{\partial y}}{{\partial \varphi }}}\\ {\frac{{\partial z}}{{\partial \rho }}}&{\frac{{\partial z}}{{\partial \theta }}}&{\frac{{\partial z}}{{\partial \varphi }}} \end{array}} \right],{\mathit{\boldsymbol{C}}_{{\rm{pol}}}} = {\rm{diag}}\left\{ {\sigma {'}_\rho ^2,\sigma _\theta ^2,\sigma _\varphi ^2} \right\}。$ |
三维激光扫描过程中,不同测站点云配准公式为:
| $ {\mathit{\boldsymbol{P}}_{\rm{g}}} = {\mathit{\boldsymbol{T}}_{{\rm{ig}}}} + {\mathit{\boldsymbol{R}}_{{\rm{ig}}}}{\mathit{\boldsymbol{P}}_{{\rm{car}}}} $ | (4) |
式中,Pg= [xg yg zg] T为全局坐标系统中的坐标, Tig= [Δx Δy Δz] T为坐标转换的平移向量, Rig是含有旋转角的旋转向量。
利用误差传播规律,Pg的协方差矩阵为:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{C}}_{{p_{\rm{g}}}}} = \left[ {\begin{array}{*{20}{c}} {\sigma _{{x_{\rm{g}}}}^2}&{{\sigma _{{x_{\rm{g}}}{y_{\rm{g}}}}}}&{{\sigma _{{x_{\rm{g}}}{z_{\rm{g}}}}}}\\ {{\sigma _{{x_{\rm{g}}}{y_{\rm{g}}}}}}&{\sigma _{{y_{\rm{g}}}}^2}&{{\sigma _{{y_{\rm{g}}}{z_{\rm{g}}}}}}\\ {{\sigma _{{x_{\rm{g}}}{z_{\rm{g}}}}}}&{{\sigma _{{y_{\rm{g}}}{z_{\rm{g}}}}}}&{\sigma _{{z_{\rm{g}}}}^2} \end{array}} \right] = }\\ {\mathit{\boldsymbol{J}}_p^{{\rm{jg}}}\mathit{\boldsymbol{C}}_p^{\rm{g}}{{\left( {\mathit{\boldsymbol{J}}_p^{{\rm{jg}}}} \right)}^{\rm{T}}} + {\mathit{\boldsymbol{R}}_{{\rm{ig}}}}{\mathit{\boldsymbol{C}}_{{\rm{car}}}}{{\left( {{\mathit{\boldsymbol{R}}_{{\rm{ig}}}}} \right)}^{\rm{T}}}} \end{array} $ | (5) |
式中,Cp=diag {σΔx2, σΔy2, σΔz2, σ2α1, σ2α2, σ2α3}是3个旋转角α1、α2、α3和3个平移量的协方差矩阵,Jpjg是对平移和旋转变量求导的雅克比矩阵。
2 点云误差熵模型目前,描述点位不确定性的方法主要是误差椭球,而误差椭球的缺点是尺度参数k不能确定,同时,在点位不服从正态分布的情况下,误差椭球将无法运用。基于此,本文利用信息熵的定义,将误差熵引入到点位不确定性的描述中,误差熵不存在尺度参数k的不确定性,可以唯一确定点位的不确定性大小,在正态分布情况下,误差熵与误差椭球存在相关性。
2.1 激光点误差椭球模型激光点位误差向量为pe=[δxg δyg δzg],则三维激光点的误差椭球形式为:
| $ \left[ {\begin{array}{*{20}{c}} {{\delta _{{x_{\rm{g}}}}}}&{{\delta _{{y_{\rm{g}}}}}}&{{\delta _{{z_{\rm{g}}}}}} \end{array}} \right]\mathit{\boldsymbol{C}}_{{p_{\rm{g}}}}^{ - {\rm{1}}}{\left[ {\begin{array}{*{20}{c}} {{\delta _{{x_{\rm{g}}}}}}&{{\delta _{{y_{\rm{g}}}}}}&{{\delta _{{z_{\rm{g}}}}}} \end{array}} \right]^{\rm{T}}} = {k^2} $ | (6) |
式中,k为尺度参数,将正交分解应用到对称矩阵Cpg-1中,则存在酉矩阵 Q满足QTCpgQ = Λ,Λ为对角矩阵Cpg的3个特征值,利用Q对测量点位误差椭球进行旋转和平移,得到标准化误差椭球模型:
| $ \frac{{{u^2}}}{{{\lambda _1}}} + \frac{{{v^2}}}{{{\lambda _2}}} + \frac{{{w^2}}}{{{\lambda _3}}} = {k^2} $ | (7) |
激光点位误差服从正态分布,其点位概率密度函数为:
| $ f\left( \mathit{\boldsymbol{r}} \right) = \frac{1}{{{{\left( {2{\rm{ \mathsf{ π} }}} \right)}^{\frac{3}{2}}}\sqrt {\left| {{\mathit{\boldsymbol{C}}_{{p_{\rm{g}}}}}} \right|} }}\exp \left\{ { - \frac{1}{2}\mathit{\boldsymbol{p}}_e^{\rm{T}}\mathit{\boldsymbol{C}}_{{p_{\rm{g}}}}^{ - {\rm{1}}}{\mathit{\boldsymbol{p}}_e}} \right\} $ | (8) |
将式(8)写为标准形式:
| $ \begin{array}{*{20}{c}} {f\left( {u,v,w} \right) = }\\ {\frac{1}{{{{\left( {2{\rm{ \mathsf{ π} }}} \right)}^{\frac{3}{2}}}\sqrt {{\lambda _1}{\lambda _2}{\lambda _3}} }}\exp \left\{ { - \frac{1}{2}\left( {\frac{{{u^2}}}{{{\lambda _1}}} + \frac{{{v^2}}}{{{\lambda _2}}} + \frac{{{w^2}}}{{{\lambda _3}}}} \right)} \right\}} \end{array} $ | (9) |
根据信息熵的定义[9], 激光点位信息熵为:
| $ P = - \int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {f\left( {u,v,w} \right)\ln f\left( {u,v,w} \right){\text{d}}u{\text{d}}v{\text{d}}w} } } $ | (10) |
定义
| $ u' = \frac{u}{{\sqrt {2{\lambda _1}} }},v' = \frac{v}{{\sqrt {2{\lambda _2}} }},w' = \frac{w}{{\sqrt {2{\lambda _3}} }} $ | (11) |
得到:
| $ \begin{array}{*{20}{c}} {P = \ln \left[ {{{\left( {2{{\rm{\pi }}}} \right)}^{\frac{3}{2}}}\sqrt {{\lambda _1}{\lambda _2}{\lambda _3}} } \right] + \frac{1}{{{{\rm{\pi }}^{\frac{3}{2}}}}}\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\left( {{{u'}^2} + {{v'}^2} + } \right.} } } } \\ {\left. {{{w'}^2}} \right)\exp \left\{ { - \left( {{{u'}^2} + {{v'}^2} + {{w'}^2}} \right)} \right\}{\text{d}}u'{\text{d}}v'{\text{d}}w'} \end{array} $ | (12) |
利用球面积分,式(12)变为:
| $ \begin{array}{*{20}{c}} {P = \ln \left[ {{{\left( {2{{\rm{\pi }}}} \right)}^{\frac{3}{2}}}\sqrt {{\lambda _1}{\lambda _2}{\lambda _3}} } \right] + } \\ {\frac{1}{{{{\rm{\pi }}^{\frac{3}{2}}}}}\iiint\limits_\Omega {{r^2}\exp \left\{ { - {r^2}} \right\}{r^2}\sin \omega {\text{d}}r{\text{d}}\omega {\text{d}}\psi }} \end{array} $ | (13) |
利用分步积分得到:
| $ \begin{array}{*{20}{c}} {P = \ln \left[ {{{\left( {2{\rm{ \mathsf{ π} }}} \right)}^{\frac{3}{2}}}\sqrt {{\lambda _1}{\lambda _2}{\lambda _3}} } \right] + \frac{4}{{\sqrt {\rm{ \mathsf{ π} }} }} \cdot }\\ {\frac{3}{4}\int\limits_0^{ + \infty } {\exp \left\{ { - {r^2}} \right\}{\rm{d}}r} = \ln \left[ {{{\left( {2{\rm{ \mathsf{ π} }}} \right)}^{\frac{3}{2}}}\sqrt {{\lambda _1}{\lambda _2}{\lambda _3}} } \right] + \frac{3}{2}} \end{array} $ | (14) |
根据误差熵和信息熵的关系,点位误差熵为:
| $ \begin{array}{*{20}{c}} {\Delta P = {{\rm{e}}^P} = {{\left( {2{\rm{ \mathsf{ π} }}} \right)}^{\frac{3}{2}}}\sqrt {{\lambda _1}{\lambda _2}{\lambda _3}} \cdot {{\rm{e}}^{\frac{3}{2}}} = }\\ {{{\left( {2{\rm{ \mathsf{ π} e}}} \right)}^{\frac{3}{2}}}\sqrt {{\lambda _1}{\lambda _2}{\lambda _3}} = {{\left( {2.564} \right)}^3}\frac{4}{3}{\rm{ \mathsf{ π} }}\sqrt {{\lambda _1}{\lambda _2}{\lambda _3}} } \end{array} $ | (15) |
由式(15)可知,在正态分布情况下,误差熵系数为[10]:
| $ k = {\left( {\frac{{\Delta P}}{{\frac{4}{3}{\rm{ \mathsf{ π} }}\sqrt {{\lambda _1}{\lambda _2}{\lambda _3}} }}} \right)^{\frac{1}{3}}} = 2.564 $ | (16) |
误差熵椭球的半长轴为2.564
假设相邻误差熵之间存在交集,为了得到比较准确的误差熵空间大小,需要对交集部分进行消除。假设在u方向存在交集,即
| $ \left\{ \begin{array}{l} \frac{{{u^2}}}{{a_i^2}} + \frac{{{v^2}}}{{b_i^2}} + \frac{{{w^2}}}{{c_i^2}} = 1\\ \frac{{{{\left( {u - d} \right)}^2}}}{{a_{i + 1}^2}} + \frac{{{v^2}}}{{b_{i + 1}^2}} + \frac{{{w^2}}}{{c_{i + 1}^2}} = 1 \end{array} \right. $ | (17) |
式中, d为扫描间隔,ai、bi和ci为u、v和w方向的误差熵椭球的半长轴长度,可以表示为ai=2.564
利用相邻误差熵重叠区域计算公式,得到相邻误差熵交集大小为:
| $ \begin{array}{*{20}{c}} {\Delta {p_{{\rm{overlap}}}} = \frac{2}{3}{\rm{ \mathsf{ π} }}{a_i}{b_i}{c_i} - {\rm{ \mathsf{ π} }}{b_i}{c_i}\left( {m - \frac{{{m^3}}}{{3a_i^2}}} \right) + }\\ {\frac{4}{3}{\rm{ \mathsf{ π} }}{a_{i + 1}}{b_{i + 1}}{c_{i + 1}} - {\rm{ \mathsf{ π} }}{b_{i + 1}}{c_{i + 1}}}\\ {\left[ {d + \frac{2}{3}{a_{i + 1}} - m + \frac{{{m^2}}}{{3a_{i + 1}^2}} + \frac{{m{d^2}}}{{a_{i + 1}^2}} - \frac{{{m^2}d}}{{a_{i + 1}^2}} - \frac{{{d^3}}}{{3a_{i + 1}^2}}} \right],}\\ {0 < d < {a_i} + {a_{i + 1}}} \end{array} $ | (18) |
式中,
| $ m = \left\{ \begin{array}{l} \frac{{ - a_i^2b_{i + 1}^2d + {a_i}{a_{i + 1}}\sqrt {a_i^2b_{i + 1}^4 - a_i^2b_i^2b_{i + 1}^2 + b_i^2b_{i + 1}^2{d^2} - a_{i + 1}^2b_i^2b_{i + 1}^2 + a_{i + 1}^2b_i^4} }}{{a_i^2b_{i + 1}^2 - a_{i + 1}^2b_i^2}},\frac{{{a_i}}}{{{a_{i + 1}}}} > \frac{{{b_i}}}{{{b_{i + 1}}}}\\ \frac{{ - a_i^2b_{i + 1}^2d - {a_i}{a_{i + 1}}\sqrt {a_i^2b_{i + 1}^4 - a_i^2b_i^2b_{i + 1}^2 + b_i^2b_{i + 1}^2{d^2} - a_{i + 1}^2b_i^2b_{i + 1}^2 + a_{i + 1}^2b_i^4} }}{{a_i^2b_{i + 1}^2 - a_{i + 1}^2b_i^2}},\frac{{{a_i}}}{{{a_{i + 1}}}} < \frac{{{b_i}}}{{{b_{i + 1}}}} \end{array} \right. $ |
假设有m行n列扫描点,u方向重叠区域数有(n-1)m个,则交集区域误差熵大小为:
| $ \Delta {P_{{\rm{overlap}}}} = \sum\limits_{i = 1}^{\left( {n - 1} \right)m} {\Delta {P_{{\rm{overlap}}}}} $ | (19) |
在不考虑相邻误差熵交集影响情况下,点云误差熵大小为:
| $ \Delta {P_{{\rm{entropy}}}} = \frac{4}{3}{\rm{ \mathsf{ π} }}\sum\limits_{i = 1}^{nm} {{a_i}{b_i}{c_i}} $ | (20) |
因此,实际点云误差熵为:
| $ \begin{array}{*{20}{c}} {\Delta {P_{{\rm{entropy}}}} = \Delta {P_{{\rm{entropy}}}} - \Delta {P_{{\rm{overlap}}}} = }\\ {\frac{4}{3}{\rm{ \mathsf{ π} }}\sum\limits_{i = 1}^{nm} {{a_i}{b_i}{c_i}} - \sum\limits_{i = 1}^{\left( {n - 1} \right)m} {\Delta {P_{{\rm{overlap}}}}} } \end{array} $ | (21) |
根据以上原理,利用相似的方法计算在v和w方向存在交集情况下的点云误差熵。
3 变形可靠性评价指标激光点位误差熵存在着3个半长轴,即代表误差区间的最大值方向。假设实际点位误差熵u、v和w方向半长轴为a′i、b′i和c′i,则实际点云误差熵表示为:
| $ \Delta {P_{{\rm{entropy}}}} = \frac{4}{3}{\rm{ \mathsf{ π} }}\sum\limits_{i = 1}^{nm} {\left( {{{a'}_i}} \right)\left( {{{b'}_i}} \right)\left( {{{c'}_i}} \right)} $ | (22) |
在不考虑相邻误差熵交集的情况下的误差熵为ΔPentropy,ΔPentropy与Δpentropy之间存在着缩放系数η,即
| $ {{a'}_i} = \eta {a_i},{{b'}_i} = \eta {b_i},{{c'}_i} = \eta {c_i} $ | (23) |
实际点云误差熵为:
| $ \Delta {P_{{\rm{entropy}}}} = \frac{4}{3}{\rm{ \mathsf{ π} }}\sum\limits_{i = 1}^{nm} {\left( {\eta {a_i}} \right)\left( {\eta {b_i}} \right)\left( {\eta {c_i}} \right)} $ | (24) |
由式(22)和(24), 得到:
| $ \eta = {\left( {\frac{{\Delta {P_{{\rm{entropy}}}}}}{{\Delta {P_{{\rm{entropy}}}}}}} \right)^{\frac{1}{3}}} $ | (25) |
从而有:
| $ {{a'}_i} = {\left( {\frac{{\Delta {P_{{\rm{entropy}}}}}}{{\Delta {P_{{\rm{entropy}}}}}}} \right)^{\frac{1}{3}}}{a_i} $ | (26) |
式中,a′i为误差熵半长轴的最长值,即激光点位误差不可能超过该值,从而可将该值作为变形可靠性评价指标,只有当变形大于该值时,提取的变形量才是可靠的变形。
4 实例分析利用Riegl-VZ400扫描仪对某个边坡进行不同时期的扫描,同时对控制点上的标靶进行扫描,利用标靶点云数据实现不同期点云的配准,如图 1所示。首先对整个区域进行粗扫,然后对边坡进行精扫,精扫过程设置的扫描间隔为8 mm。扫描日期分别为2016-10-10及12-01,由于两期之间下过几场大雨,所以对该边坡产生了较大的影响,为验证本文方法的有效性,在边坡稳定位置上放置用于模拟滑坡前和滑坡后的木块,木板厚度为0.05 m。

|
图 1 现场布设 Fig. 1 The scene setting |
2016-10-10对边坡进行第一次扫描,扫描的点云数据如图 2所示。对边坡进行重复扫描,并利用最邻近点搜索算法[11]提取重复扫描点云误差,如图 3所示。

|
图 2 扫描的边坡点云数据 Fig. 2 Point cloud of landslide |

|
图 3 重合度误差 Fig. 3 The overlap error |
由图 3可知,两次重复扫描的点云误差最大值为0.014 m,而圆圈中为点云空洞,其原因是在扫描的过程中,较高的土块或土石方挡住了激光射线,使得激光射线无法扫描到背面,造成空洞现象。为了验证本文提出的点云变形可靠性评价指标的准确性,在考虑测距、测角及配准误差的情况下计算边坡点云的变形可靠性评价指标,为方便及准确计算,将边坡划分为6个区域,如图 4所示。

|
图 4 对边坡进行区域划分 Fig. 4 Rigion of landslide |
利用本文方法计算得到图 4中不同区域的变形可靠性评价指标,如表 1所示。
|
|
表 1 不同区域的变形可靠性指标/m Tab. 1 The reliability indicator of deformation extraction of different regions |
由表 1可知,区域6的变形可靠性评价指标最小,而区域3的评价指标最大,为0.014 2 m,其与点云重合度误差基本相同,即说明该指标的准确性,同时也说明只有在变形大于0.014 2 m时才能被监测出来,而小于0.0142 m的变形可能被点云误差掩盖掉。
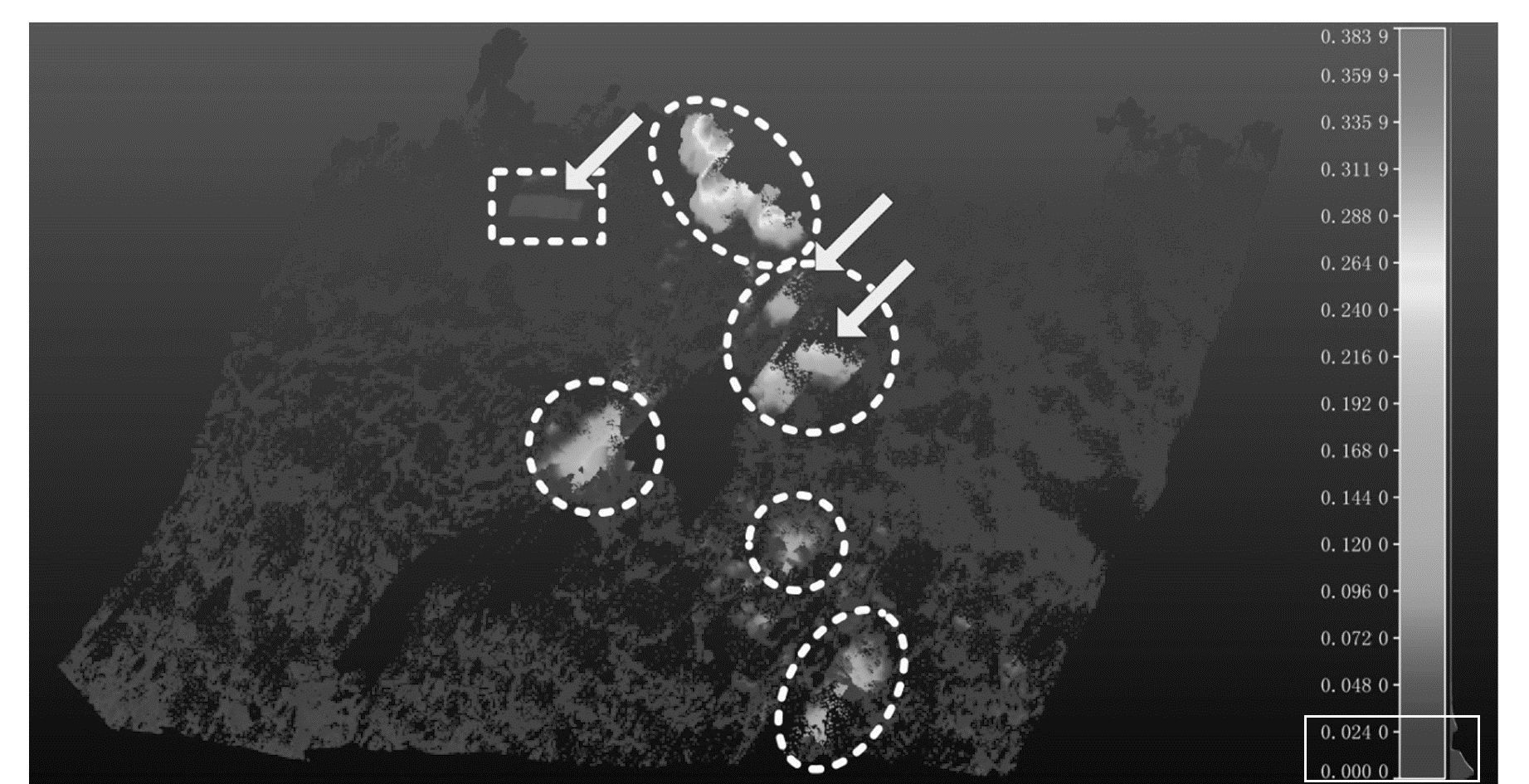
利用扫描仪在2016-12-01进行第二次扫描,并和第一次作对比分析,提取变形值,如图 5所示,并将几个大的滑坡区域进行标记。
|
图 5 变形提取结果 Fig. 5 Extraction of deformation |
由图 5可以看出,滑坡最大的地方主要集中在边坡顶部,主要原因是大雨对边坡顶部的侵蚀比较严重,而中间及右下部分也出现了几处滑坡,并标记出了滑坡方向,和图 3中圆圈标记的空洞相比,中间空洞区域大小有所减少,其原因是前方较高的土石方在雨水的冲刷下出现了滑落,从而不会挡住更多的激光射线。由图 5右边的变形标记可以看到,计算得到的最大变形量为0.383 9 m,而在图 5中出现的大部分区域分为两个主要区域的数值范围,如图中右下角矩形方框中所示,第一主要区域点云对比偏差在0.014 m以内,该偏差主要是由测距、测角、光斑及配准误差引起的,并不是真正的变形。第二主要区域点云对比偏差主要在0.035 m附近,该区域主要是模拟的滑坡区域,而模拟的实际滑坡大小为0.05 m,计算得到滑坡大小与实际滑坡大小相差0.014 m,而该值正好与点云误差引起的重合度误差相同。由图 5的颜色区分可以明显地确定滑坡区域,说明三维激光扫描具有用于区域变形监测的优点。
5 结语本文对三维激光扫描测距、测角及配准误差进行了系统分析,并利用信息熵和误差熵的关系,构建了激光点位误差熵模型。考虑相邻误差熵交集对整个点云误差熵的影响,在去除相邻误差熵交集影响的情况下,构建点云误差熵模型,并对比分析考虑相邻误差熵影响与不考虑相邻误差熵影响的点云,确定了考虑相邻误差熵影响情况下的激光点位误差熵长半轴大小,从而利用误差熵半轴长度的极值特性,实现三维激光扫描变形可靠性评价指标的确定。
利用扫描仪对某个边坡进行扫描,对第一期进行两次重复扫描,计算重复扫描点云误差,并将该误差与本文提出的变形可靠性评价指标进行对比分析,确定二者基本相同,从而验证了本文方法的有效性,同时对实际发生滑坡的边坡进行扫描,提取了滑坡区域及滑坡方向,通过对模拟滑坡和实际滑坡进行综合分析,说明变形可靠性评价指标对三维激光扫描变形监测具有指导作用。
| [1] |
徐进军, 王海城, 罗喻真, 等. 基于三维激光扫描的滑坡变形监测与数据处理[J]. 岩土力学, 2010, 31(7): 2 188-2 192 (Xu Jinjun, Wang Haicheng, Luo Yuzhen, et al. Deformation Monitoring and Data Processing of Landslide Based on 3D Laser Scanning[J]. Rock and Soil Mechanics, 2010, 31(7): 2 188-2 192)
(  0) 0) |
| [2] |
Prokop A, Panholzer H. Assessing the Capability of Terrestrial Laser Scanning for Monitoring Slow Moving Landslides[J]. Natural Hazards & Earth System Sciences, 2009, 9(6): 1 921-1 928
(  0) 0) |
| [3] |
Biasion A, Bornaz L, Rinaudo F. Laser Scanning Applications on Disaster Management[A]// Geo-Information for Disaster Management[M]. Berlin: Springer, 2005
(  0) 0) |
| [4] |
黄晓阳, 栾元重, 闫勇, 等. 基于三维激光扫描测量技术的井架变形观测[J]. 工程勘察, 2012, 4(1): 66-69 (Huang Xiaoyang, Luan Yuanzhong, Yan Yong, et al. Monitoring Deformation of Headframe Based on 3D Terrestrial Laser Scanner[J]. Geotechnical Investigation & Surveying, 2012, 4(1): 66-69)
(  0) 0) |
| [5] |
姚艳丽, 蒋胜平, 王红平. 基于地面三维激光扫描技术的滑坡模型监测与预测[J]. 测绘科学, 2014, 39(11): 42-47 (Yao Yanli, Jiang Shengping, Wang Hongping. Landslide Model Monitoring and Forecast by Using Ground 3D Laser Scanner[J]. Science of Surveying and Mapping, 2014, 39(11): 42-47)
(  0) 0) |
| [6] |
栾元重, 栾亨宣, 李伟, 等. 桥梁变形监测数据小波去噪与Kalman滤波研究[J]. 大地测量与地球动力学, 2015, 35(6): 1 041-1 046 (Luan Yuanzhong, Luan Hengxuan, Li Wei, et al. Research on Wavelet Denoising and Kalman Filter in Bridge Deformation Monitoring Data[J]. Journal of Geodesy and Geodynamics, 2015, 35(6): 1 041-1 046)
(  0) 0) |
| [7] |
Fiani M, Siani N. Comparison of Terrestrial Laser Scanners in Production of DEMs for Cetara Tower[C]. Proceedings CIPA XX International Symposium, Torino, 2005
(  0) 0) |
| [8] |
Grant D, Bethel J, Crawford M. Point-To-Plane Registration of Terrestrial Laser Scans[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2012, 72(1): 16-26
(  0) 0) |
| [9] |
Carter T. An Introduction to Information Theory and Entropy[R]. Santa Fe : Complex Systems Summer School, 2007
(  0) 0) |
| [10] |
李大军, 龚健雅, 谢刚生, 等. GIS中线元的熵不确定带研究[J]. 中国图像图形学报, 2002, 7(11): 1 214-1 220 (Li Dajun, Gong Jianya, Xie Gangsheng, et al. Research on Entropy Uncertainty Band of Linear Segments in GIS[J]. Journal of Image and Graphics, 2002, 7(11): 1 214-1 220)
(  0) 0) |
| [11] |
Abellan A, Jaboyedoff M, Oppikofer T, et al. Detection of Millimetric Deformation Using a Terrestrial Laser Scanner: Experiment and Application to a Rockfall Event[J]. Nature Hazards and Earth System Sciences, 9(1): 365-472
(  0) 0) |
2. Postdoctors Innovation and Practice Base of Wuhan Geomatics Institute, 209 Wansongyuan Road, Wuhan 430022, China;
3. Key Laboratory for Digital Land and Resources of Jiangxi Province, East China University of Technology, 418 Guanglan Road, Nanchang 330013, China;
4. School of Geodesy and Geomatics, Wuhan University, 129 Luoyu Road, Wuhan 430079, China;
5. Wuhan Optics Valley Beidou Holding Group Co Ltd, 130 Guangguqi Road, Wuhan 430206, China
 2018, Vol. 34
2018, Vol. 34

