BDS是我国自主研发的全球导航定位系统,包括5颗静止轨道卫星(GEO)、3颗倾斜同步轨道卫星(IGSO)和27颗中轨卫星(MEO)[1],GPS由24颗中轨卫星组成,两系统之间存在较大差异。陶庭叶等[2]对经验模型、高度角模型以及Helmert验后方差估计模型对BDS/GPS系统基线解算精度影响的研究表明,Helmert验后方差估计模型相对于经验模型、高度角模型有效提高了基线解算精度和可靠度;陈浩等[3]对等权模型、高度角模型、载噪比模型以及MINQUE模型对BDS/GPS系统基线解算精度影响的研究表明,4种模型的解算性能相当,高度角随机模型不适合BDS、BDS/GPS组合系统短基线解算。但以上这些成果都是针对BDS/GPS短基线解算的研究,本文主要研究常用的等权模型、高度角模型以及Helmert验后方差估计模型对BDS/GPS长基线解算精度的影响。
1 BDS/GPS长基线解算策略BDS/GPS长基线解算前必须先判断两种星座的时间基准与空间基准的一致性。时间基准分为时间系统差异和锁定信号时的接收机钟差不同步误差两部分。GPS/BDS的时间系统差异可以直接建立转换模型进行消除,但接收机锁定这两种星座时钟差并不一致[4],因此在双系统融合建立双差模型时要在不同系统内分别选取参考卫星。不同卫星系统都有自己特定的坐标基准,GPS采用WGS84坐标系统,BDS采用CGCS2000坐标系统,这两个系统坐标系的定义几乎一致,椭球参数仅有微小差异,在进行BDS/GPS长基线解算时,不需要考虑二者坐标之间的转换。
长基线解算的基本思想是:首先通过双频或三频观测值构造观测方程确定宽巷模糊度,然后结合无电离层组合观测值固定窄巷模糊度,再由已固定的宽巷和窄巷模糊度确定L1、L2载波相位的模糊度。
宽巷模糊度快速解算利用MW观测值建立如下滤波系统[5]:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{X}}_{n{\rm{ + 1}}}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{n, n + 1}}{\mathit{\boldsymbol{X}}_n} - {\mathit{\boldsymbol{W}}_{n + 1}}}\\ {E\left({{\mathit{\boldsymbol{W}}_{n + 1}}} \right) = 0, {\rm{cov}}\left({{\mathit{\boldsymbol{W}}_{n + 1}}} \right) = {\mathit{\boldsymbol{Q}}_{n{\rm{ + 1}}}}}\\ {{\mathit{\boldsymbol{L}}_{n{\rm{ + 1}}}} = {\mathit{\boldsymbol{B}}_{n{\rm{ + 1}}}}{\mathit{\boldsymbol{X}}_{n{\rm{ + 1}}}} - {\mathit{\boldsymbol{V}}_{n{\rm{ + 1}}}}}\\ {E\left({{\mathit{\boldsymbol{V}}_{n{\rm{ + 1}}}}} \right) = 0, {\rm{cov}}\left({{\mathit{\boldsymbol{V}}_{n + 1}}} \right) = {\mathit{\boldsymbol{R}}_{n{\rm{ + 1}}}}, }\\ {{\rm{cov}}\left. {\left({\mathit{\boldsymbol{V}}, \mathit{\boldsymbol{W}}} \right) = 0} \right)} \end{array}} \right. $ | (1) |
式中,
由卡尔曼滤波原理,该滤波方程的解为:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{P}}_{n, n + 1}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{n, n + 1}}{\mathit{\boldsymbol{P}}_n}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{_{n, n + 1}}^{\rm{T}} + {\mathit{\boldsymbol{Q}}_{n + 1}}\\ {\mathit{\boldsymbol{J}}_{n + 1}} = {\mathit{\boldsymbol{P}}_{n, n + 1}}\mathit{\boldsymbol{B}}_{n + 1}^{\rm{T}}{\left( {{\mathit{\boldsymbol{B}}_{n + 1}}{\mathit{\boldsymbol{P}}_{n, n + 1}}\mathit{\boldsymbol{B}}_{n + 1}^{\rm{T}}{\mathit{\boldsymbol{R}}_{n + 1}}} \right)^{-1}}\\ {\mathit{\boldsymbol{P}}_{n + 1}} = \left( {\mathit{\boldsymbol{E}}{\rm{-}}{\mathit{\boldsymbol{J}}_{\mathit{n}{\rm{ + 1}}}}{\mathit{\boldsymbol{B}}_{\mathit{n}{\rm{ + 1}}}}} \right){\mathit{\boldsymbol{P}}_{n, n + 1}}\\ {\mathit{\boldsymbol{X}}_{\mathit{n}{\rm{ + 1}}}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{n, n + 1}}{\mathit{\boldsymbol{X}}_\mathit{n}} + {\mathit{\boldsymbol{J}}_{\mathit{n}{\rm{ + 1}}}}\left( {{\mathit{\boldsymbol{L}}_{\mathit{n}{\rm{ + 1}}}}-{\mathit{\boldsymbol{B}}_{\mathit{n}{\rm{ + 1}}}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{n, n + 1}}{\mathit{\boldsymbol{X}}_\mathit{n}}} \right) \end{array} \right. $ | (2) |
式中,Pn代表权阵,其初值可由最小二乘法获得,通过式(2)可以得到宽巷模糊度和MW组合多路径效应的浮点解,通过判断ratio是否成立来固定该宽巷模糊度为NWL。
无电离层组合模糊度的快速解算原理与宽巷模糊度快速解算原理基本相同,不同的是前者在解算中使用扩波技术。其公式为:
| $ \left\{ \begin{array}{l} \hat N = \frac{{\bar N-60{N_{{\rm{WL}}}}}}{{17}}\\ {P_{\hat N\hat N}} = \frac{{{P_{\bar N\bar N}}}}{{289}} \end{array} \right. $ | (3) |
式中,N为双差电离层无关模糊度,
L1、L2模糊度固定后,将其回代到消电离层组合中,此时相位中心偏差、多路径效应、潮汐效应等误差项均已改正,对流层延迟干分量用改正模型计算,湿延迟采用窄巷模糊度固定过程中滤波得到。为了验证不同随机模型对BDS/GPS长基线解算精度的影响以及考虑CORS网络基准监测的实际需要,在消电离层组合中固定基线一端CORS基站坐标,另一端作为流动站,采用最小二乘方法解算每历元观测数据,得北东高方向解。
2 随机模型的确定双差消电离层组合观测值为:
| $ \begin{array}{l} \nabla \Delta {\varphi _{{\rm{IF}}}} = \frac{{{f_1}}}{{{f_2}}}{\left( {\varphi _2^i-\varphi _1^i-\varphi _2^i + \varphi _1^j} \right)_{\rm{L}}}_{\rm{1}}-\\ \;\;\;\;\;\;\;\;\;\;\;\;\;{\left( {\varphi _2^i - \varphi _1^i - \varphi _2^i + \varphi _1^j} \right)_{\rm{L}}}_2 \end{array} $ | (4) |
式中,
等权模型中,假设组合系统载波相位观测值精度都相同[6],设方差为σ02,构造n-1阶方差-协方差矩阵:
| $ \mathit{\boldsymbol{C = }}{\rm{2}}\sigma _0^2\left( {\frac{{f_1^2}}{{f_2^2}} + 1} \right)\left[{\begin{array}{*{20}{c}} 2&1& \cdots &1\\ 1&2& \cdots &1\\ \vdots&\vdots&\vdots&\vdots \\ 1&1& \cdots &2 \end{array}} \right] $ | (5) |
在高度角随机模型中,假设电离层延迟、对流层延迟、多路径效应、接收机噪声都与高度角有直接关系,则高度角越低,观测值精度越低。常用的高度角随机模型是正弦函数模型[7]:
| $ \sigma _i^2 = \sigma _0^2/\sin {\left( {{\rm{elev}}} \right)^2} $ | (6) |
式中,σ02为单位权方差,常设为1,elev为卫星高度角。
2.3 Helmert验后方差估计随机模型由式(1)可以得到两类相互独立的观测值
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{V}}_1} = {\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{\hat X}}{\rm{-}}\nabla \Delta \varphi _{{\rm{IF}}}^{{\rm{BDS}}}\\ {\mathit{\boldsymbol{V}}_2} = {\mathit{\boldsymbol{B}}_2}\mathit{\boldsymbol{\hat X}}{\rm{-}}\nabla \Delta \varphi _{{\rm{IF}}}^{{\rm{GPS}}} \end{array} \right. $ | (7) |
且有:
| $ \begin{array}{l} \mathit{\boldsymbol{L = }}\left[\begin{array}{l} {\mathit{\boldsymbol{L}}_{\rm{1}}}\\ {\mathit{\boldsymbol{L}}_2} \end{array} \right], \mathit{\boldsymbol{V = }}\left[\begin{array}{l} {\mathit{\boldsymbol{V}}_1}\\ {\mathit{\boldsymbol{V}}_2} \end{array} \right], \mathit{\boldsymbol{B = }}\left[\begin{array}{l} {\mathit{\boldsymbol{B}}_1}\\ {\mathit{\boldsymbol{B}}_2} \end{array} \right], \mathit{\boldsymbol{L = }}\left[{\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_1}}&0\\ 0&{{\mathit{\boldsymbol{P}}_2}} \end{array}} \right]\\ \mathit{\boldsymbol{N = }}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB = B}}_1^{\rm{T}}{\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{B}}_1} + \mathit{\boldsymbol{B}}_2^{\rm{T}}{\mathit{\boldsymbol{B}}_2}{\mathit{\boldsymbol{B}}_2} = {\mathit{\boldsymbol{N}}_{\rm{1}}} + {\mathit{\boldsymbol{N}}_2}\\ \mathit{\boldsymbol{W = }}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PL = B}}_1^{\rm{T}}{\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{L}}_1} + \mathit{\boldsymbol{B}}_2^{\rm{T}}{\mathit{\boldsymbol{B}}_2}{\mathit{\boldsymbol{L}}_2} = {\mathit{\boldsymbol{W}}_{\rm{1}}} + {\mathit{\boldsymbol{W}}_2} \end{array} $ | (8) |
残差的平方和 V1TP1V1、V2TP2V2与验后方差σ_12、σ_22的关系为:
| $ \left\{ \begin{array}{l} \left[\begin{array}{l} \sigma _{\_1}^2\\ \sigma _{\_2}^2 \end{array} \right] = {S^{-1}}\left[\begin{array}{l} \mathit{\boldsymbol{V}}_1^{\rm{T}}{\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{V}}_{\rm{1}}}\\ \mathit{\boldsymbol{V}}_2^{\rm{T}}{\mathit{\boldsymbol{P}}_2}{\mathit{\boldsymbol{V}}_2} \end{array} \right]\\ S = [{n_1}-2{\rm{tr}}\left( {{\mathit{\boldsymbol{N}}^{-1}}{\mathit{\boldsymbol{N}}_1}} \right) + {\rm{tr}}{\left( {{\mathit{\boldsymbol{N}}^{-1}}{\mathit{\boldsymbol{N}}_1}} \right)^2}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{tr}}\left( {{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{N}}_1}{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{N}}_2}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{tr}}\left( {{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{N}}_1}{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{N}}_2}} \right)\\ \;\;\;\;\;\;\;\;\;{n_2} - 2{\rm{tr}}\left( {{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{N}}_2}} \right) + {\rm{tr}}{\left( {{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{N}}_2}} \right)^2}] \end{array} \right. $ | (9) |
式中,n1为某一历元观测中有n1颗北斗卫星数据,n2为某一历元观测中有n2颗GPS卫星数据。由后验方差σ_12、σ_22再重新定权,有:
| $ {{\hat p}_i} = \frac{{\sigma _{\_1}^2}}{{\sigma _{\_i}^2P_I^{-1}}} $ | (10) |
式(9)中S的计算较为复杂,本文在实际编程中采用其简化公式计算σ_i2[8]:
| $ \sigma _{\_i}^2 = \frac{{\mathit{\boldsymbol{V}}_i^{\rm{T}}{\mathit{\boldsymbol{P}}_i}{\mathit{\boldsymbol{V}}_i}}}{{{n_i}-{\rm{tr}}\left( {{\mathit{\boldsymbol{N}}^{-1}}{\mathit{\boldsymbol{N}}_i}} \right)}} $ | (11) |
定权之后反复利用式(6)~(8)解算,直至σ_12=σ_22为止。本文中迭代终止条件是|σ_12-σ_22| < 0.001。
3 实验分析 3.1 数据介绍在四川CORS网的ZHIJ、QLAI两个测站上均使用TRM59900.00 SCIS天线和Trimble 5700双频交叉相关接收机同时接收GPS/BDS双频观测数据。数据观测时段为2016年年积日第340天,采样率为30 s,BDS/GPS组合解算时构成QLAI-ZHJI基线,长度为140 km。
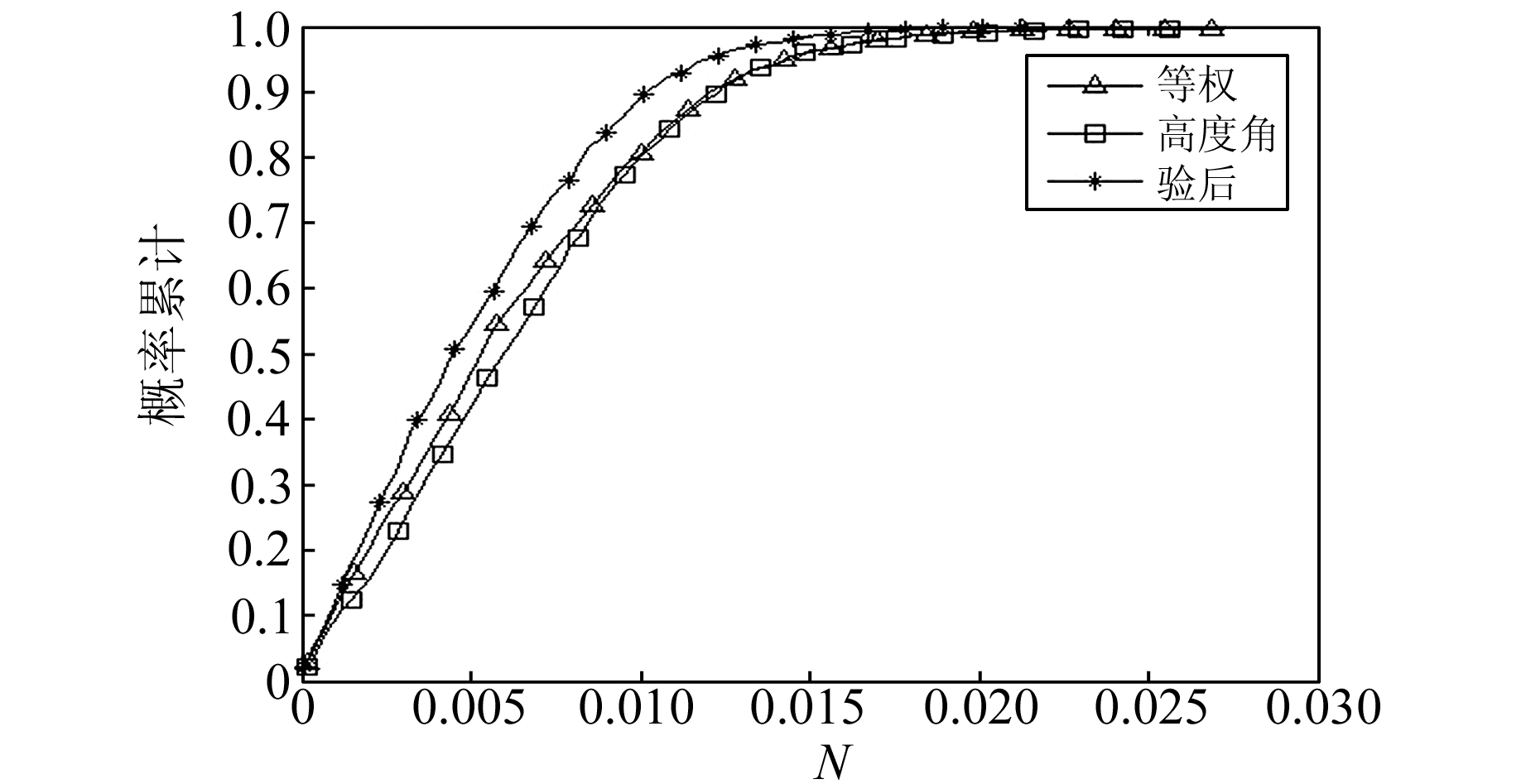
3.2 不同随机模型实验采用3种随机模型对QLAI-ZHJI基线进行长基线解算,为了分析3种随机模型对BDS/GPS组合系统解算精度的影响,分别将基线解X、Y、Z坐标偏差转换到N、E、U方向,作出U方向单历元解时间序列图, N、E方向因为3种随机模型得到的解算结果精度均在mm级,从单历元解时间序列图上较难分辨哪种随机模型精度较高,故N、E方向采用位置误差绝对值的概率分布图表示,结果如图 2~3所示。
|
图 2 N方向概率累计分布 Fig. 2 N probability cumulative distribution |
|
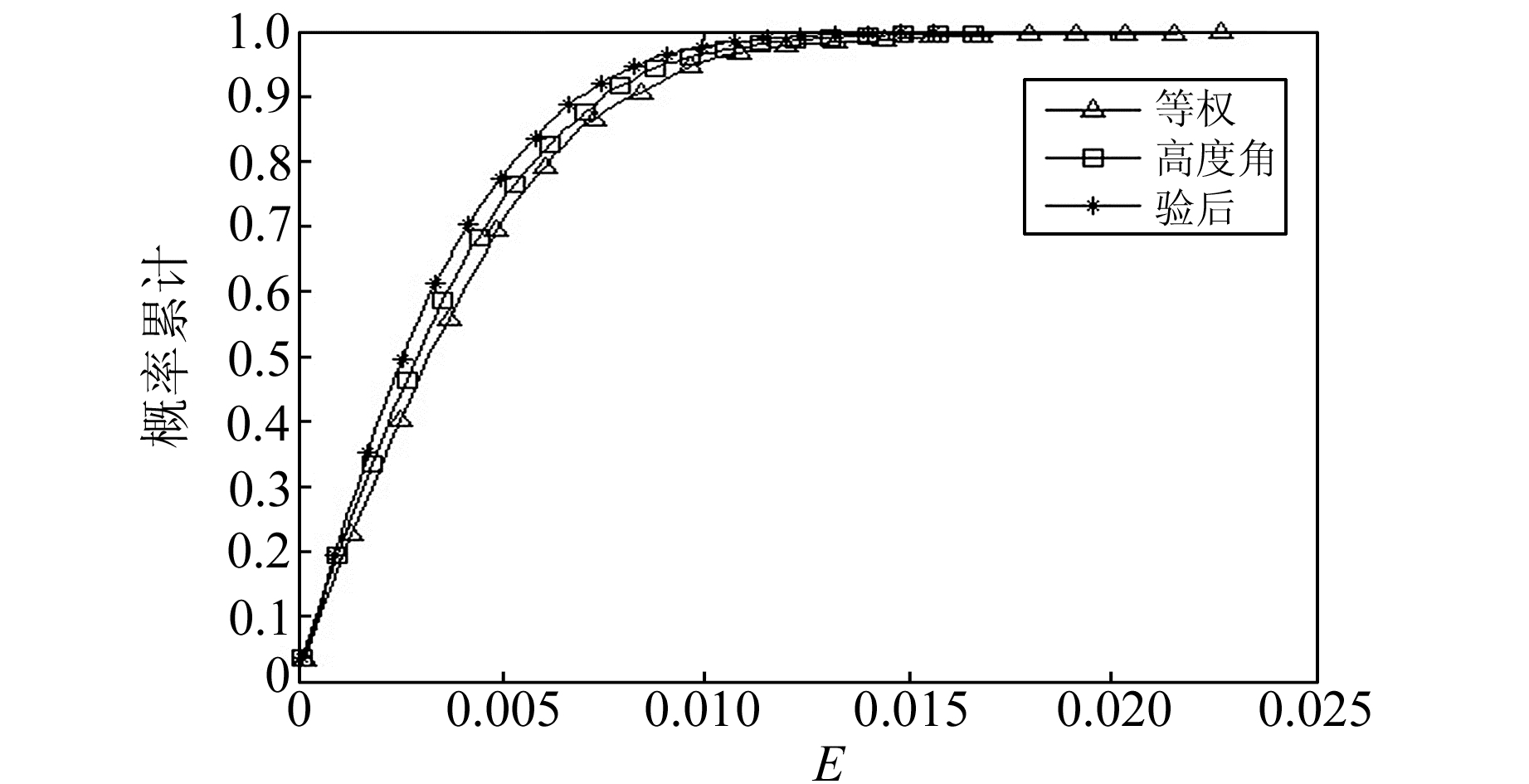
图 3 E方向概率累计分布 Fig. 3 E probability cumulative distribution |
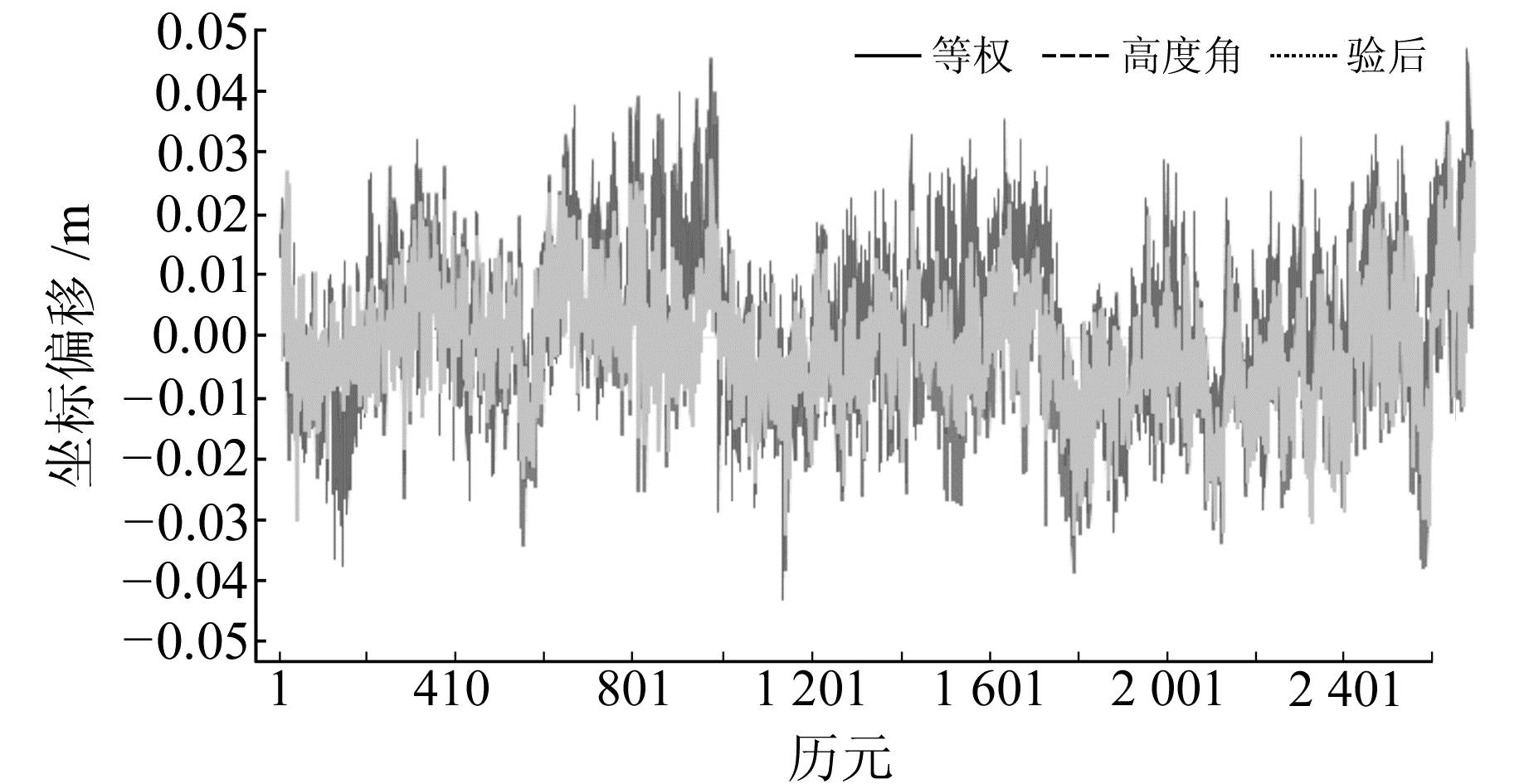
从图 1可以看出,等权随机模型与高度角随机模型在长基线U方向解的偏差基本相等;Helmert验后方差估计随机模型解的偏差明显小于等权随机模型与高度角随机模型,且波动更加平缓。从图 2~3可以看出,不管是N方向还是E方向,在位置误差概率分布图中等权随机模型与高度角随机模型的曲线非常接近,Helmert验后方差估计随机模型的曲线最陡。可知等权随机模型与高度角随机模型对BDS/GPS长基线单历元解算精度相当,Helmert验后方差估计随机模型解算精度最高。
|
图 1 3种随机模型下U方向时间序列 Fig. 1 Series diagram in three kinds of random stochastic model |
为定量统计随机模型对BDS/GPS组合系统长基线解算精度的影响,表 1给出了3种随机模型下QLAI-ZHJI基线长基线解算N、E、U方向的RMS以及标准差。
|
|
表 1 不同随机模型下长基线解算N、E、U方向的RMS以及标准差 Tab. 1 The standard deviation and RMS of long baseline N, E, U direction result in different stochastic models |
由表 1可知,不同随机模型对长基线解N、E、U方向RMS以及标准差都有不同的影响,RMS和标准差分别反映基线解算的外符合精度与内符合精度。3种随机模型中,等权模型与高度角模型解算的外符合精度与内符合精度基本相当;Helmert验后方差估计模型不管是外符合精度还是内符合精度都优于等权模型与高度角模型,水平精度提高约15%,垂向精度提高约30%。
Helmert验后方差估计模型可以提高不同精度数据组合解算精度。有理由认为,该组数据中BDS、GPS定位精度有较大差别,因此使用等权模型与高度角模型分别对BDS、GPS进行处理,验证两类数据定位精度的差别。表 2给出了2种随机模型下BDS、GPS长基线解算N、E、U方向的RMS以及标准差。从表 2可以看出,BDS、GPS两系统的RMS在等权模型与高度角模型下都存在较大差别,标准差也有差别,但相对RMS来说差别较小。对比表 1,不管采用哪种随机模型,BDS/GPS组合解算精度都优于单系统,但合理地选择随机模型可以更有效地提高组合解算的精度。
|
|
表 2 单星座系统长基线解算N、E、U方向的RMS以及标准差 Tab. 2 The standard deviation and RMS of long baseline N, E, U direction result in single constellation system |
BDS/GPS组合系统可以实现长基线高精度解算,相对于单系统增加了可同时观测到的卫星数,增强了图形结构,140 km长基线解算精度在水平向和垂向分别优于8 mm和10 mm。随机模型对长基线解算精度的影响较大,3种随机模型中,Herlmert验后方差估计模型解算精度最高;高度角随机模型和等权随机模型解算性能相当;BDS/GPS组合定位中等权模型、高度角模型定权方便,编程易实现,在精度要求不高时可以使用二者定权。
| [1] |
吴海玲, 高丽峰, 汪陶胜, 等. 北斗卫星导航系统发展与应用[J]. 导航定位学报, 2015, 3(2): 1-6 (Wu Hailing, Gao Lifeng, Wang Taosheng, et al. Development and Application of Beidou Satellite Navigation System[J]. Journal of Navigation and Location, 2015, 3(2): 1-6)
(  0) 0) |
| [2] |
陶庭叶, 王志平, 蒋俊儒. GPS/BDS单历元基线解算中随机模型的确定[J]. 大地测量与地球动力学, 2015, 35(4): 649-652 (Tao Tingye, Wang Zhiping, Jiang Junru. The Determination of Stochastic Model in GPS/BDS Single Epoch Base Settlement[J]. Journal of Geodesy and Geodynamics, 2015, 35(4): 649-652)
(  0) 0) |
| [3] |
陈浩, 许长辉, 宋现锋, 等. BDS/GPS短基线解算的随机模型研究[J]. 测绘科学, 2016, 41(3): 12-17 (Chen Hao, Xu Changhui, Song Xianfeng, et al. Study on Stochastic Model of Short Baseline Solution for BDS/GPS[J]. Scientia Geographica Sinica, 2016, 41(3): 12-17)
(  0) 0) |
| [4] |
杨旭, 范大凤, 陈小轶, 等. BDS/GPS组合基线解算软件开发及精度分析[J]. 北京测绘, 2015(2): 34-37 (Yang Xu, Fan Dafeng, Chen Xiaoyi, et al. BDS/GPS Combination of Baseline Solution Software Development and Precision Analysis[J]. Beijing Surveying and Mapping, 2015(2): 34-37)
(  0) 0) |
| [5] |
黄丁发, 周乐韬, 李成钢. GPS增强参考站网络理论[M]. 北京: 科学出版社, 2011 (Huang Dingfa, Zhou Letao, Li Chenggang. GPS Enhanced Reference Station Network Theory[M]. Beijing: Science Press, 2011)
(  0) 0) |
| [6] |
Haringer H, Brunner F K. Variances of GPS Phase Observations:The SIGMA-Mode[J]. GPS Solutions, 1999, 2(4): 35-43 DOI:10.1007/PL00012765
(  0) 0) |
| [7] |
Tiberius C, Jonkman N, Kenselaar F. The Stochastics of GPS Observables[J]. GPS World, 1999, 10(2): 49-54
(  0) 0) |
| [8] |
崔希璋, 於宗俦, 陶本藻. 广义测量平差[M]. 武汉: 武汉大学出版社, 2009 (Cui Xizhang, Yu Zongchou, Tao Benzao. Generalized Survey Adjustment[M]. Wuhan: Wuhan University Press, 2009)
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38

