2. 湖南省精密工程测量与形变灾害监测重点实验室,长沙市麓山南路932号,410083
与传统变形监测方法相比,视觉变形监测具有成本低、精度高、非接触测量的优势。随着数码相机技术的发展,普通数码相机的成像质量越来越好,为利用视觉测量技术进行精密测量提供了基础。目前,利用视觉技术进行变形监测主要有两种方式:一种是三维重建方法[1-2],该方法具有操作简便灵活、可以反映目标三维变形趋势[3-7]等优点,但是当目标纹理简单、光学路径发生弯曲时,难以提供合理、可靠的变形监测成果;另一种是针对监测目标的视觉跟踪技术,常用于二维位移监测。根据观测条件及数据处理技术的不同,又可分为室内与室外测量两类。其中室内测量由于受光照、空气湿度等的影响,如隧道、矿井等环境,因此更加注重对图像的精细化处理[8-10],但是监测距离普遍较短,无法应用在大范围、远距离的变形监测中。室外测量主要针对大坝、桥梁和建筑物等变形体。目前室外测量研究主要集中在高动态测量,例如Lee等[11-12]利用摄像机、长焦镜头等设备,对大桥振动和高层建筑的倾斜度进行实时监测都取得了较好的实验结果,但是监测距离都没有超过20 m,而且监测时间较短,忽视了长期、远距离监测时环境以及相机等设备对测量精度的影响。
随着近年来图像追踪技术的发展,目标追踪与识别的可靠性和精度得到很大改善。为此,本文以大范围、远距离的监测环境应用为目标,采用目前优秀的目标追踪与识别技术,研究基于视觉测量的二维位移监测技术与方法,包括设计具有高辨识度并适用于自动化监测的标志,考虑相机机械震动和环境等因素产生的主要误差的实时校正技术,以及基于边缘和区域识别的多目标追踪技术等。基于这些技术开发实现了数据处理系统,并通过实验验证该方法的有效性。
1 标志设计与位移测量 1.1 标志设计标志的自动识别与像元位移探测是系统实施高效率、高精度变形监测的关键之一。设标志水平移动了ΔX,定位精度是mx,位移精度是mΔx,则定位精度与位移精度的关系为:
| $ {m_{\Delta x}} = \sqrt 2 {m_x} $ | (1) |
位移精度受相机曝光时间、光电转换效率、入射辐射频率、光照度、标志边界长度等因素的影响,根据式(1),可以将位移误差公式表示为[13]:
| $ {m_{\Delta x}} = \frac{{\sqrt 2 }}{{M \cdot \Delta E(l + \Delta x \cdot {\rm{ctg}}\theta )}}{m_Q} $ | (2) |
式中,mQ为相机光感应误差;当相机确定时,曝光时间、光电转换效率、入射辐射频率都为常数,统一将其表示为M;ΔE=Evz-Evb,Evz为标志面光照度,Evb为标志背景光照度,则ΔE为标志光照度反差;l表示标志分界线在横向和纵向的投影长度;Δx·ctgθ为常数。由式(2)可知,位移探测误差受标志光照度反差的影响,反差越大,精度越高;位移探测误差还受到标志边界投影长度的影响,长度越长,精度越高。
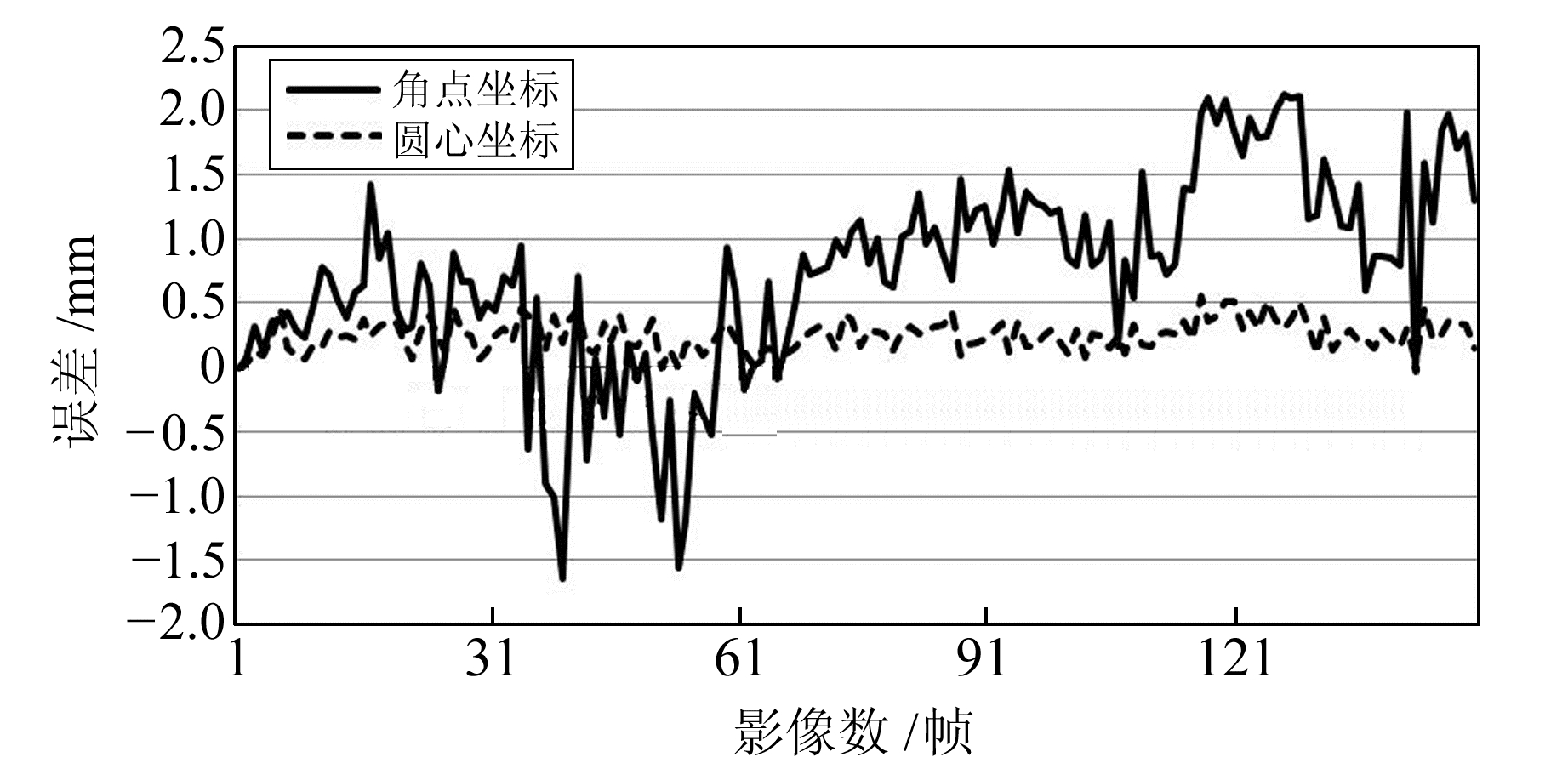
本文实验使用黑白相机。黑白相机获取的影像具有更好的锐度,适合进行高精度测量。结合该特点,将标志颜色设为反差较为明显的黑色与白色并尽可能增加标志边界投影长度。考虑到角点与圆心提取方式,将方形或圆形作为标志图像特征,分别设计标志。在测量距离为60 m时进行静态测量实验,共拍摄150组照片,使用相机型号为佳能600D,有效像素1 800万,镜头焦距135 mm。测量误差曲线如图 1所示。
|
图 1 坐标提取误差对比 Fig. 1 Comparison between coordinate extracting errors |
从图 1测量结果中可以看出,在拍摄距离远、标志边缘模糊的情况下,圆形标志由于其特殊的几何形状,可以很好地限制误差范围,而角点坐标提取受边缘模糊的影响较大,精度比圆形标志低。因此,最终选择圆形作为标志图像特征。
1.2 基于标志形状匹配的多目标追踪选取合适的ROI(region of interest)是标志坐标能否正确提取的前提。由于变形监测应用中相机至监测目标的距离一般较远,标志在影像中的成像范围比较小。如果每次坐标提取时都对整幅影像进行处理,将耗费更多的时间,并增加坐标提取的难度。因此,有必要在坐标提取之前选取合适的标志区域,提高坐标提取的效率与精度。
采用基于图像灰度相关的ROI计算方式在远距离测量中容易受到遮挡、光照不均匀、噪声等因素的影响,导致数据处理计算量大、匹配正确率低。针对这种情况,本文在基于形状的目标匹配方法中,加入KCF(kernelized correlation filter)[14]目标追踪,形成多目标匹配与追踪方法。该方法能够快速识别并追踪目标,尤其是在监测距离远、目标范围小、光照变化明显的情况下,具有很好的追踪精度。利用该方法,可以将ROI限定在一个很小的范围内,从而大大缩短数据处理时间。
1.3 标志坐标精确提取本文使用最小二乘曲线拟合方法寻找标志圆心坐标。对于圆特征来说,常见的曲线形式有圆和椭圆,而在实际测量中,拍摄到的标志影像的圆特征更加接近椭圆形。因此,利用椭圆公式逼近圆特征,鲁棒性和精度会更高。为提高圆心坐标的提取精度,还需要对影像进行适当处理,具体步骤如下:1)将目标匹配得到的ROI提取出来;2)对ROI进行双边滤波处理;3)边缘检测;4)有效边缘筛选。在提取到的图像边缘中,不仅包含椭圆边缘,同时还包含一些多余边缘,因此需要对边缘进一步处理,准确地提取椭圆边缘[15]。考虑到椭圆边缘特征,首先剔除非闭合环,如果边缘点集合的首尾像素点的距离超过1.5个像素,则认为不是闭合环并予以剔除。但这样仍无法剔除一些闭合但不是椭圆的边缘。为此,结合圆形特征,先利用式(3)计算圆形形状因子:
| $ \left\{ \begin{array}{l} C'' = \frac{F}{{({\rm{ma}}{{\rm{x}}^2} \times {\rm{ \mathsf{ π} }})}}\\ C = {\rm{min}}\left( {1, C''} \right) \end{array} \right. $ | (3) |
式中,F为闭合区域的面积;max为闭合区域中心点距离边缘点的最大值;C为形状因子,C的值越接近1,闭合区域的形状越接近圆形。通过设置合适的阈值,最终选择出目标椭圆。
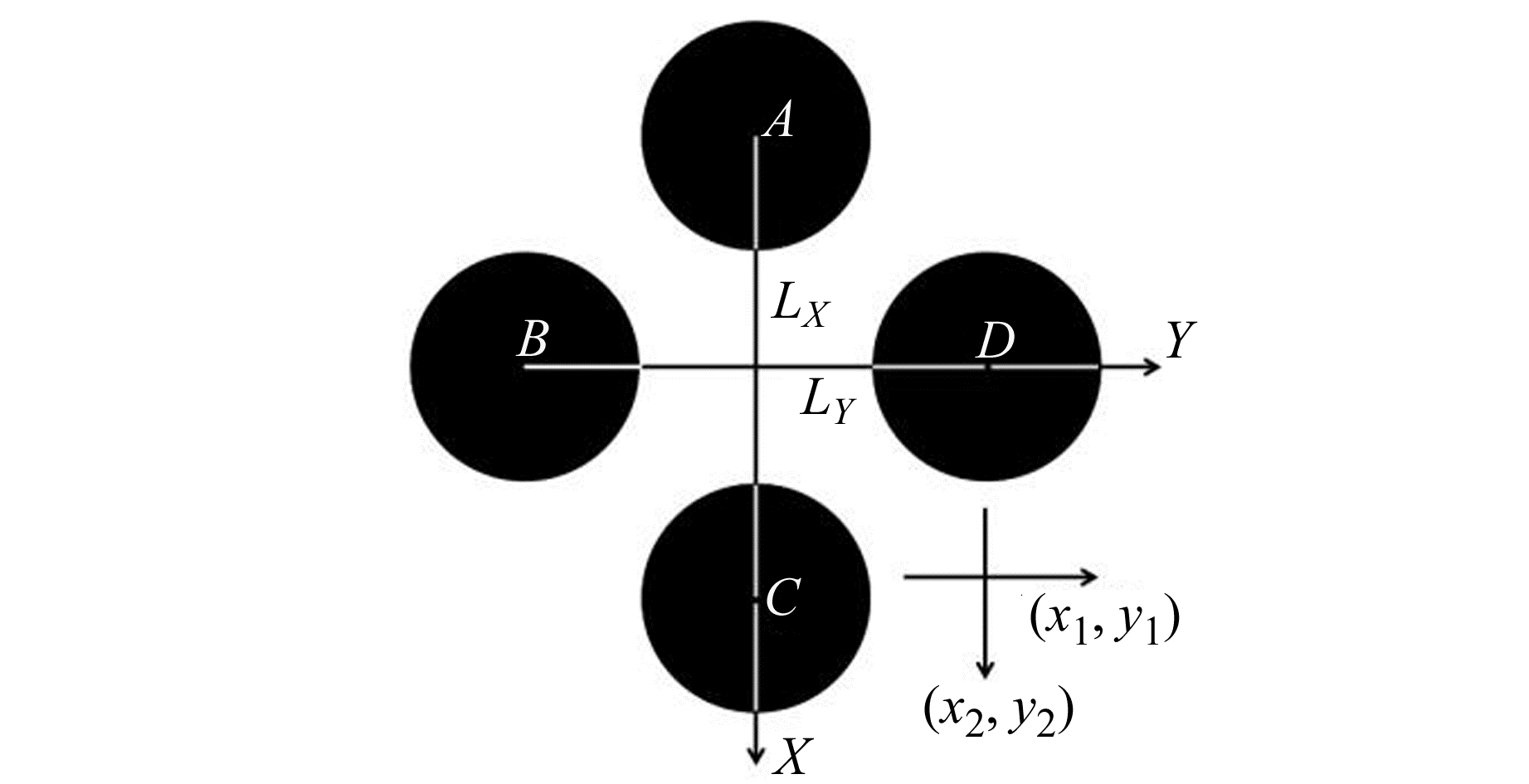
1.4 位移计算在实际监测中,相机对标志可能不是正直摄影,因此空间目标到像平面的投影将不可避免地发生畸变,使图像上标志的位移与实际位移产生偏差,从而无法正确反映真实位移。针对该问题,对计算得到的位移进行校正处理。如图 2所示,已知LX和LY分别为标志水平和竖直方向的圆心距离,单位为mm。以图像左上角为坐标原点绘制坐标系,将提取的4个圆心分别记为A、B、C、D,坐标单位为像素。
|
图 2 标志实际位移换算 Fig. 2 Actual displacement calculation of mark |
处理流程为:每提取一次圆心时,就将4个圆心坐标与初始坐标求差,得到水平方向位移量mx与垂直方向位移量my;计算BD方向向量x =[x1 y1]T和AC方向向量y =[x2 y2]T;计算BD和AC方向圆心距离在图像上的长度,记为Sx和Sy,单位为像素;计算比例系数SFX=LX/Sx,SFY=LY/Sy。利用式(4)计算标志变换矩阵:
| $ \mathit{\boldsymbol{T}} = {\left[{\begin{array}{*{20}{c}} {{X_1}}&{{X_2}}\\ {{Y_1}}&{{Y_2}} \end{array}} \right]^{ -1}} $ | (4) |
式中,
| $ \begin{array}{*{20}{c}} {\left[{\begin{array}{*{20}{c}} {{\rm{d}}x}&{{\rm{d}}y} \end{array}} \right]{^{\rm{T}}} = }\\ {{{\left[{\begin{array}{*{20}{c}} {{\rm{S}}{{\rm{F}}_X}}&0\\ 0&{{\rm{S}}{{\rm{F}}_Y}} \end{array}} \right]}^{\rm{T}}}{{\left[{\begin{array}{*{20}{c}} {{m_x}}&{{m_y}} \end{array}} \right]}^{\rm{T}}}} \end{array} $ | (5) |
光线在空气中传播时受到大气温度、气压、密度、湿度等客观条件的影响,传播路径会发生变化,导致标志发生位移,或形状发生变化,进而导致位移计算出现误差、坐标提取不正确。由于气象条件改变引起的误差具有随机性,目前还没有一个有效的误差改正模型。针对缓慢变形监测的实际情况,可以认为变形体在较短时间内是静止不动的,因此采用连续拍摄取平均的方式削弱一部分随机误差。
2.2 单反相机震动对精度的影响及改正相机在长时间拍照过程中,姿态并不能保证绝对不变,单反相机会受到相机反光板和快门机械震动的影响。当监测距离较远时,即便是轻微的震动,也会产生较大的测量误差。通过实验发现,当监测距离为90 m时,相机姿态改变引起的误差在2~5 mm;当监测距离为100 m时,引起的误差超过5~10 mm,因此有必要对其加以改正。
图像对齐是一种基于像素灰度值的匹配技术,可以从具有一定程度重叠的两幅图像中发现对应关系,被广泛地应用于视频稳定和影像拼接中[16]。相机机械震动是一种高频震动,在每两次拍摄间歇都会产生一个瞬时位移,主要表现为像平面的整体移动,因此,影像的仿射变换与相似性变换引起的误差可以忽略不计,主要考虑二维偏移引起的误差。
利用图像对齐技术对相机姿态偏移改正的前提是相机视场范围内有静止不动的区域,通过对该区域进行亚像元灰度匹配,可以找到任意两幅影像之间的偏差。当相机采取连拍模式时,每两次拍摄间隔的时间非常短,因此可以认为在每两次拍摄间隔内目标没有发生位移。由于该区域被认为是静止不动的,则计算得到的偏差即为相机姿态偏移引起的测量误差。
通过模拟实验,对相机姿态校正效果及测量精度进行检验。分别在相距90 m的两台脚架上安置单反相机与可移动式基座,基座上固定标志,设定相机每隔5 min拍摄一次,在每次拍摄间隔基座水平移动20 mm。
对获取的影像序列进行两次处理:第一次不改正;第二次利用图像对齐技术进行改正,选取影像中某一块稳定不变的矩形区域作为静态匹配区域。实验结果及误差如图 3所示。

|
图 3 模拟实验结果 Fig. 3 Simulation results |
分析实验结果可以发现,即便对相机机身与镜头都进行了加固,但是由于快门及反光板的震动,最大测量误差仍然达到了3 mm,而经过校正后,测量误差控制在1 mm以内。
3 系统设计与实验 3.1 系统组成与软件设计本文设计的位移监测系统主要由标志、单反相机(配备长焦镜头)、笔记本电脑以及数据处理软件组成,基于VS2015/QT平台与C++编程语言,利用相机自带的软件开发包开发数据处理软件,从相机实时接收数据并计算结果。
3.2 位移监测实验本次实验使用佳能600D相机,设置拍摄影像大小为5 184×3 456,有效像素1 800万,镜头焦距135 mm。实验场地选为两栋大楼,在其中一栋大楼楼顶放置三脚架,三脚架上安放定制的单反相机底座,并将相机固定在底座上;在另一栋大楼楼顶距离相机75 m的墙面上粘贴纸质标志,用于静态测量实验;在距离相机100 m的位置摆放脚架,安置可移动式基座与标志,用于模拟变形监测实验。
首先进行为期3 d(2016-06-20~06-22)的静态测量实验,监测时间为9:00~17:00,相机拍摄间隔为6 min,每次连续拍摄8张影像,利用位移监测软件对数据进行处理。由于雾霾、阴雨等不利气象条件会使标志的识别率降低,得到的有效结果会少于影像数目。位移变化趋势如图 4所示。

|
图 4 静态测量实验结果 Fig. 4 Static measurement results |
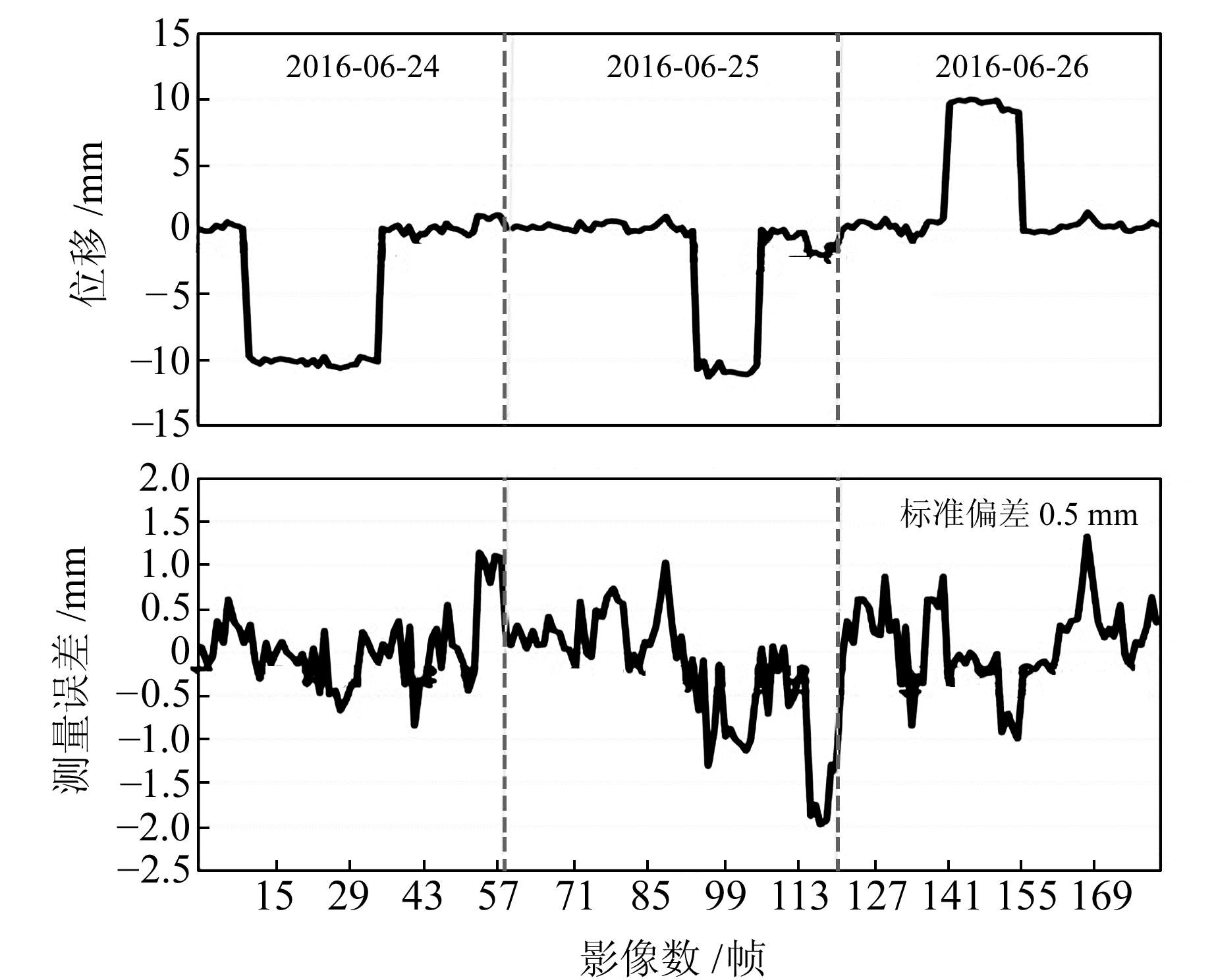
进一步进行模拟变形测量的实验,监测期为2016-06-24~06-26,监测时间为9:00~17:00。设置相机拍摄间隔为8 min,每次连续拍摄8张影像。在拍摄过程中,调整可移动式基座,使标志水平移动10 mm,每天来回移动两次,位移趋势与测量误差统计如图 5所示。
|
图 5 模拟变形测量实验结果 Fig. 5 Simulated deformation measurement results |
当监测距离为100 m时,该方法能够准确地反映目标的变化,最大误差控制在2 mm以内。
继续开展实验,对相机及软件在远距离、长期监测中的稳定性、精度进行评估。将单反相机安置在室外水泥观测墩上,加装防水罩,在距离相机320 m处的大楼一楼位置粘贴监测标志,由于大楼一楼足够稳定,因此可以认为监测目标是静止不动的。使用佳能600D及150 mm定焦镜头,通过数据线与电脑连接,拍摄到的目标影像如图 6所示。

|
图 6 目标影像 Fig. 6 The target image |
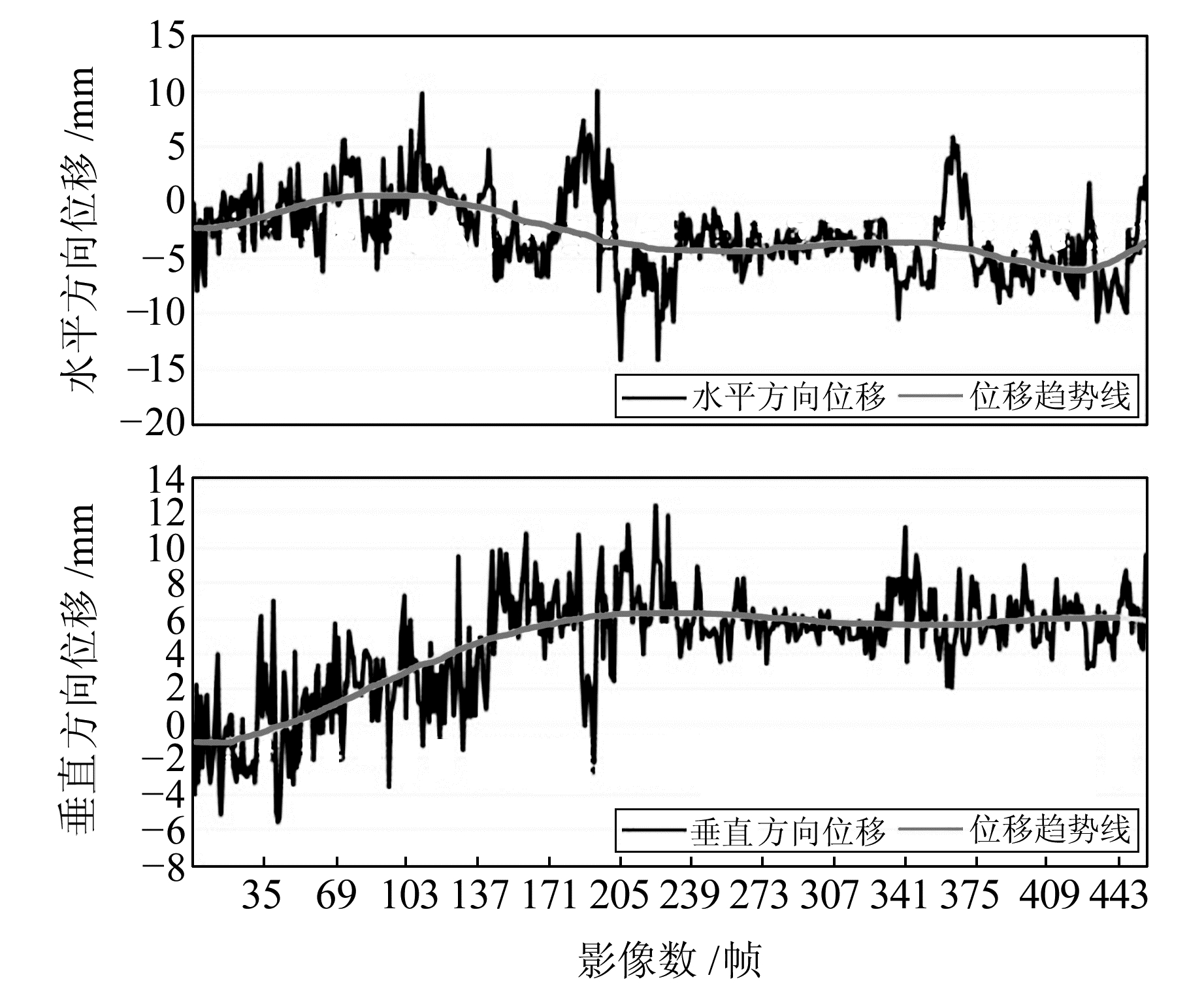
连续进行7 d的监测,利用软件对数据进行实时处理,监测结果如图 7所示。
|
图 7 长期观测实验结果 Fig. 7 Experimental results of long-term observation |
当监测距离拉大到320 m时,监测精度下降较为明显。剔除部分粗差后,水平方向标准偏差为3.5 mm,垂直方向标准偏差为4.8 mm。下面对主要误差源进行分析。
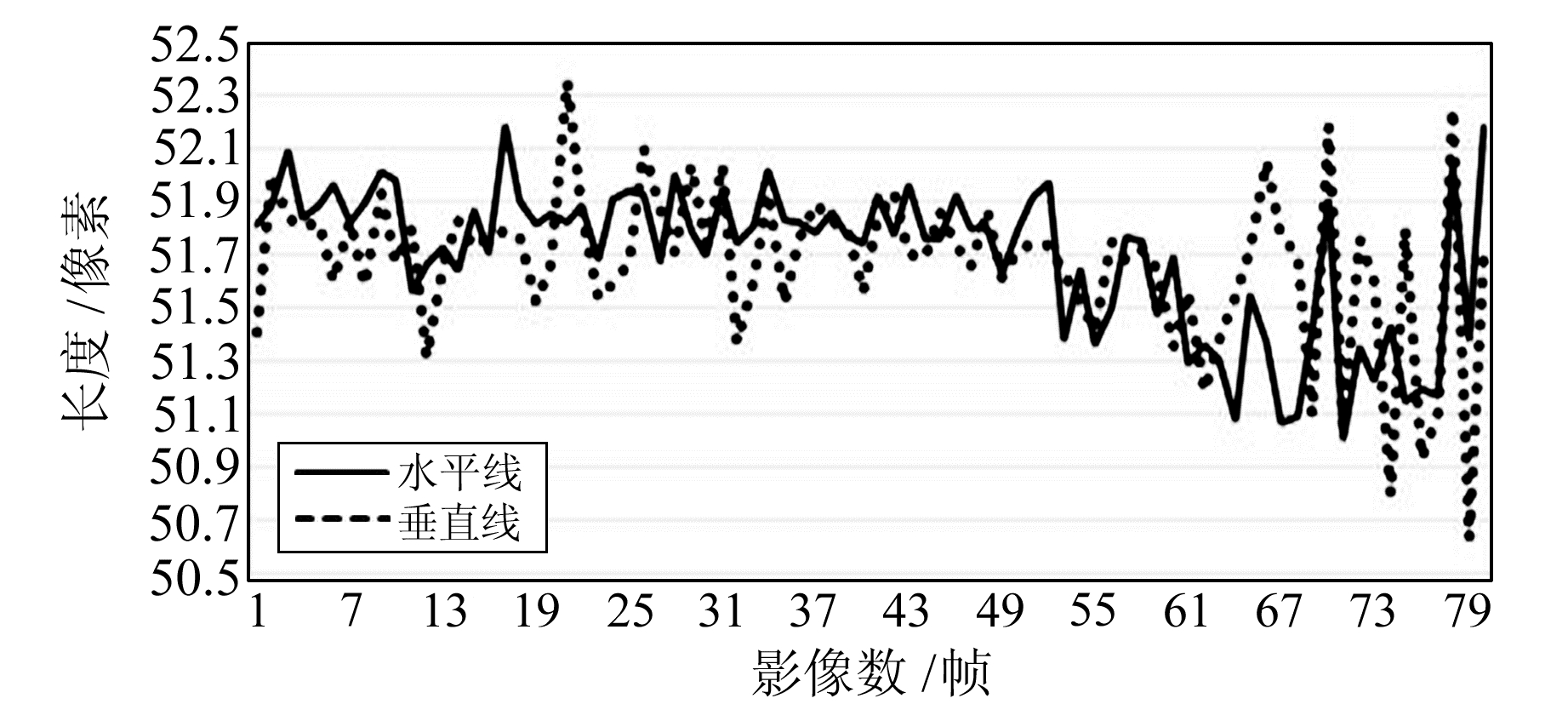
1) 相机分辨率与大气湍流。标志4个圆心之间的距离保持不变,假如坐标提取完全正确,则圆心水平线长度与垂直线长度应该保持不变。提取其中1 d的数据,计算水平线与垂直线长度(图 8)。可以发现,前后两次长度差值最大可以达到2.6像素,而本次实验中单个像素对应的实际尺寸为4.65 mm,那么由此引起的观测偏差最大可达12.1 mm。除了由于大气湍流导致的标志形状微变,最主要的因素在于相机分辨率不足,当监测距离较远时,单个像素对应的实际尺寸过大,坐标提取精度会大幅下降。
|
图 8 水平线与垂直线长度统计 Fig. 8 Statistics of length of horizontal and vertical lines |
2) 镜身形变。虽然水平方向的波动幅度较大,但通过绘制变形趋势线发现,水平方向变形趋势稳定,与实际情况相符;而垂直方向变形趋势逐渐上扬。分析其主要原因在于:镜头组成结构较为复杂,内部元器件受温度影响较大,长时间放置在室外,镜身会因为热胀冷缩发生形变,导致光轴及视野区域发生偏移;又因为镜头本身较重,使偏移在垂直方向发生不可逆的变化。
除此之外,雾霾、阴雨等气象因素都会对坐标的提取产生一定的影响。
4 结语本文通过一系列实验,验证了基于视觉测量的变形监测方法的可行性和有效性以及监测精度。目前来看,本方法仍然存在一些不足:1)标志识别精度不够高,受气象因素、遮挡的影响较大,错误识别率仍然较高;2)相机自身的稳定性也是影响测量精度的主要因素,如何固定相机、如何保持相机的工作温度,是在实际应用中必须要考虑的问题;3)由于受到相机分辨率以及目标识别算法的限制,监测距离与监测精度仍然有限。但是,随着计算机视觉理论算法和图像传感器的发展,视觉变形监测系统也将会朝着精度更高、成本更低、距离更远的方向发展。
| [1] |
Moulon P, Monasse P, Marlet R. Adaptive Structure from Motion witha Contrario Model Estimation[A]//Computer Vision-ACCV 2012[M]. Springer Berlin Heidelberg, 2012
(  0) 0) |
| [2] |
Moulon P, Monasse P, Marlet R. Global Fusion of Relative Motions for Robust, Accurate and Scalable Structure from Motion[C]. IEEE International Conference on Computer Vision, 2013 http://www.researchgate.net/publication/261622957_Global_Fusion_of_Relative_Motions_for_Robust_Accurate_and_Scalable_Structure_from_Motion
(  0) 0) |
| [3] |
Galantucci L M, Pesce M, Lavecchia F. A Powerful Scanning Methodology for 3D Measurements of Small Parts with Complex Surfaces and Sub Millimeter-Sized Features, Based on Close Range Photo Grammetry[J]. Precision Engineering, 2016, 43: 211-219 DOI:10.1016/j.precisioneng.2015.07.010
(  0) 0) |
| [4] |
Park S W, Park H S, Kim J H, et al. 3D Displacement Measurement Model for Health Monitoring of Structures Using a Motion Capture System[J]. Measurement, 2015, 59: 352-362 DOI:10.1016/j.measurement.2014.09.063
(  0) 0) |
| [5] |
Elharrouss O, Moujahid D, Tairi H. Motion Detection Based on the Combining of the Background Subtraction and the Structure-Texture Decomposition[J]. Optik-International Journal for Light and Electron Optics, 2015, 126(24): 5 992-5 997 DOI:10.1016/j.ijleo.2015.08.084
(  0) 0) |
| [6] |
姜平安. 基于视频图像的结构振动监测研究[D]. 杭州: 浙江大学, 2011 (Jiang Ping'an. Video Grammetric Technique-Based Monitoring of Structural Vibration[D]. Hangzhou: Zhejiang University, 2011) http://cdmd.cnki.com.cn/Article/CDMD-10335-1011204122.htm
(  0) 0) |
| [7] |
武金浩. 基于视觉计算的煤矿巷道形变监测方法的研究[D]. 西安: 西安科技大学, 2013 (Wu Jinhao. Research on the Method for Deformation Monitoring of Coal Mine Roadway Based on Visual Computing[D]. Xi'an: Xi'an University of Science and Technology, 2013) http://cdmd.cnki.com.cn/Article/CDMD-10704-1014000307.htm
(  0) 0) |
| [8] |
赵炯, 朱海涛, 屈剑平, 等. 基于OpenCV的圆心定位在地铁隧道变形监测中的应用[J]. 传感器与微系统, 2013(11): 139-142 (Zhao Jiong, Zhu Haitao, Qu Jianping, et al. Application of Canter of Circle Location in Metro Tunnels Deformation Monitoring Based on OPENCV[J]. Sensors and Microsystems, 2013(11): 139-142 DOI:10.3969/j.issn.1000-9787.2013.11.041)
(  0) 0) |
| [9] |
王宪. 强干扰条件下精密视觉测量技术及应用研究[D]. 长沙: 中南大学, 2013 (Wang Xian. Research on Precision Vision Measurement Technology and Its Applications under Strong Interference Conditions[D]. Changsha: Central South University, 2013) http://cdmd.cnki.com.cn/Article/CDMD-10533-1014404208.htm
(  0) 0) |
| [10] |
孙久运. 矿区变形监测精密近景摄影测量关键技术研究[D]. 徐州: 中国矿业大学, 2010 (Sun Jiuyun. Research on Key Technology of Precision Close-range Photo Grammetry for Deformation Monitoring in Mining Area[D]. Xuzhou: China University of Mining and Technology, 2010) http://cdmd.cnki.com.cn/Article/CDMD-10290-2010280104.htm
(  0) 0) |
| [11] |
Lee J J, Shinozuka M. A Vision-Based System for Remote Sensing of Bridge Displacement[J]. Ndt & E International, 2006, 39(5): 425-431
(  0) 0) |
| [12] |
Lee J H, Ho H N, Shinozuka M, et al. An Advanced Vision-Based System for Real-Time Displacement Measurement of High-Rise Buildings[J]. Smart Materials and Structures, 2012, 21(12): 125 019 DOI:10.1088/0964-1726/21/12/125019
(  0) 0) |
| [13] |
易学锋. 单反数码相机精密位移测量研究[D]. 武汉: 武汉大学, 2009 (Yi Xuefeng. Research on Precision Displacement Measurement with Digital Single Lens Reflex Camera[D]. Wuhan : Wuhan University, 2009) http://cdmd.cnki.com.cn/Article/CDMD-10486-1011071203.htm
(  0) 0) |
| [14] |
Henriques J F, Caseiro R, Martins P, et al. High-Speed Tracking with Kernelized Correlation Filters[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(3): 583-596 DOI:10.1109/TPAMI.2014.2345390
(  0) 0) |
| [15] |
Perona P, Malik J. Scale-Space and Edge Detection Using Anisotropic Diffusion[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990, 12(7): 629-639 DOI:10.1109/34.56205
(  0) 0) |
| [16] |
Szeliski R. Image Alignment and Stitching: A Tutorial[J]. Foundations and Trends in Computer Graphics and Vision, 2004, 2(11-12): 273-292
(  0) 0) |
2. Key Laboratory of Precise Engineering Surveying & Deformation Disaster Monitoring of Hunan Province, 932 South-Lushan Road, Changsha 410083, China
 2018, Vol. 38
2018, Vol. 38


