2. 湖南省有色地质勘查局二四七队,长沙市东六路100号,410129
我国现行的参心坐标系统主要包括1954北京坐标系和1980西安坐标系,地心坐标系统以2000国家大地坐标系(CGCS2000)为主。为了成果的转换和统一,坐标系统之间常常要进行各种转换,主要分为同一坐标系统之间不同形式的转换和不同坐标系统之间的转换[1-2]。
我国的基础设施建设并不是在空间坐标系或椭球面上开展的,需要将椭球面或空间直角坐标投影到高斯平面或施工面上。为了克服投影变形,需要采用分带投影,造成同一区域处在不同的坐标系统中,涉及到不同坐标系之间的转换。对于平面坐标系统转换问题,通常选择在两个不同坐标系中公共点的两套坐标,利用坐标转换公式解算出转换参数,但我国大部分地区高斯平面直角坐标值x、y都比较大,构造的法方程矩阵容易出现病态,导致求解的转换参数不可靠。刘陶胜等[3]提出通过附加重心基准条件解决转换矩阵严重病态的问题,但该方法仅在理论上进行分析,未给出具体的计算方法。正则化方法可解决法方程的病态问题[4-5],但方法本身并不完善,存在不稳定性。本文对系数矩阵的病态性问题进行分析,提出将基准旋转中心引入区域坐标转换中来解决该问题。
1 病态方程组产生的原因及判断标准对于n维向量x、y,当‖x‖≠0、‖y‖≠0时,x与y的夹角
设方程组Ax = b的系数矩阵A是一个n×n的矩阵,其中aj=(a1j, a2j, …, anj)T,j=1, 2, …, n。对于A,必然存在一组实数k1,k2,…, kn,使得k1a1+k2a2+…+kn-1an-1≈b为an的最佳逼近,定义向量组的相关程度r(a1, a2, …, an)=r(an, b),则:
1) 当b = an时,r(a1, a2, …, an)=1,即线性相关,A的行列式D=0;
2) 当b → an时,此时,D=0,r(a1, a2, …, an)→1;
3) 当b ⊥ an时,即向量组a1, a2, …, an两两垂直,r(a1, a2, …, an)=0,D是一个相对较大的值。
根据Cramer法则,当D≠0时,方程组解有唯一解:
| $ {x_i} = \frac{{{D_i} + \mathit{\Delta }{D_i}}}{{D + \mathit{\Delta }D}} = \frac{{{D_i}}}{{D + \mathit{\Delta }D}} + \frac{{\mathit{\Delta }{D_i}}}{{D + \mathit{\Delta }D}} \approx \frac{{{D_i}}}{D} $ | (1) |
当向量组a1, a2, …, an相关程度较小时,较小的扰动对方程的结果影响不大;但当相关程度较大时,D较小,扰动对结果的影响将随相关程度的增加而迅速变化。
引入A的条件数cond来判读方程组的性态,当cond相对大时,称为病态方程组,反之为良态。解和cond的关系为:
| $ \frac{{\left\| {\delta \mathit{\boldsymbol{x}}} \right\|}}{{\left\| \mathit{\boldsymbol{x}} \right\|}} \le {\rm{cond}}\left( \mathit{\boldsymbol{A}} \right)\left( {\frac{{\left\| {\delta \mathit{\boldsymbol{b}}} \right\|}}{{\left\| \mathit{\boldsymbol{b}} \right\|}} + \frac{{\left\| {\delta \mathit{\boldsymbol{A}}} \right\|}}{{\left\| \mathit{\boldsymbol{A}} \right\|}}} \right) $ | (2) |
式中,δA和δb为A和b的扰动量,δx为扰动所引起的解的误差。
矩阵病态性主要分为:行列式很大或很小;元素间相差大数量级,且无规则;主元消去过程中出现小主元;特征值相差大数量级。
2 系数矩阵的病态性分析设原坐标系中坐标向量为(x1, y1),对应新坐标系中为(x2, y2),原、新坐标系之间的平移参数为(Δx, Δy),两轴之间的夹角为α,比例参数为k,则两套坐标的转换关系为:
| $ \left[ {\begin{array}{*{20}{c}} {{x_2}}\\ {{y_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\Delta x}\\ {\Delta y} \end{array}} \right] + k\left[ {\begin{array}{*{20}{c}} {\cos \alpha }&{\sin \alpha }\\ { - \sin \alpha }&{\cos \alpha } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_1}}\\ {{y_1}} \end{array}} \right] $ | (3) |
令p=kcosα,q=ksinα,得:
| $ \left[ {\begin{array}{*{20}{c}} {{x_2}}\\ {{y_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\Delta x}\\ {\Delta y} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} p&q\\ { - q}&p \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_1}}\\ {{y_1}} \end{array}} \right] $ | (4) |
式(4)的矩阵形式为:
| $ \left[ {\begin{array}{*{20}{c}} {{x_2}}\\ {{y_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0&{{x_1}}&{{y_1}}\\ 0&1&{{y_1}}&{ - {x_1}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta x}\\ {\Delta y}\\ p\\ q \end{array}} \right] $ | (5) |
式(5)表示为:
| $ \mathit{\boldsymbol{Bx}} = \mathit{\boldsymbol{L}} $ | (6) |
式中,
| $ \mathit{\boldsymbol{x}} = {\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B}}} \right)^{ - 1}}\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{L}}} \right) = {\mathit{\boldsymbol{N}}^{ - 1}}\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{L}}} \right) $ | (7) |
假设有g个公共点,则法方程矩阵N为:
| $ \mathit{\boldsymbol{N}} = \\ \left[ {\begin{array}{*{20}{c}} g&0&{{x_1} + \cdots + {x_g}}&{{y_1} + \cdots + {y_g}}\\ 0&g&{{y_1} + \cdots + {y_g}}&{ - {x_1} - \cdots - {x_g}}\\ {{x_1} + \cdots + {x_g}}&{{y_1} + \cdots + {y_g}}&{x_1^2 + \cdots + x_g^2 + y_1^2 + \cdots + y_g^2}&0\\ {{y_1} + \cdots + {y_g}}&{{x_1} + \cdots + {x_g}}&0&{x_1^2 + \cdots + x_g^2 + y_1^2 + \cdots + y_g^2} \end{array}} \right] $ | (8) |
式中,法方程N为4阶满秩正定矩阵,其解是唯一的。
由于我国高斯平面直角坐标值(x, y)都比较大,以m为单位有6~7位整数(上千km),使式(9)中N的元素相差很大,且无规则。对坐标转换中公共点的坐标进行较小的扰动时,则N呈现高度病态,根据式(7)得出的结果波动很大,求解的转换参数不可靠。
利用§4中前4个公共点的1980西安坐标系和CGCS2000平面坐标进行转换参数计算,法方程N的条件数cond(N)=8.237×1016,为严重病态。若对1个公共点在1980西安坐标系中的x增加1 cm和2 cm扰动,平移参数的变化达到20.3 cm,见表 1。由表可知,系数矩阵B增加较小的波动,平移参数的变化非常显著。
|
|
表 1 病态矩阵对参数的扰动影响 Tab. 1 Fluctuating effect of ill-matrix on parameters |
式(3)中的坐标转换是围绕中央子午线与赤道面的交点(坐标原点)进行的,即隐含了坐标原点:
| $ \left[ {\begin{array}{*{20}{c}} {{x_2} - 0}\\ {{y_2} - 0} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\Delta x}\\ {\Delta y} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} p&q\\ { - q}&p \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_1} - 0}\\ {{y_1} - 0} \end{array}} \right] $ | (9) |
如图 1所示,由于转换区域1(公共点集)距坐标转换的基准中心O2有上千km,构成的系数矩阵中元素相差好几个数量级,转换区域1中的转换点出现微小变化时会产生细微的角度变化,再加上转换区域1距基准中心O1的距离很大,两者共同作用会引起平移参数的显著变化。为减小转换区域与基准中心之间的距离,分别将基准中心移到转换区域中,使基准中心与转换点之间的距离大为减小,也使得转换区域离坐标转换的基准中心O2的距离大为缩短。如图 2所示,原坐标系x1O1y1和x2O2y2的基准中心O1和O2移到新坐标x′1O′1y′1和x′2O′2y′2的基准中心O′1和O′2中,式(1)变为:
| $ \left[ {\begin{array}{*{20}{c}} {{x_2} - {x_{O2}}}\\ {{y_2} - {y_{O2}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\Delta x}\\ {\Delta y} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} p&q\\ { - q}&p \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_1} - {x_{O1}}}\\ {{y_1} - {y_{O1}}} \end{array}} \right] $ | (10) |
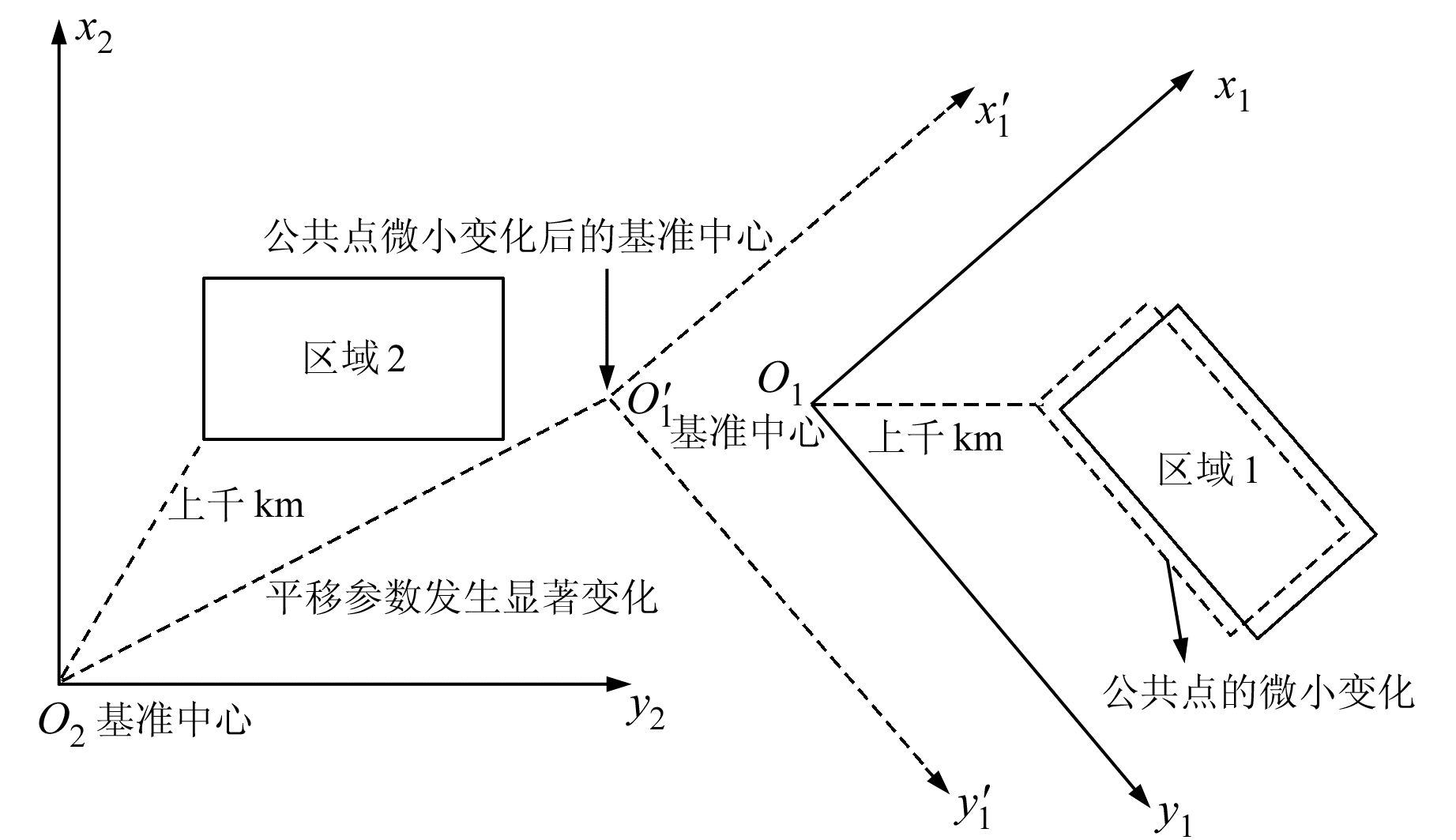
|
图 1 基准旋转中心为坐标原点 Fig. 1 Datum rotation center is the origin of coordinate system |
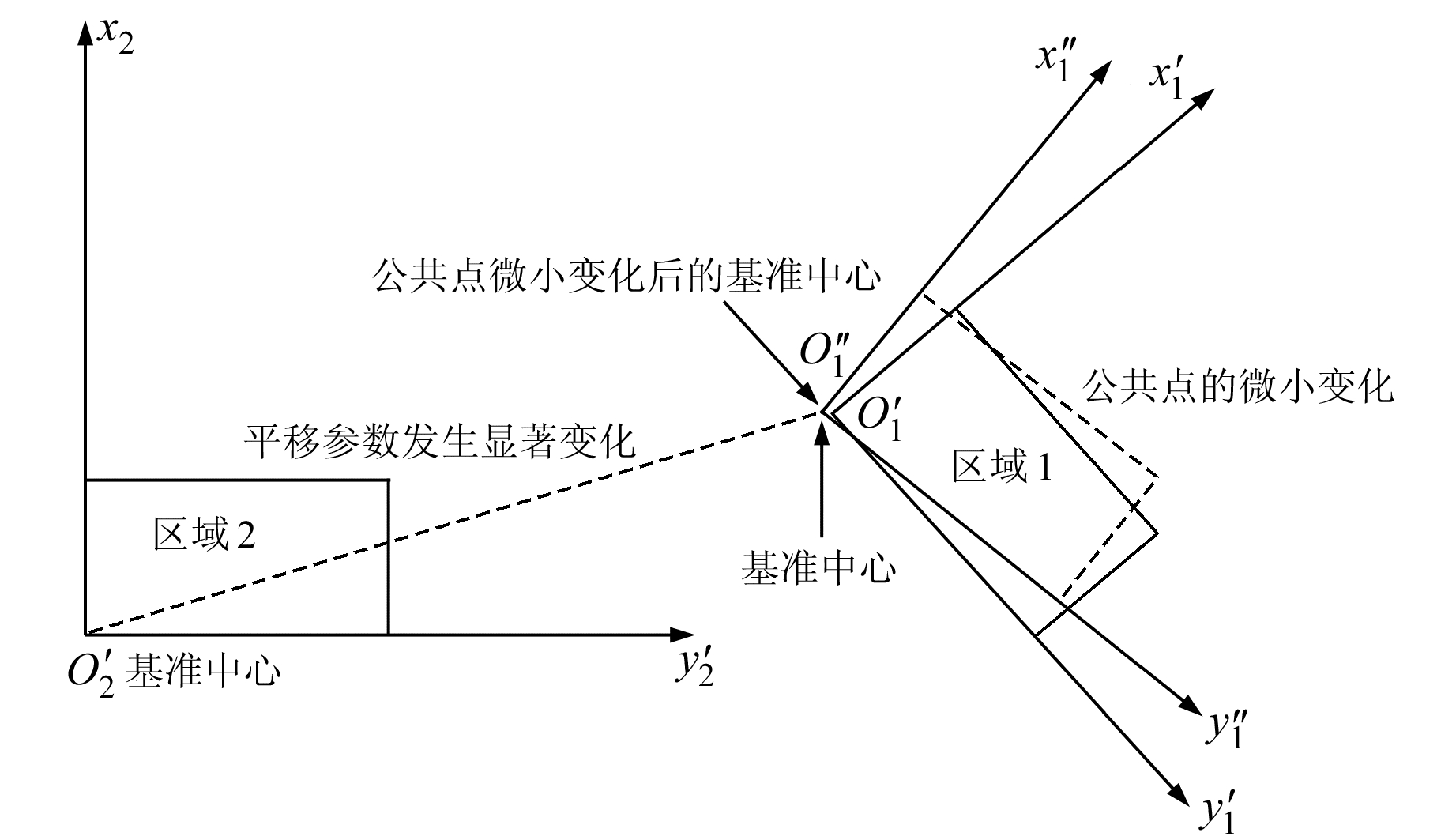
|
图 2 基准旋转中心位于转换区域 Fig. 2 Datum rotation center is located in the transformation area |
式中,(xO1, yO1)和(xO2, yO2)为x′1O′1y′1和x′2O′2y′2的基准中心坐标,矩阵形式为:
| $ \left[ {\begin{array}{*{20}{c}} {{x_2} - {x_{O2}}}\\ {{y_2} - {y_{O2}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0&{{x_1} - {x_{O1}}}&{{y_1} - {y_{O1}}}\\ 0&1&{{y_1} - {y_{O1}}}&{ - \left( {{x_1} - {x_{O1}}} \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta x}\\ {\Delta y}\\ p\\ q \end{array}} \right] $ | (11) |
由图 2看出,即使区域1中转换点产生微小变化,对坐标系x′1O′1y′1的影响并不大,再加上区域1离坐标转换的基准中心O′2的距离也大为减小,从而引起的平差参数变化也非常有限。由式(11)知,系数矩阵中元素之间的比例关系大为减小,解决了转换系数矩阵的病态性问题。
利用表 1中的算例再次进行计算,设4个转换点的平面坐标基准中心为4个公共点坐标的平均值,法方程N的条件数cond(N)=7.107 6×108,为良性。若1个公共点在1980西安坐标系的x坐标增加1 cm和2 cm,平移参数变化值最大为3 mm,见表 2。可知,当系数矩阵B中元素的差值量级减小后,即使增加较小的波动,平移参数的变化并不显著。
|
|
表 2 矩阵对参数的扰动影响 Tab. 2 Fluctuating effect of matrix on parameters |
某城市连续运行卫星定位服务综合系统CORS共有20个GPS连续运行跟踪基准站,在观测过程中实时将观测数据传输到电脑上,需要定期对观测数据进行解算,通过联合国家坐标系中的控制点,经GPS网基线解算和平差后获取20个站在国家大地坐标系的大地坐标,高斯投影得到20个GPS站在CGCS2000和1980西安坐标系的高斯平面坐标(表 3、表 4)。
|
|
表 3 1980西安坐标系中的高斯平面坐标 Tab. 3 Gauss plane coordinate in Xi'an 1980 coordinate system |
|
|
表 4 CGCS2000坐标系中的高斯平面坐标 Tab. 4 Gauss plane coordinate in CGCS2000 |
利用CosaGPS软件计算该区域CGCS2000→1980西安坐标系之间平面坐标的4个转换参数,分别为Δx=-2.270 m,Δy=117.190 m,α=-0.010″,k=1.000 003,将结果视为真值。表 5和表 6为根据式(7)和(11)计算的当基准旋转中心为坐标原点和坐标平均值时的转换参数,并给出法方程条件数;图 3和图 4为转换参数与真值的比较。
|
|
表 5 基准旋转中心为坐标原点时计算的转换参数 Tab. 5 Transformation parameters obtained when datum rotation center is the origin of coordinate system |
|
|
表 6 基准旋转中心位于转换区域时计算的转换参数 Tab. 6 Transformation parameters obtained when datum rotation center is located in transformation area |
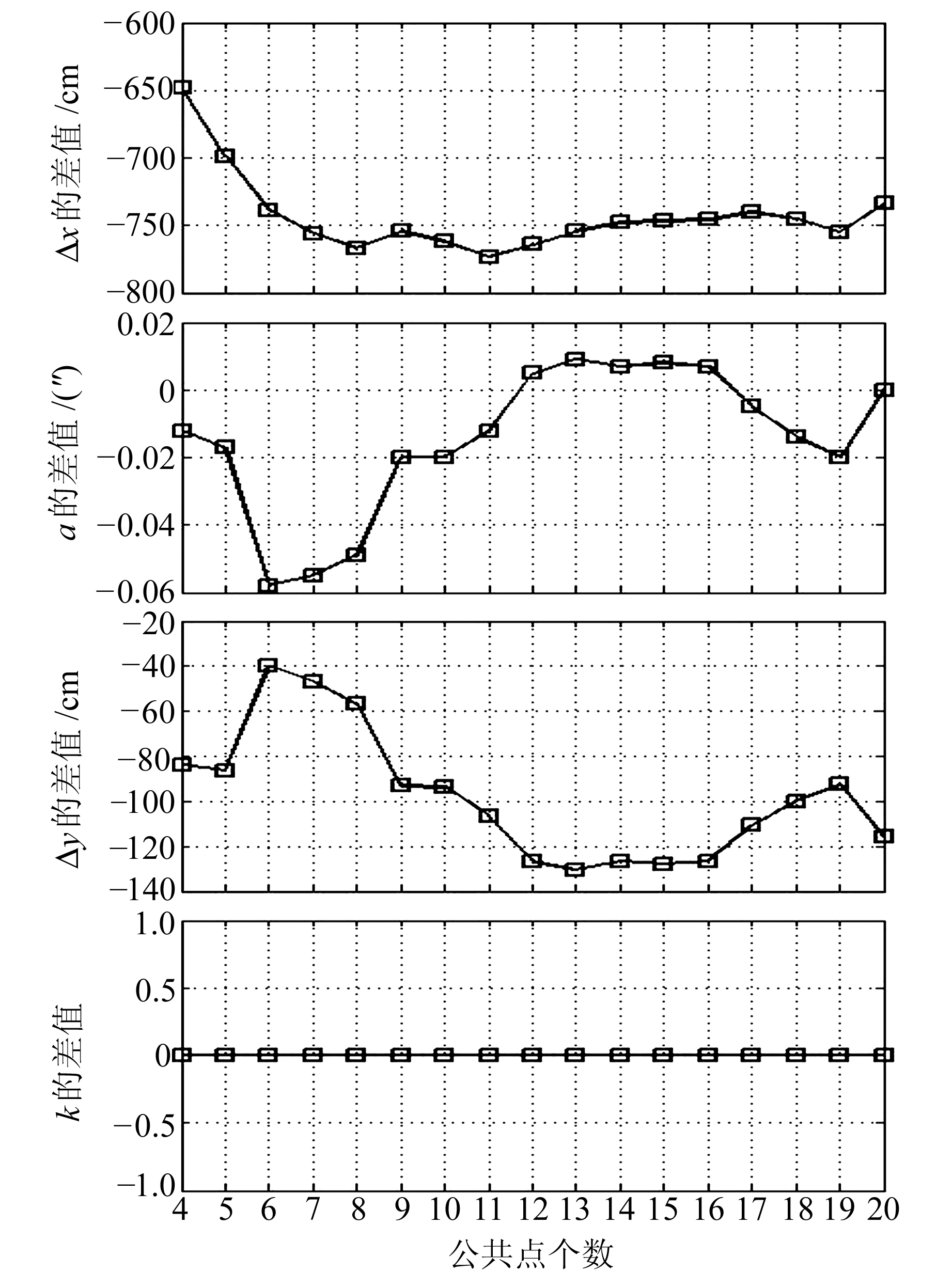
|
图 3 基准旋转中心为坐标原点时转换参数与真值的比较 Fig. 3 Comparison between transformation parameters which datum rotation center is coordinate origin and truth-values |
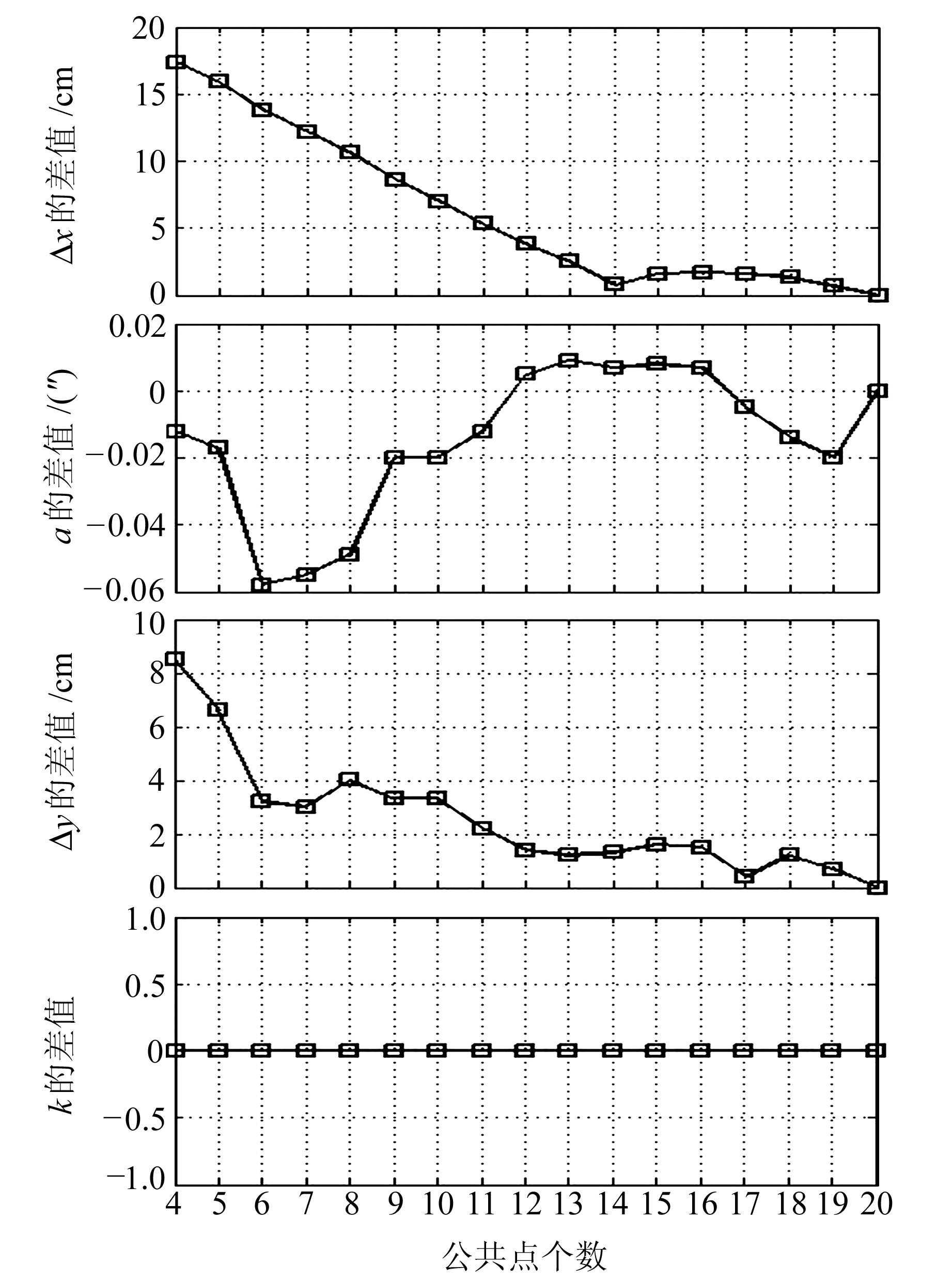
|
图 4 基准旋转中心为转换区域时转换参数与真值的比较 Fig. 4 Comparison between transformation parameters which datum rotation center is located transformation area and truth-values |
1) 当基准旋转中心为坐标原点时,平移参数与真值相差超过8 m,且条件数达到1017,为病态。当采用不同的公共点时,平移参数的差值达到-1.252 m。可见,公共点变化对转换参数有较大的影响。
2) 当基准旋转中心为转换区域时,平移参数与真值非常接近,且条件数最大为109,为良性。随意选取4个GPS站,平移参数最大相差17.4 cm,公共点变化对转换参数的影响有限,且选择部分公共点或所有公共点时,转换参数值均比较稳定。
3) 当基准旋转中心位于坐标原点和转换区域时,旋转角度α和尺度参数k均几乎相等,且与真值相比,α差值最大为0.06″,k几乎无差别,影响主要体现在平移参数上。
5 结语将基准旋转中心引入平面坐标转换模型后,大大减弱了法方程列向量之间的相关性,解决了转换系数矩阵病态的问题,得到的坐标转换参数可靠。无论是采用部分公共点还是所有公共点,求解出的转换参数均具有较好的稳定性。
| [1] |
施一民, 朱紫阳, 宋树军. 不同的新型大地坐标系之间的坐标转换[J]. 同济大学学报:自然科学版, 2008, 36(7): 977-980 (Shi Yimin, Zhu Ziyang, Song Shujun. Coordinate Transformation between New Forms of Geodetic Coordinate Systems[J]. Journal of Tongji University:Natural Science, 2008, 36(7): 977-980)
(  0) 0) |
| [2] |
曾文宪, 陶本藻. 三维坐标转换的非线性模型[J]. 武汉大学学报:信息科学版, 2003, 28(5): 566-568 (Zeng Wenxian, Tao Benzao. Non-Linear Adjustment Model of Three Dimensional Coordinate Transformation[J]. Geomatics and Information Science of Wuhan University, 2003, 28(5): 566-568)
(  0) 0) |
| [3] |
刘陶胜, 黄声享, 罗力, 等. 基于重心基准的平面坐标转换研究[J]. 大地测量与地球动力学, 2011, 31(2): 102-106 (Liu Taosheng, Huang Shengxiang, Luo Li, et al. On Plane Coordinate Transformation Based on Barycentre Datum[J]. Journal of Geodesy and Geodynamics, 2011, 31(2): 102-106)
(  0) 0) |
| [4] |
沈云中, 胡雷鸣, 李博峰. Bursa模型用于局部区域坐标变换的病态问题及其解法[J]. 测绘学报, 2006, 35(2): 94-98 (Shen Yunzhong, Hu Leiming, Li Bofeng. Ill-Posed Problem in Determination of Coordinate Transformation Parameter with Small Areas Data Based on Bursa Model[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(2): 94-98)
(  0) 0) |
| [5] |
杨娟, 黄淑玲, 戴洪宝, 等. 平面坐标转换模型的病态性分析与正则化算法[J]. 测绘科学, 2015, 40(6): 21-60 (Yang Juan, Huang Shuling, Dai Hongbao, et al. Reaserch on Ill-Conditioned Problem in Plane Coordinate Conversion Model and Its Regularization Algorithm[J]. Science of Surveying and Mapping, 2015, 40(6): 21-60)
(  0) 0) |
| [6] |
孙献. 数值线性代数讲义[M]. 天津: 南开大学出版社, 1987 (Sun Xian. Handout of Numerical Linear Algebra[M]. Tianjin: Nankai University Press, 1987)
(  0) 0) |
2. Rows 247 of Hunan Non-Ferrous Metals Geology Investigation Bureau, 100 Dongliu Road, Changsha 410129, China
 2018, Vol. 38
2018, Vol. 38

