2. 中国科学院大学,北京市玉泉路19号(甲),100049;
3. 中国科学院精密导航定位与定时技术重点实验室,西安市书院东路3号,710600;
4. 长安大学地质工程与测绘学院,西安市雁塔路126号,710054
北斗卫星导航系统(BDS)第2阶段于2012-12-27建设完成,正式为亚太区域用户提供导航、定位、授时以及短报文通信服务[1]。北斗二代卫星导航系统目前提供正常服务的卫星共有14颗,分别为5颗GEO卫星(C01~C05)、6颗IGSO卫星(C06~C10、C13)以及3颗MEO卫星(C11、C12、C14)[2]。
精确的卫星轨道是导航系统提供正常服务的前提,而精确的卫星动力学模型是卫星获取高精度定轨结果的重要因素[3]。目前,GPS卫星的动力学模型已较为成熟,但对于BDS而言,部分动力学模型不再适用。例如,BDS在卫星姿态控制方面与GPS等导航系统存在较大差异,相比于GPS卫星的动偏姿态控制模式,BDS中GEO卫星采用零偏的姿态控制模式,IGSO卫星与MEO卫星采用动偏和零偏相互切换的姿态控制模式[4],BDS这种独特的姿态控制模式使得目前的动力学模型很难准确模拟卫星的运动状态,导致BDS卫星定轨精度较低。通过某种手段补偿未被模型化的误差是一种有效方法。目前,有多种动力学模型的补偿方法,其中Beutler等[5]于1994年提出在动力学定轨中加入伪随机脉冲参数补偿力模型不准确的方法后,被广泛应用于导航卫星定轨以及低轨卫星定轨当中,其实现手段为:在定轨弧段特定时刻分别对卫星在轨道切向、法向和径向施加一个速度增量,使后续的轨道发生变化,以此来补偿动力学模型的精度以及长时段数值积分带来的精度损失[6-13]。
针对BDS动力学模型精度较低的问题,多位学者已利用附加伪随机脉冲参数或轨道切向经验常量加速度的策略来提高BDS卫星的定轨精度,尤其是对于零偏状态下的BDS卫星[4, 14-18],但对于伪随机脉冲参数估计间隔对BDS 3类卫星定轨精度的影响并未进行详细讨论。基于此,本文在附加伪随机脉冲参数的动力学定轨方法的基础上,在BDS定轨过程中加入不同时间间隔的伪随机脉冲参数,分析常规状态下伪随机脉冲参数对定轨精度的影响,并着重分析在动偏转零偏状态以及进入地影状态下伪随机脉冲参数对相应卫星定轨精度的影响。
1 附加伪随机脉冲参数的动力学定轨方法对于BDS等导航卫星,动力学定轨法基本过程分为[19]:
1) 建立卫星受摄运动方程。卫星在太空中运动除受到地球中心引力影响外,还受到各种摄动力的影响。某一时刻卫星受到的力可用卫星的动力学参数(位置、速度和光压)表示:
| $ \mathit{m}\mathit{\boldsymbol{a}}{\rm{ }}\left( \mathit{t} \right){\rm{ = }}\mathit{f}\left( {{\rm{ }}\mathit{\boldsymbol{M}}{\rm{, }}\mathit{t}} \right) $ | (1) |
式中,m表示卫星质量,a(t)为t时刻的卫星加速度向量,f为卫星在轨运动受到的力函数,M为t时刻卫星动力学参数向量。
2) 求解卫星受摄运动方程。通常采用数值积分方法对方程进行解算,整个定轨弧段各历元时刻卫星的位置均可用初始时刻的卫星动力学参数表示:
| $ \mathit{\boldsymbol{y}}{\rm{ }}\left( \mathit{t} \right){\rm{ = }}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\rm{ (}}\mathit{t}{\rm{, }}{\mathit{t}_{\rm{0}}}{\rm{) }}\mathit{\boldsymbol{M}}{{\rm{}}_{\rm{0}}} $ | (2) |
式中,y为t时刻的卫星位置向量,Φ(t, t0)为t时刻相对于t0时刻的状态转移矩阵,M0为初始时刻的动力学参数向量。
3) 根据地面跟踪站观测数据建立观测方程,并对其进行求解。本文基于非差观测模型,采用BDS/GPS联合定轨的策略对BDS卫星轨道进行求解。在联合定轨时,同一时刻每个系统的接收机钟差是不同的,它们之间相差一个接收机系统间偏差参数[20]。本文选取GPS为基准系统。GPS伪距和载波观测模型为:
| $ \begin{array}{l} \mathit{P}_{{\rm{g, }}\mathit{j}{\rm{, }}\mathit{f}}^\mathit{i}{\rm{ = }}\mathit{\rho }_\mathit{j}^i{\rm{ + }}\mathit{c}{\rm{(d}}{\mathit{t}_{{\rm{g, }}\mathit{j}}}{\rm{ - d}}{\mathit{T}^\mathit{i}}{\rm{) + d}}_{{\rm{ion}}\mathit{j}}^\mathit{i}{\rm{ + }}\\ \;\;\;\mathit{d}_{{\rm{tro}}\mathit{j}}^\mathit{i}{\rm{ + (}}{\mathit{d}_{{\rm{g, }}\mathit{j}{\rm{, }}\mathit{f}}}{\rm{ - }}\mathit{d}_{{\rm{g, }}\mathit{f}}^\mathit{i}{\rm{) + }}{\mathit{d}_{{\rm{atx}}\mathit{j}}}{\rm{ + }}{\mathit{\varepsilon }_{\mathit{P}{\rm{g}}}} \end{array} $ | (3) |
| $ \begin{array}{l} \mathit{\Phi }_{{\rm{g, }}\mathit{j}{\rm{, }}\mathit{f}}^\mathit{i}{\rm{ = }}\mathit{\rho }_\mathit{j}^i{\rm{ + }}\mathit{c}{\rm{(d}}{\mathit{t}_{{\rm{g, }}\mathit{j}}}{\rm{ - d}}{\mathit{T}^\mathit{i}}{\rm{) - }}\mathit{d}_{{\rm{ion}}\mathit{j}}^\mathit{i}{\rm{ + }}\;\mathit{d}_{{\rm{tro}}\mathit{j}}^\mathit{i}{\rm{ + }}\\ {\rm{(}}{\mathit{\delta }_{{\rm{g, }}\mathit{j}{\rm{, }}\mathit{f}}}{\rm{ - }}\mathit{\delta }_{{\rm{g, }}\mathit{f}}^\mathit{i}{\rm{) + }}\mathit{\lambda }{\rm{(}}\mathit{a}_{{\rm{g, }}\mathit{j}{\rm{, }}\mathit{f}}^\mathit{i}{\rm{ + }}{\mathit{\delta }_\mathit{\varphi }}_{{\rm{g, }}\mathit{j}{\rm{, }}\mathit{f}}{\rm{ + }}\mathit{\delta }_{\mathit{\varphi }{\rm{g, }}\mathit{f}}^\mathit{i}{\rm{)}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{d}_{{\rm{atx}}\mathit{j}}}{\rm{ + }}{\mathit{\varepsilon }_{\mathit{\Phi }{\rm{g}}}} \end{array} $ | (4) |
BDS伪距和载波观测模型为:
| $ \begin{array}{l} \mathit{P}_{{\rm{b, }}\mathit{j}{\rm{, }}\mathit{f}}^\mathit{i}{\rm{ = }}\mathit{\rho }_\mathit{j}^i{\rm{ + }}\mathit{c}{\rm{(d}}{\mathit{t}_{{\rm{g, }}\mathit{j}}}{\rm{ - d}}{\mathit{T}^\mathit{i}}{\rm{) + }}\mathit{c}{\rm{\Delta }}{\mathit{t}_\mathit{j}}{\rm{ + }}\mathit{d}_{{\rm{ion}}\mathit{j}}^\mathit{i}{\rm{ + }}\\ \;\;\;\;\;\;\;\;\mathit{d}_{{\rm{tro}}\mathit{j}}^\mathit{i}{\rm{ + (}}{\mathit{d}_{{\rm{b, }}\mathit{j}{\rm{, }}\mathit{f}}}{\rm{ - }}\mathit{d}_{{\rm{b, }}\mathit{f}}^\mathit{i}{\rm{) + }}{\mathit{d}_{{\rm{atx}}\mathit{j}}}{\rm{ + }}{\mathit{\varepsilon }_{\mathit{P}{\rm{b}}}} \end{array} $ | (5) |
| $ \begin{array}{l} \mathit{\Phi }_{{\rm{b, }}\mathit{j}{\rm{, }}\mathit{f}}^\mathit{i}{\rm{ = }}\mathit{\rho }_\mathit{j}^i{\rm{ + }}\mathit{c}{\rm{(d}}{\mathit{t}_{{\rm{g, }}\mathit{j}}}{\rm{ - d}}{\mathit{T}^\mathit{i}}{\rm{) + }}\mathit{c}{\rm{\Delta }}{\mathit{t}_\mathit{j}}\mathit{ - }\\ \;\;\;\;\;\;\;\;\mathit{d}_{{\rm{ion}}\mathit{j}}^\mathit{i}{\rm{ + }}\mathit{d}_{{\rm{tro}}\mathit{j}}^\mathit{i}{\rm{ + (}}{\mathit{\delta }_{{\rm{b, }}\mathit{j}{\rm{, }}\mathit{f}}}{\rm{ - }}\mathit{\delta }_{{\rm{b, }}\mathit{f}}^\mathit{i}{\rm{) + }}\\ \mathit{\lambda }{\rm{(}}\mathit{a}_{{\rm{b, }}\mathit{j}{\rm{, }}\mathit{f}}^\mathit{i}{\rm{ + }}{\mathit{\delta }_\mathit{\varphi }}_{{\rm{b, }}\mathit{j}{\rm{, }}\mathit{f}}{\rm{ + }}\mathit{\delta }_{\mathit{\varphi }{\rm{b, }}\mathit{f}}^\mathit{i}{\rm{) + }}{\mathit{d}_{{\rm{atx}}\mathit{j}}}{\rm{ + }}{\mathit{\varepsilon }_{\mathit{\Phi }{\rm{b}}}} \end{array} $ | (6) |
式中,Pg, j, fi和Φg, j, fi分别为GPS的伪距和载波相位观测量(单位m),Pb, j, fi和Φb, j, fi分别为BDS的伪距和载波相位观测量,ρji为卫星和测站间的几何距离,c为光速,dtg, j为GPS信号的接收机钟差,dTi为卫星钟差,Δtj为接收机系统间偏差,dionji为电离层延迟,dtroji为对流层延迟,dg, j, f和dg, fi分别为GPS接收机和卫星端的码硬件延迟,db, j, f和db, fi分别为BDS接收机和卫星端的码硬件延迟,δg, j, f和δg, fi分别为GPS接收机和卫星端的相位硬件延迟,δb, j, f和δb, fi分别为BDS接收机和卫星端的相位硬件延迟,λ为载波波长,ag, j, fi和ab, j, fi分别为GPS和BDS的整周模糊度,δφg, j, f和δφg, fi分别为GPS接收机和卫星端的初始相位,δφb, j, f和δφb, fi分别为BDS接收机和卫星端的初始相位,datxj为天线相位中心改正,εPg和εΦg分别为GPS的剩余误差,εPb和εΦb分别为BDS的剩余误差。
4) 固定模糊度,得到固定解。对式(3)~(6)进行迭代求解,当残差小于阈值时停止迭代;然后对观测值组双差,固定模糊度,通过参数估计得到精确的初始时刻动力学参数。
5) 计算最终定轨结果。由式(2)及第4)步得到的初始时刻动力学参数,计算各历元时刻卫星位置。
当动力学模型精度较低,不足以描述卫星轨道的变化规律时,可通过伪随机脉冲参数进行补偿,由于其具有瞬时、随机等特性,需要进行单独估计。式(2)可表示为[21]:
| $ \mathit{y}\left( \mathit{t} \right){\rm{ = }}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\rm{ (}}\mathit{t}{\rm{, }}{\mathit{t}_{\rm{0}}}{\rm{) }}\mathit{\boldsymbol{M}}{{\rm{}}_{\rm{0}}}{\rm{ + }}\mathit{\boldsymbol{V}}{{\rm{}}_{\mathit{b}{\rm{(}}\mathit{t}{\rm{)}}}} $ | (7) |
式中,Vb(t)为t时刻的伪随机脉冲参数引起的卫星轨道变化,该参数的性质类似于分段常参数[21],对估计历元以及后续历元有效,独立于数值积分过程。此时,式(3)~(6)在计算卫星和测站间的几何距离(ρji)时,卫星的位置可根据式(7)由初始时刻动力学参数、状态转移矩阵以及伪随机脉冲参数表示,则伪随机脉冲参数可在参数估计时进行求解,得到附加伪随机脉冲参数修正的定轨结果。目前,BDS卫星定轨通常采用3 d解的定轨策略,在整个定轨弧段中应估计多组伪随机脉冲参数。图 1给出了定轨流程。

|
图 1 附加伪随机脉冲参数的动力学定轨流程 Fig. 1 Process of dynamic orbit determination which adds the pseudo-stochastic pulse parameters |
选取MGEX网络65个跟踪站的观测数据,定轨策略为BDS/GPS一步法联合定轨(表 1)。在评价轨道精度时采用重叠弧段的比较策略,即将前一个3 d解中第3天的定轨结果与后一个3 d解中第2天的定轨结果进行比较。
|
|
表 1 定轨数据处理策略 Tab. 1 Data processing strategies of orbit determination |
为了分析伪随机脉冲参数对BDS定轨的影响,采用4种方案,分别为每6 h、12 h、24 h估计一组和不估计伪随机脉冲参数。首先,利用2016年年积日208~225的观测数据给出在BDS卫星常规状态下(GEO卫星为零偏状态,IGSO卫星和MEO卫星为动偏状态)伪随机脉冲参数对其定轨精度的影响,结果如表 2和图 2所示。其次,利用2016年年积日204~207的观测数据给出在动偏转零偏状态下,伪随机脉冲参数对相应卫星(C07和C10)定轨精度的整体影响,结果如图 3所示。最后,利用2016年年积日208~216的观测数据给出在进入地影状态下伪随机脉冲参数对相应卫星(C07和C10)定轨精度的整体影响,结果如图 4所示。
|
|
表 2 常规状态下伪随机脉冲参数对BDS卫星定轨精度的影响 Tab. 2 Impact of pseudo-stochastic pulse parameters on the orbit determination precisions of BDS satellites under the normal status |

|
图 2 常规状态下伪随机脉冲参数对BDS卫星定轨平均精度的影响 Fig. 2 Impact of pseudo-stochastic pulse parameters on the orbit determination average precisions of BDS satellites under the normal status |
|
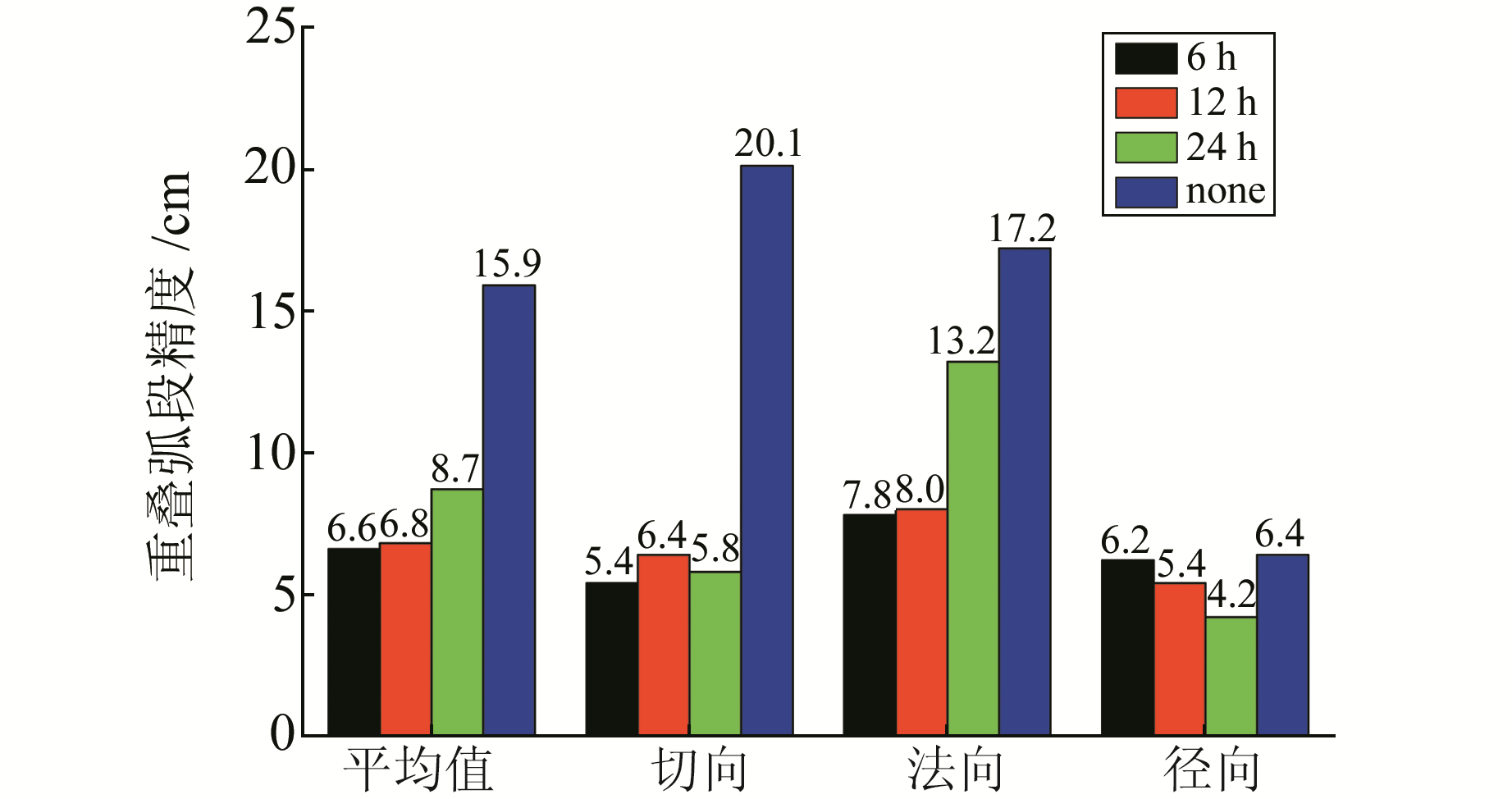
图 3 动偏转零偏状态下伪随机脉冲参数对C07和C10卫星定轨精度的影响 Fig. 3 Impact of pseudo-stochastic pulse parameters on the orbit determination precisions of the C07 and C10 satellites under the yaw attitude maneuver status |
|
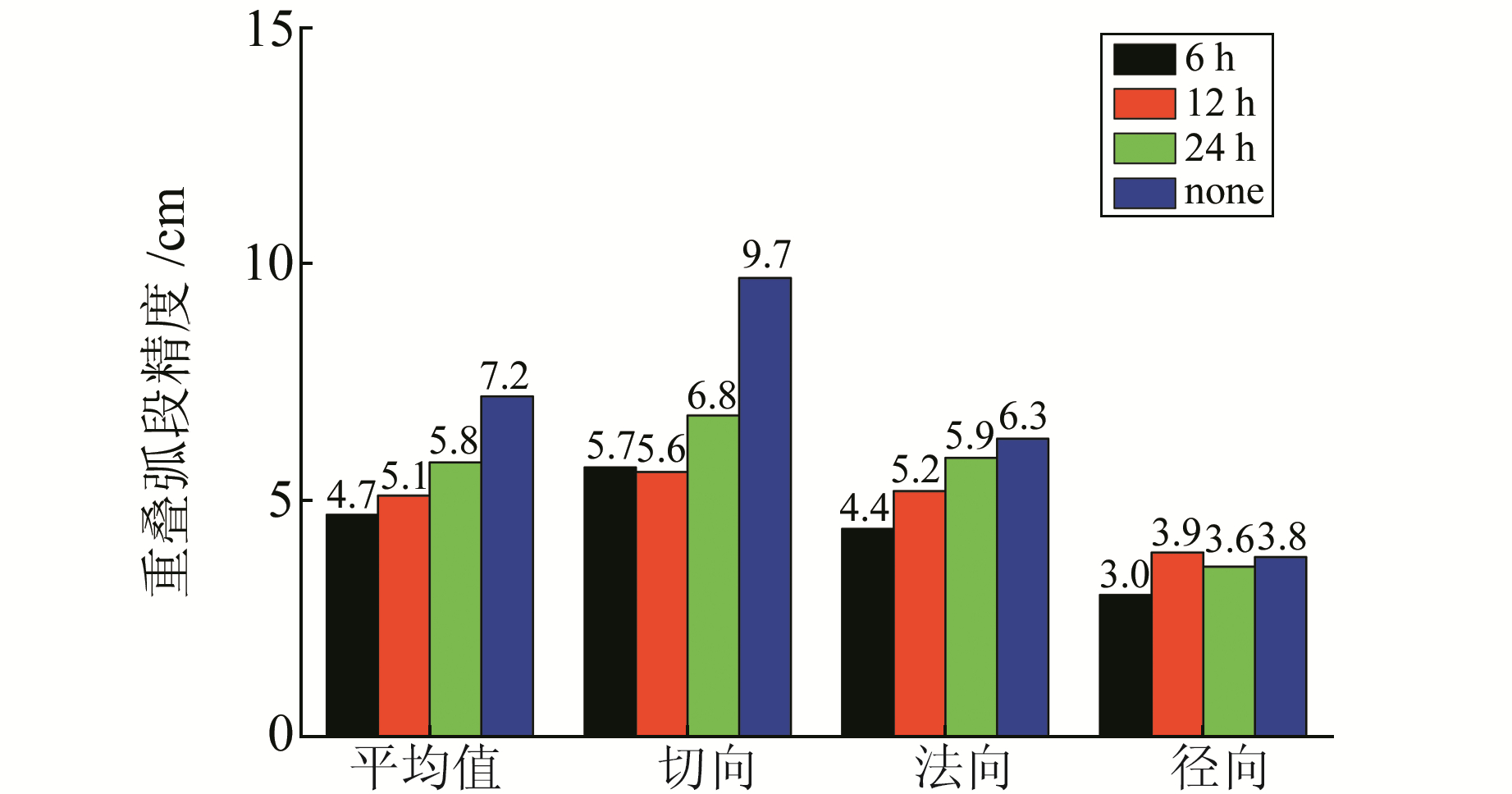
图 4 进入地影状态下伪随机脉冲参数对C07和C10卫星定轨精度的影响 Fig. 4 Impact of pseudo-stochastic pulse parameters on the orbit determination precisions of the C07 and C10 satellites under the shadow running status |
由图 2看出,在常规状态下,不同间隔的伪随机脉冲参数对GEO卫星3个方向的定轨精度均改善显著,而对IGSO、MEO卫星并不显著,主要是由于GEO卫星采用零偏的姿态控制模式。对于GEO、IGSO及MEO卫星,最优的估计间隔分别为24 h、24 h和12 h,3类卫星伪随机脉冲参数最优的估计间隔与其运行周期一致,较好地补偿了各类卫星周期性的误差。
由图 3和图 4看出,伪随机脉冲参数对动偏转零偏及进入地影状态下的卫星定轨精度改善显著,尤其在轨道切向和法向,主要是由于相对于径向,切向和法向更难用力模型模拟。对于两种状态下的卫星,6 h间隔的伪随机脉冲参数定轨结果均为最优,主要是由于光压模型不能很好地描述零偏姿态卫星状态,相对于12 h和24 h,更高频率的6 h伪随机脉冲参数估计间隔较好地补偿了未被精确模型化的动力学模型误差。
3 结语在附加伪随机脉冲参数的动力学定轨方法的基础上,分析了BDS卫星在常规状态、动偏转零偏状态以及进入地影状态下,不同估计间隔的伪随机脉冲参数对BDS卫星定轨精度的影响。
1) 伪随机脉冲参数对提高当前BDS卫星定轨精度有一定的贡献,其中对GEO卫星定轨精度的改善尤为显著,其与卫星运行周期相关。
2) 对于动偏转零偏以及进入地影状态下的卫星,6 h的伪随机脉冲参数估计较好地吸收了未被模型化的误差,能够改善定轨精度,可为今后BDS卫星精密定轨提供参考。
致谢 感谢全球连续监测评估系统(iGMAS)及MGEX跟踪站网络提供数据,感谢GFZ葛茂荣教授对本文提供支持。
| [1] |
Yang Y X, Li J L, Wang A B, et al. Preliminary Assessment of the Navigation and Positioning Performance of Beidou Regional Navigation Satellite System[J]. Science China Earth Sciences, 2014, 57(1): 144-152 DOI:10.1007/s11430-013-4769-0
(  0) 0) |
| [2] |
张睿, 杨元喜, 张勤, 等. BDS卫星动力学参数最优解与定轨跟踪站最优分布[J]. 大地测量与地球动力学, 2016, 36(3): 216-220 (Zhang Rui, Yang Yuanxi, Zhang Qin, et al. Optimal Estimation of Dynamic Parameters of BDS Orbit for Optimally Selection of Tracking Stations[J]. Journal of Geodesy and Geodynamics, 2016, 36(3): 216-220)
(  0) 0) |
| [3] |
Zhang R, Zhang Q, Huang G, et al. Impact of Tracking Station Distribution Structure on Beidou Satellite Orbit Determination[J]. Advances in Space Research, 2015, 56(10): 2 177-2 187 DOI:10.1016/j.asr.2015.07.045
(  0) 0) |
| [4] |
郭靖. 姿态、光压和函数模型对导航卫星精密定轨影响的研究[D]. 武汉: 武汉大学, 2014 (Guo Jing. The Impacts of Attitude, Solar Radiation and Function Model on Precise Orbit Determination for GNSS Satellites[D]. Wuhan: Wuhan University, 2014) http://cdmd.cnki.com.cn/Article/CDMD-10486-1015528772.htm
(  0) 0) |
| [5] |
Beutler G, Brockmann E, Gurtner W, et al. Extended Orbit Modeling Techniques at the CODE Processing Center of the International GPS Service for Geodynamics (IGS): Theory and Initial Results[J]. Manuscr Geod, 1994, 19: 367-384
(  0) 0) |
| [6] |
Springer T A, Beutler G, Rothacher M. Improving the Orbit Estimates of GPS Satellites[J]. Journal of Geodesy, 1999, 73(3): 147-157 DOI:10.1007/s001900050230
(  0) 0) |
| [7] |
Vehla D, Rothacher M. Kinematic and Reduced-Dynamic Precise Orbit Determination of Low Earth Orbiters[J]. Advances in Geosciences, 2003(1): 47-56
(  0) 0) |
| [8] |
刘经南, 赵齐乐, 张小红. CHAMP卫星的纯几何定轨及动力平滑中的动力模型补偿研究[J]. 武汉大学学报:信息科学版, 2004, 29(1): 1-6 (Liu Jingnan, Zhao Qile, Zhang Xiaohong. Geometric Orbit Determination of CHAMP Satellite and Dynamic Models' Compensation During Orbit Smoothing[J]. Geomatics and Information Science of Wuhan University, 2004, 29(1): 1-6)
(  0) 0) |
| [9] |
韩保民, 朱秀英, 柳林涛, 等. 伪随机脉冲估计及其在简化动力学定轨中的应用[J]. 武汉大学学报:信息科学版, 2007, 32(5): 466-469 (Han Baomin, Zhu Xiuying, Liu Lintao, et al. Estimation of Pseudo-Stochastic Pulses and Their Applications in Reduced-Dynamic Orbit Determination[J]. Geomatics and Information Science of Wuhan University, 2007, 32(5): 466-469)
(  0) 0) |
| [10] |
韩保民. 基于星载GPS双频观测值的简化动力学定轨方法[J]. 南京航空航天大学学报, 2007, 39(2): 149-153 (Han Baomin. Reduced-Dynamic Orbit Determination Using Dual-Frequency Onboard GPS Observations[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2007, 39(2): 149-153)
(  0) 0) |
| [11] |
赵春梅, 程鹏飞, 益鹏举. 基于伪随机脉冲估计的简化动力学卫星定轨方法[J]. 宇航学报, 2011, 32(4): 762-766 (Zhao Chunmei, Cheng Pengfei, Yi Pengju. Reduced-Dynamics Satellite Orbit Determination Based on Pseudo-Stochastic Pulse Estimation[J]. Journal of Astronautics, 2011, 32(4): 762-766)
(  0) 0) |
| [12] |
张兵兵. 随机脉冲对简化动力学定轨影响分析[D]. 淄博: 山东理工大学, 2014 (Zhang Bingbing. Stochastic Pulses and the Effect in Reduced-Dynamics Orbit[D]. Zibo: Shandong University of Technology, 2014) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D570172
(  0) 0) |
| [13] |
刘伟平, 郝金明, 田英国, 等. 一种伪随机脉冲的快速参数估计方法[J]. 武汉大学学报:信息科学版, 2015, 40(11): 1 487-1 482 (Liu Weiping, Hao Jinming, Tian Yingguo, et al. Fast Parameter Estimation for Pseudo-Stochastic Pulse[J]. Geomatics and Information Science of Wuhan University, 2015, 40(11): 1 487-1 482)
(  0) 0) |
| [14] |
Guo J, Xu X L, Zhao Q L, et al. Precise Orbit Determination for Quad-Constellation Satellites at Wuhan University: Strategy, Result Validation, and Comparison[J]. Journal of Geodesy, 2016, 90(2): 143-159 DOI:10.1007/s00190-015-0862-9
(  0) 0) |
| [15] |
Guo J, Zhao Q L, Geng T, et al. Precise Orbit Determination for Compass IGSO Satellites during Yaw Maneuvers[C]. China Satellite Navigation Conference(CSNC) 2013, Berlin, 2013
(  0) 0) |
| [16] |
Wang W, Chen G C, Guo S R, et al. A Study on the Beidou IGSO/MEO Satellite Orbit Determination and Prediction of the Different Yaw Control Mode[C]. China Satellite Navigation Conference(CSNC) 2013, Berlin, 2013
(  0) 0) |
| [17] |
Zhu J, Wang J S, Zeng G, et al. Precise Orbit Determination of Beidou Regional Navigation Satellite System Via Double-Difference Observations[C]. China Satellite Navigation Conference(CSNC) 2013, Berlin, 2013
(  0) 0) |
| [18] |
He L N, Ge M R, Wang J X, et al. Experimental Study on the Precise Orbit Determination of the Beidou Navigation Satellite System[J]. Sensors, 2013, 13(3): 2 911-2 928 DOI:10.3390/s130302911
(  0) 0) |
| [19] |
张睿. BDS精密定轨关键技术研究[D]. 西安: 长安大学, 2016 (Zhang Rui. Research on Key Technologies of BDS Precise Orbit Determination[D]. Xi'an: Chang'an University, 2016) http://cdmd.cnki.com.cn/article/cdmd-90008-2007051628.htm
(  0) 0) |
| [20] |
黄观文. GNSS星载原子钟质量评价及精密钟差算法研究[D]. 西安: 长安大学, 2012 (Huang Guanwen. Research on Algorithms of Precise Clock Offset and Quality Evaluation of GNSS Satellite Clock[D]. Xi'an: Chang'an University, 2012) http://cdmd.cnki.com.cn/Article/CDMD-10710-1013017231.htm
(  0) 0) |
| [21] |
任锴. 导航卫星精密定轨理论与方法研究[D]. 郑州: 信息工程大学, 2015 (Ren Kai. Researches on Theory and Methodology of Precise Orbit Determination of Navigation Satellites[D]. Zhengzhou: Information Engineering University, 2015) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D829533
(  0) 0) |
| [22] |
Dilssner F, Springer T, Schoenemann E, et al. Estimation of Satellite Antenna Phase Center Corrections for Beidou[R]. IGS Workshop, 2014
(  0) 0) |
2. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China;
3. Key Laboratory of Precision Navigation Positioning and Timing Technology, CAS, 3 East-Shuyuan Road, Xi'an 710600, China;
4. College of Geology Engineering and Geomatics, Chang'an University, 126 Yanta Road, Xi'an 710054, China
 2018, Vol. 38
2018, Vol. 38

