GNSS动态差分相对定位能获得高精度的位置信息，但是需要基准站和流动站有足够的共视卫星^[1]。在城市或山区，单GPS因为卫星信号遮挡严重，导致不能定位或者定位精度较差^[2-3]。在多遮挡环境下，可视卫星的分布不均匀，导致定位解算时观测方程的强相关性，即存在病态性^[4]，而多卫星导航系统组合是较为有效的解决方法。文献[5]提出一种新的选择参考卫星的方法，提高了多卫星组合系统在多遮挡环境下的定位可靠性。

BDS于2012年末正式运行，由14颗卫星组网并提供服务^[6-7]。在随后的几年内又先后发射了6颗卫星，截至2016-06-12，共计发射23颗卫星，其中在服役中的有19颗。BDS已具备单独定位、导航的能力^[7]，相比于GPS，其观测信号更强，可提供更稳定的码相位观测值^[8]。由于卫星轨道分布不同，能够选择的卫星高度角范围增大，扩展了可定位的区域。文献[6, 9-10]通过实测数据、文献[11]通过仿真BDS卫星星座对卫星的可见性进行分析，表明BDS卫星在亚太地域具有良好的几何覆盖范围。BDS与其他卫星系统具有良好的兼容性和互操作性，为BDS/GPS组合提供了基础^[12]。BDS/GPS组合相较于单GPS不仅能够增加卫星数目，还可以改善观测卫星的几何结构，大大降低卫星的DOP值^{[6, 9-10, 13]}，改善模糊度解算的固定率和可靠性^{[6, 14-15]}。在短基线情况下，载波相位动态差分定位的精度提高20%以上^[6]。

本文主要研究BDS/GPS组合动态差分定位算法，特别是模糊度解算部分，并基于多遮挡环境下的实测数据，用自编的动态载波相位差分定位程序验证BDS/GPS组合相对于单GPS在定位解算中的优势。

1 定位解算原理 1.1 函数模型和随机模型

载波相位观测方程为：

$ \begin{array}{*{20}{c}} {\lambda \varphi _r^s\left( {{t_r}} \right) = \rho _r^s\left( {{t_r},{t_s}} \right) - c\left( {\delta {t_r} - \delta {t_s}} \right) - \lambda N_r^s - }\\ {{\delta _{{\rm{ion}}}} + {\delta _{{\rm{trop}}}} + {\delta _{{\rm{mul}}}} + {\delta _{{\rm{rel}}}} + \varepsilon } \end{array} $

(1)

式中，λ为载波的波长，φ_r^s(t_r)为载波相位观测值，ρ_r^s(t_r, t_s)为卫星和接收机间的几何距离，c为真空中的光速，δt_r为接收机钟差，δt_s为卫星钟钟差，N_r^s为整周模糊度，δ_ion为电离层延迟，δ_trop为对流层延迟，δ_mul为多路径效应，δ_rel为相对论效应，ε为误差。

采用载波双差观测方程进行动态定位解算:

$ \begin{array}{*{20}{c}} {\lambda \nabla \Delta \varphi _{{r_{1,2}}}^{{s_{1,2}}}\left( {{t_r}} \right) = \nabla \Delta \rho _{{r_{1,2}}}^{{s_{1,2}}}\left( {{t_r},{t_{{s_{1,2}}}}} \right) - \lambda \nabla \Delta N_{{r_{1,2}}}^{{s_{1,2}}} - }\\ {\nabla \Delta {\delta _{{\rm{ion}}}} + \nabla \Delta {\delta _{{\rm{trop}}}} + \nabla \Delta {\delta _{{\rm{mul}}}} + \nabla \Delta {\delta _{{\rm{rel}}}} + \nabla \Delta \varepsilon } \end{array} $

(2)

式中，∇Δ为双差算子，r_{1, 2}分别表示基准站和流动站，s_{1, 2}分别表示r_{1, 2}同步观测的2颗卫星。简化得:

$ \begin{array}{*{20}{c}} {\lambda \nabla \Delta \varphi = \nabla \Delta \rho - \lambda \nabla \Delta N - \nabla \Delta {\delta _{{\rm{ion}}}} + \nabla \Delta {\delta _{{\rm{trop}}}} + }\\ {\nabla \Delta {\delta _{{\rm{mul}}}} + \nabla \Delta {\delta _{{\rm{rel}}}} + \nabla \Delta \varepsilon } \end{array} $

(3)

假设某一历元同步观测了n颗BDS(GPS)卫星，则误差方程为：

$ \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{BX}} - \mathit{\boldsymbol{CY}} - \mathit{\boldsymbol{L}} $

(4)

式中，V为残差；B为设计矩阵，

$ \mathit{\boldsymbol{B}} = \left( {\begin{array}{*{20}{c}} {\nabla \Delta {l_1}}&{\nabla \Delta {m_1}}&{\nabla \Delta {n_1}}\\ {\nabla \Delta {l_2}}&{\nabla \Delta {m_2}}&{\nabla \Delta {n_2}}\\ \vdots&\vdots&\vdots \\ {\nabla \Delta {l_{n - 1}}}&{\nabla \Delta {m_{n - 1}}}&{\nabla \Delta {n_{n - 1}}} \end{array}} \right), $

$ l = \frac{{\left[ {{X_{{r_2}0}} - X_0^s\left( {{t_s}} \right)} \right]}}{{\rho _{{r_2}0}^s}},m = \frac{{\left[ {{Y_{{r_2}0}} - Y_0^s\left( {{t_s}} \right)} \right]}}{{\rho _{{r_2}0}^s}}, $

$ \mathit{n}\text{= }\frac{\left[{{\mathit{Z}}_{{{\mathit{r}}_{\text{2}}}\text{0}}}\text{-}\mathit{Z}_{0}^{\mathit{s}}\left( {{\mathit{t}}_{\mathit{s}}} \right) \right]}{\mathit{\rho }_{{{\mathit{r}}_{\text{2}}}\text{0}}^{\mathit{s}}}\text{ }\!\!~\!\!\text{ }$，X_r20、Y_r20、Z_r20为流动站近似坐标，X₀^s(t_s)、Y₀^s(t_s)、Z₀^s(t_s)为卫星坐标；X为流动站坐标改正数，X=$ \left( \begin{align} &\mathit{\delta }{{\mathit{X}}_{{{\mathit{r}}_{\text{2}}}}} \\ &\mathit{\delta }{{\mathit{Y}}_{{{\mathit{r}}_{\text{2}}}}} \\ &\mathit{\delta }{{\mathit{Z}}_{{{\mathit{r}}_{\text{2}}}}} \\ \end{align} \right)$；C为设计矩阵，C= $\left( {\begin{array}{*{20}{c}} \mathit{\lambda }&{}&0\\ {}&\begin{array}{l} \mathit{\lambda }\\ \;\;\;\;\;\;\; \ddots \end{array}&{}\\ 0&\begin{array}{l} \\ \left( {\mathit{n}{\rm{ - 1}}} \right) \times \left( {\mathit{n}{\rm{ + 1}}} \right) \end{array}&\mathit{\lambda } \end{array}} \right)$；Y为双差模糊度参数向量，Y=$ \left( \begin{align} &\nabla \Delta \mathit{N}_{{{\mathit{r}}_{1, 2}}}^{{{\mathit{s}}_{\text{re}, 1}}} \\ &\nabla \Delta \mathit{N}_{{{\mathit{r}}_{1, 2}}}^{{{\mathit{s}}_{\text{re}, 2}}} \\ &\ \ \ \ \ \ \ \vdots \\ &\nabla \Delta \mathit{N}_{{{\mathit{r}}_{1, 2}}}^{{{\mathit{s}}_{\text{re}, \mathit{n}\text{-}1}}} \\ \end{align} \right)$；s_re为参考卫星；L为常数向量，L=$ \left( \begin{align} &\ \ \mathit{\lambda }\nabla \text{ }\!\!\Delta\!\!\text{ }{{\mathit{\varphi }}_{\text{1}}}\text{-}\nabla \text{ }\!\!\Delta\!\!\text{ }{{\mathit{\rho }}_{\mathit{r}\text{0, 1}}} \\ &\ \ \mathit{\lambda }\nabla \text{ }\!\!\Delta\!\!\text{ }{{\mathit{\varphi }}_{\text{2}}}\text{-}\nabla \text{ }\!\!\Delta\!\!\text{ }{{\mathit{\rho }}_{\mathit{r}\text{0, 2}}} \\ &\ \ \ \ \ \ \ \ \ \ \ \vdots \\ &\mathit{\lambda }\nabla \text{ }\!\!\Delta\!\!\text{ }{{\mathit{\varphi }}_{\mathit{n}\text{-1}}}\text{-}\nabla \text{ }\!\!\Delta\!\!\text{ }{{\mathit{\rho }}_{\mathit{r}\text{0, }\mathit{n}\text{-1}}} \\ \end{align} \right)$。

在进行BDS/GPS的组合解算时，参考卫星分别在各自系统中选取，即仅在同一系统内列立方程^[13]，并采用相同的定权方式和权重。

BDS(GPS)可列立n-1个观测方程，其权阵P是n-1阶的方阵。设协因数阵Q，矩阵F、Q′均为n-1阶的方阵，定义为：

$ \mathit{\boldsymbol{F}} = \left( {\begin{array}{*{20}{c}} {n - 1}&{ - 1}& \cdots &{ - 1}\\ { - 1}&{n - 1}& \cdots &{ - 1}\\ \vdots&\vdots&\ddots&\vdots \\ { - 1}&{ - 1}& \cdots &{n - 1} \end{array}} \right) $

(5)

$ \mathit{\boldsymbol{Q'}} = \left( {\begin{array}{*{20}{c}} {1 + \frac{{\sin \left( {{E_{{\rm{ref}}}}} \right)}}{{\sin \left( {{E_1}} \right)}}}& \cdots &1\\ \vdots&\ddots&\vdots \\ 1& \cdots &{1 + \frac{{\sin \left( {{E_{{\rm{ref}}}}} \right)}}{{\sin \left( {{E_{n - 1}}} \right)}}} \end{array}} \right) $

(6)

式中，E_ref为参考卫星的高度角，E_i为第i颗卫星的高度角，i=1, 2，…，n，且i≠ref，则：

$ \mathit{\boldsymbol{Q}} = {\mathit{\boldsymbol{F}}^{\rm{T}}}\mathit{\boldsymbol{Q'F}} $

(7)

$ \mathit{\boldsymbol{P}} = {\mathit{\boldsymbol{Q}}^{ - 1}} $

(8)

若为BDS/GPS组合，则其权阵P为：

$ \mathit{\boldsymbol{P}} = \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_{\rm{C}}}}&0\\ 0&{{\mathit{\boldsymbol{P}}_{\rm{G}}}} \end{array}} \right) $

(9)

式中，P_C和P_G分别为BDS和GPS观测方程的权阵。

1.2 动态差分后处理的关键过程

文件匹配、卫星坐标计算、误差计算、基线数据存储等数据预处理完成后，关键过程如图 1所示。

1.3 模糊度搜索Ⅰ

利用宽巷的长波长特性，可以提高模糊度解算的成功率和可靠性，缩短初始化时间^[16]。忽略式(1)的电离层延迟项，将两个载波上的相位观测值相减，得到宽巷观测方程：

$ \begin{array}{*{20}{c}} {{\lambda _W}{\varphi _W} = \rho - {\lambda _W}{N_W} - c\left( {\delta {t_r} - \delta {t_s}} \right) + {\delta _{{\rm{trop}}}} + }\\ {{\delta _{{\rm{mul}}}} + {\delta _{{\rm{rel}}}} + \varepsilon } \end{array} $

(10)

式中，φ_W=φ₁-φ₂，N_W=N₁-N₂，λ_W=c/(f₁-f₂)，f₁和f₂是两个载波的频率。经线性化后的误差方程为：

$ {\mathit{\boldsymbol{V}}_W} = \mathit{\boldsymbol{BX}} - {\mathit{\boldsymbol{C}}_W}{\mathit{\boldsymbol{Y}}_W} - {\mathit{\boldsymbol{L}}_W} $

(11)

模糊度搜索Ⅰ采用将双差宽巷模糊度的浮点解直接取整的策略，为保证模糊度固定的成功率和搜索的效率，每个模糊度取最近邻的两个整数值并与其他模糊度取值作排列组合。假设有n个模糊度，则共有2ⁿ种组合方式，将每种组合分别代入式(11)进行X的最小二乘求解，取σ最小的一种组合，并计算ratio值，ratio=$ \frac{{{\mathit{\sigma }}_{\text{次小}}}}{{{\mathit{\sigma }}_{\text{最小}}}}$。

2 多遮挡环境下BDS/GPS组合在模糊度固定可靠性上的改善

GPS和BDS的误差方程为：

$ {\mathit{\boldsymbol{V}}_{\rm{G}}} = {\mathit{\boldsymbol{B}}_{\rm{G}}}\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{C}}_{\rm{G}}}{\mathit{\boldsymbol{Y}}_{\rm{G}}} - {\mathit{\boldsymbol{L}}_{\rm{G}}} $

(12)

$ {\mathit{\boldsymbol{V}}_{\rm{C}}} = {\mathit{\boldsymbol{B}}_{\rm{C}}}\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{C}}_{\rm{C}}}{\mathit{\boldsymbol{Y}}_{\rm{C}}} - {\mathit{\boldsymbol{L}}_{\rm{C}}} $

(13)

式中，G代表GPS，C代表北斗。整理得：

$ \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{V}}_{\rm{G}}}}\\ {{\mathit{\boldsymbol{V}}_{\rm{C}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_{\rm{G}}}}&{ - {\mathit{\boldsymbol{C}}_{\rm{G}}}}&0\\ {{\mathit{\boldsymbol{B}}_{\rm{C}}}}&0&{ - {\mathit{\boldsymbol{C}}_{\rm{C}}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} \mathit{\boldsymbol{X}}\\ {{\mathit{\boldsymbol{Y}}_{\rm{G}}}}\\ {{\mathit{\boldsymbol{Y}}_{\rm{C}}}} \end{array}} \right) - \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{L}}_{\rm{G}}}}\\ {{\mathit{\boldsymbol{L}}_{\rm{C}}}} \end{array}} \right) $

(14)

令$\mathit{\boldsymbol{V}}{\rm{ = }}\left( \begin{array}{l} {\mathit{\boldsymbol{V}}_{\rm{G}}}\\ {\mathit{\boldsymbol{V}}_{\rm{C}}} \end{array} \right){\rm{}}{\rm{ }},\mathit{\boldsymbol{B}}{\rm{ = }}\left( \begin{array}{l} {\mathit{\boldsymbol{B}}_{\rm{G}}}\;\;\;\; - {\mathit{\boldsymbol{C}}_{\rm{G}}}\;\;\;\;\;\;{\rm{0}}\\ {\mathit{\boldsymbol{B}}_{\rm{C}}}\;\;\;\;\;\;{\rm{0 }}\;\;\;\; - {\mathit{\boldsymbol{C}}_{\rm{C}}} \end{array} \right){\rm{}}{\rm{ }},\mathit{\boldsymbol{\hat x}}{\rm{ = }}\left( \begin{array}{l} \mathit{\boldsymbol{X}}\\ {\mathit{\boldsymbol{Y}}_{\rm{G}}}\\ {\mathit{\boldsymbol{Y}}_{\rm{C}}} \end{array} \right){\rm{}}$，$ \mathit{\boldsymbol{l}}{\rm{ = }}\left( \begin{array}{l} {\mathit{\boldsymbol{L}}_{\rm{G}}}\\ {\mathit{\boldsymbol{L}}_{\rm{C}}} \end{array} \right){\rm{}}{\rm{ }},\mathit{\boldsymbol{P}}{\rm{ = }}\left( \begin{array}{l} {\mathit{\boldsymbol{P}}_{\rm{G}}}\;\;{\rm{0}}\\ {\rm{0}}\;\;{\rm{ }}{\mathit{\boldsymbol{P}}_{\rm{C}}} \end{array} \right)$，简化为：

$ \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{B\hat x}} - \mathit{\boldsymbol{l}} $

(15)

由B^TPV=0得法方程:

$ {\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB\hat x}} - {\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{Pl}} = 0 $

(16)

则BDS/GPS组合系统解算参数X和Y_G、Y_C的法方程系数矩阵N为：

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{N}} = {\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB = }}}\\ {\left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{B}}_{\rm{G}}^{\rm{T}}{\mathit{\boldsymbol{P}}_{\rm{G}}}{\mathit{\boldsymbol{B}}_{\rm{G}}} + \mathit{\boldsymbol{B}}_{\rm{C}}^{\rm{T}}{\mathit{\boldsymbol{P}}_{\rm{C}}}{\mathit{\boldsymbol{B}}_{\rm{C}}}}&{ - \mathit{\boldsymbol{B}}_{\rm{G}}^{\rm{T}}{\mathit{\boldsymbol{P}}_{\rm{G}}}{\mathit{\boldsymbol{C}}_{\rm{G}}}}&{ - \mathit{\boldsymbol{B}}_{\rm{C}}^{\rm{T}}{\mathit{\boldsymbol{P}}_{\rm{C}}}{\mathit{\boldsymbol{C}}_{\rm{C}}}}\\ { - \mathit{\boldsymbol{C}}_{\rm{G}}^{\rm{T}}{\mathit{\boldsymbol{P}}_{\rm{G}}}{\mathit{\boldsymbol{B}}_{\rm{G}}}}&{\mathit{\boldsymbol{C}}_{\rm{G}}^{\rm{T}}{\mathit{\boldsymbol{P}}_{\rm{G}}}{\mathit{\boldsymbol{C}}_{\rm{G}}}}&0\\ { - \mathit{\boldsymbol{C}}_{\rm{C}}^{\rm{T}}{\mathit{\boldsymbol{P}}_{\rm{C}}}{\mathit{\boldsymbol{B}}_{\rm{C}}}}&0&{\mathit{\boldsymbol{C}}_{\rm{C}}^{\rm{T}}{\mathit{\boldsymbol{P}}_{\rm{C}}}{\mathit{\boldsymbol{C}}_{\rm{C}}}} \end{array}} \right)} \end{array} $

(17)

BDS的高轨卫星居多，运行角速度较小，因此当GPS观测信息足够多时，BDS/GPS组合在模糊度解算过程中的病态性不会优于单GPS^[17]。而在多遮挡的环境下，观测到的GPS卫星数量有限，设计矩阵B_G^TP_GB_G的观测结构差，本身内部病态性严重，再与模糊度系数叠加时，更影响模糊度解算的正确性和可靠性；若加入BDS，补充了必要的观测信息，明显改善观测结构，对B_G^TP_GB_G+ B_C^TP_CB_C病态性的改善远大于前述的不利影响，可减弱模糊度解算过程中的病态性，增加解的可靠性。

在固定单历元模糊度时可能出现如下3种情况：

1) 单GPS卫星数目不满足解算条件，BDS/GPS组合可以满足，且能够固定模糊度。

2) 单GPS卫星数目满足解算条件，但因卫星结构不好，不能成功固定模糊度，而BDS/GPS组合可以固定。

3) 单GPS在某前后两段历元区间的卫星数目均满足解算条件，且两者仅有1~2颗卫星不同，但模糊度只能在其中一段区间固定；而BDS/GPS组合在两段区间没有差异，模糊度均固定。

情况1)说明，BDS/GPS组合在观测方程数目上存在优势，可保证多数情况下的连续定位解算；情况2)、3)说明，在都满足解算条件的情况下，加入BDS后增加了新的观测信息，可改善观测结构。

3 算例分析

2016-03-07在有较严重信号遮挡的学校某区域进行车载动态实验，接收机类型为NovAtel ProPak6，基准站和流动站天线类型均为Nov703GGG，采样间隔均为0.2 s。

使用IE8.60软件，采用GNSS/INS差分后处理紧组合分别对基准站和流动站GPS和BDS/GPS观测数据进行处理，并将解算的每个点的坐标作为参考值。

3.1 单历元模糊度解算性能

借鉴文献[6]中对模糊度解算性能评估的方法，进行GPS以及BDS/GPS组合两种星座条件下的单历元双差模糊度解算。采用§1.2方法进行模糊度固定，§1.2、§1.3的判别条件进行模糊度验证，统计不同截止高度角条件下的固定率和固定错误率(表 1)。

由表 1知：

1) 当卫星截止高度角较低时(＜25°)，单GPS单历元双差模糊度解算的固定率约80%，固定错误率约3.34%；随着截止高度角的增大，模糊度解算的固定率迅速下降。

2) 当BDS/GPS组合定位时，截止高度角为30°时，模糊度固定率约99%，且固定错误率小于1%；高度角升高，模糊度固定率下降，下降仅约为10%，固定错误率最大为6.45%。

可见，BDS/GPS组合对模糊度固定率和可靠性具有显著贡献。

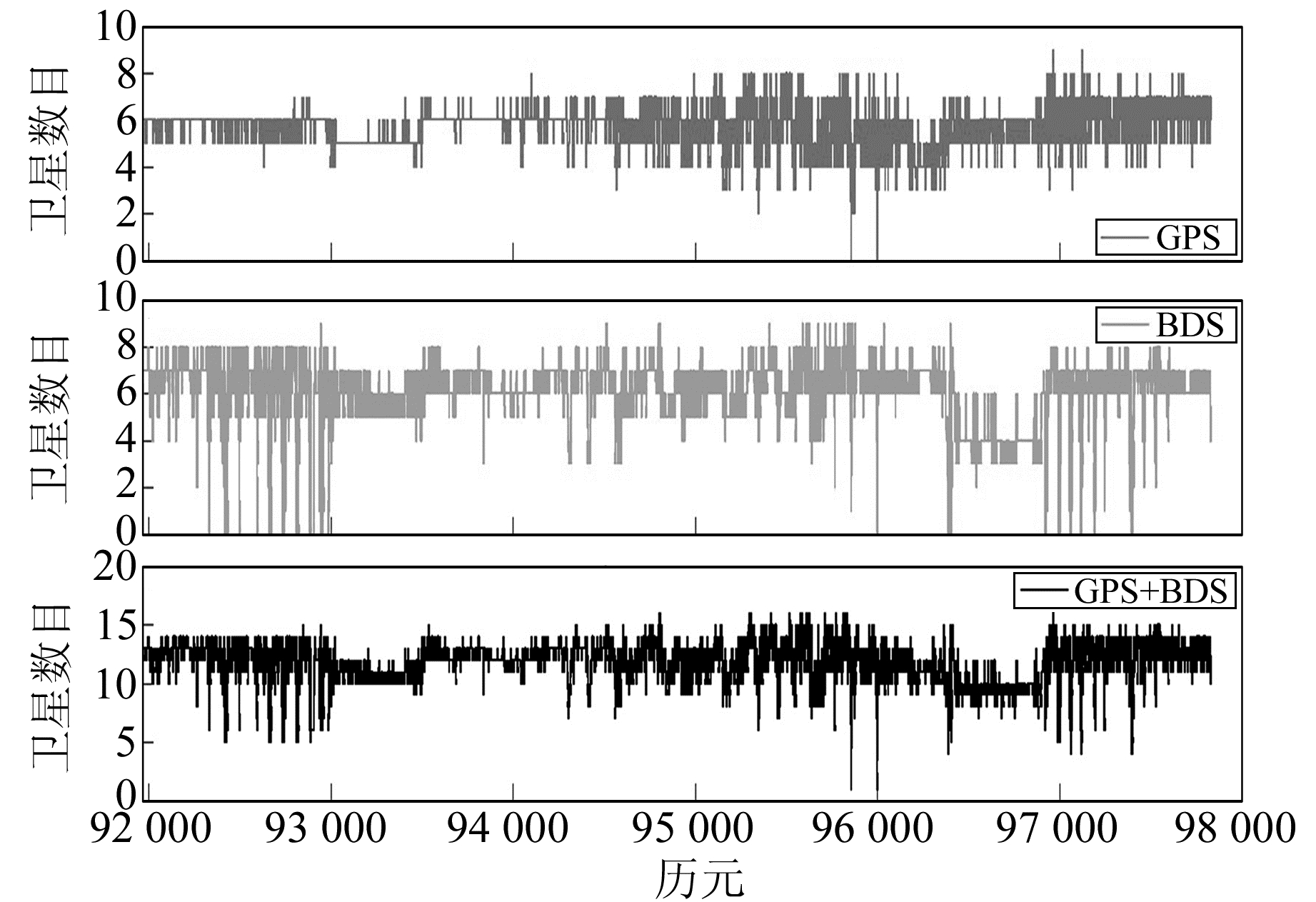
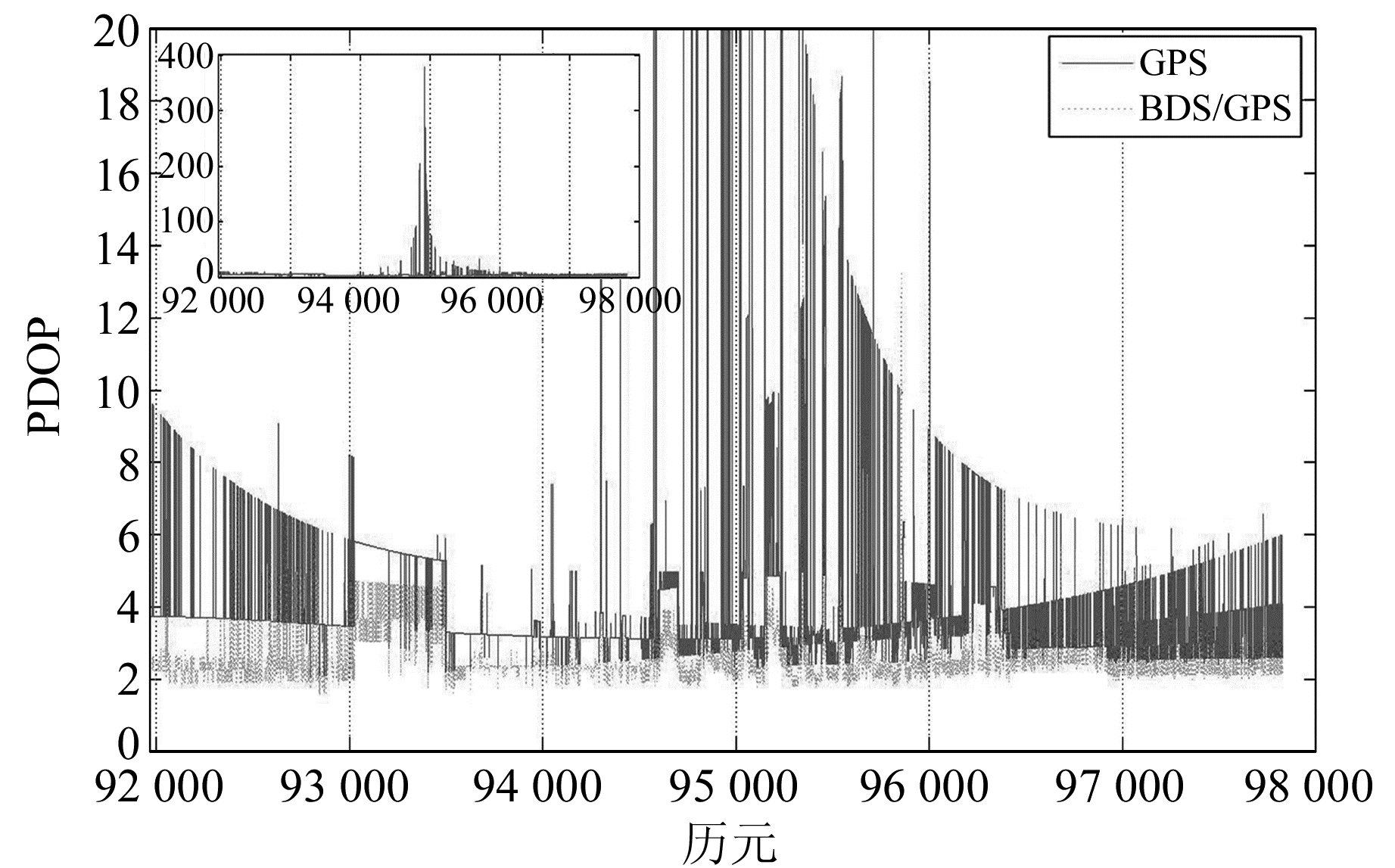
3.2 共视卫星数及PDOP值

图 2给出了在数据采集过程中可接收到的基准站流动站卫星数量，其中BDS共视卫星约7颗，GPS约5颗。可见，BDS/GPS相较于单GPS增加了1倍多的卫星数目，在GPS卫星数目不满足单独定位的相关要求时，BDS的加入会起到关键性作用。图 2中，有个别历元BDS的共视卫星很少，甚至为0，可能是观测环境有高楼遮挡，高度角较高的GEO卫星不可见，导致共视卫星数量迅速减少。图 3给出了GPS和BDS/GPS的PDOP值，可见单GPS的PDOP值的大小变化较频繁，且变化区间大，而BDS/GPS的PDOP值基本稳定在2.0~3.0区间内，没有较大的浮动，说明BDS/GPS相较于单GPS改善了卫星的几何结构。

3.3 载波相位动态差分定位精度

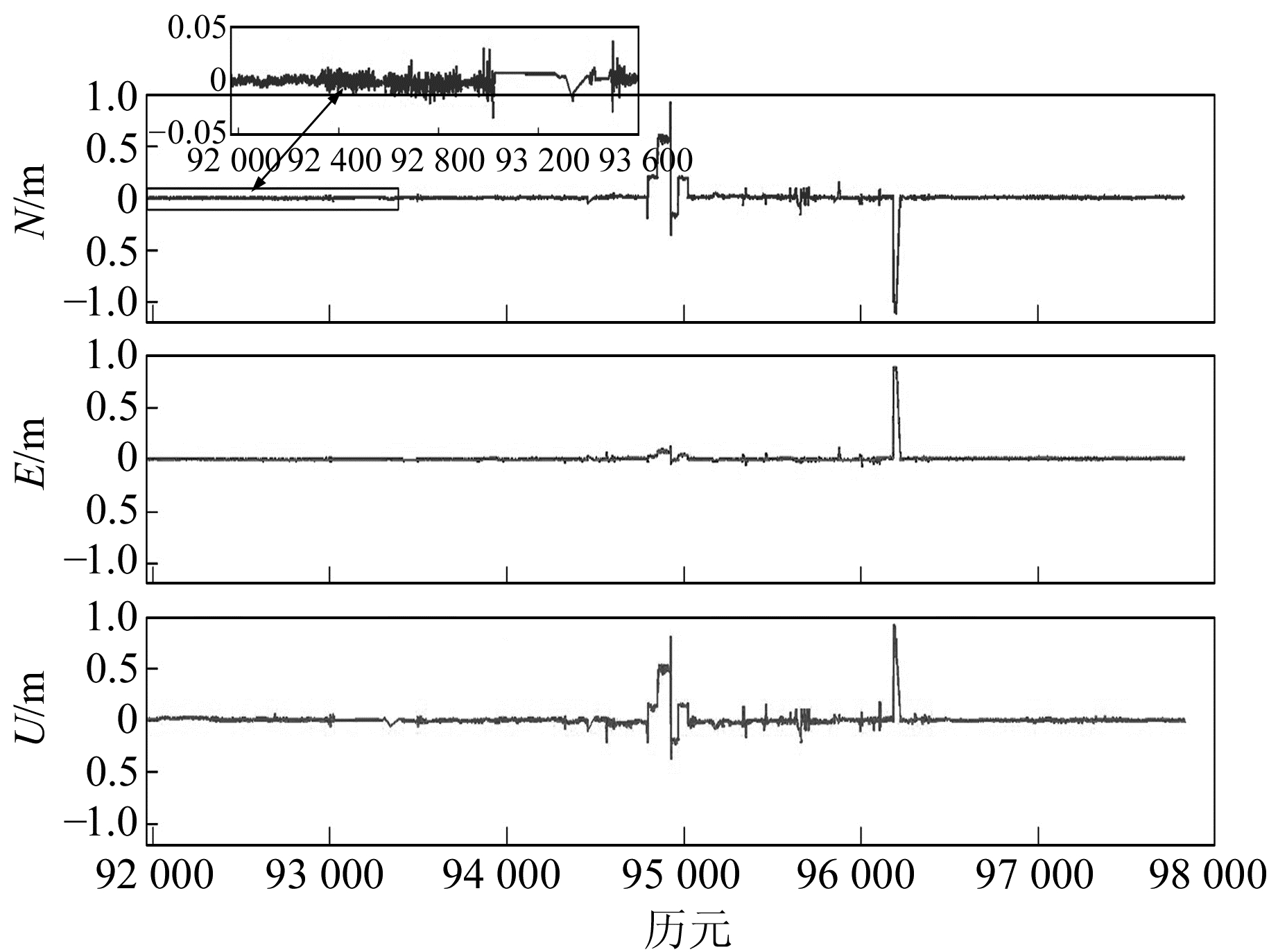
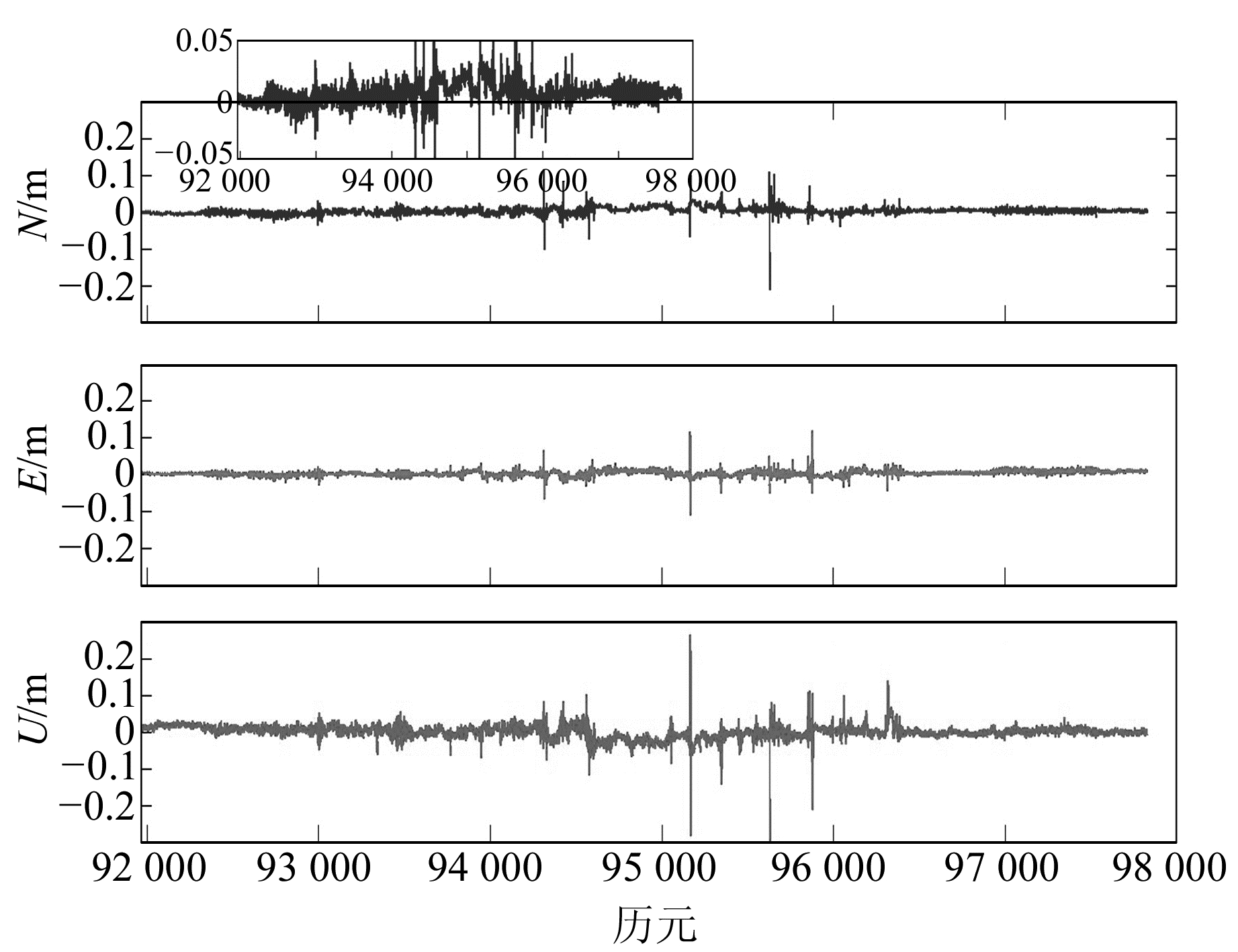
使用自编的GNSS动态差分后处理程序代替IE8.6，仅作GNSS数据处理，并分别与相应的参考值进行比较。GPS以及BDS/GPS动态定位北向(N)、东向(E)、天向(U)的误差序列见图 4和图 5，统计结果见表 2。

由图 4看出，在绝大多数历元GPS单独定位具有较高的精度。以N方向为例，任意截取一段历元区间，如91 965.60~93 000.00 s(局部放大图见图 4)，定位误差小于5 cm。从图 2、图 3看出，这些历元的共视卫星数一般为6，PDOP值一般在2.0~4.0之间，卫星数目足够，几何结构好，故定位精度较好；在93 024.40~93 405.00 s历元区间没有输出定位信息，结合图 2、图 3，此段区间的卫星数保持在5，PDOP值约6.0，由于程序设定PDOP值阈值为5.0，故没有输出定位信息。在94 792.60~95 020.00 s历元区间，模糊度未能正确地固定。由图 2、图 3可知，此段区间的卫星数为4~5颗，而PDOP值变化剧烈，例如94 792.60~94 793.00 s卫星数为4，PDOP值约为83.0，而94 793.20~94 793.80 s卫星数为5，PDOP值约3.60。进一步查看两段区间卫星之间的关系发现，仅有一颗卫星有变动，可见单一系统的卫星结构较易改变，对固定模糊度的影响较大。图 4在96 185.00~96 343.00 s有一处较大的抖动，此段区间卫星数目在3~5间频繁变化，PDOP值在3.5~7.8间变化，且值为7.8左右的居多。可见，在测区环境较复杂的情况下，单系统可接收到的卫星数目有限，且频繁变化，卫星几何结构也普遍较差。

对比图 5和图 4知，BDS/GPS解算结果明显好于GPS单独定位。图 4中没有定位信息的一段历元区间在图 5中可以正常获取信息，且有较高的定位精度，属于§2所述的情况2)；图 5在94 792.60~95 020.00 s模糊度可以固定，但天向坐标离散度比其他历元大，属于情况3)；图 4在96 185.00~96 343.00 s的较大抖动未在图 5出现，属于情况1)和2)。

由表 2看出，无论是平均值、最大值还是标准中误差，BDS/GPS组合均优于GPS单独定位。BDS/GPS水平定位精度优于8 mm，天向为16 mm，而GPS东向仅为3 cm，北向和天向约8 cm；BDS/GPS水平方向平均值为4 mm，天向为0 mm，而GPS在3个方向均约1 cm，故BDS/GPS组合相较GPS定位结果在坐标离散度上有较大改善；GPS的抖动最大，3个方向均约1 m，而BDS/GPS组合均小于0.3 m。

4 结语

在多遮挡环境下，BDS/GPS组合较单GPS有如下优点：

1) 增加了1倍多的共视卫星，改善了卫星的几何结构。

2) 增加了单历元双差模糊度解算的固定率和可靠性。

3) 提高了载波相位动态差分的解算率，即可解算的历元数占总历元数的比例增加。

4) 提高了载波相位动态差分定位的可靠性和精度。