城市环境下GNSS信号会受到严重的遮挡和干扰。随着GNSS技术的不断发展,GPS、GLONASS、BDS、Galileo等多系统融合定位改善了城市环境下的卫星可见情况。以GPS/BDS组合为例,在城市稠密地区进行卫星导航定位,GPS/BDS组合能显著提高定位的有效性和精度[1]。然而常规的GNSS RTK算法在城市环境下特别是动态条件下模糊度固定率很低,cm级定位历元很少,主要是由于部分卫星存在严重的信号干扰,其误差影响了模糊度搜索的固定效率甚至导致模糊度无法固定。
基于此,本文采用部分模糊度固定算法改善城市动态环境下GNSS RTK算法的性能,其出发点在于由于卫星数量较多,固定全部模糊度对GNSS定位并不是必须的,实际定位中可以采取固定一部分模糊度来避免固定失败的发生[2]。国内外许多学者针对部分模糊度固定算法进行了研究,证明部分模糊度固定算法能有效提高GNSS RTK模糊度的固定率和固定效率[3-9]。本文针对城市动态环境的特点,提出基于高度角排序的模糊度分组固定方案,在利用Kalman滤波得到模糊度浮点解之后,对所有模糊度参数进行排序分组,进而分组固定模糊度,优先固定干扰相对较少的高高度角卫星模糊度,进而利用已固定模糊度辅助未固定模糊度整数搜索,最终将固定的模糊度回代入观测方程,得到坐标参数及其他待估参数的固定解。
1 Kalman滤波求解模糊度浮点解RTK算法中首先求解模糊度浮点解,本文使用扩展卡尔曼滤波(extended Kalman filter, EKF)对用户三维坐标、双差模糊度等参数进行估计[10]。
1.1 状态向量除了三维坐标和双差模糊度参数外,对于RTK定位误差中难以通过差分或模型改正的误差项也要作为待估参数进行估计。
RTK算法的主要误差源是双差电离层延迟和对流层延迟。本文对于双差电离层延迟通过双频观测值无电离层组合消除;对于双差对流层延迟,由于双差对流层干延迟模型精度可达mm级[11],而湿延迟难以建立精确模型,将双差对流层干延迟采用模型改正,双差对流层湿延迟作为待估参数与其他参数一起滤波解算。故状态向量如下:
| $ {\mathit{\boldsymbol{X}}_\mathit{k}}{\rm{ = (d}}\mathit{X}{\rm{, d}}\mathit{Y}{\rm{, d}}\mathit{Z}{\rm{, \Delta }}{{\mathit{T}}_{\mathit{z}{\rm{, }}\mathit{br}}}{\rm{, \Delta }}\nabla \mathit{N}{\rm{)}} $ | (1) |
式中,dX、dY、dZ为流动站坐标改正数,N为载波相位的整周模糊度,ΔTz, br为对流层湿延迟。
双差对流层湿延迟可表示为天顶对流层湿延迟和投影函数:
| $ \begin{array}{l} {\rm{\Delta }}\nabla \mathit{T}_{\mathit{br}}^{\mathit{ij}}{\rm{ = }}\left[{\mathit{f}\left( {\mathit{E}_r^\mathit{j}} \right){\mathit{T}_{\mathit{z}{\rm{, }}\mathit{r}}}{\rm{-}}\mathit{f}\left( {\mathit{E}_\mathit{b}^\mathit{j}} \right){\mathit{T}_{\mathit{b}{\rm{, }}\mathit{r}}}} \right]{\rm{ - }}\\ \;\;\;\;\;\;\;\;\;\;{\rm{[}}\mathit{f}{\rm{(}}\mathit{E}_\mathit{r}^\mathit{i}{\rm{)}}{\mathit{T}_{\mathit{z}{\rm{, }}\mathit{r}}}{\rm{-}}\mathit{f}{\rm{(}}\mathit{E}_\mathit{b}^\mathit{i}{\rm{)}}{\mathit{T}_{\mathit{z}{\rm{, }}\mathit{b}}}{\rm{]}} \end{array} $ | (2) |
式中,Δ∇表示双差组合符,下标表示接收机编号(b为基准站,r为流动站),上标表示卫星号(i为参考星,j为其他卫星);f为对流层湿延迟投影函数,本文采用NMF模型,f为高度角的函数;E为高度角;Tz为天顶对流层湿延迟。
由于Ebi
| $ {\rm{\Delta }}\nabla \mathit{T}_{\mathit{br}}^{\mathit{ij}}{\rm{ = [}}\mathit{f}{\rm{(}}{\mathit{\theta }^\mathit{j}}{\rm{)-}}\mathit{f}{\rm{(}}{\mathit{\theta }^\mathit{i}}{\rm{)][}}{\mathit{T}_{\mathit{z}{\rm{, }}\mathit{r}}}{\rm{-}}{\mathit{T}_{\mathit{z}{\rm{, }}\mathit{b}}}{\rm{]}} $ | (3) |
状态方程需要表示出状态向量的微分方程,其中坐标通过三差模型求解出基线变化量,再除以时间作为三维坐标参数的微分。双差天顶对流层湿延迟采用一阶高斯-马尔科夫模型估计[12],故状态方程微分形式如下:
| $ \left[\begin{array}{l} \;{\rm{d}}\mathit{\dot X}\\ {\rm{\Delta }}\nabla \mathit{\dot T} \end{array} \right]{\rm{ = }}\left[\begin{array}{l} \;\;\;\;{\rm{TDX/d}}\mathit{t}\\ {\rm{-1/}}\mathit{\tau }{\rm{\cdot\Delta }}\nabla \mathit{T}{\rm{ }} \end{array} \right]{\rm{ + }}\left[\begin{array}{l} {\mathit{W}_{{\rm{TDX}}}}\\ \;\;\mathit{w} \end{array} \right]{\rm{}} $ | (4) |
式中,TDX为三差解算的三维坐标变化量,dt表示历元间隔,WTDX为三差解算的噪声,τ为一阶高斯-马尔科夫过程的相关时间,w表示驱动白噪声。
1.3 观测方程数学模型通过站间星际双差观测方程表示为:
| $ \begin{array}{l} \mathit{\lambda }{\rm{\Delta }}\nabla \mathit{\varphi }_{\mathit{br}}^{\mathit{ij}}{\rm{ = \Delta }}\nabla \mathit{\rho }_{\mathit{br}}^{\mathit{ij}{\rm{0}}}{\rm{ + }}\nabla {\mathit{l}^{\mathit{ij}}}{\rm{d}}\mathit{X}{\rm{ + }}\nabla {\mathit{m}^{\mathit{ij}}}{\rm{d}}\mathit{Y}{\rm{ + }}\\ \;\;\;\;\;\;\;\;\;\;\nabla {\mathit{n}^{\mathit{ij}}}{\rm{d}}\mathit{Z}{\rm{ - }}\mathit{\lambda }{\rm{\Delta }}\nabla \mathit{N}_{\mathit{br}}^{\mathit{ij}}{\rm{ + \Delta }}\nabla \mathit{T}_{\mathit{br}}^{\mathit{ij}} \end{array} $ | (5) |
式中,λ表示载波波长,ρ0为接收机到卫星之间的近似几何距离,l、m、n基站到卫星的方向余弦,dX、dY、dZ为流动站坐标改正数,N为载波相位的整周模糊度。对于GPS/BDS双系统而言,组双差方式有两种:一种是采用GPS和BDS各系统选择自己的参考星分开组双差;另一种是仅选择一个参考星,组混合双差[13]。考虑到组混合双差需要引入系统间偏差,算法较为复杂,本文采用第一种方案。
随机模型采用基于高度角定权的方案,根据经验,GPS和BDS相对权比关系为1.5:1。
2 部分模糊度固定算法采用基于高度角分组的部分模糊度固定的算法,其基本原理是在求解得到模糊度浮点解之后,对所有模糊度参数按照高度角进行排序分组,优先固定高度角较高组的卫星,进而利用已固定模糊度辅助未固定模糊度整数搜索,最终将固定的模糊度回代入观测方程,得到坐标参数及其他待估参数的固定解[14]。其算法流程如图 1所示。
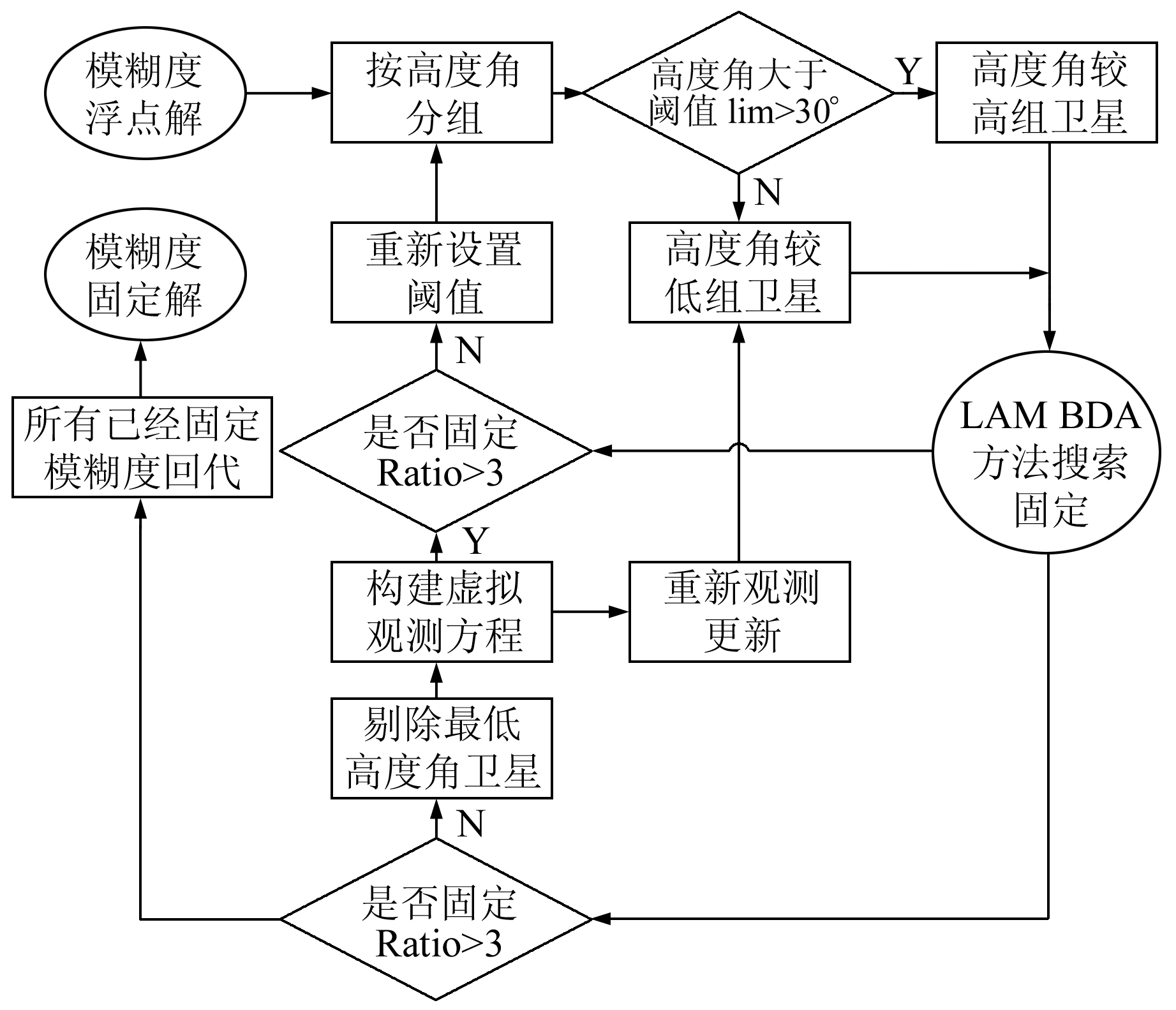
|
图 1 部分模糊度固定算法流程 Fig. 1 Flow chart of partial ambiguity algorithm |
为了评估部分模糊度固定算法在城市动态环境下的性能,在武汉市设计了车载实验,设计路线包括林荫道、高楼峡谷、高架桥等。
为了对比RTK结果的绝对精度,测试中搭载了武汉迈普时空导航科技有限公司的战术级GNSS/INS组合导航系统POS310,其GNSS板卡采用Trimble BD982,IMU采用高精度光纤陀螺(零偏0.5°/h),挠性石英加速度计(零偏50 mGal)。由于城市环境下GNSS RTK/INS紧组合可以大大提高系统的可靠性,并提供更连续的高精度导航定位结果[15],所以可将GNSS RTK/INS紧组合结果作为参考真值,采用迈普时空开发的GINS软件提供RTK/INS紧组合平滑结果。
本次实验主要分析验证以下3个方面的内容。首先,验证在城市动态环境下GPS/BDS双系统RTK算法可用卫星数是否足以支持部分固定算法;再者,根据实际卫星观测情况选择合适的分组高度角阈值,以PDOP(位置精度衰减因子)作为依据对比分组前后卫星观测几何图形的强度;最后,验证部分模糊度固定算法的可用性,对比部分模糊度固定算法与常规算法定位结果的精度。
设置截止卫星高度角为15°,卫星观测情况如图 2所示。
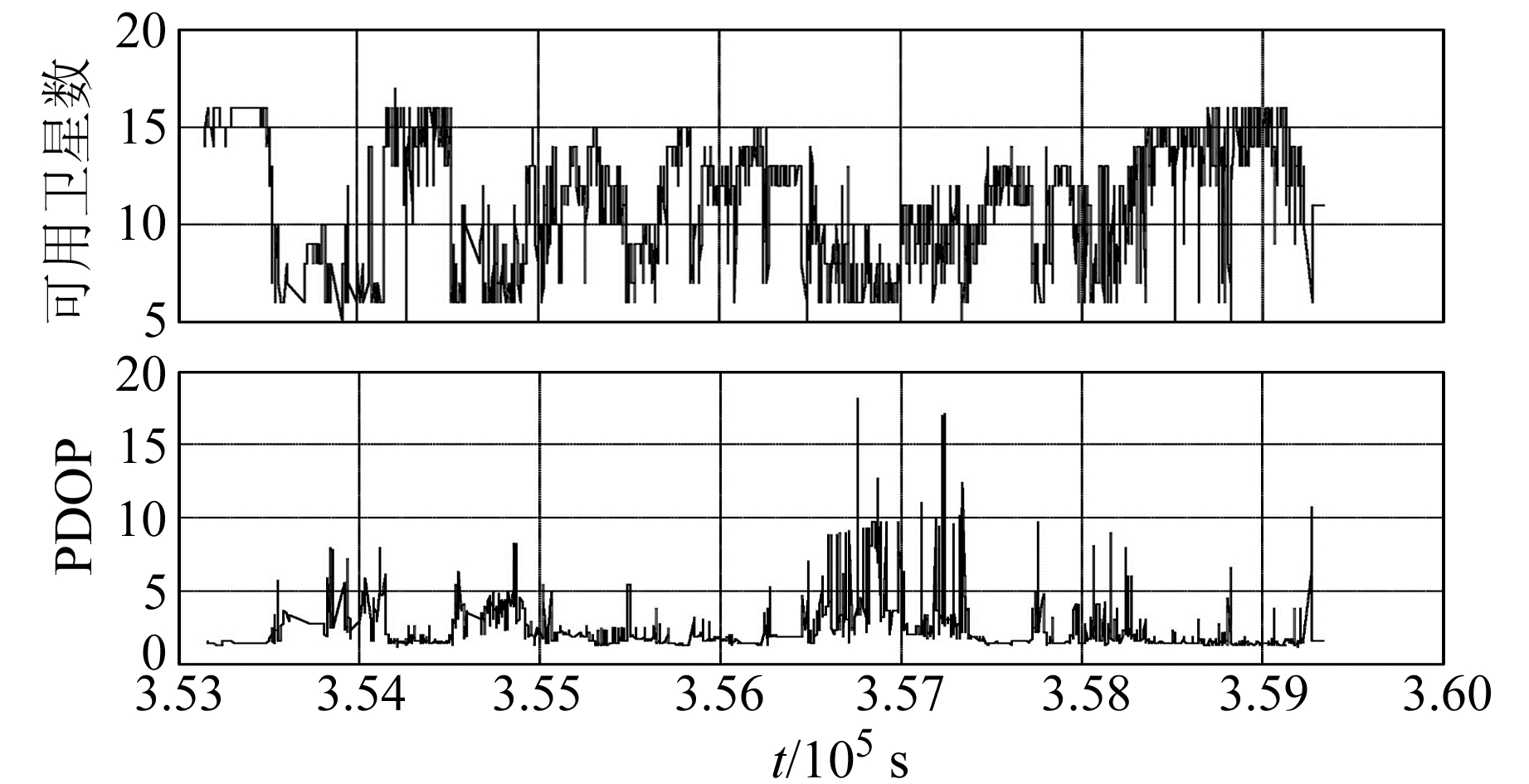
|
图 2 GPS/BDS可用卫星数及PDOP值 Fig. 2 GPS/BDS satellite number and PDOP value |
根据卫星观测情况,设置高度角阈值为30°。分组后,高度角大于阈值的卫星观测情况如图 3所示。

|
图 3 GPS/BDS可用卫星数及PDOP值 Fig. 3 GPS/BDS satellite number and PDOP value |
由图可知,城市动态环境下GPS/BDS双系统多数观测历元可见卫星在7~15颗,而大于30°分组阈值的卫星数在6~10颗,能够支持部分模糊度固定算法;PDOP值在分组前多数观测历元小于5,而大于阈值的卫星PDOP值有所增加,但多数历元仍然小于10,显然卫星几何图形强度有所下降,不过仍在可用范围内。
为了验证部分模糊度固定算法的可用性和精度,从模糊度固定情况和定位三维坐标精度两个方面进行分析。
模糊度固定率是判断RTK算法结果优劣的重要指标。本文模糊度是否固定的判断采用广泛应用的Ratio检验。设置Ratio阈值为3,大于3则认为固定,否则则认为是浮点解。常规RTK算法结果Ratio值及模糊度固定情况如图 4所示。
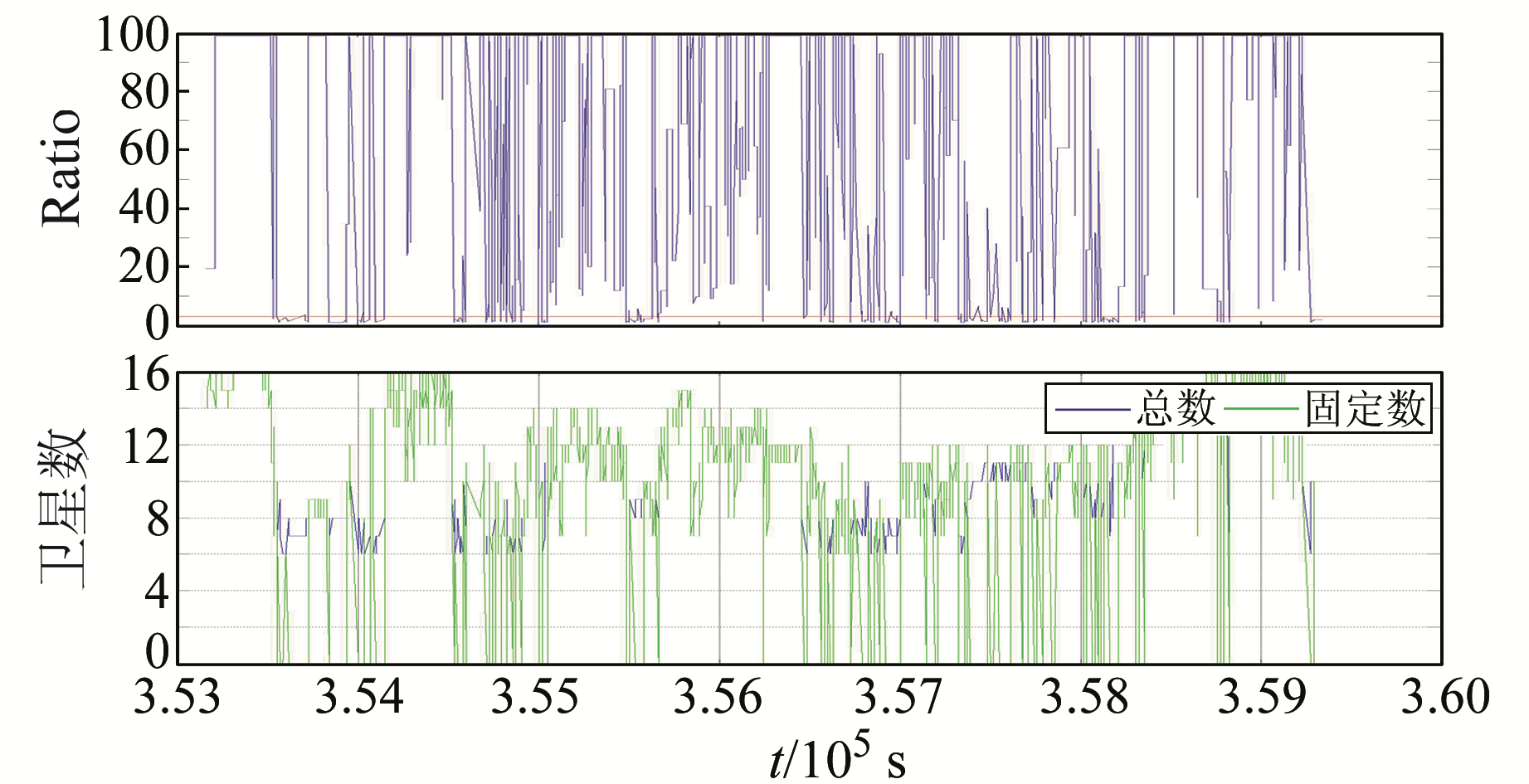
|
图 4 GPS/BDS RTK模糊度解算质量 Fig. 4 GPS/BDS ambiguity solution quality in conventional RTK algorithm |
本文采用的基于部分模糊度固定的RTK算法解算结果Ratio值及模糊度固定情况如图 5所示。
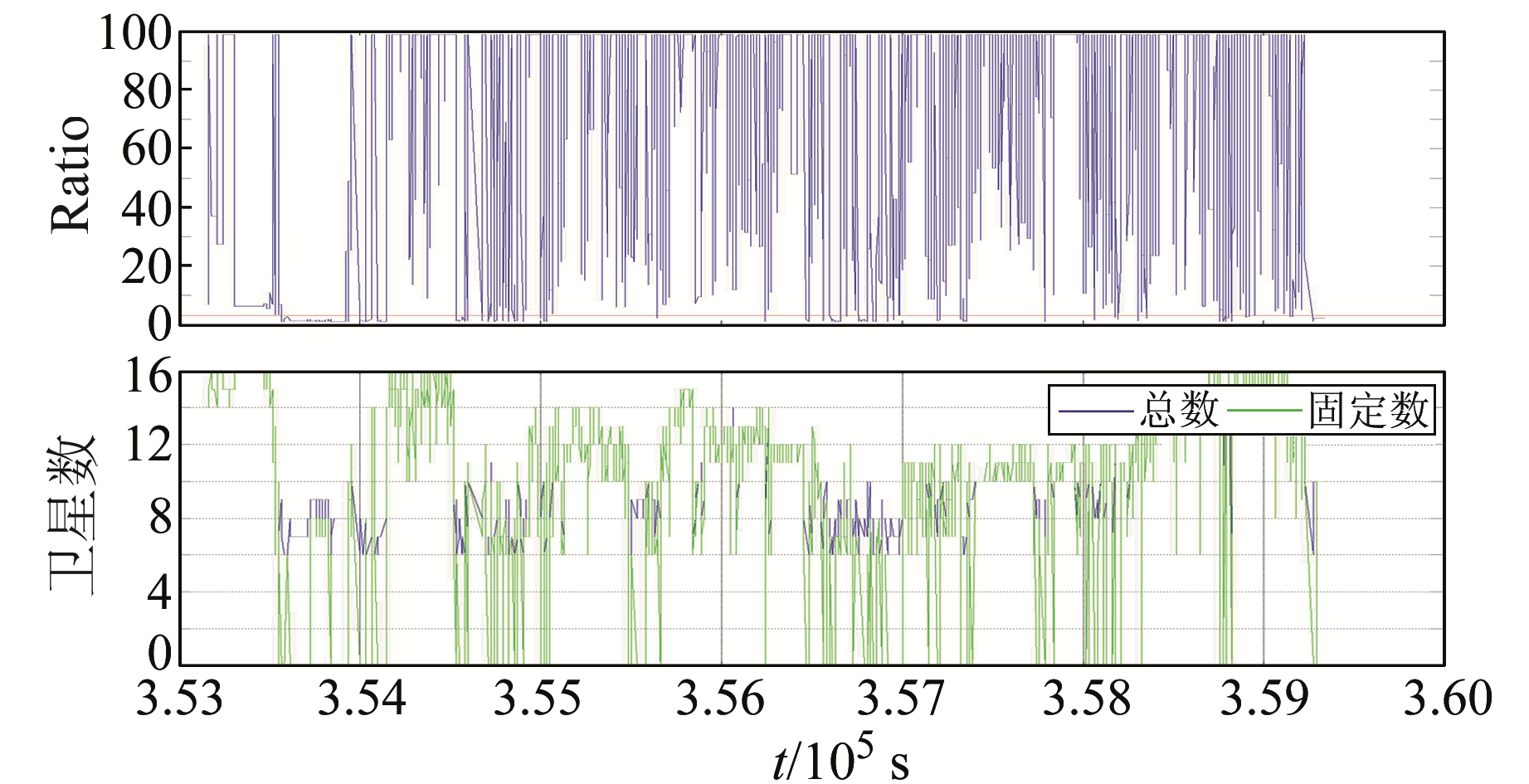
|
图 5 GPS/BDS RTK部分模糊度固定算法解算质量 Fig. 5 GPS/BDS ambiguity solution quality in partial ambiguity fixing algorithm |
为更加清晰地反映两种算法的模糊度固定情况,分别统计两种算法的模糊度固定率,如表 1所示。从表 1可以看出,城市动态环境下,GPS/BDS双系统大部分情况下可达到定位要求,但是模糊度固定历元相对较少;基于部分模糊度固定的RTK算法的模糊度固定率比常规RTK算法提高10%以上。
|
|
表 1 模糊度固定情况对比 Tab. 1 Comparison of ambiguity fixing result |
模糊度固定率的提高一定程度上证明了城市动态环境下部分模糊度固定算法的可用性,但是直接反映定位结果质量的是三维坐标精度。本文以RTK/INS紧组合的结果作为参考真值,对比了部分模糊度固定算法和常规RTK算法的定位质量。
两种算法定位结果的位置精度分别如图 6、图 7所示,其中位置误差都已经转换到参考真值的站心坐标系下。可以看出,两种算法的定位结果误差服从零均值分布,大部分误差都在cm级或dm级;基于部分模糊度固定的RTK算法相对常规RTK算法而言,位置误差更小。另外,两种算法都存在误差较大的点是由于模糊度浮点解或模糊度固定错误造成。
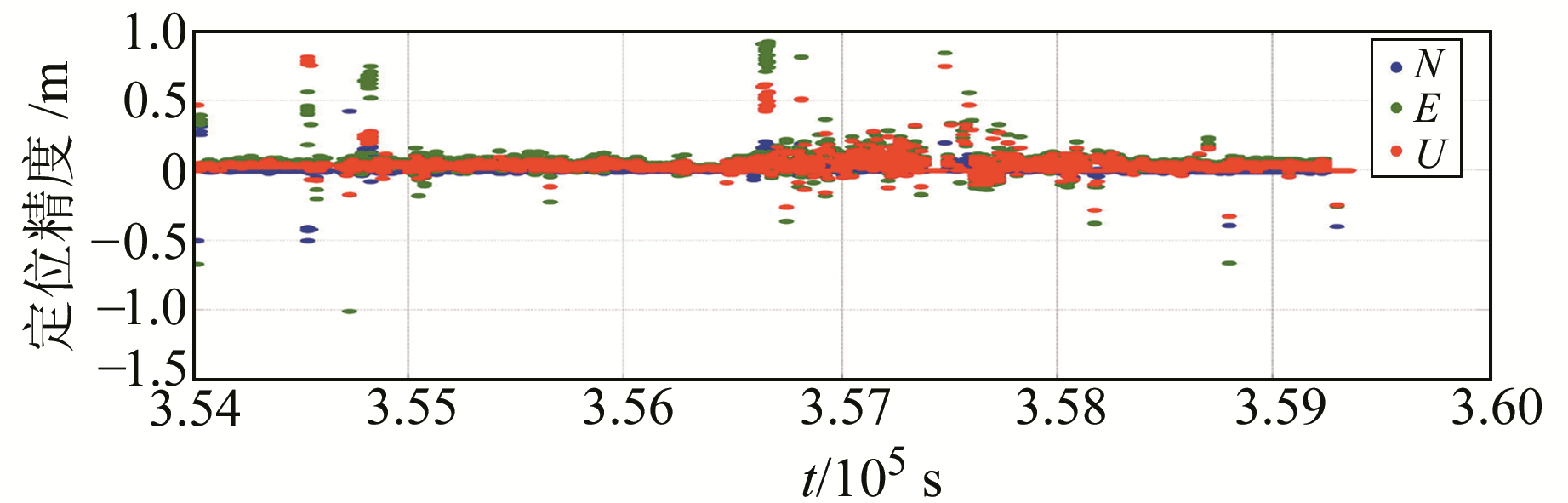
|
图 6 GPS/BDS RTK定位精度 Fig. 6 Coordinate precision of ambiguity fixed solution in conventional RTK algorithm |

|
图 7 GPS/BDS部分模糊度固定算法定位精度 Fig. 7 Coordinate precision of ambiguity fixed solution in partial ambiguity fixing algorithm |
为了更加清晰地反映两种算法定位结果的位置精度,分别统计了两种方案的可定位历元位置误差和模糊度固定历元位置误差(表 2,单位m)。
|
|
表 2 位置误差对比 Tab. 2 Comparison of positioning error |
可以看出,所有可定位历元的位置误差统计结果中,两种算法的位置统计误差都在dm级,这是由于浮点解精度较低造成的;垂向误差显著大于平面,这是由于大气误差残差影响都体现在高程方向;部分模糊度固定算法统计精度优于常规算法,这是由于部分模糊度固定算法的模糊度固定率更高。
另一方面,模糊度固定历元位置误差统计结果中,两种算法的位置统计误差都在cm级;部分模糊度固定算法的误差统计结果略大于常规RTK算法,这是由于部分模糊度固定算法在仅固定高高度角卫星时,卫星几何分布较差,相应的PDOP值较大造成的。
4 结语本文研究了基于高度角分组的部分模糊度固定算法,并将其应用于城市动态环境。通过实际车载测试分析,城市动态环境下GPS/BDS双系统可见卫星数大部分情况下大于7颗,可以满足部分模糊度固定算法的需求;城市动态环境下,部分模糊度固定算法可以显著提高模糊度的固定率,从而提高RTK算法的位置精度。
| [1] |
尹潇, 胡丛纬, 姚连璧, 等. 一种基于GPS/BDS观测值的抗多路径误差导航定位算法[J]. 大地测量与地球动力学, 2017(5): 457-461 (Yin Xiao, Hu Congwei, Yao Lianbi, et al. A Multipath Reduction Algorithm Based on GPS/BDS Measurements[J]. Journal of Geodesy and Geodynamics, 2017(5): 457-461)
(  0) 0) |
| [2] |
赵兴旺, 张翠英. 精密单点定位部分模糊度固定方法[J]. 中国空间科学技术, 2013, 2(1): 37-43 (Zhao Xingwang, Zhang Cuiying. Partial Ambiguity Fixing Method and Analysis for Precise Point Positioning[J]. Chinese Space Science and Technology, 2013, 2(1): 37-43 DOI:10.3780/j.issn.1000-758X.2013.01.006)
(  0) 0) |
| [3] |
阳仁贵, 欧吉坤, 袁运斌. 部分搜索法提高GPS相位模糊度解算的效率和成功率[J]. 武汉大学学报:信息科学版, 2007, 32(2): 160-163 (Yang Rengui, Ou Jikun, Yuan Yunbin. Facilitating Efficiency and Success Rate of Resolving GPS Phase Ambiguity with Parts Search Method[J]. Geomatics and Information Science of Wuhan University, 2007, 32(2): 160-163)
(  0) 0) |
| [4] |
Verhagen A A, Teunissen P J G, Van der Marel H, et al. GNSS Ambiguity Resolution: Which Subset to Fix?[C]. IGNSS Symposium 2011, International Global Navigation Satellite Systems Society, University of New South Wales, Sydney, 2011
(  0) 0) |
| [5] |
Li B, Shen Y, Feng Y, et al. GNSS Ambiguity Resolution with Controllable Failure Rate for Long Baseline Network RTK[J]. Journal of Geodesy, 2014, 88(2): 99-112 DOI:10.1007/s00190-013-0670-z
(  0) 0) |
| [6] |
Li B, Teunissen P J G. GNSS Antenna Array-Aided CORS Ambiguity Resolution[J]. Journal of Geodesy, 2014, 88(4): 363-376 DOI:10.1007/s00190-013-0688-2
(  0) 0) |
| [7] |
Andreas B. On Reliable Data-Driven Partial GNSS Ambiguity Resolution[J]. GPS Solutions, 2015, 19(3): 411-422 DOI:10.1007/s10291-014-0401-9
(  0) 0) |
| [8] |
Dennis O, Arora B S, Teunissen P J G. Predicting the Success Rate of Long-Baseline GPS+ Galileo (Partial) Ambiguity Resolution[J]. Journal of Navigation, 2014, 67(3): 385-401 DOI:10.1017/S037346331400006X
(  0) 0) |
| [9] |
高旺, 高成发, 潘树国, 等. 基于部分固定策略的多系统长距离基准站间模糊度快速解算[J]. 武汉大学学报:信息科学版, 2017, 42(4): 558-562 (Gao Wang, Gao Chengfa, Pan Shuguo, et al. Fast Ambiguity Resolution between GPS/GLONASS/BDS Combined Long-Range Base Stations Based on Partial-Fixing Strategy[J]. Geomatics and Information Science of Wuhan University, 2017, 42(4): 558-562)
(  0) 0) |
| [10] |
王虎, 王解先, 白贵霞, 等. RTK定位模型研究与精度分析[J]. 大地测量与地球动力学, 2010, 30(4): 113-116 (Wang Hu, Wang Jiexian, Bai Guixia, et al. Research and Accuracy Analysis on Real Time Kinematic Positioning Model[J]. Journal of Geodesy and Geodynamics, 2010, 30(4): 113-116)
(  0) 0) |
| [11] |
Xie L, Zhu G X, Wang Y Q, et al. Real Time Vehicles Tracking Based on Kalman Filter in a Video-Based ITS[C]. IEEE Conf on Communications, Circuits and System, Hong Kong, 2005
(  0) 0) |
| [12] |
徐彦田, 程鹏飞, 蔡艳辉. 中长基线单基准站动态定位卡尔曼滤波算法[J]. 西南交通大学学报, 2013, 48(2): 317-322 (Xu Yantian, Cheng Pengfei, Cai Yanhui. Kalman Filter Algorithm for Medium-Range Real-Time Kinematic Positioning with One Reference Station[J]. Journal of Southwest Jiaotong University, 2013, 48(2): 317-322)
(  0) 0) |
| [13] |
楼益栋, 龚晓鹏, 辜声峰, 等. GPS/BDS混合双差分RTK定位方法及结果分析[J]. 大地测量与地球动力学, 2016, 36(1): 1-5 (Lou Yidong, Gong Xiaopeng, Gu Shengfeng, et al. An Algorithm and Results Analysis for GPS+BDS Inner System Mix Double-Difference RTK[J]. Journal of Geodesy and Geodynamics, 2016, 36(1): 1-5)
(  0) 0) |
| [14] |
Hu N N, Zhang H P, Li T. Research on Fast RTK GNSS Algorithm Based on Partial Ambiguity Resolution[C]. China Satellite Navigation Conference, CSNC 2017
(  0) 0) |
| [15] |
李团, 章红平, 牛小骥, 等. 城市环境下BDS/GPS RTK/INS紧组合算法性能分析[J]. 测绘通报, 2016(9): 9-12 (Li Tuan, Zhang Hongping, Niu Xiaoji, et al. Performance Analysis of BDS+GPS RTK+INS Tightly Coupled Algorithm in Urban Environments[J]. Bulletin of Surveying and Mapping, 2016(9): 9-12)
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38

