2. 西安测绘总站,西安市西影路36号,710054
似大地水准面是我国高程系统的起算基准面,其格网数值模型可作为测定正常高的参考框架,是地球物理科学研究中一项非常重要的工作[1]。受重力场模型阶次限制,目前最高为2 190阶次的EGM2008模型仅能反映地表 5′×5′分辨率的似大地水准面信息,需要通过剩余地形模型进行相关改正[2-3]。通常采用高精度SRTM数字地形模型[4]和DTM2006.0超高阶地球DTM模型[5]构建剩余地形模型。文献[6]针对EGM2008模型构建过程中存在的不足,提出用GOCE重力场模型替换EGM2008模型的中低频部分,用剩余地形模型(RTM)拓展EGM2008模型的甚高频信号。实测GPS/水准数据表明,GOCE模型对高程异常的贡献达到43%,而RTM贡献为1 cm。文献[7]将EGM2008模型高程异常和RTM高程异常从GPS/水准点上的实测高程异常中扣除,对残余值进行拟合,从而进一步提高GPS高程转换的精度。文献[8]以构建RTM高程异常的数字地形模型的分辨率及其参考面的选择为研究对象,系统分析了两者对RTM高程异常计算效率及精度的影响。
本文采用上述模型精化似大地水准面,比较不同积分半径组合后得到的RTM高程异常精度和计算效率,采用CGGM2015模型验证水准面结果的可靠性,并利用GPS/水准点数据进行检核。
1 基本原理 1.1 长波高程异常计算点P上的重力场球谐系数高程异常为[9]:
| $ \begin{array}{l} \;\;\;{\zeta _p}\left( {\varphi, \lambda, \rho } \right) = \frac{{fM}}{{\rho \gamma }}\sum\limits_{n = 2}^N {{{\left( {\frac{a}{\rho }} \right)}^n}} \\ \sum\limits_{m = 0}^n {\left( {\bar C_{nm}^*\cos m\lambda + {{\bar S}_{nm}}\sin m\lambda } \right){{\bar P}_{nm}}\left( {\cos \theta } \right)} \end{array} $ | (1) |
式中,(θ, λ, ρ)为以地心为坐标原点的计算点球坐标,f为引力常数,M为地球质量,a为参考椭球的长半径,γ为计算点的正常重力值,Pnm(cosθ)为完全正常化的勒让德函数,Cnm*和Snm为完全规格化位系数。
1.2 剩余地形模型的计算采用DTM2006.0模型,地面任意一点P的模型高程为[10]:
| $ \begin{array}{l} {H^{{\rm{DTM2006}}{\rm{.0}}}} = \sum\limits_{n = 0}^{n{_{\max }}} {\sum\limits_{m = 0}^n {\left( {{H_{{{\bar C}_{nm}}}}\cos \left( {m\lambda } \right)} \right.} } + \\ \;\;\;\;\;\left. {{H_{{{\bar S}_{nm}}}}\sin \left( {m\lambda } \right)} \right){{\bar P}_{nm}}\left( {\cos \theta } \right) \end{array} $ | (2) |
式中,HCnm、HSnm为正常化的球谐地形高系数。SRTM模型囊括了包括欧亚、北美、南美、非洲、澳洲与其他岛屿等6个资料库,陆地覆盖范围为60°N~57°S。DTM2006.0为2 190阶次的地球DTM模型,能够反映5′×5′的地形信息,用于SRTM地形模型中的中、长波部分的移去:
| $ {H^{{\rm{RTM}}}} = {H^{{\rm{SRTM}}}}-{H^{{\rm{DTM2006}}{\rm{.0}}}} $ | (3) |
式中,RTM数据能够反映出高于5′×5′分辨率的高频地形信息。
1.3 高程异常模型构建采用六棱柱积分法计算RTM高程异常,每个棱柱体对应的引力位为:
| $ V = G\rho \int\limits_{{x_1}}^{{x_2}} {\int\limits_{{y_1}}^{{y_2}} {\int\limits_{{z_1}}^{{z_2}} {\frac{{{\rm{d}}x{\rm{d}}y{\rm{d}}z}}{r}} } } $ | (4) |
式中,
| $ \begin{array}{l} \;\;\;\;V = G{\rho _0}|||xy\ln \left( {z + r} \right) + yz\ln \left( {x + r} \right) + \\ zx\ln \left( {y + r} \right)-\frac{{{x^2}}}{2}{\tan ^{-1}}\left( {\frac{{yz}}{{xr}}} \right)-\frac{{{y^2}}}{2}{\tan ^{ - 1}}\left( {\frac{{xz}}{{yr}}} \right) - \\ \;\;\;\;\;\;\;\;\frac{{{z^2}}}{2}{\tan ^{ - 1}}\left( {\frac{{xy}}{{zr}}} \right)\left| {_{{x_{ij, 1}}}^{{x_{ij, 2}}}} \right.\left| {_{{y_{ij, 1}}}^{{y_{ij, 2}}}} \right.\left| {_{{z_{ij, 1}}}^{{z_{ij, 2}}}} \right. \end{array} $ | (5) |
式中,
| $ {\zeta ^{{\rm{prism}}}} = \frac{V}{{{\gamma _{\rm{Q}}}}} $ | (6) |
计算点P的RTM高程异常为计算区域内所有单个棱柱对应的高程异常之和:
| $ {\zeta ^{{\rm{RTM}}}} = \sum\limits_{i = 1}^k {{\zeta ^{{\rm{prism}}}}\left( i \right)} $ | (7) |
利用式(2)可获得任意点的重力场模型高程异常ζEGM2008,由式(5)、(6)、(7)可获得剩余地形模型高程异常ζRTM,任意点P的高程异常由3个部分构成:
| $ \zeta = {\zeta ^{{\rm{RTM}}}} + {\zeta ^{{\rm{EGM2008}}}} + {\zeta ^{{\rm{RES}}}} $ | (8) |
式中,ζRES为残余高程异常。
利用RTM精化大地水准面流程如下:
1) 计算测区中GPS/水准控制点实测高程异常ζ;
2) 计算重力场EGM2008地球重力场模型高程异常ζEGM2008;
3) 基于SRTM和DTM2006.0计算RTM高程异常ζRTM;
4) 计算GPS/水准控制点上的残余高程异常ζRES,将其格网化后得到残余高程异常模型。
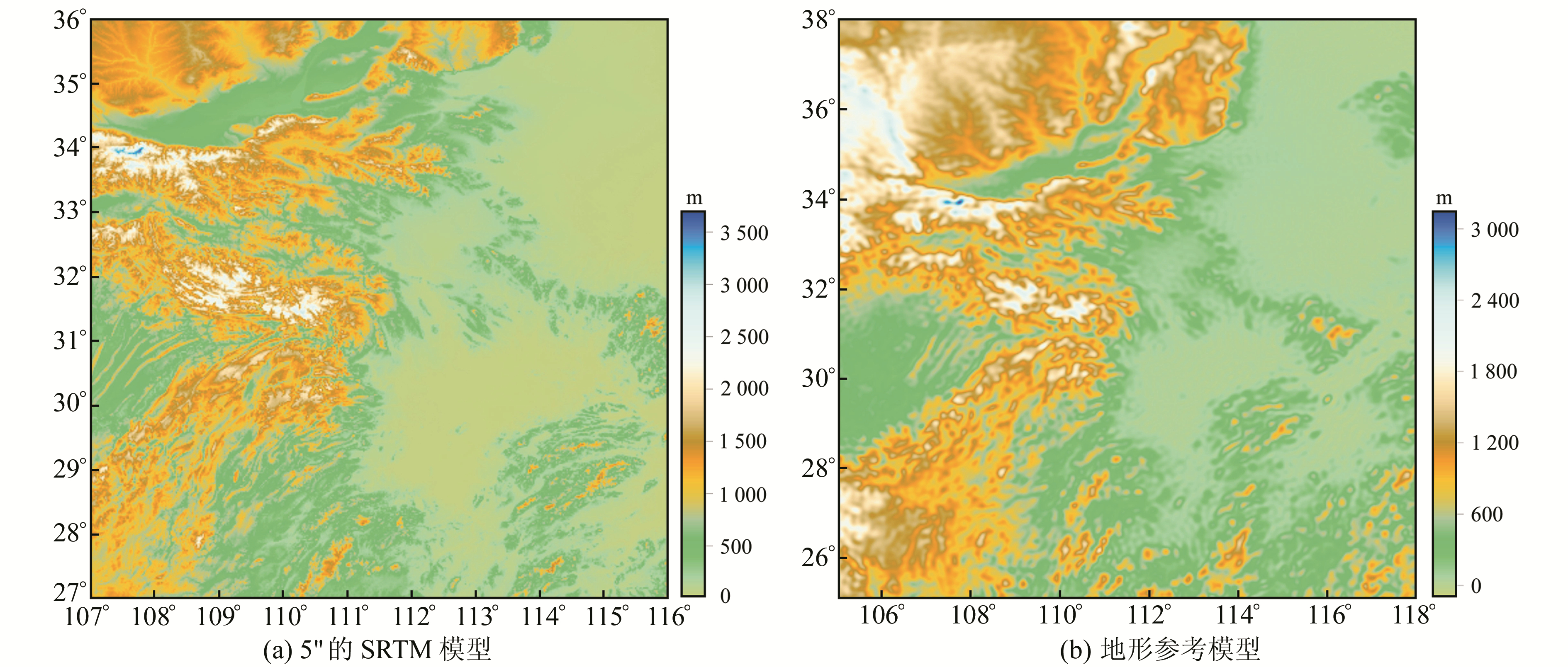
2 实验与分析 2.1 数据准备选择我国中部地区(27°~36°N,107°~116°E)作为实验对象,收集以下几组数据:1)分辨率为3″和15″的SRTM高精度地形数据,如图 1(a)所示;2)采用2 190阶的DTM2006.0地形模型得到分辨率为15″的地形参考面模型,如图 1(b)所示;3)区域内高精度GPS/水准控制点共430个,检核点97个;4)西安测绘总站发布的CGGM2015高程异常模型。
|
图 1 数字地形模型 Fig. 1 DTM |
计算RTM高程异常时,积分半径越大,计算点P的RTM高程异常越精确,但计算量也随之增大[5]。采用细密/粗糙格网积分法,在计算点内圈R1的半径区域采用3″分辨率的SRTM数据,外圈R1~R2的半径区域采用15″分辨率的SRTM数据;地形参考面模型采用15″分辨率的DTM2006.0模型生成。为确定合适的内圈半径,将外圈半径固定为R2=200 km,内圈从R1=25 km开始,以25 km的间隔距离逐渐扩展,随着内圈半径的扩大,RTM高程异常值差异变小,当差异小于一定量级时即为合适的内圈半径。表 1给出了5种不同的积分半径组合方案。
|
|
表 1 不同积分半径组合方案 Tab. 1 Different integral radius combination scheme |
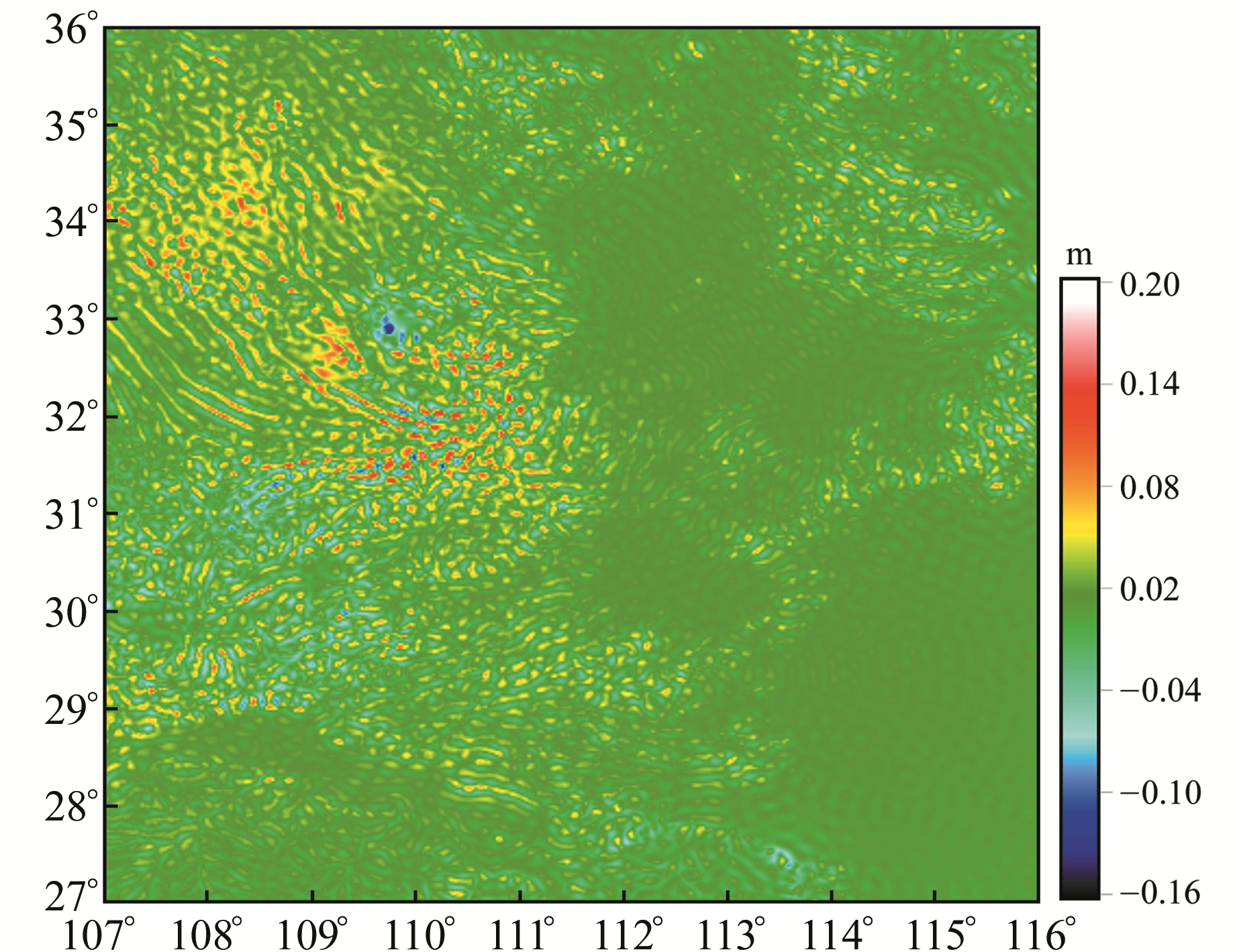
以1′为间隔计算540×540个网格点的RTM高程异常,图 2给出了采用方案C计算的RTM高程异常。考虑到方案E积分的格网数量较多,高程异常模型精度最高,将其作为参考验证方案A~D的精度及计算效率,图 3和表 2给出了方案A~D与方案E的结果之差。可以看出,随着计算半径的扩大,模型精度不断提升,而计算效率不断下降,其效率相比方案E分别提升55.8%、46.5%、38.0%、23.1%。当计算半径增至75 km后,RTM高程异常精度和差值最大值控制在1 mm以内,结果趋于稳定。同时顾及模型精度和计算效率,选用方案C为宜。
|
图 2 RTM高程异常 Fig. 2 Height anomaly of RTM |

|
图 3 RTM高程异常比较结果 Fig. 3 Comparison of the results of RTM height anomaly |
|
|
表 2 不同积分半径组合方案结果比较 Tab. 2 Comparison of the results of different combination schemes |
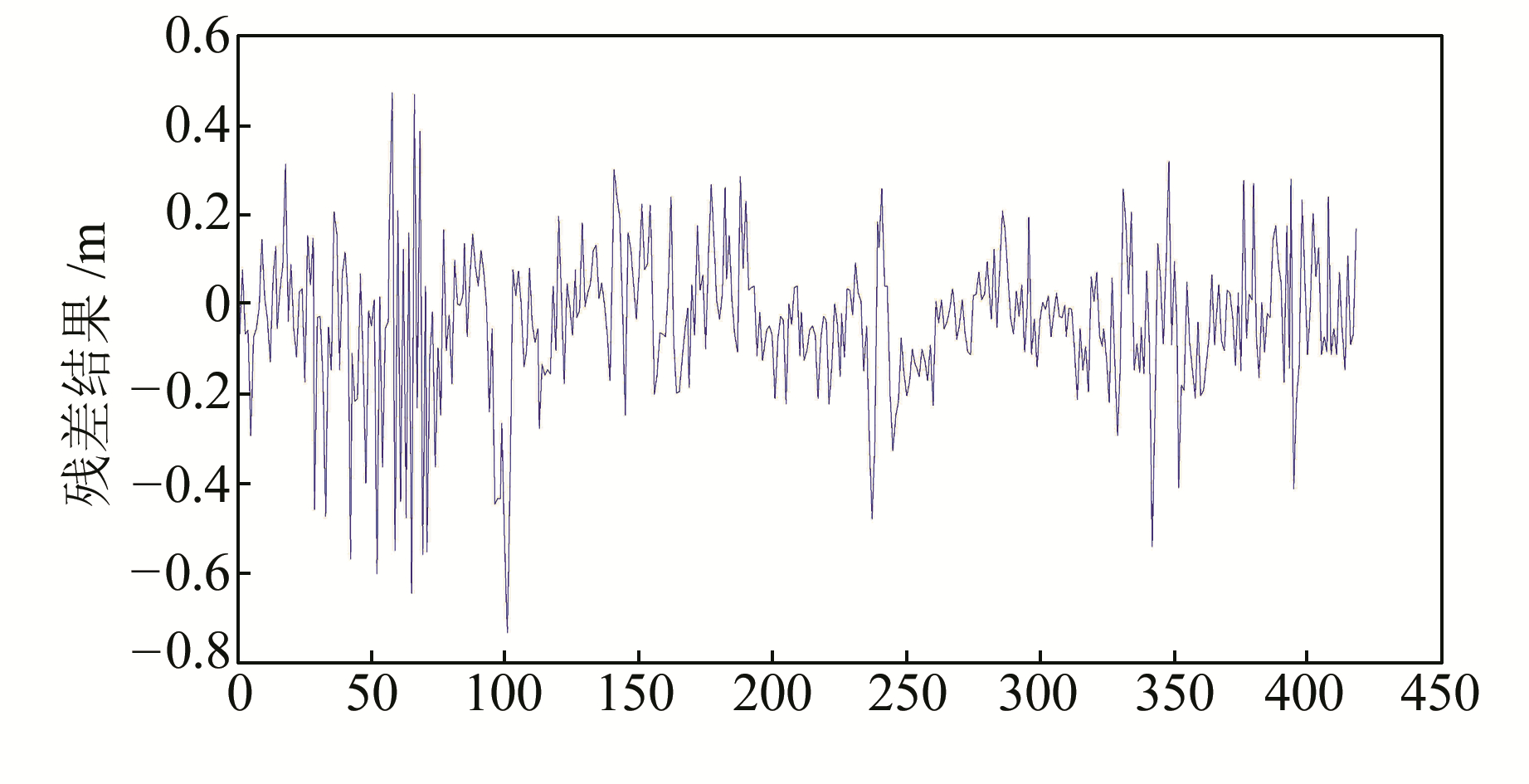
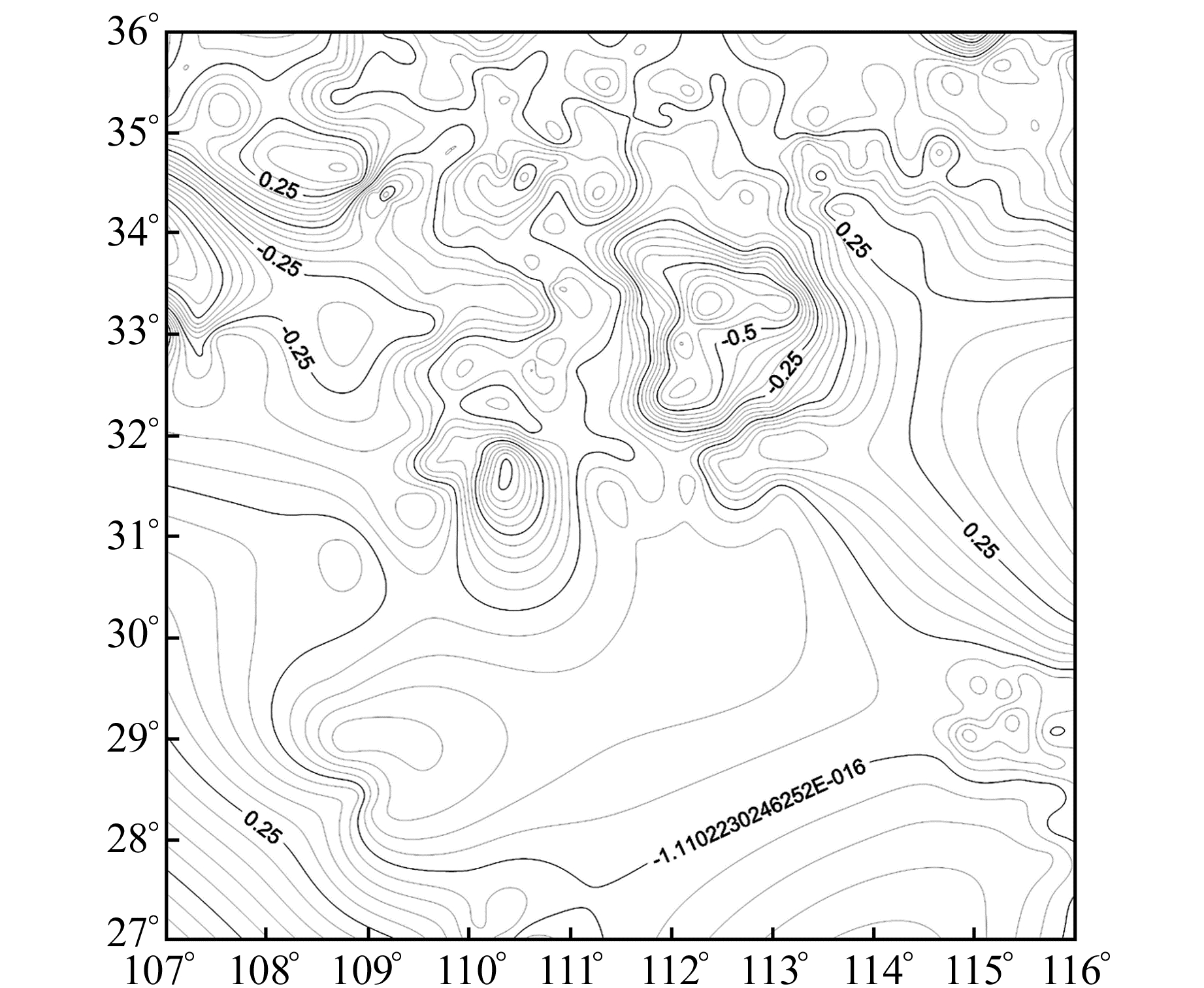
新一代高精度高程异常模型CGGM2015模型综合利用地面重力、船载重力、航空重力、卫星重力、卫星测高、陆地地形、大陆架水深、地球重力场模型、GNSS/水准、GNSS/天文等基础数据,建立了全国陆海统一的高程异常模型,中部地区高程异常精度达到±8 cm[12]。用实验区内97个GPS/水准点数据对精化的似大地水准面进行检核,表 3给出了采用不同计算方案得到的高程异常和GPS/水准点实测高程异常的比较结果。可见,与EGM2008高程异常模型相比,经过RTM改正后高程异常精度提升18%,经过残余高程异常改正后精度提升50%。图 4给出了离散检核点上的高程异常值,采用二元二次曲面函数进行拟合,图 5给出了拟合后结果,作为EGM2008+RTM高程异常模型的残余改正项。图 6给出了EGM2008+RTM+RES模型,图 7给出了其与CGGM2015模型的比较结果。可知,总体上两模型差异较小,东部和西部部分地区差异略大,约为0.8 m。
|
|
表 3 与GPS/水准数据比较结果 Tab. 3 Comparison of the results with GPS/leveling data |
|
图 4 检核点残余高程异常 Fig. 4 Residual of height anomaly of checking points |
|
图 5 残余高程异常 Fig. 5 Residual of height anomaly |
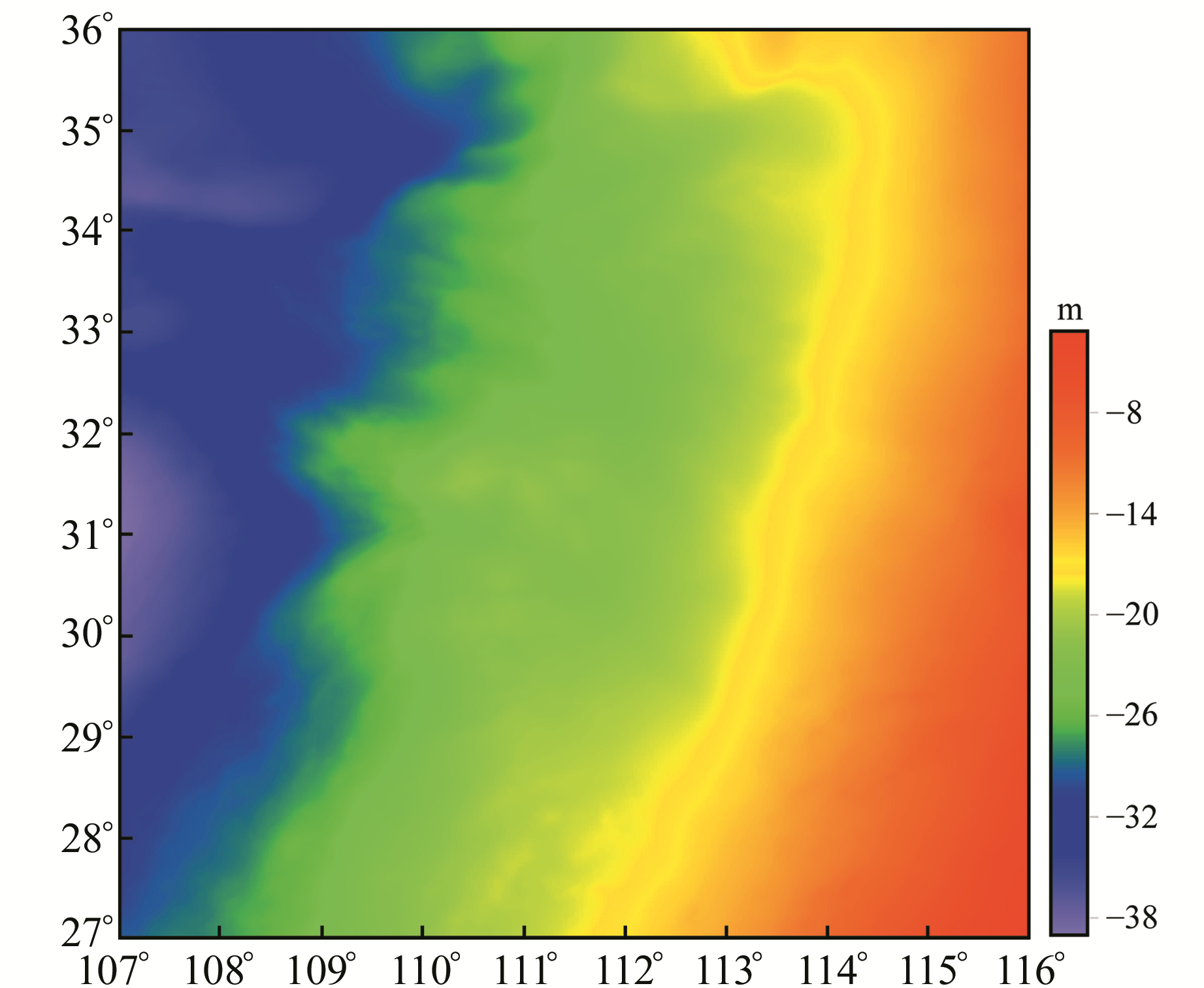
|
图 6 EGM2008+RTM+RES模型高程异常 Fig. 6 Height anomaly of EGM2008+RTM+RES |

|
图 7 高程异常比较结果(CGGM2015-(EGM2008+RTM+RES)) Fig. 7 Comparison results of height anomaly (CGGM2015-(EGM2008+RTM+RES)) |
利用DTM2006.0、SRTM模型和GPS/水准点得到剩余地形模型(RTM)高程异常和残余高程异常,将其作为改正量弥补EGM2008模型截断误差的影响,以精化局部地区大地水准面。结论如下:
1) 当积分半径内圈R1=75 km、外圈R2=200 km时,采用积分方法计算RTM高程异常模型,既能保证模型精度,又能顾及计算效率。
2) 对比EGM2008高程异常模型,当加入RTM高程异常时能够改善其精度,经检核点检验后的标准差较EGM2008结果提升18%。若顾及GPS/水准控制点的影响,对其短波项进行改进,则精度提升约50%。
3) 将改进的EGM2008+RTM+RES高程异常模型与CGGM2015模型进行比较,两者精度相当。
| [1] |
李姗姗, 吴晓平, 张传定, 等. 顾及地形与完全球面布格异常梯度项改正的区域似大地水准面精化[J]. 测绘学报, 2012, 41(4): 510-516 (Li Shanshan, Wu Xiaoping, Zhang Chuanding, et al. Regional Quasi-Geoid Refining Considering Corrections of Terrain and Complete Spherical Bouguer Anomaly's Gradient Term[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 510-516)
(  0) 0) |
| [2] |
Hirt C, Featherstone W E, Marti U. Combining EGM08 and SRTM/DTM2006.0 Residual Terrain Model Data to Improve Quasigeoid Computations in Mountainous Areas Devoid of Gravity Data[J]. Journal of Geodesy, 2010, 84(9): 557-567 DOI:10.1007/s00190-010-0395-1
(  0) 0) |
| [3] |
Hirt C. RTM Gravity Forward-Modeling Using Topography/Bathymetry Data to Improve High-Degree Global Geopotential Models in the Coastal Zone[J]. Marine Geodesy, 2013, 36(2): 183-202 DOI:10.1080/01490419.2013.779334
(  0) 0) |
| [4] |
王正涛, 党亚民, 晁定波. 超高阶地球重力场模型确定的理论与方法[M]. 北京: 测绘出版社, 2011 (Wang Zhengtao, Dang Yamin, Chao Dingbo. Theory and Methodology of Ultra-High-Degree Geopotential Model Determination[M]. Beijing: Surveying and Mapping Press, 2011)
(  0) 0) |
| [5] |
翟长治, 姚宜斌, 岳顺. 基于EGM08和剩余地形模型的区域似大地水准面精化方法[J]. 大地测量与地球动力学, 2015, 35(6): 940-944 (Zhai Changzhi, Yao Yibin, Yue Shun. Geoid Refinement Method Based on the Regional EGM08 and the Remaining Terrain Model[J]. Journal of Geodesy and Geodynamics, 2015, 35(6): 940-944)
(  0) 0) |
| [6] |
徐新强. GOCE+EGM08+RTM组合模型计算高程异常[J]. 大地测量与地球动力学, 2015, 35(5): 853-855 (Xu Xinqiang. Determination of Height Anomalies from GOCE+EGM08+RTM[J]. Journal of Geodesy and Geodynamics, 2015, 35(5): 853-855)
(  0) 0) |
| [7] |
张兴福, 刘成. 综合EGM2008模型和SRTM/DTM2006.0剩余地形模型的GPS高程转换方法[J]. 测绘学报, 2012, 41(1): 25-32 (Zhang Xingfu, Liu Cheng. The Approach of GPS Height Transformation Based on EGM2008 and SRTM/DTM2006.0 Residual Terrain Model[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 25-32)
(  0) 0) |
| [8] |
张永毅, 张兴福, 周波阳, 等. 剩余地形模型高程异常计算的积分法及精度分析[J]. 大地测量与地球动力学, 2016, 36(9): 770-775 (Zhang Yongyi, Zhang Xingfu, Zhou Boyang, et al. The Integral Method and Accuracy Analysis of Residual Terrain Model Height Anomaly[J]. Journal of Geodesy and Geodynamics, 2016, 36(9): 770-775)
(  0) 0) |
| [9] |
Hofann-Wellenhof B, Moritz H. Physical Geodesy[M]. New York: Springer, 2005
(  0) 0) |
| [10] |
Pavlis N K, Factor J K, Holmes S A. Terrain-Related Gravimetric Quantities Computed for the Next EGM[C]. The 1st International Symposium of the International Gravity Field Service (IGFS), Istanbul, 2007 http://www.researchgate.net/publication/229045443_Terrain-related_gravimetric_quantities_computed_for_the_next_EGM
(  0) 0) |
| [11] |
Frosberg R. Terrain Effects in Geoid Computations[R]. International School for the Determination and Use of the Geoid, Milano, 1994
(  0) 0) |
| [12] |
张敏利, 王强, 徐新强. 我国新一代高精度垂线偏差高程异常模型的建立[C]. 第二届中国大地测量与地球物理学学术大会, 南京, 2016 (Zhang Minli, Wang Qiang, Xu Xinqiang. Establishment of China's New Generation of High Accurate Vertical Deflection and Height Anomaly Model[C]. The 2nd Congress of China Geodesy and Geophysics, Nanjing, 2016)
(  0) 0) |
2. Xi'an Technical Division of Surveying and Mapping, 36 Xiying Road, Xi'an 710054, China
 2018, Vol. 38
2018, Vol. 38

