测绘数据处理经常涉及到三维空间坐标转换问题。当同一控制点在两套坐标系下的坐标量测值均存在误差时，可引入系数矩阵含有误差的EIV(errors-in-variables)模型求解参数^[1]。针对三维小角度坐标转换的EIV模型，陆珏等^[2]利用混合整体最小二乘(LS-TLS)算法，将系数矩阵中不需要修正的列固定，提高了参数的解算精度。袁庆等^[1]利用加权整体最小二乘(WTLS)算法，通过对系数矩阵合理地定权，将系数矩阵中不需要修正的常数项固定，得到更合适的参数解。杨仕平等^[3]考虑到系数矩阵中元素间的相关性，改进已有的加权整体最小二乘算法，通过重新构造系数矩阵的协方差阵，使相同随机元素的改正数相等，在理论上更为严密，EIV模型更加合理。但上述方法都没有顾及到在给观测向量和系数矩阵中元素定权时所选取的初始单位权方差可能不同，从而导致定权不准确的问题^[4]。

本文引用文献[5]的迭代算法，结合Helmert方差分量估计^[6]的思想，在三维小角度坐标转换模型中引入加权整体最小二乘随机模型的验后估计方法，重新分配观测向量和系数矩阵的权，使模型更加有效、合理。

1 数学模型 1.1 三维小角度坐标转换模型

假设第i个控制点在原始坐标系与目标坐标系下的坐标分别为(X_1i, Y_1i, Z_1i)、(X_2i, Y_2i, Z_2i)，则坐标转换模型可以表示为：

$ \left[ {\begin{array}{*{20}{c}} {{X_{21}}}\\ {{Y_{21}}}\\ {{Z_{21}}}\\ \vdots \\ {{X_{2k}}}\\ {{Y_{2k}}}\\ {{Z_{2k}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&{ - {Z_{11}}}&{{Y_{11}}}&{{X_{11}}}\\ 0&1&0&{{Z_{11}}}&0&{ - {X_{11}}}&{{Y_{11}}}\\ 0&0&1&{ - {Y_{11}}}&{{X_{11}}}&0&{{Z_{11}}}\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots \\ 1&0&0&0&{ - {Z_{1k}}}&{{Y_{1k}}}&{{X_{1k}}}\\ 0&1&0&{{Z_{1k}}}&0&{ - {X_{1k}}}&{{Y_{1k}}}\\ 0&0&1&{ - {Y_{1k}}}&{{X_{1k}}}&0&{{Z_{1k}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{X_0}}\\ {{Y_0}}\\ {{Z_0}}\\ {{\varepsilon _X}}\\ {{\varepsilon _Y}}\\ {{\varepsilon _Z}}\\ \mu \end{array}} \right] $

(1)

式中，k为控制点个数，(X₀, Y₀, Z₀)为平移参数，ε_X、ε_Y、ε_Z为旋转参数，μ为尺度参数。将式(1)写成矩阵形式：

$ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{A\xi }} $

(2)

由式(1)可以看出，观测向量y和系数矩阵A中的元素是相互独立的，且至少已知3个控制点在两个坐标系中的坐标，便可以求解坐标转换的7个参数。

1.2 加权整体最小二乘算法

在EIV模型中，观测向量y和系数矩阵A均包含随机误差，因此，观测方程可以定义为:

$ \mathit{\boldsymbol{y}} - {\mathit{\boldsymbol{e}}_y} = \left( {\mathit{\boldsymbol{A}} - {\mathit{\boldsymbol{E}}_A}} \right)\mathit{\boldsymbol{\xi }} $

(3)

式中，y ∈ $ \mathscr{R}$^n×1为观测向量，e_y为观测向量的随机误差，A ∈ $\mathscr{R} $^n×m为系数矩阵，rank(A)=n，E_A为系数矩阵的随机误差，ξ ∈ $\mathscr{R} $^m×1为待估参数向量。整体最小二乘的随机模型为：

$ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}_y}}\\ {{\mathit{\boldsymbol{e}}_A}} \end{array}} \right] \sim \left( {\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} 0\\ 0 \end{array}} \right],}&{\sigma _0^2\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Q}}_y}}&0\\ 0&{{\mathit{\boldsymbol{Q}}_A}} \end{array}} \right]} \end{array}} \right) $

(4)

式中，e_A=vec(E_A)，vec是矩阵列向量化算子，即e_A是将E_A列向量化得到的nm阶列向量，σ₀²为单位权方差，Q_y和Q_A分别为e_y和e_A的方差协方差矩阵。

加权整体最小二乘的平差准则为：

$ \mathit{\boldsymbol{e}}_y^{\rm{T}}{\mathit{\boldsymbol{P}}_y}{\mathit{\boldsymbol{e}}_y} + \mathit{\boldsymbol{e}}_A^{\rm{T}}{\mathit{\boldsymbol{P}}_A}{\mathit{\boldsymbol{e}}_A} = \min $

(5)

对系数矩阵和观测向量进行定权^[7]：

$ {\mathit{\boldsymbol{Q}}_A} = {\mathit{\boldsymbol{Q}}_0} \otimes {\mathit{\boldsymbol{Q}}_X} $

(6)

$ {\mathit{\boldsymbol{P}}_A} = \mathit{\boldsymbol{Q}}_A^{ - 1},{\mathit{\boldsymbol{P}}_y} = \mathit{\boldsymbol{Q}}_y^{ - 1} $

(7)

式中，Q₀和Q_X分别为系数矩阵A列向量和行向量的协因数阵，⊗为矩阵之间的Kronecker积。将P_A看成是A列向量化后的向量的权阵，便可以对A中的每一个元素定权。

由式(1)可以看出，在系数矩阵中含有一些不存在误差的常数项，若直接采用等权的TLS方法进行参数求解，则对系数矩阵中所有的元素都进行了改正，这样是不合理的^[8]。因此，给系数矩阵A赋予相应的权值Q_A^－1：

$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Q}}_{A\left( {i,j} \right)}} = }\\ {\left\{ {\begin{array}{*{20}{c}} 0&{\left( {i \ne j\;或\;i = j\;且\;{\rm{vec}}\mathit{\boldsymbol{A}}\left( i \right)为常数项} \right)}\\ {\sigma _0^2/\sigma _i^2}&{\left( {i = j\;且\;{\rm{vec}}\mathit{\boldsymbol{A}}\left( i \right)不为常数项} \right)} \end{array}} \right.} \end{array} $

(8)

式中，vecA(i)为系数矩阵列向量化后得到的向量中的第i个元素，σ_i²为原始坐标系下第i个点的坐标精度。这样计算中就不会修改系数矩阵A中的常数元素。

参数的求解过程见文献[5]。

1.3 加权整体最小二乘随机模型的验后估计

在三维小角度坐标转换中，平差模型中系数矩阵和观测向量中的元素是相互独立的，当两个坐标系中坐标的精度存在差异时，加权整体最小二乘的随机模型变为：

$ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}_y}}\\ {{\mathit{\boldsymbol{e}}_A}} \end{array}} \right] \sim \left( {\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} 0\\ 0 \end{array}} \right],}&{\left[ {\begin{array}{*{20}{c}} {\sigma _{01}^2{\mathit{\boldsymbol{Q}}_y}}&0\\ 0&{\sigma _{02}^2{\mathit{\boldsymbol{Q}}_A}} \end{array}} \right]} \end{array}} \right) $

(9)

式中，σ₀₁²为观测向量的单位权方差，σ₀₂²为系数矩阵的单位权方差。当系数矩阵和观测向量的单位权方差不相等时，在加权整体最小二乘之前给定的观测向量权阵P_y和系数矩阵权阵P_A是不恰当的，所以对这个问题必须利用平差后的结果进行处理，这就是加权整体最小二乘平差随机模型的验后估计^[4]。

在加权整体最小二乘算法的每一次迭代过程中，存在如下关系：

$ {\mathit{\boldsymbol{E}}_A} = {{\mathit{\boldsymbol{\hat E}}}_{A\left( i \right)}} $

(10)

$ \mathit{\boldsymbol{\xi }} = {{\mathit{\boldsymbol{\hat \xi }}}_{\left( i \right)}} = {\mathit{\boldsymbol{\xi }}_{\left( {i - 1} \right)}} + {\rm{ δ }}{\mathit{\boldsymbol{\hat \xi }}_{\left( i \right)}} $

(11)

代入式(3)后，展开并舍去二阶小量$ {\mathit{\boldsymbol{\hat E}}_{A\left( i \right)}}\delta {\mathit{\boldsymbol{\hat \xi }}_{\left( i \right)}}$，整理可得：

$ \mathit{\boldsymbol{y}} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{\xi }}_{\left( {i - 1} \right)}} = \mathit{\boldsymbol{A}}{\rm{ δ }}{{\mathit{\boldsymbol{\hat \xi }}}_{\left( i \right)}} - {{\mathit{\boldsymbol{\hat E}}}_{A\left( i \right)}}{\mathit{\boldsymbol{\xi }}_{\left( {i - 1} \right)}} + {\mathit{\boldsymbol{e}}_y} $

(12)

结合式(10)，改写成矩阵形式^[9]：

$ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{\xi }}_{\left( {i - 1} \right)}}}\\ 0 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{A}}&{ - \mathit{\boldsymbol{\xi }}_{\left( {i - 1} \right)}^{\rm{T}} \otimes {\mathit{\boldsymbol{I}}_n}}\\ 0&{ - {\mathit{\boldsymbol{I}}_{mn}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\rm{ δ}}{{\mathit{\boldsymbol{\hat \xi }}}_{\left( i \right)}}}\\ {{{\mathit{\boldsymbol{\hat e}}}_{A\left( i \right)}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}_y}}\\ {{\mathit{\boldsymbol{e}}_A}} \end{array}} \right] $

(13)

令B₁=[－ A    ξ_(i－1)^T  ⊗ I_n]，B₂=[0   I_mn]，L₁= A ξ_(i－1)－ y，L₂=0，$\mathit{\boldsymbol{L = }}\left[{\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{L}}_1}} \\ {{\mathit{\boldsymbol{L}}_2}} \end{array}} \right], \mathit{\boldsymbol{B = }}\left[{\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1}} \\ {{\mathit{\boldsymbol{B}}_2}} \end{array}} \right], \mathit{\boldsymbol{\hat \beta }}{\text{ = }}\left[{\begin{array}{*{20}{c}} {\delta {{\mathit{\boldsymbol{\hat \xi }}}_{\left( i \right)}}} \\ {{{\mathit{\boldsymbol{\hat e}}}_{A\left( i \right)}}} \end{array}} \right] $，权阵$\mathit{\boldsymbol{P = }}\left[{\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_y}}&0 \\ 0&{{\mathit{\boldsymbol{P}}_A}} \end{array}} \right] $，则式(13)可以表示为：

$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{e}}_y} = {\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{\hat \beta }} - {\mathit{\boldsymbol{L}}_1}\\ {\mathit{\boldsymbol{e}}_A} = {\mathit{\boldsymbol{B}}_2}\mathit{\boldsymbol{\hat \beta }} - {\mathit{\boldsymbol{L}}_2} \end{array} \right. $

(14)

此时便可以利用Helmert方差分量估计方法对加权整体最小二乘的随机模型进行验后估计。由于Helmert方差分量估计的严密公式计算非常复杂, 而且容易出现负方差分量或不收敛的情况，因此本文采用Förstner近似迭代公式^[10]计算两个方差分量的估计值：

$ \left\{ \begin{array}{l} \hat \sigma _{01}^2 = \frac{{\mathit{\boldsymbol{\hat e}}_y^{\rm{T}}{\mathit{\boldsymbol{P}}_y}{{\mathit{\boldsymbol{\hat e}}}_y}}}{{n - {\rm{tr}}\left( {{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{N}}_1}} \right)}}\\ \hat \sigma _{02}^2 = \frac{{\mathit{\boldsymbol{\hat e}}_A^{\rm{T}}{\mathit{\boldsymbol{P}}_A}{{\mathit{\boldsymbol{\hat e}}}_A}}}{{mn - {\rm{tr}}\left( {{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{N}}_2}} \right)}} \end{array} \right. $

(15)

式中，N₁= B₁^TP_y B₁，N₂= B₂^TP_A B₂，N = N₁+ N₂，tr(·)为迹算子。

利用方差分量对观测向量和系数矩阵的权阵进行修改，进而使得加权整体最小二乘的随机模型更加合理。求解过程如下^[11]：

1) 给定观测向量和系数矩阵权阵初值P_y1和P_A1，进行第一次加权整体最小二乘平差，得到待估参数${{\mathit{\boldsymbol{\hat \xi }}}_{\left( 1 \right)}} $以及改正数e_y1和e_A1；

2) 根据式(15)求得观测向量和系数矩阵的单位权方差估值$ {\left( {\hat \sigma _{01}^2} \right)_i}$和${\left( {\hat \sigma _{02}^2} \right)_i} $，并对观测向量和系数矩阵重新定权：

$ {\mathit{\boldsymbol{P}}_{{y_{i + 1}}}} = \frac{c}{{{{\left( {\hat \sigma _{01}^2} \right)}_i}}}{\mathit{\boldsymbol{P}}_{{y_i}}},{\mathit{\boldsymbol{P}}_{{A_{i + 1}}}} = \frac{c}{{{{\left( {\hat \sigma _{01}^2} \right)}_i}}}{\mathit{\boldsymbol{P}}_{{A_i}}} $

(16)

式中，c为任一常数，通常取${\left( {\hat \sigma _{01}^2} \right)_i} $或$ {\left( {\hat \sigma _{02}^2} \right)_i}$中的某个值；

3) 利用计算得到的新的权阵进行加权整体最小二乘的迭代计算；

4) 重复步骤2)、3)，当‖ ${\left( {\hat \sigma _{01}^2} \right)_i}/{\left( {\hat \sigma _{02}^2} \right)_i}-1 $‖ < δ₀且‖ $\delta {{\mathit{\boldsymbol{\hat \xi }}}_{\left( {i + 1} \right)}} $‖ < δ₀(δ₀为给定阈值，通常为10^-10)时，停止迭代。

2 算例分析

为了检验上述算法的效果，分别利用LS、TLS、WTLS以及本文提出的算法求解模拟数据，并从参数估值、均方误差等方面对结果进行对比和分析。首先给出均方误差的计算公式^[12]：

$ \begin{array}{*{20}{c}} {{\rm{MSE}} = \delta X_0^2 + \delta Y_0^2 + \delta Z_0^2 + \delta {\mu ^2}{S^2} + }\\ {\left( {\delta \varepsilon _X^2 + \delta \varepsilon _Y^2 + \delta \varepsilon _Z^2} \right)\frac{{{S^2}}}{{{\rho ^2}}}} \end{array} $

(17)

式中，δ·为各参数解与其真值之差，S为平均边长，即各控制点间距离的均值。

采用模拟的坐标数据进行解算，模拟的坐标转换参数为：(X₀, Y₀, Z₀)= (10.000 0, 10.000 0, 10.000 0)，单位为m; μ=1.01;(ε_X, ε_Y, ε_Z)=(0.02，0.05，0.08)，单位为(°)。不含误差的两套坐标系下对应点的坐标见表 1。

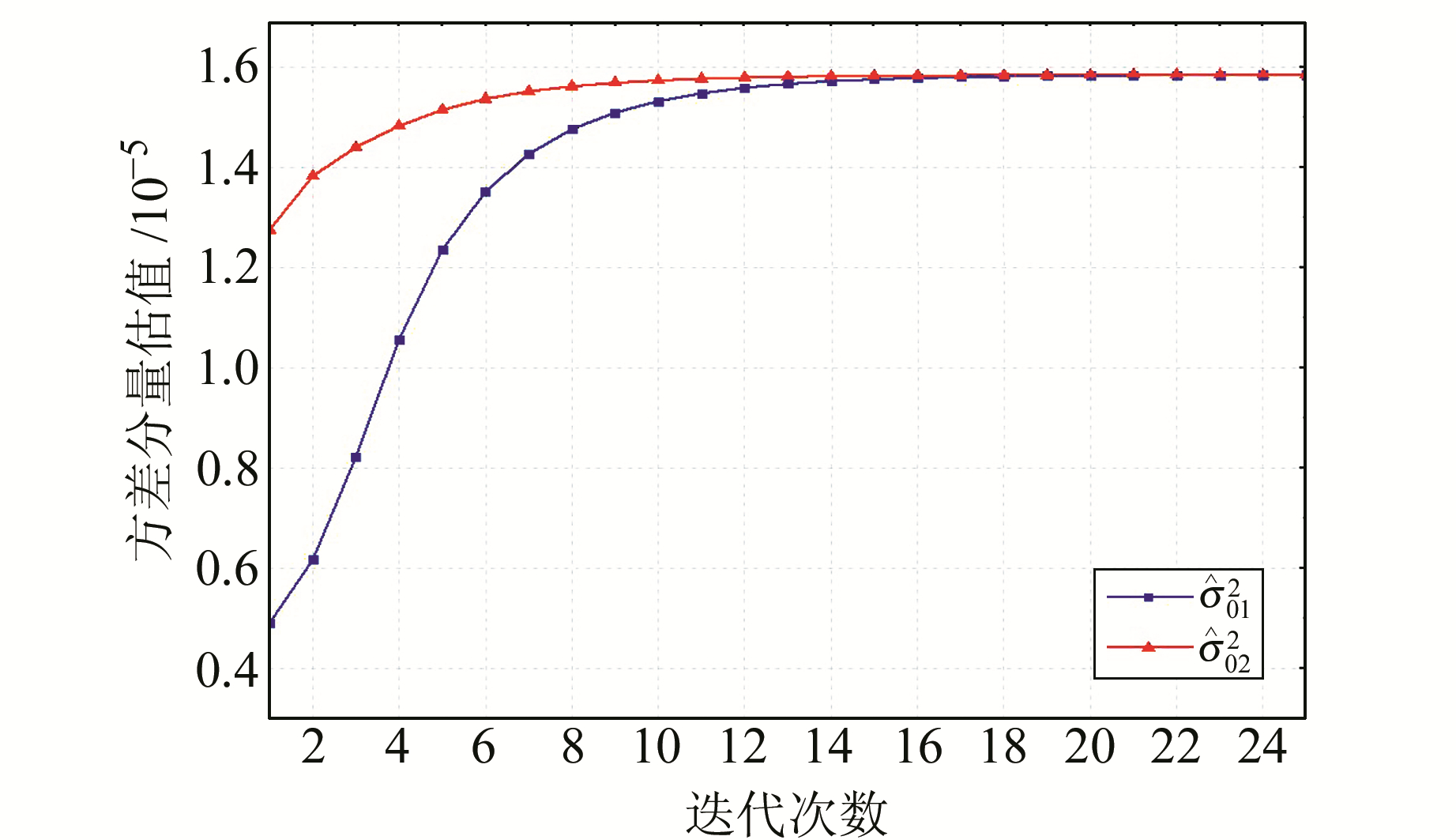
分别对原坐标系和目标坐标系下点的坐标值加入均值为0、方差为σ₀₁²Q₁和σ₀₂²Q₂的随机误差，其中σ₀₁ =0.005 m、σ₀₂ =0.001 m。一组含有误差的两个坐标系下对应点的坐标见表 2。利用本文提出的算法求解，并与LS、TLS、WTLS求解的结果进行对比。参数估值结果及均方误差见表 3。图 1为该算例中两个方差分量的收敛图。

由表 3可以看出，利用LS与TLS求解的参数估值几乎完全相同，通过WTLS方法对观测向量和系数矩阵进行合理地定权，可以提升参数估计的精确度。考虑到观测向量和系数矩阵的验前单位权方差一般不能准确已知或可能不同，利用WTLS结合Helmert方差分量估计的算法进行参数解算，参数估计的精确度得到进一步提升。

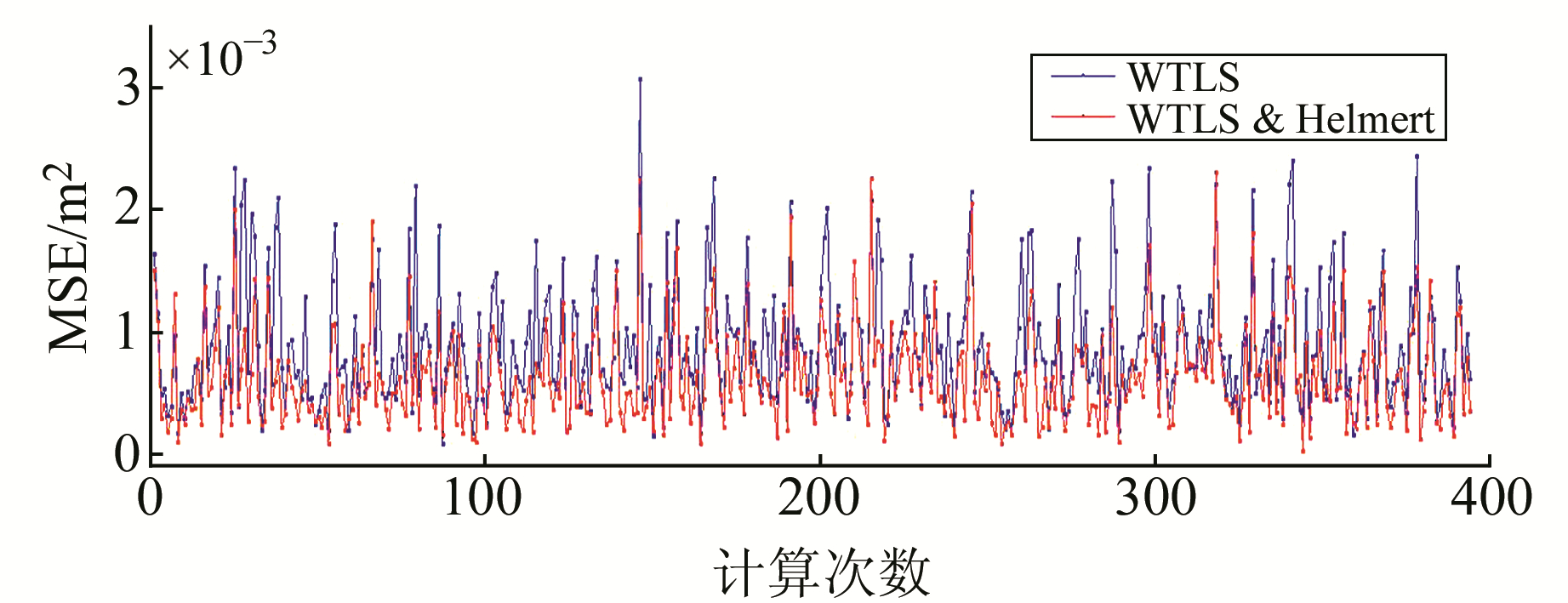
对表 1中不含误差的坐标值添加随机误差并进行500次模拟计算，分别利用WTLS及WTLS结合Helmert方差分量估计的算法求解参数估值，并计算其均方误差。除去由于迭代不收敛导致无法求解参数的情况，共得到394对模拟计算的结果(图 2)。

由图 2可以看出，通过大量的模拟计算，利用WTLS结合Helmert方差分量估计算法解算参数之后求得的均方误差普遍比WTLS算法小，说明该算法参数估计的精确度更高。经过统计，有85.5%的计算结果与上述结论相符，所以采用本文方法解算的结果更接近真值，也更为合理。

3 结语

1) 本文利用加权整体最小二乘结合Helmert方差分量估计的算法，对加权整体最小二乘的随机模型进行验后估计，通过计算得到的方差分量对观测向量和系数矩阵的权进行重新分配，使得求解的坐标转换参数精确度更高，取得了良好的效果。

2) 在对加权整体最小二乘的随机模型进行验后估计时，若采用Welsch推证的Helmert方差分量估计严密公式，在求解方差分量的迭代过程中会出现负方差分量或不收敛的情况。所以本文采用Helmert方差分量估计的近似公式进行验后估计，但仍会出现迭代不收敛的情况。因此，如何选择更加合理的验后估计算法，还有待进一步研究。