GNSS/INS组合导航以其可持续导航、高精度和高自主性,在移动测绘、地理信息采集、智能交通等城市应用中被广泛使用[1-2]。然而城市环境比较复杂,GNSS信号容易受到周围高层建筑、浓密树木、高架桥、隧道等地物的遮挡,或者多路径影响比较严重,导致GNSS信号失锁,这时只能依赖于INS导航。如果INS器件的测量精度较低,且导航时间较长,INS的导航误差就会迅速累积。里程计(OD)是一种可以自主测量车辆行驶路程/速度的器件。使用里程计辅助车载GNSS/INS组合导航,能有效解决GNSS失效情况下车辆导航系统误差快速发散的问题。
本文结合里程计刻度系数误差和IMU安装角,推导了里程计的输出模型,并结合非完整性约束对组合导航系统进行辅助,给出相应的数学模型。所谓非完整性约束,就是假定车辆在地面行驶过程中不发生侧滑或跳跃,即车辆在载体坐标系X、Z轴方向速度为0[3-4]。非完整性约束构成在X和Z方向上的速度虚拟观测量,里程计输出Y轴上的速度观测量,以此形成完整的三维速度观测,建立观测模型进行卡尔曼滤波,修正INS误差。实验结果表明,在GNSS短时失效时,里程计能有效抑制组合导航系统的误差发散,位置精度得到明显改善。
1 GNSS/INS松组合数学模型松组合是基于GNSS和INS测得的位置和速度进行组合导航的方法[5-8]。IMU采样率一般大于GNSS接收机,因此在GNSS观测不可用时,利用INS力学编排来更新状态参数中的位置、速度和姿态信息[5-8]。若GNSS观测可用,则利用GNSS与INS测得的位置和速度以闭环修正模式进行GNSS/INS松组合观测更新计算。
在GNSS/INS组合系统中,系统的状态参数x为:
| $ \mathit{\boldsymbol{x}}{\rm{ = }}{\left[{\delta {r^n}\;\;\;\;\delta {v ^n}\;\;\;\mathit{\Psi} \;\;\;{b_g}\;\;\;\;{b_a}\;\;\;\;{s_g}\;\;\;{s_a}} \right]^{\rm{T}}} $ | (1) |
式中,δrn、δvn、Ψ分别为三维位置误差、三维速度误差、三维姿态角误差,bg、ba分别为陀螺零偏和比例因子,sg、sa分别为加速度计零偏和比例因子。
GNSS/INS松组合中,通常采用卡尔曼滤波进行参数的时间更新和观测更新[5-9]。状态参数x的时间更新可表示为[5-8]:
| $ {{\mathit{\boldsymbol{\hat x}}}_k} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{k, k-1}}}}{\mathit{\boldsymbol{x}}_{k-1}} $ | (2) |
| $ {{\mathit{\boldsymbol{\hat P}}}_k} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k, k{\rm{-1}}}}{\mathit{\boldsymbol{P}}_{k-1}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k, k-1}^{\rm{T}} + {\mathit{\boldsymbol{Q}}_{k - 1}} $ | (3) |
式中,Φk, k-1为k-1时刻到k时刻的系统转移矩阵,其值由状态参数的动力学模型来决定。本文采用psi模型[5-8]来描述位置、速度和姿态变化,采用一阶高斯-马尔科夫过程[5-8]描述IMU零偏和比例因子的变化。
| $ {\mathit{\boldsymbol{x}}_k} = {{\mathit{\boldsymbol{\hat x}}}_k} + {\mathit{\boldsymbol{K}}_k}\left( {{\mathit{\boldsymbol{z}}_k}-{\mathit{\boldsymbol{H}}_k}{{\mathit{\boldsymbol{\hat x}}}_k}} \right) $ | (4) |
| $ {{\mathit{\boldsymbol{\hat P}}}_k} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k, k{\rm{-1}}}}{\mathit{\boldsymbol{P}}_{k-1}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k, k-1}^{\rm{T}} + {\mathit{\boldsymbol{Q}}_{k - 1}} $ | (5) |
式中,Kk为卡尔曼滤波增益矩阵,zk为新息向量,由INS力学编排的位置、速度与GNSS测得的位置、速度作差得到,Hk为设计矩阵,Rk为观测信息先验方差矩阵。
2 里程计辅助GNSS/INS松组合 2.1 里程计刻度系数误差里程计自身的测量误差包括环境温度、不同行驶路面条件、履带松紧和轮胎状态等引起的刻度系数的变化。用δk表示里程计刻度系数初始标定值,VOD表示里程计输出的速度,记车体坐标系为m系,并认为里程计坐标系与车体坐标系一致。在不考虑IMU与车体的安装误差角时,里程计输出的速度在IMU坐标系中的形式为:
| $ \mathit{\boldsymbol{V}}_{{\rm{OD}}}^b = \mathit{\boldsymbol{V}}_{{\rm{OD}}}^m = \left[{\begin{array}{*{20}{c}} 0\\ {\left( {1 + \delta k} \right)}\\ 0 \end{array}} \right]{\mathit{\boldsymbol{V}}_{{\rm{OD}}}} $ | (6) |
在实际应用中,很难确保IMU轴向和车体轴向一致,IMU和车体之间存在安装角。通常情况下IMU安装完成后,安装角为小角度,并且保持稳定。把INS坐标系记为b系,用Cbm表示b和m之间的姿态转换矩阵[9],则里程计的输出量在INS坐标系中的实际形式为:
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{V}}_{{\rm{OD}}}^b = {{\left( {\mathit{\boldsymbol{C}}_b^m} \right)}^{\rm{T}}} \cdot \mathit{\boldsymbol{V}}_{{\rm{OD}}}^m = {{\left( {\mathit{\boldsymbol{C}}_b^m} \right)}^{\rm{T}}}\left[{\begin{array}{*{20}{c}} 0\\ {\left( {1 + \delta k} \right)}\\ 0 \end{array}} \right]{\mathit{\boldsymbol{V}}_{{\rm{OD}}}} = }\\ {\left( {1 + \delta k} \right)\left[{\begin{array}{*{20}{c}} {-\cos \theta \sin \psi }\\ {\cos \psi \cos \theta }\\ {\sin \theta } \end{array}} \right]{\mathit{\boldsymbol{V}}_{{\rm{OD}}}}} \end{array} $ | (7) |
式中,θ为俯仰安装误差角,ψ为航向安装误差角。由式(7)可见,θ和ψ会对里程计在b系下的速度分量产生影响。因此,里程计辅助GNSS/INS组合导航在利用INS输出和里程计输出作为量测量时必须要考虑安装误差角θ和ψ的影响,否则将造成一定的误差。
2.3 里程计辅助的数学模型本文采用随机常数描述里程计刻度系数误差δk的变化,并将δk增广到状态参数中:
| $ {\mathit{\boldsymbol{x}} = {{\left[{\delta {r^n}\;\;\delta {v^n}\;\;\mathit{\Psi} \;\;\;{b_g}\;\;{b_a}\;\;\;{s_g}\;\;{s_a}\;\;\;\delta k} \right]}^{\rm{T}}}} $ | (8) |
以INS和里程计的速度之差建立量测方程,具体形式为:
| $ {\mathit{\boldsymbol{Z}} = \mathit{\boldsymbol{V}}_{{\rm{INS}}}^n-\mathit{\boldsymbol{V}}_{{\rm{OD}}}^n = \mathit{\boldsymbol{V}}_{{\rm{INS}}}^n-\mathit{\boldsymbol{C}}_b^n \cdot \mathit{\boldsymbol{V}}_{{\rm{OD}}}^b} $ | (9) |
式中,VINSn为INS推算的地理坐标系(n系)下的速度,Cbn为n系和b系之间的姿态转换矩阵。因此,GNSS可用的情况下,在位置量测方程基础上增加速度量测方程;GNSS不可用的情况下,直接使用速度量测方程,通过卡尔曼滤波参数解算,达到对INS误差积累进行修正的目的。
在GNSS可用时,位置和速度都是直接可测的参数,用卡尔曼滤波解算得到的误差改正量直接对位置和速度进行修正;在GNSS不可用时,里程计只直接测量速度,用卡尔曼滤波估计值对速度参数进行修正的结果是可靠的。但是因为随机模型的精度问题,对其他参数进行修正时,必然会存在一定的偏差。所以当GNSS不可用时,本文用正确修正后的速度重新推算位置[10]。
3 车载测试在GNSS信号有效时,组合导航系统的精度主要取决于GNSS定位的精度。因此本文在评价里程计的辅助作用时使用的策略是:仿真一系列的GNSS失锁时段,研究这些时段系统在无里程计辅助和有里程计辅助两种情况下的位置漂移,相应的位置漂移水平代表了系统的导航性能。
针对城市环境车载组合导航可能出现的GNSS失锁情况,设计两次跑车测试。第一次跑车测试用于模拟由于树木、高楼遮挡导致的短期GNSS失锁场景,地点在武汉市大花岭,环境为开阔天空,时间约为90 min。第二次跑车测试模拟由于隧道环境导致较长时间的GNSS失锁场景,测试时在武汉市某地下停车场绕行6圈,测试环境天然地隔绝了GNSS信号,时间约为10 min。跑车测试时搭载两台IMU设备,分别为武汉迈普时空导航科技有限公司的MP-POS310和MP-POS510,IMU的主要性能参数见表 1,测试设备为MP-POS310,更高精度的MP-POS510的作用是为测试提供参考真值。搭载Sicke Encoder DFS60里程计,由于测试车是前轮驱动,为避免车体转向时不符合非完整性约束,里程计安装在车辆的后轮。另外,第一次测试中使用两台Trimble R9接收机作为基准站和流动站,提供差分GNSS解。
|
|
表 1 MP-POS设备的IMU主要性能参数 Tab. 1 Technical parameters of the MP-POS310 and MP-POS510 |
对第一次跑车测试进行GNSS-PPK(post processed kinematic)解算,得到的行驶轨迹如图 1所示,图中绿色部分代表PPK解为固定解,其他颜色部分代表PPK解为浮点解或单点解。由图 1可以看出,由于测试环境开阔,PPK结果固定率很高,PPK结果与MP-POS510进行松组合,并进行反向平滑处理,可以获得较高的位置精度,将该结果作为参考真值。

|
图 1 行驶轨迹 Fig. 1 Trajectory |
为了测试里程计辅助车载组合导航系统的性能,参照轨迹图,选取PPK结果为固定解的时段,对MP-POS310采集的数据人为设置20次短期的GNSS中断,每次中断时长为60 s,考察这20次GNSS中断时组合导航系统的位置漂移。相邻两次的GNSS中断间隔至少为120 s,确保GNSS中断期间系统的位置漂移能够重新收敛。
不使用里程计辅助,对设置了GNSS中断的MP-POS310数据进行PPK松组合解算,将得到的结果与参考真值进行作差,得到的位置误差如图 2所示。使用里程计辅助,对设置了GNSS中断的MP-POS310数据进行PPK松组合解算,将得到的结果与参考真值进行作差,得到的位置误差如图 3所示。
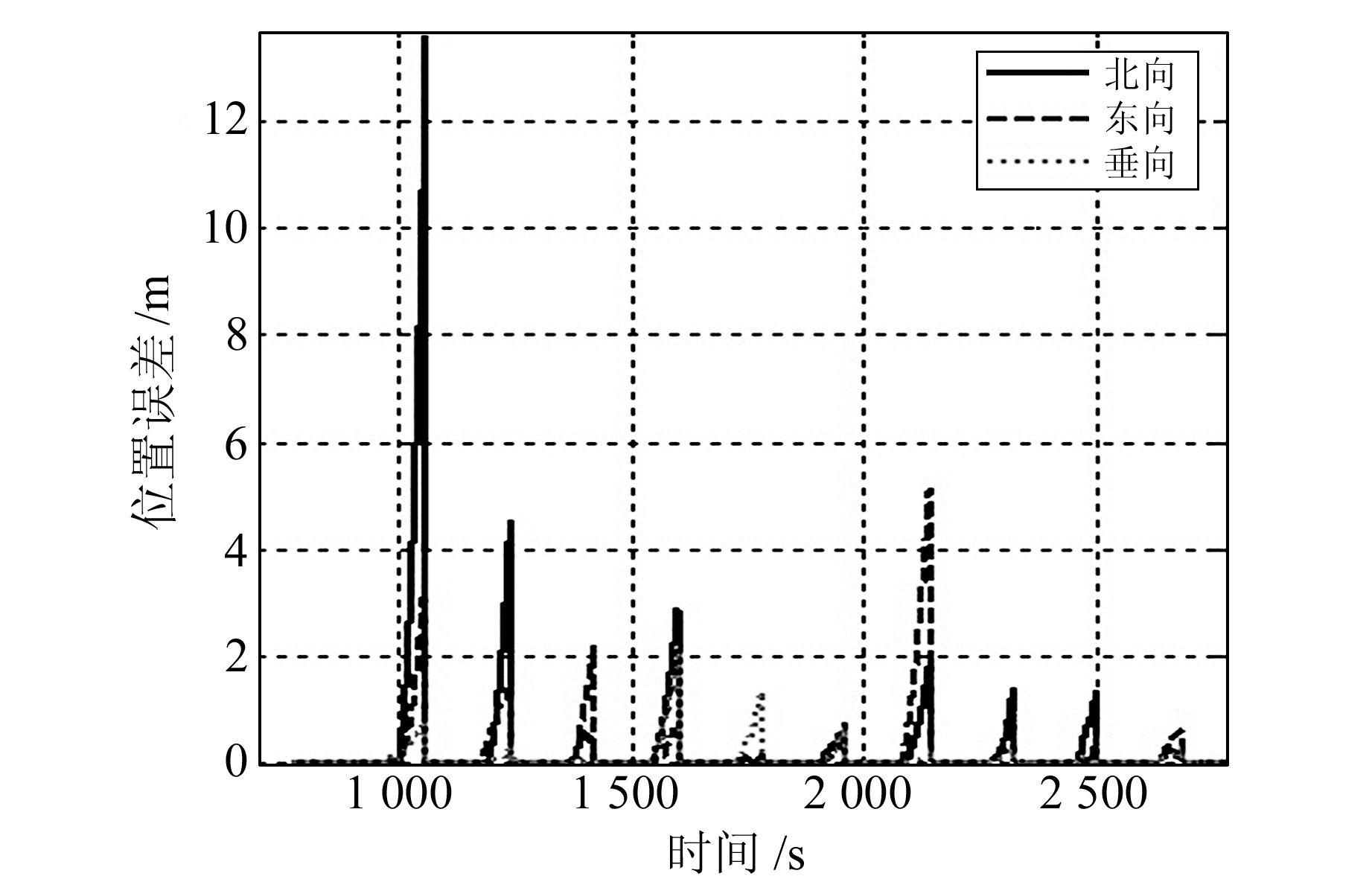
|
图 2 无辅助时的导航误差(前10次中断) Fig. 2 Navigation errors without auxiliary (only first 10 outages are shown) |
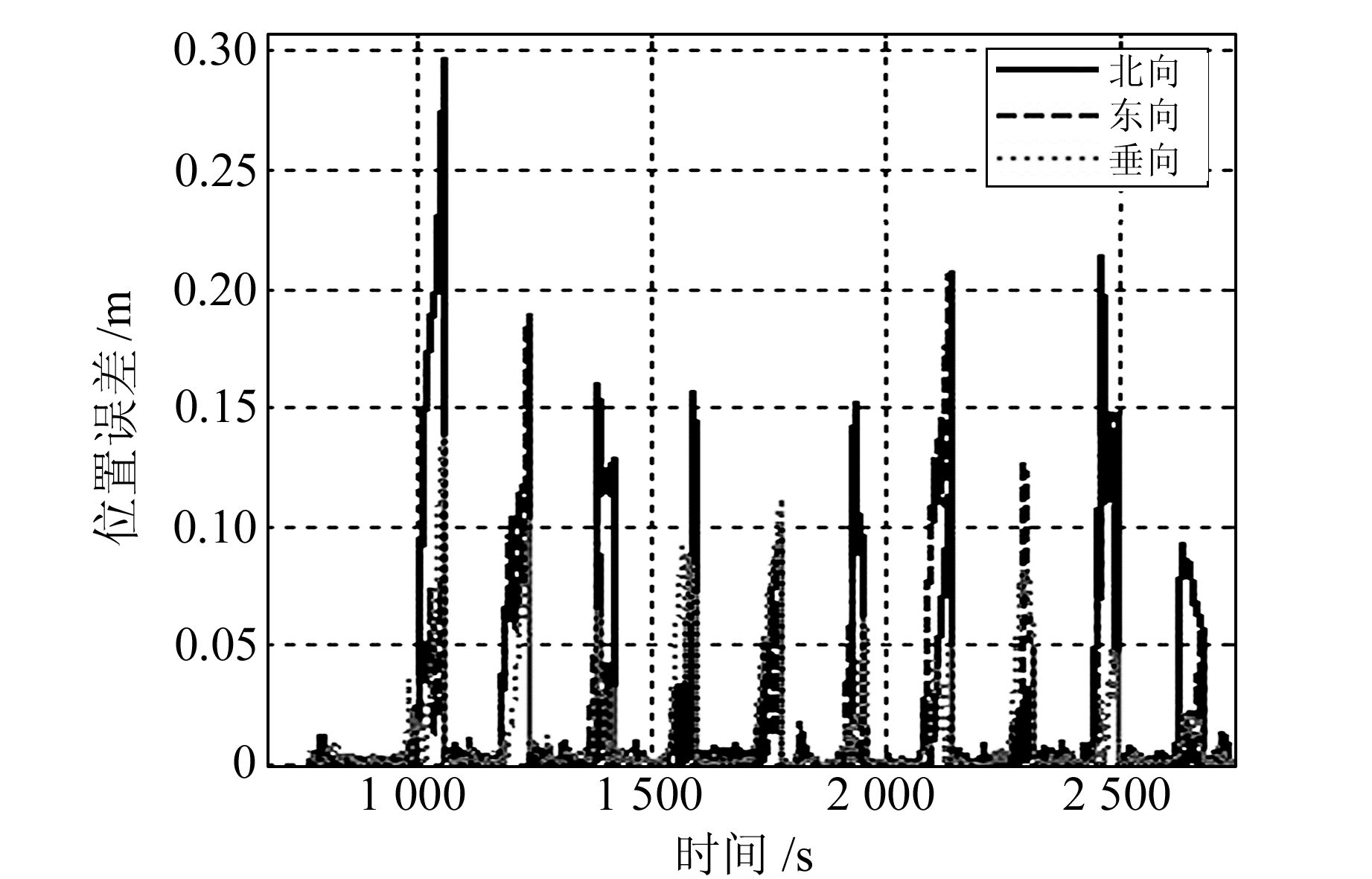
|
图 3 里程计辅助时的导航误差(前10次中断) Fig. 3 Navigation errors with OD auxiliary (only first 10 outages are shown) |
在GNSS中断时,如果没有里程计辅助,组合导航系统只有IMU单独工作。从图 2可以看出,对于MP-POS310这款中低精度的战术级IMU,60 s GNSS中断带来的位置漂移在东向、北向和垂向上都超过m级,最大的位置漂移超过10 m,这样的精度无法满足一些车载导航的应用需求。从图 3可以看出,在使用里程计辅助时,60 s GNSS中断带来的位置漂移在东向、北向和垂向上都减小至0.3 m以下,里程计对组合系统的位置精度改善效果显著。对20次GNSS中断的最大位置漂移进行统计,结果见表 2。可以看出,使用里程计辅助,60 s GNSS中断处北向、东向、垂向上的位置误差RMS由3.350 m、2.450 m、0.814 m分别减小到0.137 m、0.131 m、0.073 m,分别减小了96%、94%、91%。北向、东向和垂向上的最大位置误差由13.176 m、7.126 m、2.112 m分别减小到0.297 m、0.235 m、0.138 m,里程计辅助明显地抑制了系统导航误差的发散,组合系统的位置精度能够满足需求。
|
|
表 2 GNSS中断的位置误差统计 Tab. 2 Position errors during 60 s GNSS outage periods |
测试二在地下停车场绕行6圈,时长约10 min,测试场地天然地隔绝了GNSS信号,用于验证较长时间GNSS失锁时里程计的辅助效果。使用里程计辅助,对MP-POS510数据进行解算,解算结果的轨迹如图 4(a)所示。从图中可以看出,6次绕圈的轨迹完全重合,准确地反映了测试时的运动轨迹。这说明在10 min的GNSS中断情况下,里程计对MP-POS510这款高精度的战术级IMU有很好的辅助效果,这次解算结果可以作为参考真值,用来评估里程计对MP-POS310的辅助效果。不使用里程计辅助,对MP-POS310的数据进行解算,解算结果的轨迹如图 4(b)所示。可以看出,6次绕圈的轨迹逐次偏离,严重偏离测试的真实场景。使用里程计辅助,对MP-POS310进行解算,解算结果的轨迹图如图 4(c)所示。可以看出,6次绕圈的轨迹基本重合,对比图 4(b),里程计辅助对系统的改善效果显著,对比图 4(a),图 4(c)中左下方有部分轨迹点稍微偏离真实轨迹。表 3统计了MP-POS310两次解算与参考真值相比的最大位置误差。从表中可见,无里程计辅助时,北向、东向和垂向上的最大位置误差分别达到14 m、240 m、73 m,而使用里程计辅助后,3个方向上的最大位置误差都被抑制在5 m以下,精度提高超过90%。

|
图 4 3种松组合解算模式的轨迹 Fig. 4 Trajectories of three LC resolutions |
|
|
表 3 最大位置误差 Tab. 3 Maximum position errors |
本文研究了里程计辅助车载GNSS/INS组合导航,考虑里程计刻度系数误差和IMU安装角的影响,推导出里程计的输出模型,结合非完整性约束,给出基于卡尔曼滤波的里程计辅助的数学模型,并进行实验验证。结果表明,在GNSS中断时,里程计辅助能显著提升组合导航系统的精度,提升幅度超过90%;在搭载中低精度的战术级IMU时,GNSS短时(60 s)中断期间,里程计辅助导航误差在dm级,GNSS中断时间较长(10 min)时,里程计辅助定位误差小于5 m。
| [1] |
Titterton D H, Weston J L. 捷联惯性导航技术[M]. 北京: 国防工业出版社, 2007 (Titterton D H, Weston J L. Strapdown Inertial Navigation Technology[M]. Beijing: National Defense Industry Press, 2007)
(  0) 0) |
| [2] |
邹晓亮. 车载测量系统数据处理若干关键技术研究[D]. 郑州: 信息工程大学, 2011 (Zou Xiaoliang. Research on Key Techniques of Data Processing from Mobile Mapping System for Land Vehicle[D]. Zhengzhou: Information Engineering University, 2011) http://cdmd.cnki.com.cn/Article/CDMD-90008-1012325192.htm
(  0) 0) |
| [3] |
付强文, 秦永元, 李四海, 等. 车辆运动学约束辅助的惯性导航算法[J]. 中国惯性技术学报, 2012, 20(6): 640-643 (Fu Qiangwen, Qin Yongyuan, Li Sihai, et al. Inertial Navigation Algorithm Aided by Motion Constraints of Vehicle[J]. Journal of Chinese Inertial Technology, 2012, 20(6): 640-643)
(  0) 0) |
| [4] |
熊剑, 余恭敏, 郭杭, 等. 四轮车辆导航中的惯性/运动学模型组合方法[J]. 计算机仿真, 2014, 31(3): 188-192 (Xiong Jian, Yu Gongmin, Guo Hang, et al. Inertial/Kinematics Integrate Method for Four-Wheel Vehicle Navigation[J]. Computer Simulation, 2014, 31(3): 188-192)
(  0) 0) |
| [5] |
Shin E H. Accuracy Improvement of Low Cost INS/GPS for Land Applications[M]. Calgary: University of Calgary, 2001
(  0) 0) |
| [6] |
Shin E H. Estimation Techniques for Low-Cost Inertial Navigation[C]. UCGE Reports, Calgary, 2005 https://www.researchgate.net/publication/34178636_Estimation_techniques_for_low-cost_inertial_navigation_microform
(  0) 0) |
| [7] |
Zhang Q, Niu X J, Zhang H P, et al. Algorithm Improvement of the Low-End GNSS/INS Systems for Land Vehicles Navigation[J]. Mathematical Problems in Engineering, 2013, 1-12
(  0) 0) |
| [8] |
Niu X J, Zhang Q, Gong L L, et al. Development and Evaluation of GNSS/INS Data Processing Software for Position and Orientation Systems[J]. Survey Review, 2015, 47(341): 87-98 DOI:10.1179/1752270614Y.0000000099
(  0) 0) |
| [9] |
肖烜, 王清哲, 程远, 等. 捷联惯导系统/里程计高精度紧组合导航算法[J]. 兵工学报, 2012, 33(4): 395-400 (Xiao Xuan, Wang Qingzhe, Cheng Yuan, et al. High Accuracy Navigation Algorithm for Tightly Coupled INS/Odometer[J]. Acta Armamentarii, 2012, 33(4): 395-400)
(  0) 0) |
| [10] |
吴富梅, 杨元喜. 附加速度先验信息的车载GPS/INS/Odometer组合导航算法[J]. 宇航学报, 2010, 31(10): 2 314-2320 (Wu Fumei, Yang Yuanxi. GPS/INS/Odometer Integrated Navigation Algorithm with Prior Velocity in Land Vehicle System[J]. Journal of Astronautics, 2010, 31(10): 2 314-2320)
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38

