2. 广东省生态气象中心,广州市东莞庄路312号,510640
卫星立体观测云高反演方法已经成为一种重要的云高测量技术。Hasler等[1-3]首先尝试利用GOES静止卫星观测数据反演云顶高度,给出基于两颗静止气象卫星视云位移的云顶高度计算方法,并在两颗GOES卫星上进行反演实验,实验结果与机载激光雷达测高数据对比表明,在卫星精确定位条件下,使用水平分辨率1 km的卫星数据可以获得最高0.5 km精度的云高反演结果。Fujita等[4]和Takashima等[5]系统地研究了立体云高反演理论,利用GMS静止卫星观测数据对雷暴云团进行反演实验,并将立体云高反演技术应用于NOAA极轨卫星。Wylie等[6-7]利用GOES静止卫星在立体云高反演方面开展了大量工作,将立体方法反演结果与ER-2机载激光雷达数据进行对比,结果证明,两者在多数云区云高偏差为0.5 km左右,但是在卷云区相对偏差较大。EOS Terra卫星发射以后,Diner等[8-9]和Seiz等[10-12]利用MISR多角度探测数据进行立体云高反演研究,获得精度高达280 m的云顶高度反演结果,但是基于MISR的立体云高反演存在覆盖范围狭窄的缺点。王洪庆等[13-14]利用我国FY2和GMS静止卫星进行双星观测立体云高反演理论研究,获得了双星立体云顶高度算法模型,并对不同卫星组合的反演误差进行模拟计算分析。
我国风云静止气象卫星分配位置为86.5E、105E、112E和123E赤道上空,其中105E(实用104.5E)用于业务运行,其他用于在轨备份等用途。近年风云系列静止气象卫星已经实现双星业务观测,在双星共轭区域可同时提供两个不同方向的观测。使用风云静止气象卫星进行双星立体云高反演的条件已经成熟,但相关研究较少。本文通过研究卫星位置、视云位置、云下点位置和云顶高度之间的相互关系,推导出利用风云静止卫星双星观测数据计算真云位置和云顶高度的反演算法;然后利用推导的双星立体云高算法对视云位移分布特征以及视云位移与云高关系进行计算分析;据此提出一种非线性视云位移云高反演算法,探讨卫星数据空间分辨率对立体云高反演的影响,分析静止双星立体云高反演不同区域所能达到的云高分辨率;最后使用FY2F和FY2D双星数据进行双星立体观测云顶高度反演实验。
1 静止卫星双星观测云高算法 1.1 双星立体云高反演卫星在观测云体时,由于云团距离地面有一定高度,视云位置(云在卫星云图上出现位置)与真云位置(云下点真实位置)之间会产生视觉偏差。定义:S为卫星;C为真云(云体);V为视云(卫星云图上的投影云);G为星下点;T为云下点;O为地心;N为北极点;GV为视云大弧;TV为视云与云下点之间视真偏移大弧。地球半径在赤道附近与在极地附近略有不同,此处将地球近似为标准球体。
在静止卫星单星观测情况下,虽然视云位置V已知,但是由于视角单一,被观测云体理论上可能位于大弧GV上任何位置,因此无法从视云V地理坐标推算真云T地理坐标。考察单星观测立体几何关系可知,在视云位置、真云位置和云高3个要素中,已知任意两个要素,则第3个要素唯一确定。设(φS,θS)为卫星星下点G坐标(φ为纬度、θ为经度,下同);(φC,θC)为云下点T坐标;(φV,θV)为视云V坐标;∠NGV为视云相对卫星方位角;∠NVG为卫星相对视云方位角,则有:
| $ \left. \begin{array}{l} {\varphi _C} = \arcsin \left[{\cos TV\sin {\varphi _V}{\rm{ + }}} \right.\\ \;\;\;\;\;\;\;\;\left. {\sin TV\cos {\varphi _V}\cos \angle NVG} \right]\\ {\theta _C} = {\theta _V} \pm \arcsin \left[{\sin TV\sin \angle NVG/\cos {\varphi _C}} \right] \end{array} \right\} $ | (1) |
| $ \left. \begin{array}{l} {\varphi _V} = \arcsin \left[{\cos GV\sin {\varphi _S} + } \right.\\ \left. {\;\;\;\;\;\;\sin GV\cos {\varphi _S}\cos \angle NVG} \right]\\ {\theta _V} = {\theta _S} \pm \arcsin \left[{\sin GV\sin \angle NVG/\cos {\varphi _V}} \right] \end{array} \right\} $ | (2) |
式(1)称为真云坐标计算公式,式(2)称为视云坐标计算公式。
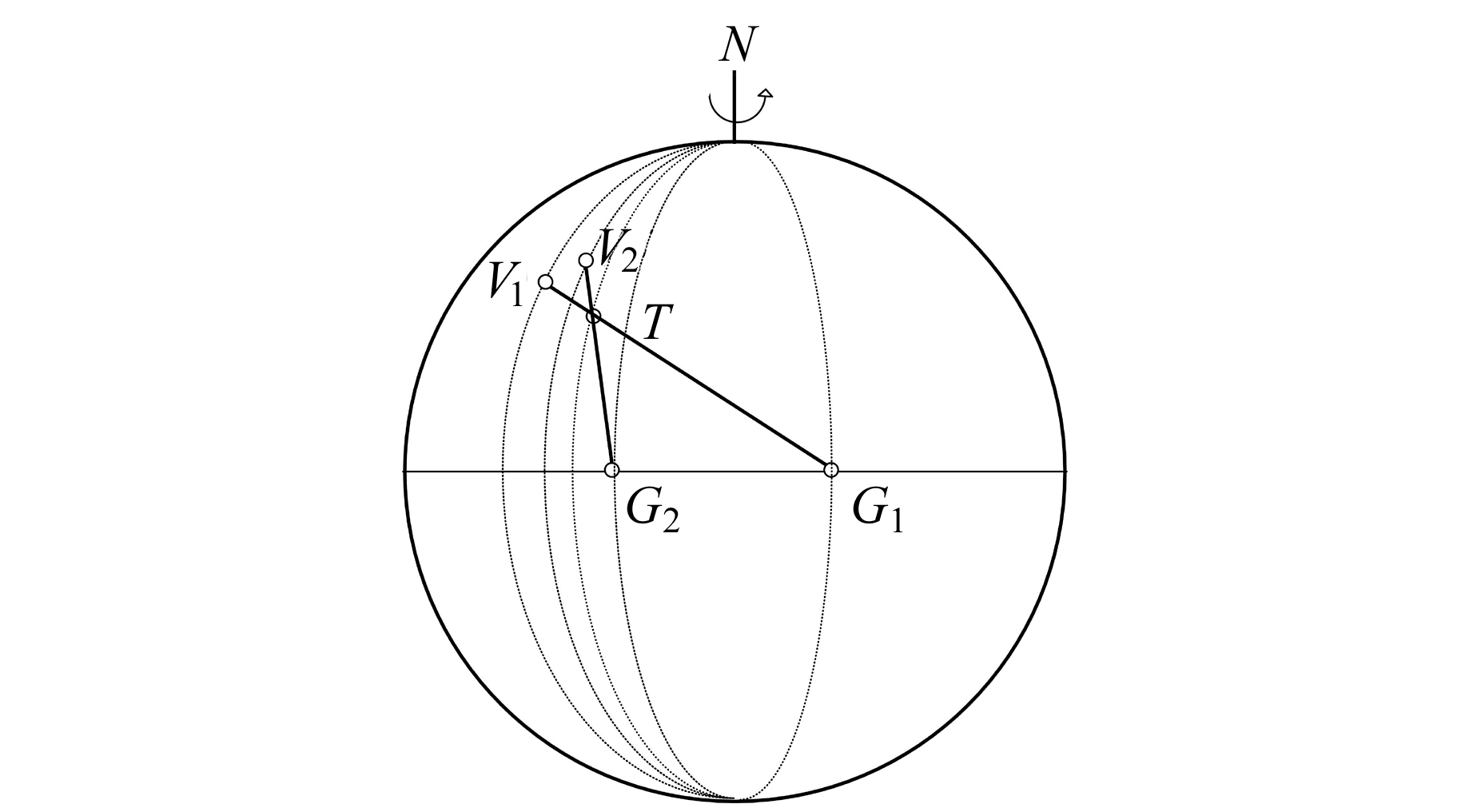
静止卫星双星立体观测示意图如图 1所示。图中,G1、G2分别为双星星下点,V1、V2分别为双星观测到的视云。真云坐标计算公式中包含云高H、云经度θC和云纬度φC共3个未知量。在一次单星观测实例中,一个视云位置建立一个观测方程无法解出3个未知量。而在一次双星同步观测实例中可以获得由两个视云位置所建立的两个观测方程,其中仍然包含3个未知量,此时观测方程可解。在两组观测方程中,两个视云地理坐标(φV1,θV1)和(φV2,θV2)为已知量,由于真云位置具有唯一性,在两组真云坐标计算公式中令两颗卫星分别测得的真云坐标相等,即φC1=φC2、θC1=θC2,理论上可解算出云高H及其真云坐标(φC,θC)。由此可见,利用双星立体观测可以同时获得云体高度和云体位置。
|
图 1 静止卫星双星立体观测示意图 Fig. 1 Geostationary satellites stereo observation |
在解云观测方程时,卫星观测数据空间分辨率和定位偏差的存在可能导致真云坐标不能严格收敛于同一坐标点上,故可以使用迭代方法解决该问题。在一次双星同步观测实例中,设定一组云高序列分别得到两组二维真云位置数据(φC1,θC1)和(φC2,θC2),由于真云位置有且仅有一个,因此在预设云高序列中存在一个高度,该高度使得对应的两个真云位置偏差具有最小值,该高度即为云顶高度,其对应的索引位置即为真云坐标。选择适当的高度迭代间距可以获得相应精度的云顶高度。
1.2 视云位移云高算法由于迭代方法效率极低,实际应用中通常采用基于视云位移与云高统计关系的经验反演算法。利用双星观测获得的两个视云坐标推算真云坐标和云高的计算过程是对真云的反演过程,而作为该反演过程的对应正演过程,可以通过真云位置和云高计算视云位置及其视云位移。使用视云计算公式分别计算双星对应视云位置V1、V2,若两个视云点的经纬度坐标分别为φV1、θV1和φV2、θV2,则视云位移P可由球面函数得到:
| $ \begin{array}{l} P = \arccos \left[{\sin {\varphi _{{V_1}}}\;\sin {\varphi _{{V_2}}} + } \right.\\ \left. {\cos {\varphi _{{V_1}}}\;\cos {\varphi _{{V_2}}}\cos \left( {{\theta _{{V_1}}}-{\theta _{{V_2}}}} \right)} \right] \end{array} $ | (3) |
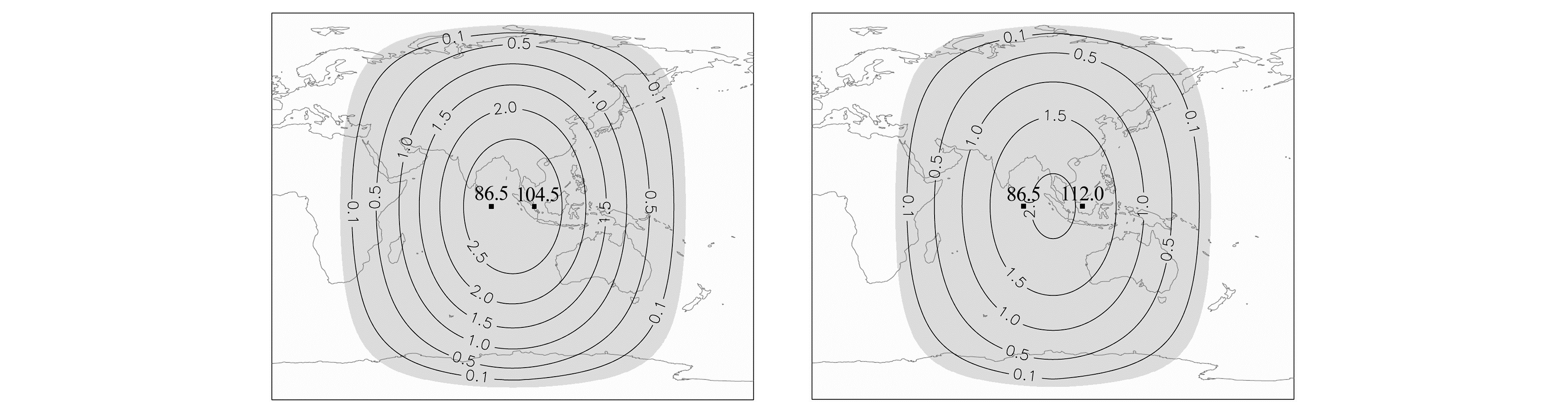
利用视云坐标及视云位移计算公式进行模拟计算,可以分析视云位移与云高相关关系以及不同云高条件下视云位移的空间分布特征。对于指定目标云,视云坐标和视云位移都是云高的单变量函数。在双星覆盖范围0.1°网格上使用视云计算公式对典型云高进行模拟计算,可以得到风云静止双星86.5E/104.5E和86.5E/112E两种组合立体观测视云位移分布。图 2(单位(°))为10 km云高视云位移(简称P10)等值线图。视云位移P10显示,在双星可观测区域,视云位移以双星星下点为中心呈现环状对称分布,其最小值出现在赤道中点附近,分别为0.03°和0.05°,最大值出现在双星共轭区域边界,分别为1.11°和1.17°,视云位移平均值分别为0.16°和0.20°。在视云位移环状分布结构中,其内圈径向梯度较小,呈现平底碗状分布特征。由于双星间距增大,86.5E/112E组合视云位移量比86.5E/104.5E组合有较大增加,说明前者更有利于双星立体云高反演的实施。

|
图 2 两种FY2组合双星观测10 km云高视云位移模拟结果 Fig. 2 10 km height cloud parallax simulate results for two FY2 pairs |
云高具有物理意义上的上限。依据世界气象组织云分类方法,将云划分为高、中、低3种类型,常见类型云体高度均处于对流层顶以下。低纬度大气对流层层顶高约为17 km,因此将云高模拟计算上限确定为20 km。使用视云位移计算公式对双星可观测范围内云高与视云位移相关关系进行模拟计算。静止卫星组合86.5E/112.0E计算结果显示,视云位移与云高呈现较好的线性关系,最小线性相关系数0.92位于双星可观测区域边沿地带,最大线性相关系数1.00位于双星赤道中点附近,全区域线性相关系数平均值为0.99。计算结果表明,在大气20 km以下有限高度区间,云顶高度H与视云位移P之间具有很好的线性关系,即H-P线性。以视云位移和云高线性相关为依据,Hasler等[1-3]利用预先计算的10 km云高位移量计算其他位移量所对应云高。若经纬度坐标(φ,θ)处云高10 km视云位移为P10,则该位置上视云位移P对应的云高H为:
| $ H = 10\left[{P\left( {\varphi, \theta } \right)/{P_{10}}\left( {\varphi, \theta } \right)} \right] $ | (4) |
根据上述分析,这种视云位移云高线性反演方法适用于大部分双星观测区域,但在边缘地带会出现较大误差。为了提高视云位移云高反演算法精度,在双星可观测范围内对视云位移云高模拟数据进行回归计算,可以得到一种H-P非线性反演算法:
| $ H = {C_1}P\left( {\varphi, \theta } \right) + {C_2}{P^2}\left( {\varphi, \theta } \right) $ | (5) |
非线性反演算法中系数C1和C2是预先回归计算生成的二维地理数组。在非线性算法中不再单纯使用P10位移量,而是使用步长为0.1 km的云高位移拟合系数作为反演系数。为了评估非线性云高反演算法模型精度改进,在双星共轭区域分别模拟计算两种模型的反演误差分布。误差分布显示,H-P线性反演算法误差从中心区域0.001 km扩大到边缘区域接近0.5 km,而H-P非线性反演算法误差整体上大幅度减小,可以将云高反演算法误差控制在10-3 km量级。
在拟定分辨率的经纬度网格上,利用双星立体观测正演方法计算不同位置上云高视云位移并经过回归计算预先获得相关系数C1和C2。在实际计算中利用该相关系数即可实现从视云位移到云高的转换。相比于真云方程高度迭代方法,视云位移云高反演方法中的系数为事先计算,因此可以更加高效地完成云高反演。
1.3 云高分辨率卫星遥感观测是在一定空间分辨率基础上进行的,基于视云位置及其视云位移计算云顶高度的双星立体云高反演必然受到空间分辨率的影响。数据空间分辨率决定了可检测的最小视云位移。由于观测数据空间分辨率的存在,视云位置与通过匹配计算获得的视云位移被量化到一定刻度,由此反演获得的云高亦相应地存在高程分辨率。双星立体观测云高分辨率反映了一个像元视云位移所能辨识的云高高程,亦即立体云高反演精度。利用视云位移云高关系模型求导计算云高分辨率:
| $ {H_{{\rm{res}}}} = \left( {{C_1} + 2{C_2}P} \right){P_{{\rm{res}}}} $ | (6) |
式中,Hres为云高分辨率,Pres为视云位移亦即观测数据分辨率,C1+2C2P为非线性反演模型导数。从式(6)看出,云高分辨率随地理位置和云高而变化。对于某一特定地理位置,C1、C2为常量,云高分辨率随视云位移而变化,意味着不同高度上具有不同的云高分辨率。由于参数C1远远大于2C2P,式(6)可近似为:
| $ {H_{{\rm{res}}}} = {C_1}{P_{{\rm{res}}}} $ | (7) |
C1是与双星间距有关的常量,增大双星间距可以减小C1,从而提高云高分辨率。需要注意到,增大双星间距虽然可以改善云高分辨率,但同时也会带来双星立体云高可反演区域的同步缩小。目前静止气象卫星观测数据支持空间分辨率为0.01°,利用Hres计算公式可以得到一个云高分辨率矩阵并据此绘制风云静止卫星两种双星组合云高分辨率分布图,如图 3所示(单位km)。云高分辨率是地理位置的函数并以双星星下点中点呈环形对称分布。考察86.5E/104.5E和86.5E/112E两种双星组合,两种组合外边界云高分辨率都为0.1 km,而中心附近分别为2.98 km和2.08 km,可反演区域云高分辨率平均值分别为1.28 km和0.93 km。西太平洋是热带气旋活跃区域,在西太平洋、印度洋、欧亚大陆东部和中国大部地区,立体云高反演方法可以实现精度为0.5~1.5 km的云顶高度反演。
|
图 3 两种FY2组合双星立体云高反演云高分辨率 Fig. 3 The stereo CTH retrieval resolution for two FY2 pairs |
使用定位于86.5E和112E赤道上空的FY2D和FY2F双星观测数据并基于视云位移云高非线性反演算法进行立体云高反演实验。FY2红外与可见光自旋扫描辐射计VISSR可见光通道空间分辨率为0.01°,其观测数据适合立体云高反演。在两幅同步观测卫星图像上,通过图像匹配技术寻找同一个云目标在两幅图像中的投影位置可获得目标云视云坐标和视云位移。为了达到图像精确匹配,卫星观测数据必须满足两个前提条件,一是观测同步,因为云顶特征和云体位置可能随时间发生变化;二是数据定位,立体云高反演基于目标云体位置和位移信息,定位误差会导致云高反演误差。
反演实验对象选择1415号台风螺旋云系,选取的观测数据为FY2F 20140912 0430UT和FY2D 20140912 0430UT两幅全圆盘可见光图像。图像数据是经过定标和定位预处理的一级标称投影数据FY2 NOM。对FY2F和FY2D双星VISSR VIS通道1 km数据进行相同区域相同类型局地地图投影,像元分辨率统一取0.01°×0.01°。图像投影过程中需要进行定位校正,可以采用地面控制点等措施进行地理订正。将FY2立体云高反演结果与Cloudsat云廓线雷达CPR观测结果进行对比验证。CPR廓线数据选取CPR 2014255035311 2BGEOPROF GRANULE 44549轨道块,该轨道块上CPR对于实验对象观测时间与FY2 VISSR扫描时间之间相差仅数分钟,两者具有较好可比性。
2.2 云高反演首先选择目标云块。在FY2F图像中选定目标云块,在FY2D图像中寻找匹配云块。反演实验使用的云块为20像元×20像元,匹配窗口大小选择需要有利于达成图像匹配计算,窗口过小则包含的云块特征不足,窗口过大则可能导致目标云块在高度属性上出现较大不一致性,两种情况都会带来过多的失配或错配从而影响图像匹配的效果。
其次进行图像匹配计算。逐一提取FY2F目标云块并在FY2D图像中进行图像匹配计算以获得视云坐标和视云位移。图像匹配算法采用Pierson矩阵相关系数,使用协方差与标准偏差的组合形式。匹配门槛设置为0.95,低于该阈值则标记失配。搜索窗口半径取决于目标云所在位置的视云位移最大值,对于86.5E/112E双星组合,搜索窗口统一使用0.2°半径。在搜索窗口中建立匹配窗口与目标窗口进行相关性计算,得到一个相关系数矩阵,当相关系数矩阵最大值大于0.95时,则该最大值对应窗口即为配准窗口,窗口中心点所在位置即为目标云在FY2D图像中的视云位置,由此计算得到目标云视云位移。
最后完成立体云高反演。使用视云位移云高非线性反演算法计算云顶高度。需要注意到,部分目标云块可能会出现匹配失配而无法获得云高的情况。
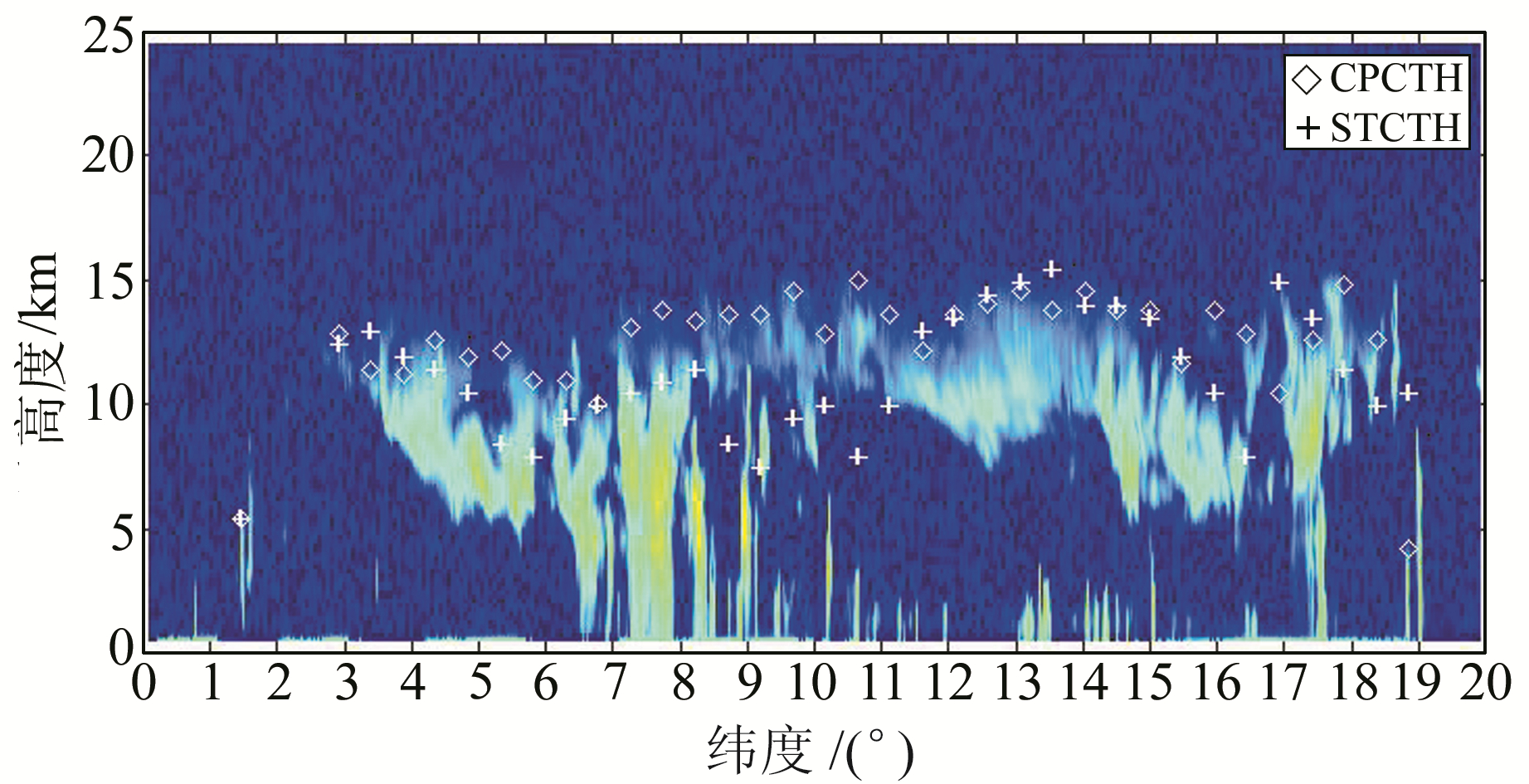
2.3 结果分析FY2D和FY2F由北向南全圆盘扫描时间为25 min,对台风观测时间约为0445UT。与此同时,Cloudsat穿越赤道由南向北划过台风东侧螺旋云系,0443UT~0448UT时段Cloudsat星下点移动路径自北纬0°向20°,FY2双星和Cloudsat对0°~20°区域观测时差仅为数min,可使用Cloudsat云廓线雷达CPR云高测量结果对双星立体云高进行真实性检验。CPR 2B-GEOPROF产品包含地理定位、廓线高程、回波强度和云检测数据。CPR云检测识别编码0~40序列号中20~40为云识别编码,每条有云廓线自上而下首个云样本所对应的高度为云顶高度。CPR垂直分辨率为240 m,垂直廓线样本沿雷达行进轨迹方向为1.1 km水平间距。以水平间距50样本对CPR轨迹进行抽样得到50 km间距轨迹子集,依照轨迹子集进行立体云高反演并与CPR云高进行对比分析,如图 4所示。图中以CPR雷达回波强度为背景绘制云高对比标记,其中CPCTH表示CPR测量的云高结果,STCTH表示双星立体方法反演得到的云顶高度。
|
图 4 沿CPR轨迹立体云高反演实验结果 Fig. 4 The stereo CTH results along CPR track |
云高对比结果表明,此次反演实验STCTH与CPCTH平均绝对偏差为2.3 km,大于理论误差1.5 km。对于云顶比较密实的目标云反演效果较好,误差在1 km左右,例如12~15°N和4~5°N附近。在透明云块或高层薄云下存在低层云的情况下,会出现失配或匹配到低层云,从而引起较大误差,例如8~11°N和16~19°N附近。这是由于云体在多层并且透明条件下其图像特征随观测角度不同发生显著变化,从而导致图像匹配困难并可能低估高层云高度。实验发现,传感器数值分辨率量化会对图像匹配准确性带来一定影响。VISSR-F传感器性能相对较好,VISSR-D常常在反射率较高的密实云顶过早进入饱和状态,图像灰阶差别会衰减匹配系数使得匹配率下降。反演实验说明,立体云高反演方法对于多层透明云会产生较大不确定性,同时证明图像匹配技术对于立体云高反演的重要性。
3 结语两颗静止卫星对同一云目标可以同时提供两个视角遥感观测,利用一次双星同步观测可同时解算出云顶高度和云下点坐标。本文通过对视云位移和云高模拟计算分析,提出一种视云位移、云高非线性反演算法。计算表明,该方法反演精度优于Hasler等[1-3]的线性算法模型。风云静止卫星双星组合86.5E/112E在视云位移和云高分辨率两个方面都比86.5E/104.5E组合有较大提高,说明前者更有利于静止双星立体云高反演的实施。在观测数据分辨率为0.01°情况下,静止双星组合86.5E/112E平均云高反演精度理论上可以达到0.93 km。虽然增大双星间距有利于提高云高反演精度,但同时也会导致立体云高可反演区域缩小。
本文使用FY2D和FY2F双星数据进行双星立体云高反演实验。实验地点在西北太平洋,反演对象为1415号台风螺旋云带,沿Cloudsat轨迹进行双星立体云高反演并与CPR微波雷达云高测量结果对比,在密实云顶两者平均偏差为1 km,总样本平均绝对偏差为2.3 km。反演实验结果与Hasler和Wylie等基于GOES卫星的立体云高反演精度(密实云顶和总样本偏差分别为0.5 km和2 km)存在差别,原因可能是进行精度检验所采用的参考数据来源不同。
云顶高度对于卫星云迹风在数值预报中的应用至关重要。由于红外云高反演方法效果并不理想,许健民等[15-16]和Menzel等[17-18]建议在云顶高度反演中开展非物理方法技术研究。尽管卫星立体云高反演技术在精度上与激光雷达或微波雷达相比存在差距,但是立体云高反演技术具有可同时提供大范围云高数据的优势。随着静止气象卫星更新换代,其定位精度和空间分辨率提高,有利于卫星立体云高反演技术进入业务应用。关于风云静止卫星立体云高反演,本文主要研究了双星立体云高反演算法并进行初步反演实验,未来还需要更多实例分析和多种观测手段进行横向对比。
| [1] |
Hasler A F. Stereographic Observations from Geosynchronous Satellites: An Important New Tool for the Atmospheric Sciences[J]. Bulletin of the American Meteorological Society, 1981, 62(2): 194-212 DOI:10.1175/1520-0477(1981)062<0194:SOFGSA>2.0.CO;2
(  0) 0) |
| [2] |
Hasler A F, Mack R, Negri A. Stereoscopic Observations from Meteorological Satellites[J]. Advances in Space Research, 1983, 2(6): 105-113 DOI:10.1016/0273-1177(82)90130-2
(  0) 0) |
| [3] |
Hasler A F, Strong J, Woodward R H, et al. Automatic Analysis of Stereoscopic Satellite Image Pairs for Determination of Cloud-Top Height and Structure[J]. Journal of Applied Meteorology, 1991, 30(3): 257-281 DOI:10.1175/1520-0450(1991)030<0257:AAOSSI>2.0.CO;2
(  0) 0) |
| [4] |
Fujita T T. Principle of Stereoscopic Height Computations and Their Applications to Stratospheric Cirrus over Severe Thunderstorms[J]. Journal of the Meteorological Society of Japan, 1982, 60(1): 355-368 DOI:10.2151/jmsj1965.60.1_355
(  0) 0) |
| [5] |
Takashima T, Takayama Y, Matsuura K, et al. Cloud Height Determination by Satellite Stereography[J]. Papers in Meteorology and Geophysics, 1982, 33(2): 65-78 DOI:10.2467/mripapers.33.65
(  0) 0) |
| [6] |
Wylie D P, Menzel W P, Woolf H M, et al. Four Years of Global Cirrus Cloud Statistics Using HIRS[J]. Journal of Climate, 1994, 7(12): 1 972-1986 DOI:10.1175/1520-0442(1994)007<1972:FYOGCC>2.0.CO;2
(  0) 0) |
| [7] |
Wylie D P, Santek D, Starr D O C. Cloud-Top Heights from GOES-8 and GOES-9 Stereoscopic Imagery[J]. Journal of Applied Meteorology, 1998, 37(4): 405-413 DOI:10.1175/1520-0450(1998)037<0405:CTHFGA>2.0.CO;2
(  0) 0) |
| [8] |
Diner D J, Davies R, Di Girolamo L, et al. MISR Level 2 Cloud Detection and Classification Algorithm Theoretical Basis[J]. Jet Propulsion Laboratory, Pasadena, 1996
(  0) 0) |
| [9] |
Diner D J, Di Girolamo L, Clothiaux E. MISR Level 1 Cloud Detection Algorithm Theoretical Basis[J]. Jet Propulsion Laboratory, Pasadena, 1999
(  0) 0) |
| [10] |
Seiz G, Davies R, Grün A. Stereo Cloud-Top Height Retrieval with ASTER and MISR[J]. International Journal of Remote Sensing, 2006, 27(9): 1 839-1853 DOI:10.1080/01431160500380703
(  0) 0) |
| [11] |
Seiz G, Tjemkes S, Watts P. Multi-View Cloud-Top Height and Wind Retrieval with Photogrammetric Methods: Application to Meteosat-8 HRV Observations[J]. Journal of Applied Meteorology and Climatology, 2007, 46(8): 1 182-1195 DOI:10.1175/JAM2532.1
(  0) 0) |
| [12] |
Seiz G, Baltsavias E P, Gruen A. Comparison of Satellite-Based Cloud-Top Height and Wind from MISR, ATSR2 and Meteosat-6 Rapid Scans [C]. EUMETSAT Users' Conference, Antalya, 2001
(  0) 0) |
| [13] |
Wang H Q, Lu S H, Zhang Y, et al. Determination of Cloud Top Height from Stereoscopic Observation[J]. Progress in Natural Science, 2002, 12(9): 689-694
(  0) 0) |
| [14] |
王洪庆, 吕胜辉, 张焱, 等. 双星立体观测的云顶高度反演[C]. 中国气象学会2003年年会论文集, 2003 (Wang Hongqing, Lü Shenghui, Zhang Yan, et al. The Retrieval of Cloud-Top Height from Stereoscopic Observation [C]. China Meteorological Society Conference Proceedings, 2003)
(  0) 0) |
| [15] |
许健民, 张其松, 方翔. 用红外和水汽两个通道的卫星测值指定云迹风的高度[J]. 气象学报, 1997, 55(4): 408-417 (Xu Jianmin, Zhang Qisong, Fang Xiang. Height Assignment of Cloud Motion Winds with Infrared and Water Vapor Channels[J]. Acta Meteorological Sinica, 1997, 55(4): 408-417 DOI:10.11676/qxxb1997.041)
(  0) 0) |
| [16] |
许健民, 张其松. 卫星风推导和应用综述[J]. 应用气象学报, 2006, 17(5): 574-582 (Xu Jianmin, Zhang Qisong. Status Review on Atmospheric Motion Vectors Derivation and Application[J]. Journal of Applied Meteorological Science, 2006, 17(5): 574-582 DOI:10.11898/1001-7313.20060515)
(  0) 0) |
| [17] |
Menzel W P, Frey R A, Zhang H, et al. MODIS Global Cloud-Top Pressure and Amount Estimation: Algorithm Description and Results[J]. Journal of Applied Meteorology and Climatology, 2008, 47(4): 1 175-1198 DOI:10.1175/2007JAMC1705.1
(  0) 0) |
| [18] |
Menzel W P, Frey R A, Bryan A B. Cloud Top Properties and Cloud Phase Algorithm Theoretical Basis Document [M]. Madison: University of Wisconsin-Madison, 2010
(  0) 0) |
2. Guangdong Ecological Meteorology Center, 312 Dongguanzhuang Road, Guangzhou 510640, China
 2018, Vol. 38
2018, Vol. 38

