截至2016-12已有6颗BDS-3卫星相继发射入轨,包括1颗GEO卫星(C17)、2颗IGSO卫星(C31和C32)以及3颗MEO卫星(C33、C34和C35)。存在于BDS-2卫星伪距观测值中的伪距多路径偏差已被证实与卫星类型、高度角及信号频率有关,该偏差对定位精度及模糊度固定有较大影响[1-4]。Wanninger等[5]提出根据BDS-2卫星高度角进行偏差改正的模型,有效地削弱了伪距多路径偏差的影响。而目前尚无针对BDS-3卫星的伪距多路径偏差的研究。由于C17和C35卫星仍处于调试阶段,本文只分析剩余4颗BDS-3卫星的卫星端伪距多路径偏差的特性。
1 分析方法BDS-2卫星可发射3个频率信号(B1、B2和B3), 而BDS-3卫星(C32、C33、C34和C35)可发射5个(B1、B2a、B3、B1c和B2b,表 1)[6]。对于C31卫星,接收机仅能捕获B1和B3频率的观测数据。
|
|
表 1 BDS-3卫星的信号频率 Tab. 1 Navigation signals of the BDS-3 satellites |
利用伪距多路径组合(MP)观测值序列提取的多路径误差包括伪距多路径和观测噪声偏差,主要通过单频伪距观测值和双频相位观测值组合得到[7]:
| $ {\rm{M}}{{\rm{P}}_i} = {P_i} + \left( {{m_{ijk}}-1} \right){\varphi _i}-{m_{ijk}}{\varphi _j}-B $ | (1) |
式中,
通过式(1)分别计算BDS-3每颗卫星的MP组合,并以高度角为自变量进行三次多项式拟合,建立以高度角为输入的新卫星的伪距多路径偏差模型[9-10]:
| $ \begin{array}{l} {\rm{M}}{{\rm{P}}_i}\left( j \right) = {A_0} + {A_1}E\left( j \right) + \\ {A_2}E{\left( j \right)^2} + {A_3}E{\left( j \right)^3} \end{array} $ | (2) |
式中,E(j)为第j个高度角值,MPi(j)为对应的MP组合值,A0、A1、A2、A3为三次多项式的拟合参数。
GEO卫星的高度角变化范围较小,难以确定其伪距观测值是否受到与高度角相关的伪距多路径偏差的影响,因此本文仅分析IGSO和MEO卫星的伪距多路径偏差特征。
2 BDS-2卫星伪距多路径偏差分析图 1给出了JFNG测站2016-07-01 IGSO(C06~10)和MEO卫星(C11、C12和C14)的MP序列。可以看出,BDS-2卫星存在与高度角大小相关的伪距多路径偏差,且随着高度角的增大而逐渐减小,相同类型的卫星对应的偏差基本吻合;MEO卫星比IGSO卫星的偏差更显著;不同频率上的偏差有所区别,B1频率的偏差大于B2和B3。

|
图 1 BDS-2 IGSO和MEO卫星在B1、B2和B3频率上的MP序列 Fig. 1 The MP series over elevation angles for BDS-2 IGSO and MEO satellites on B1, B2 and B3 frequency |
图 2给出了伪距多路径偏差改正后的MP序列与高度角的关系。可见,改正伪距多路径偏差后,北斗卫星的MP序列与高度角没有明显的数值关系,仅呈现低高度角时影响较明显、高高度角时影响较弱。

|
图 2 伪距多路径偏差改正后的BDS-2 IGSO和MEO卫星在B1、B2和B3频率上的MP序列 Fig. 2 The corrected MP series over elevation angles for BDS-2 IGSO and MEO satellites on B1, B2 and B3 frequency |
2016-03-30 BDS-2的C15卫星成功入轨,完成测试后与其他卫星共同提供服务。本文计算伪距多路径偏差改正前后的C15卫星的MP组合,以验证该卫星是否仍存在偏差及该偏差能否被现有的模型进行改正。
MGEX测站仅提供B1和B2两个频率的数据,图 3给出了JFNG测站2016-07-01伪距多路径偏差改正前后的MP1和MP2序列与高度角的关系。可以看出,MP组合仍存在明显的偏差,该偏差随高度角的增大而减小,与其他BDS-2卫星MP序列的变化趋势一致。采用伪距多路径偏差改正模型进行改正后,C15卫星的伪距多路径偏差得以消除。
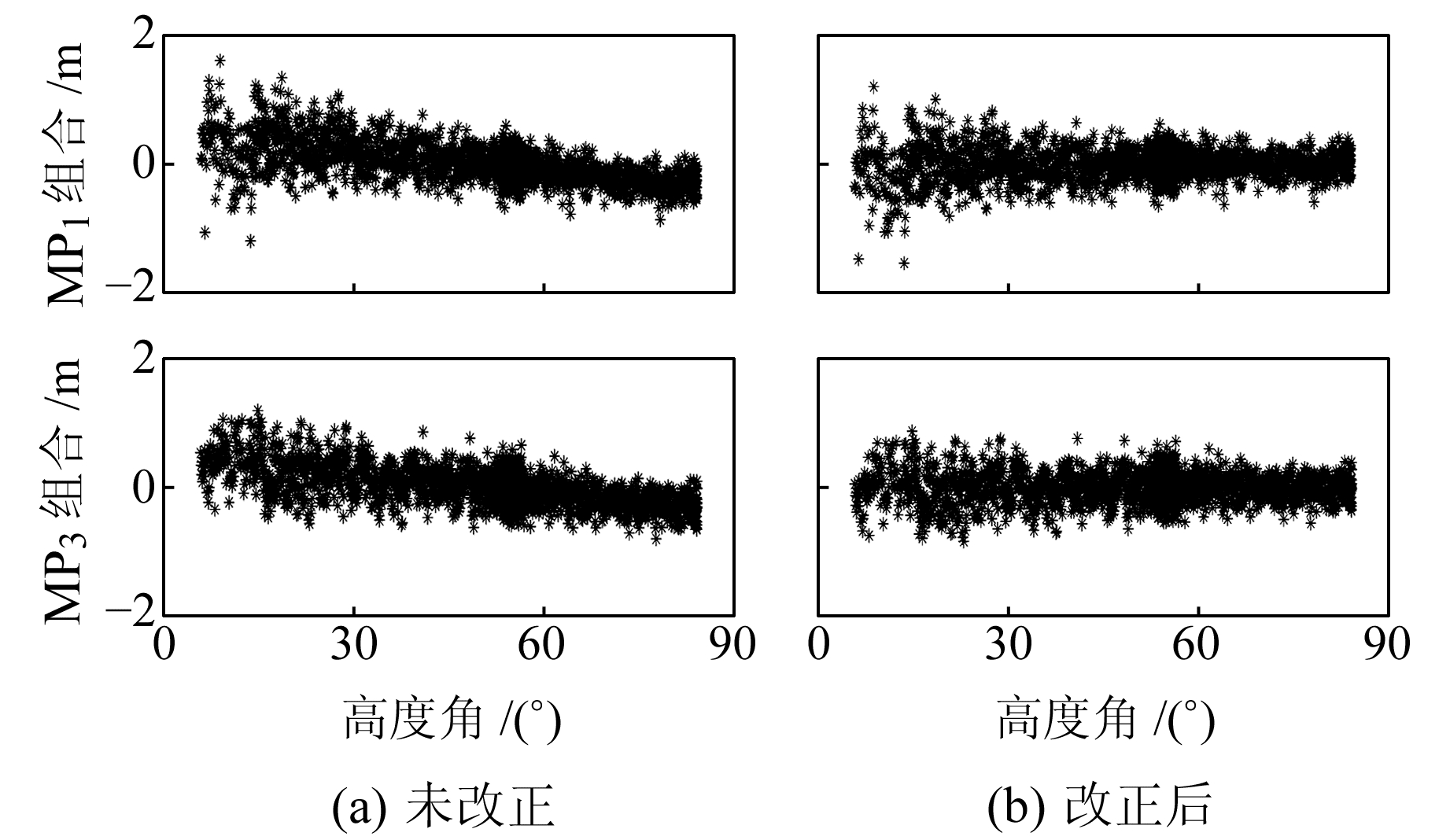
|
图 3 伪距多路径偏差改正前后的BDS-2 C15卫星MP序列与高度角关系 Fig. 3 The MP series over elevation angles for BDS-2 C15 satellite before and after the code bias corrected |
2016-07-10~08-10在武汉大学测绘学院楼顶进行实验数据采集,采样间隔30 s,在数据处理之前对周跳进行探测和修复。实验阶段C31卫星仅有B1和B3两个频率的观测数据,图 4给出了C31卫星的伪距多路径偏差和高度角的关系,三次多项式拟合系数见表 2。由图 4看出,BDS-3的C31卫星的MP序列特征呈零均值,与高度角不相关。表 2的多项式拟合参数均接近0,尤其是A0和A1,为mm级,在图 4中为接近0的直线。
|
|
表 2 BDS-3 C31卫星MP序列三次多项式拟合参数 Tab. 2 Cubic polynomial fitting parameters of MP series for BDS-3 C31 satellite |
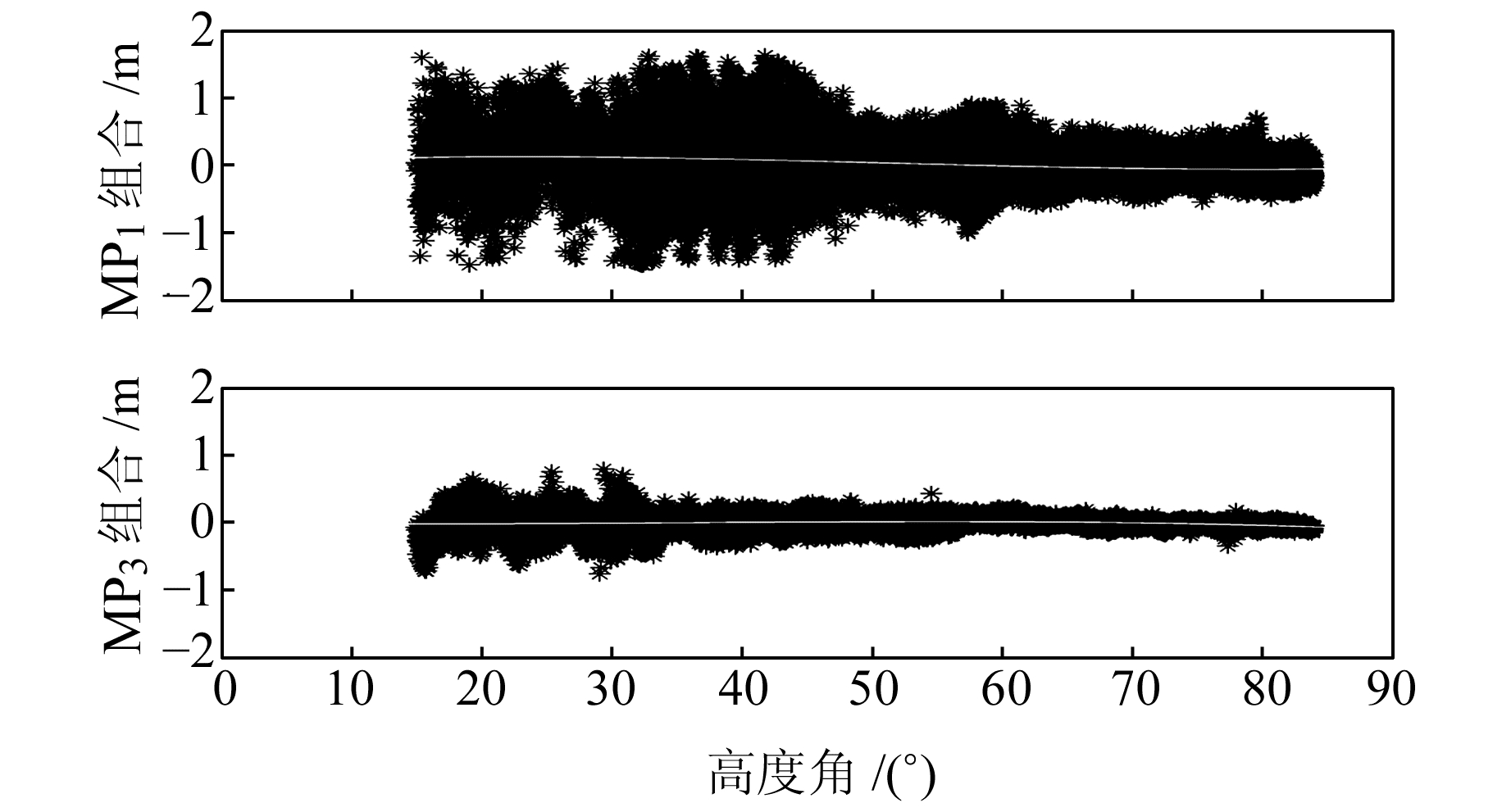
|
图 4 BDS-3 C31卫星MP序列与高度角关系 Fig. 4 The MP series over elevation angles for BDS-3 C31 satellite |
图 5给出了BDS-3的C32、C33和C34卫星各个频率的MP序列与高度角关系,MP1~MP5分别代表B1、B2a、B3、B1c和B2b频率,每颗卫星对应频率的三次多项式拟合参数见表 3。

|
图 5 BDS-3 C32、C33和C34卫星MP组合序列与高度角的关系 Fig. 5 The MP series over elevation angles for BDS-3 C32, C33 and C34 satellites |
|
|
表 3 BDS-3 C32、C33和C34卫星的多项式拟合参数 Tab. 3 Cubic polynomial fitting parameters of MP series for BDS-3 C32, C33 and C34 satellites |
由图 5看出,BDS-3卫星5个频率的多路径误差有较明显的差别,尤其是B1和B1c频率,其MP序列的量级明显大于B2a、B2b和B3。对于5个频率,IGSO和MEO卫星均没有明显的与高度角相关的系统偏差。由表 3看出,每颗卫星对应的拟合参数均接近0,B1c频率的A0和A1明显大于其他频率,其原因主要是低高度角时B1c频率的信号受多路径及噪声影响比其他频率更显著,对应MP值的量级较大,甚至可能出现粗差,从而对拟合结果造成偏离。图 5中各卫星的多项式拟合曲线接近0,表明C32、C33和C34卫星的伪距观测值在5个频率上基本不受伪距多路径偏差的影响。
4 结语BDS-2卫星存在与高度角大小相关的伪距多路径偏差,且随高度角的增大逐渐减小。相同类型的卫星对应的伪距多路径偏差基本吻合,MEO卫星的偏差比IGSO卫星的显著。不同频率的偏差有所区别,主要表现为B1频率的偏差大于B2和B3。
BDS-2的C15卫星的MP组合仍存在明显的与高度角相关的系统偏差,经过伪距多路径偏差改正模型改正后基本可以消除。利用实测数据计算BDS-3卫星各个频率的MP组合序列,多项式拟合后系数接近0,表明序列与高度角没有明显的数值关系。BDS-3卫星各频率的伪距观测值基本不受伪距多路径偏差的影响。
| [1] |
Hauschild A, Montenbruck O, Sleewaegen J M, et al. Characterization of Compass M-1 Signals[J]. GPS Solutions, 2012, 16(1): 117-126
(  0) 0) |
| [2] |
Hauschild A, Montenbruck O, Thoelert S, et al. A Multi-Technique Approach for Characterizing the SVN49 Signal Anomaly, Part 1: Receiver Tracking and IQ Constellation[J]. GPS Solutions, 2012, 16(1): 19-28 DOI:10.1007/s10291-011-0203-2
(  0) 0) |
| [3] |
Gisbert J V D, Batzilis N, Risueño G L, et al. GNSS Payload and Signal Characterization Using a 3 m Dish Antenna[C]. ION GNSS, Nashville, 2012
(  0) 0) |
| [4] |
李昕, 曾琪, 管守奎. 北斗卫星伪距多路径偏差改正研究[J]. 大地测量与地球动力学, 2016, 36(8): 727-731 (Li Xin, Zeng Qi, Guan Shoukui. Methods of Beidou Pseudorange Multipath Deviation Correction[J]. Journal of Geodesy and Geodynamics, 2016, 36(8): 727-731)
(  0) 0) |
| [5] |
Wanninger L, Beer S. Beidou Satellite-Induced Code Pseudorange Variations: Diagnosis and Therapy[J]. GPS Solutions, 2015, 19(4): 639-648 DOI:10.1007/s10291-014-0423-3
(  0) 0) |
| [6] |
Xiao W, Liu W X, Sun G F. Modernization Milestone: Beidou M2-S Initial Signal Analysis[J]. GPS Solutions, 2016, 20(1): 125-133 DOI:10.1007/s10291-015-0496-7
(  0) 0) |
| [7] |
Li X, Zhang X H, Pan L. An Improved Method for Eliminating Beidou Satellite Induced Code Bias[C]. EGU General Assembly Conference, Vienna, 2016 http://adsabs.harvard.edu/abs/2016EGUGA..1810984L
(  0) 0) |
| [8] |
张小红, 丁乐乐. 北斗二代观测值质量分析及随机模型精化[J]. 武汉大学学报:信息科学版, 2013, 38(7): 832-835 (Zhang Xiaohong, Ding Lele. Quality Analysis of the Second Generation Compass Observables and Stochastic Model Refining[J]. Geomatics Information Science of Wuhan University, 2013, 38(7): 832-835)
(  0) 0) |
| [9] |
Cazals F, Pouget M. Estimating Differential Quantities Using Polynomial Fitting of Osculating Jets[J]. Computer Aided Geometric Design, 2005, 22(2): 121-146 DOI:10.1016/j.cagd.2004.09.004
(  0) 0) |
| [10] |
Guo F, Li X, Liu W K. Mitigating Beidou Satellite-Induced Code Bias: Taking into Account the Stochastic Model of Corrections[J]. Sensors, 2016, 16(6): 909 DOI:10.3390/s16060909
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38

