2. 西部矿产资源与地质工程教育部重点实验室,西安市雁塔路126号,710054;
3. 地理国情监测国家测绘地理信息局工程技术研究中心,西安市雁塔路126号,710054
近年来,众多学者对GPS多路径误差进行了相关抑制算法、误差特性、影响规律等方面的分析[1-6]。与GPS不同的是,BDS具有3种不同高度的轨道且同时播发3个频点的信号,导致BDS观测值多路径误差可能存在星座间、频点间的差异。目前针对BDS三频多路径特性的研究成果较少,且主要集中在算法及其特性等方面[7-9],而有关误差的差异性研究尚不多见。
本文利用我国的iGMAS跟踪网络和国际MGEX跟踪网络的17个GNSS多模观测站数据,从高度角、信号频点、接收机类型、跟踪站分布以及卫星星座等5个方面进行BDS多路径误差的差异性分析,同时与同源观测站上的GPS观测值多路径误差进行对比,得到了一些有意义的结论。
1 BDS三频多路径误差计算模型采用无几何无电离层组合提取BDS 3个频点的多路径误差,3个频点的多路径误差计算模型分别为[10]:
| $ \begin{array}{l} {\rm{M}}{{\rm{P}}_1} = {P_1}-\left( {1 + \frac{2}{{\alpha {\rm{-}}1}}} \right){L_1} + \left( {\frac{1}{{\alpha-1}}} \right){L_2}\\ = {M_1} + {B_1} - \left( {1 + \frac{2}{{\alpha - 1}}} \right){m_1} + \left( {\frac{2}{{\alpha - 1}}} \right){m_2} \end{array} $ | (1) |
| $ \begin{array}{l} {\rm{M}}{{\rm{P}}_2} = {P_2}-\left( {\frac{{2\alpha }}{{\alpha-1}}} \right){L_1} + \left( {\frac{{2\alpha }}{{\alpha-1}}} \right){L_2}\\ = {M_2} + {B_2} - \left( {\frac{{2\alpha }}{{\alpha - 1}}} \right){m_1} + \left( {\frac{{2\alpha }}{{\alpha - 1}} - 1} \right){m_2} \end{array} $ | (2) |
| $ \begin{array}{l} {\rm{M}}{{\rm{P}}_3} = {P_3}-\left( {\frac{{2\beta }}{{\beta-1}}} \right){L_1} + \left( {\frac{{2\beta }}{{\beta-1}} - 1} \right){L_3}\\ = {M_3} + {B_3} - \left( {\frac{{2\beta }}{{\beta - 1}}} \right){m_1} + \left( {\frac{{2\beta }}{{\beta - 1}} - 1} \right){m_3} \end{array} $ | (3) |
其中,
计算多路径误差时,本文采用移动平均的方法计算伪距的多路径值,即计算出移动窗口内多路径的平均值(一般认为多路径的周期为5~10 min,本文采用的移动窗口宽度为5 min)。具体做法是,对相应时间段内的数据求得移动平均值,再用当前历元的瞬时多路径值减去移动平均值[11]。
计算BDS三频多路径误差的主要流程如图 1所示。

|
图 1 三频多路径误差计算流程 Fig. 1 The calculation process of triple-frequency multipath errors |
选取MGEX和iGMAS的17个跟踪站,采用上述算法计算BDS和GPS的多路径误差,从高度角、信号频点、接收机类型、跟踪站分布以及卫星星座等5个方面进行BDS多路径误差的差异性分析。
2.1 数据来源BDS卫星主要分布在亚太地区,据此选取了2016年第085天MGEX的8个跟踪站(KZN2,JFNG,SEYG,MAYG,CUT0,DUND,NRMG,SIN1)和iGMAS的9个跟踪站(CNYR,GUA1,BJF1,KRCH,KUN1,WHU1,XIA1,THAT,ZHON)的数据,测站分布如表 1所示。
|
|
表 1 测站位置 Tab. 1 Position of stations |
BDS包含3类星座:地球静止轨道卫星GEO(C01、C02、C03、C04、C05)、倾斜地球同步轨道卫星IGSO(C06、C07、C08、C09、C10)、中地球轨道卫星MEO(C11、C12、C13、C14)。为了分析BDS卫星3个频点的多路径效应与高度角之间的相关性,本文以MGEX跟踪网CUT0站为例,随机选取3颗BDS卫星和1颗GPS卫星(C01卫星、C09卫星、C14卫星、G06卫星(MEO)),得到该测站3类卫星的多路径误差与高度角变化的时间序列结果(图 2,图中黄色线为均值)。

|
图 2 不同星座高度角与多路径的时间序列 Fig. 2 Time series of elevation angle and multipath in different constellations |
由于GEO卫星的轨道特性,C01与测站相对位置保持不变,故其高度角趋于稳定变化。C09、C14、G06的多路径误差与高度角相关,当高度角低于30°时,多路径误差与高度角呈负相关;当高度角高于30°时,随着高度角的增大,多路径误差趋于稳定变化。
BDS和GPS卫星的多路径误差与高度角均有较强的相关性。此外,不同频点间BDS的B3(码速率为10 M/s)多路径误差最小,平均优于B1(码速率为2 M/s)和B2(码速率为5 M/s)精度的20 %。说明不同码速率信号的多路径效应表现不同,高码速率的信号频点具有更优的抑制多路径能力。此外,GPS 3个频点中L5多路径误差(MP3)最小,优于L1(MP1)和L2(MP2)的结果;BDS的B3频点优于GPS 3个频点的结果。
2.3 BDS不同星座间的多路径差异分析采用MGEX 8个区域跟踪站BDS三频数据,计算BDS 3类卫星的多路径误差,按高度角分段统计BDS 3类卫星各频点的多路径误差,并引入同源测站上的GPS三频数据进行对比分析,结果如图 3所示。
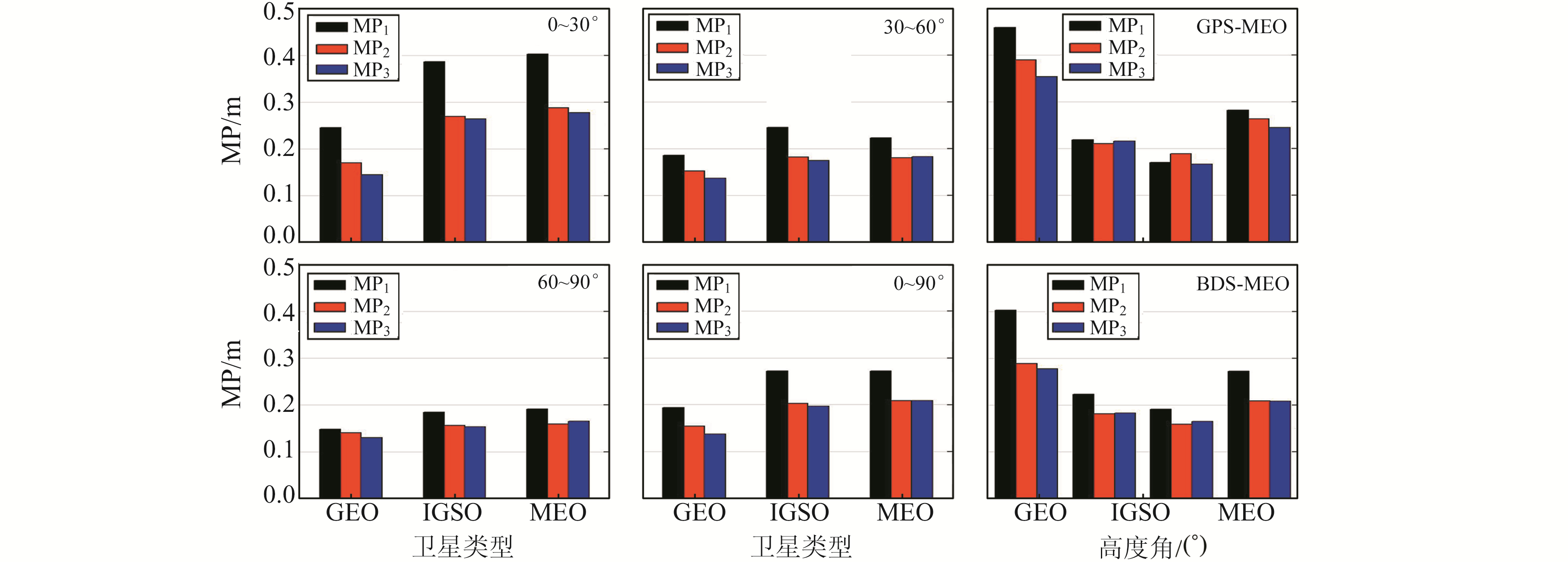
|
图 3 3类卫星的多路径误差 Fig. 3 Multipath errors of three kinds of satellites |
图 3依次给出了高度角为0~30°、30~60°、60~90°和0~90°的BDS 3类卫星以及GPS系统MEO卫星的平均多路径误差值。可以看出,在BDS 3类卫星中,GEO卫星的多路径误差最小,且小于0.25 m,MEO卫星多路径误差最大,但不超过0.4 m。BDS卫星多路径误差的这一特性与卫星的视运动正向有关,因为GEO卫星的运动速度远小于IGSO和MEO卫星,其多路径误差变化频率低。对于不同高度角区间,BDS的MEO卫星的多路径误差结果略优于GPS。
2.4 不同接收机设备的多路径差异性分析为了对比不同接收机的多路径差异,对搭载不同品牌接收机的MGEX和iGMAS站数据进行分析。其中MGEX跟踪站均采用天宝接收机设备,iGMAS跟踪站采用3种国产类型接收机设备。计算这4类接收机BDS和GPS的多路径误差,取各家接收机在同一时段多个跟踪站的多路径误差的平均值,将不同高度角下的多路径误差进行对比分析,4类接收机的多路径结果如图 4所示,其中类型1、类型2、类型3分别为3种不同类型的国产GNSS接收机设备。

|
图 4 不同接收机设备的多路径误差 Fig. 4 Multipath errors of different receivers |
从图 4看出,GPS多路径误差与BDS多路径误差位于同一量级,精度相当。国产接收机类型1的多路径误差最小,优于类型2、3以及天宝接收机结果,不同类型接收机设备的多路径误差存在差异,可能与各厂家设备的抑径能力不同有关。
2.5 不同测站分布下GEO和IGSO卫星的多路径差异鉴于GEO和IGSO卫星的类静地特性,为了对比分析不同测站分布下GEO和IGSO卫星的多路径差异,选取图 1中8个MGEX的跟踪站,分别计算BDS的GEO和IGSO卫星3个频点的多路径误差,按纬度从高到低统计了各测站3个频点的多路径误差,如图 5所示。
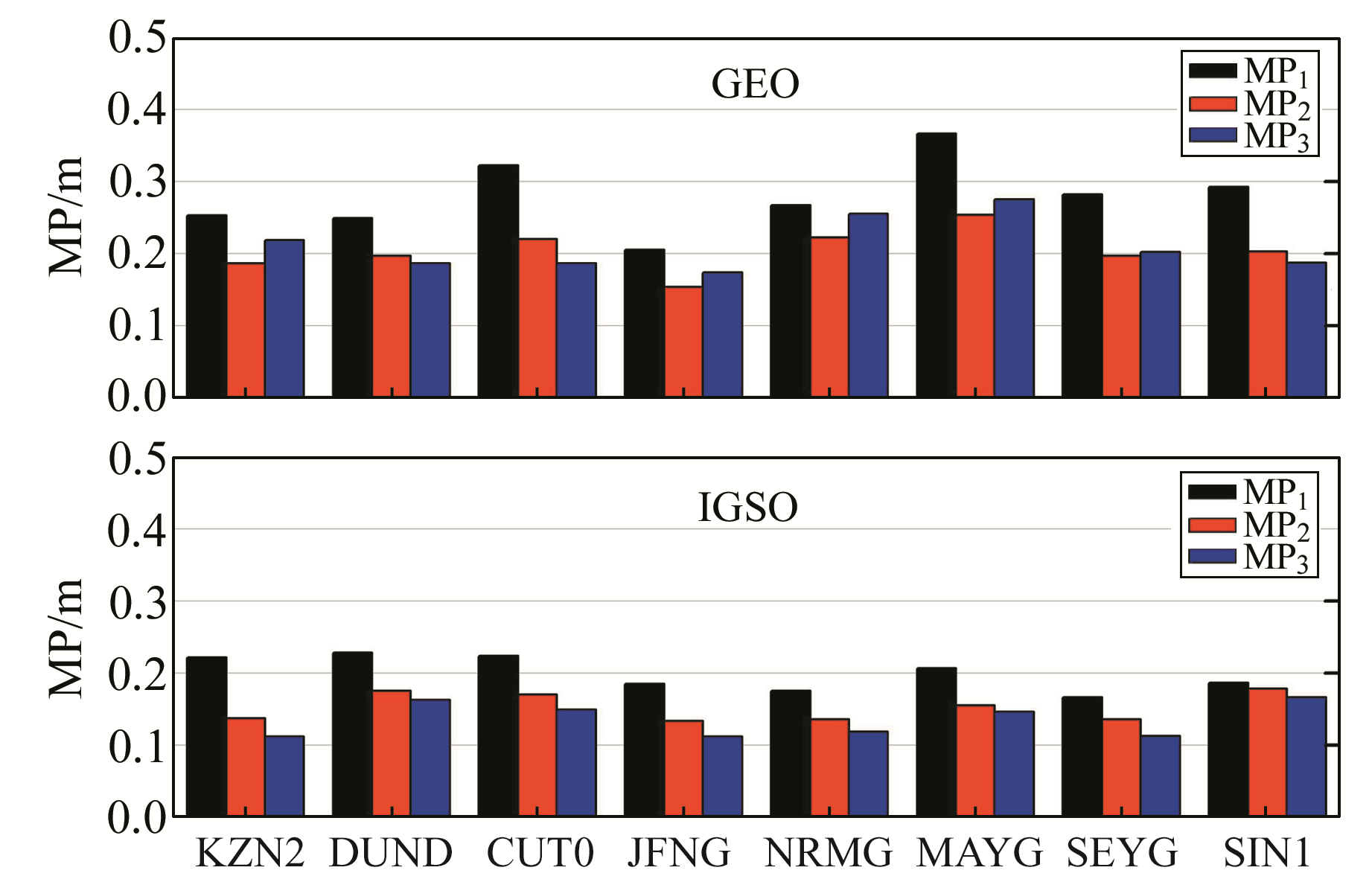
|
图 5 不同区域的多路径误差 Fig. 5 Multipath errors in different regions |
图 5表明,虽然GEO卫星和IGSO卫星各个频点多路径有差异,但同一频点不同测站分布下的多路径误差变化不大,MGEX测站多路径效应整体表现出一致性。因此认为,BDS的GEO和IGSO卫星多路径效应在地域性上无明显相关性,这与MEO卫星多路径效应与地域性无关的结论一致。
3 结语1) BDS和GPS卫星的多路径误差均与高度角有较强的相关性。IGSO和MEO卫星的多路径效应与高度角相关性强,当高度角小于30°时,多路径随高度角增大而减小;当高度角大于30°时,随着高度角增大,多路径误差变化趋于稳定。建议高精度定位时,剔除低高度角数据,以提高数据质量。
2) BDS多路径误差均值为dm级,与GPS多路径效应处于同一量级,BDS不同频点间B3频点的多路径误差最小,平均精度优于B1和B2的20%,且B3频点上的多路径误差优于GPS 3个频点上的对应结果。BDS多路径误差的这一特性与其信号的码速率有关,在实际双频BDS定位和定轨工作中,建议优先选择B3频点进行组合计算。
3) BDS的3类卫星中,GEO卫星的多路径误差最小,优于IGSO卫星和MEO卫星的结果。
4) 3类国产GNSS接收机设备中,类型1的多路径误差最小,优于类型2和3的结果。从多径误差数值来看,类型1接收机设备的多路径指标与国外天宝的多路径指标水平相当。
5) 对于不同纬度的跟踪站,BDS的GEO和IGSO卫星的多路径误差表现出一致性,BDS多路径效应在地域上无明显差异。
| [1] |
夏林元. GPS观测值中的多路径效应理论研究及数值结果[D]. 武汉: 武汉大学, 2001 (Xia Linyuan. Theoretical Study on GPS Observations Multi-Path Effects and Numerical Results[D]. Wuhan : Wuhan University, 2001) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y424660
(  0) 0) |
| [2] |
袁林果, 黄丁发, 丁晓利, 等. GPS载波相位测量中的信号多路径效应影响研究[J]. 测绘学报, 2004, 33(3): 210-215 (Yuan Linguo, Huang Dingfa, Ding Xiaoli, et al. On the Influence of Signal Multipath Effects in GPS Carrier Phase Surveying[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(3): 210-215)
(  0) 0) |
| [3] |
黄声享, 李沛鸿, 杨保岑, 等. GPS动态监测中多路径效应的规律性研究[J]. 武汉大学学报:信息科学版, 2005, 30(10): 870-875 (Huang Shengxiang, Li Peihong, Yang Baocen, et al. Study on the Characteristics of Multipath Effects in GPS Dynamic Deformation Monitoring[J]. Geomatics and Information Science of Wuhan University, 2005, 30(10): 870-875)
(  0) 0) |
| [4] |
郭英起, 黄声享. 高精度GPS定位中多路径影响研究述评[J]. 测绘科学, 2009, 34(3): 66-67 (Guo Yingqi, Huang Shengxiang. A Review of Multipath Effects High Precision GPS Positioning[J]. Science of Surveying and Mapping, 2009, 34(3): 66-67)
(  0) 0) |
| [5] |
Hwang C, Tseng T P, Lin T J, et al. Quality Assessment of FORMOSAT-3/COSMIC and GRACE GPS Observables: Analysis of Multipath, Ionospheric Delay and Phase Residual in Orbit Determination[J]. GPS Solutions, 2010, 14(1): 121-131 DOI:10.1007/s10291-009-0145-0
(  0) 0) |
| [6] |
戴吾蛟, 丁晓利, 朱建军, 等. 基于经验模式分解的滤波去噪法及其在GPS多路径效应中的应用[J]. 测绘学报, 2006, 35(4): 321-327 (Dai Wujiao, Ding Xiaoli, Zhu Jianjun, et al. EMD Filter Method and Its Application in GPS Multipath[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(4): 321-327)
(  0) 0) |
| [7] |
王建军, 马绪瀛. 北斗系统多路径误差特性分析与消除策略[J]. 测绘科学, 2016, 41(1): 18-22 (Wang Jianjun, Ma Xuying. Characteristics Analysis and Elimination Strategies of Multipath Error for BDS[J]. Science of Surveying and Mapping, 2016, 41(1): 18-22)
(  0) 0) |
| [8] |
时荣. 一种计算北斗三频多路径的方法及其结果分析[J]. 测绘与空间地理信息, 2015(8): 175-177 (Shi Rong. A Method for Calculating the Beidou Tri-Band Multipath and Its Result Analysis[J]. Geomatics & Spatial Information, 2015(8): 175-177)
(  0) 0) |
| [9] |
Ma X Y, Shen Y Z. Multipath Error Analysis of COMPASS Triple Frequency Observations[J]. Positioning, 2015(5): 12-21
(  0) 0) |
| [10] |
Wanninger L, Beer S. Beidou Satellite-Induced Code Pseudorange Variations: Diagnosis and Therapy[J]. GPS Solutions, 2015, 19(4): 639-648 DOI:10.1007/s10291-014-0423-3
(  0) 0) |
| [11] |
范士杰, 郭际明, 彭秀英. TEQC在GPS数据预处理中的应用与分析[J]. 测绘信息与工程, 2004, 29(2): 33-35 (Fan Shijie, Guo Jiming, Peng Xiuying. Reasoning about Choosing Representations of Thematic Map[J]. Journal of Geomatics, 2004, 29(2): 33-35)
(  0) 0) |
2. Key Laboratory of Western China's Mineral Resources and Geological Engineering, Ministry of Education, 126 Yanta Road, Xi'an 710054, China;
3. Engineering Research Center of Geographic National Conditions Monitoring, NASMG, 126 Yanta Road, Xi'an 710054, China
 2018, Vol. 38
2018, Vol. 38

