快速高效地完成选星,能够有效满足选星求解的实时性和精度要求[1]。传统的卫星选星法主要包括最小几何精度因子(GDOP)法和最大体积法[2]。最小GDOP法由于其本身的遍历性,将在接收机内部计算Cmn(m为可视星数,n为选星数)次GDOP,从而不可避免地大量使用矩阵相乘和求逆运算,大幅增加计算量的同时也极大地占用了系统资源[3];最大体积法由于涉及的卫星较多,计算量较大且体积不能准确估计,加之耗时较长,使其选星结果不具实时性[1]。为了克服传统算法的缺陷,不少学者提出各自的创新性算法[4-7]。这些方法虽然减少了一定的计算量,但效果不明显,选出的卫星比例仍保持在60%以上,而且这些方法多数只针对单星座系统而言,不能直接应用于多卫星系统融合定位。基于此,本文研究了GNSS选星模型和精密单点定位解算策略,并利用几何二维凸包[8]实现了多系统融合快速选星算法,对选星效果进行分析并利用精密单点定位进行验证。
1 理论基础 1.1 多系统融合PPP的时空基准多卫星系统融合并不是简单地对单卫星系统进行扩展,还必须顾及不同系统的互操作和兼容性问题,这主要体现为不同时间系统和坐标系统的统一及通道的硬件偏差等,目前该问题已经得到有效解决,详细可见文献[9]。其中,BDS、GLONASS、Galileo与GPS的时间系统转换关系可表示为:
| $ \left\{ \begin{array}{l} {t_{{\rm{GPS}}}} = {t_{{\rm{BDS}}}} + t_{{\rm{ISB}}}^{\rm{C}}\\ {t_{{\rm{GPS}}}} = {t_{{\rm{GLONASS}}}} + t_{{\rm{ISB}}}^R\\ {t_{{\rm{GPS}}}} = {t_{{\rm{Galileo}}}} + t_{{\rm{ISB}}}^E \end{array} \right. $ | (1) |
式中,tISBC、tISBR、tISBE分别为BDS、GLONASS、Galileo相对于GPS的系统时间偏差(intersystem-biases,ISB)。在多系统融合PPP中,通常将系统时间偏差作为未知数同坐标、模糊度一起进行参数估计,以此统一时间基准[9]。
1.2 定位精度在GNSS系统中,定位精度可表示为几何精度因子和用户测距误差的乘积[6]。GDOP值在一定的测距误差下表征了定位精度的大小,其反映了由于卫星几何关系的影响造成的伪距测量误差与用户位置误差间的比例系数,是对用户测距误差的放大程度。绝对定位的误差与精度因子DOP值的大小成正比[10]:
| $ {\delta _A} = {\rm{GDOP}} \cdot {\sigma _{{\rm{UERE}}}} $ | (2) |
式中,σUERE为用户测距误差,主要受钟差、测量噪声、对流层误差、电离层误差及多路径效应的影响。其中对定位精度影响最大的是电离层误差,其大小与可视卫星到用户的仰角和方位角密切相关,与系统无关,所以各个系统的单频测距误差的差异较小。为不失一般性,采用和文献[6]中相同的分析方法,假定各个卫星系统的用户测距误差完全相同,则GDOP值的大小便直接表征了定位精度的大小[6]。
考虑到几何精度因子是卫星/用户几何布局的函数,多卫星系统融合的几何精度因子为:
| $ {\rm{GDOP = }}\sqrt {{\rm{trace}}{{\left( {\mathit{\boldsymbol{H}}_{{\rm{mix}}}^{\rm{T}}{\mathit{\boldsymbol{H}}_{{\rm{mix}}}}} \right)}^{-1}}} $ | (3) |
式中,Hmix为GPS/Galileo/GLONASS/BDS组合系统的观测矩阵:
| $ \left[{\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{H'}}}_{{\rm{BDS}}}}}&{{\mathit{\boldsymbol{1}}_{{\rm{BDS}}}}}&{{\mathit{\boldsymbol{0}}_{{\rm{BDS}}}}}&{{\mathit{\boldsymbol{0}}_{{\rm{BDS}}}}}&{{\mathit{\boldsymbol{0}}_{{\rm{BDS}}}}}\\ {{{\mathit{\boldsymbol{H'}}}_{{\rm{GPS}}}}}&{{\mathit{\boldsymbol{0}}_{{\rm{GPS}}}}}&{{\mathit{\boldsymbol{1}}_{{\rm{GPS}}}}}&{{\mathit{\boldsymbol{0}}_{{\rm{GPS}}}}}&{{\mathit{\boldsymbol{0}}_{{\rm{GPS}}}}}\\ {{{\mathit{\boldsymbol{H'}}}_{{\rm{GLONASS}}}}}&{{\mathit{\boldsymbol{0}}_{{\rm{GLONASS}}}}}&{{\mathit{\boldsymbol{0}}_{{\rm{GLONASS}}}}}&{{\mathit{\boldsymbol{1}}_{{\rm{GLONASS}}}}}&{{\mathit{\boldsymbol{0}}_{{\rm{GLONASS}}}}}\\ {{{\mathit{\boldsymbol{H'}}}_{{\rm{Galileo}}}}}&{{\mathit{\boldsymbol{0}}_{{\rm{Galileo}}}}}&{{\mathit{\boldsymbol{0}}_{{\rm{Galileo}}}}}&{{\mathit{\boldsymbol{0}}_{{\rm{Galileo}}}}}&{{\mathit{\boldsymbol{1}}_{{\rm{Galileo}}}}} \end{array}} \right] $ | (4) |
式中,H ′S(S为BDS、GPS、GLONASS、Galileo)为某卫星系统的观测矩阵H的前3列,且H′S为k×3维的矩阵,0S、1S分别表示k×3维的矩阵,k为该系统的可见星数。则H′S的第i列表示为:
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{H'}}}_{{S_i}}} = \left( {\begin{array}{*{20}{c}} {{e_{ix}}}&{{e_{iy}}}&{{e_{iz}}} \end{array}} \right) = }\\ {\left( {\begin{array}{*{20}{c}} {\cos {\rm{E}}{{\rm{L}}_i}\sin {A_i}}&{\cos {\rm{E}}{{\rm{L}}_i}\cos {A_i}}&{\cos {\rm{E}}{{\rm{L}}_i}} \end{array}} \right)} \end{array} $ | (5) |
式中,i=1, 2, …, k为每个系统的可见星编号。
设(xLi, yLi, zLi)为卫星i在当地用户水平坐标系下的三维位置,则该卫星的仰角ELi和方位角Ai表示为:
| $ {\rm{E}}{{\rm{L}}_i} = {\tan ^{-1}}\left( {\frac{{{z_{{L_i}}}}}{{\sqrt {x_{{L_i}}^2 + y_{{L_i}}^2} }}} \right) $ | (6) |
| $ {A_i} = {\tan ^{-1}}\left( {\frac{{{x_{{L_i}}}}}{{{y_{{L_i}}}}}} \right) $ | (7) |
由上述公式可知,多卫星系统融合导航的GDOP值与可见星的仰角和方位角均有关,可通过可见星的空间分布特点快速选出一组构型较优的卫星组合。
1.3 Graham扫描法计算二维凸包在一个实数向量空间V中,对于给定集合X,所有包含X的凸集的交集S定义为X的凸包:
| $ S: = \bigcap\limits_{X \subseteq K \subseteq V} K $ | (8) |
X的凸包可以用X内所有点的线性组合来构造:
| $ S: = \left\{ {\sum\limits_{j = 1}^n {{t_j}{x_j}\left| {{x_j} \in X, } \right.} \sum\limits_{j = 1}^n {{t_j} = 1, {t_j} \in \left[{0, 1} \right]} } \right\} $ | (9) |
本文采用Graham扫描法(Graham’s scan)进行凸包计算。Graham扫描法本质上是运用了“旋转扫除”(rotational sweep)技术,依据点集每个元素对参照极点的极角大小,依次处理[6]。向算法中输入点集Q,调用函数TOP(S),以便在不改变堆栈S的情况下返回处于栈顶的点,并调用函数NEXT-TO-TOP(S)来返回处于堆栈顶部下面的那个点,且不改变堆栈S,即通过设置一个关于候选点的堆栈S来解算凸包。集合Q中的每一个点都会先后被压入堆栈一次,非CH(Q)(表征Q的凸包)中位于顶点的点最终将被弹出堆栈。当算法终止时,堆栈S中仅包含CH(Q)中的顶点,其顺序为各顶点在边界上出现的逆时针方向排列的顺序[7]。
Graham扫描法的具体步骤为(图 1):1)搜索点集Q中最左最低的点并将其设为P0;2)对剩余点按P0的逆时针方向进行排序,将排序后的点记为{P0,P1,P2,…,Pn},如果有多个点有相同的极角,只保留有最大极径的点;3)使P0、P1、P2进入堆栈;4)对k=3~n个点进行如下处理:对NEXT-TO-TOP(S)、TOP(S)和Pk作左转判断,若满足左转要求,则将Pk入栈,k=k+1;若不满足左转要求,则POP(S),k=k-1;5)最终堆栈S中的元素就是凸包的顶点。

|
图 1 Graham扫描法计算凸包的步骤 Fig. 1 Steps of Graham's scan method for calculating convex hull |
本文中动态精密单点定位所涉及的相关设置和处理策略如表 1所示。
2 仿真实验利用MGEX平台获取的多模观测数据对GPS、GLONASS、Galileo和BDS组合系统的选星问题进行仿真,卫星仰角截止角设为5°,仿真时间为24 h,时间间隔为30 s,其中精密单点实验部分采用静态数据动态仿真模式。
单GPS一般只需要通过最大体积法或最小GDOP法挑选4~5颗相对最优星就能完成定位解算。而多系统组合定位时,同一历元中可视卫星将增加到平均35颗左右,由于每加入一个卫星系统便增加一个系统间的钟差参数,最终的状态向量参数将会增加到7维,意味着需要至少选出7颗卫星才能完成定位。加上校验误差所需的另外一颗星[13],本文将选星门限值设为8颗,以确保在每个星历时刻都能实现有效定位解算。
依据负指数衰减模型[6],虽然卫星GDOP值与卫星数目不能构成直接的线性关系,但是总体而言,参与定位解算的卫星数目逐渐减少时,其DOP值也随之增加,所以为了使定位精度不随选星数目减少而损失过度,需对DOP值设定门限值。如表 2所示,DOP的门限值往往由当前使用环境下对定位精度的严格程度决定,通常要求DOP值最大不超过5.0才能作为性能良好的导航卫星,否则其开发潜力不大。由于基于凸包Graham扫描法选出的卫星数目不固定,为了保证定位结果的可靠性,本文将GDOP值的门限值设为2.5,从而确保其定位精度达到优级以上[10]。
|
|
表 2 DOP值与精度的对应关系[10] Tab. 2 Corresponding relationship between DOP values and precision |
图 2是MGEX观测网中5个观测站于2016年DOY=038选星前后卫星数目变化示意图,上半部分为选星前的卫星数目(number≥18),下半部分为选星后的卫星数目(number≤14)。可以看出,选星前的可视卫星数起伏较大,但多数测站在当天的多数历元中的可视卫星仍能保持在30颗以上。而测站POTS因位于BDS的覆盖范围之外,其可视卫星仅在20颗左右。尽管如此,POTS经过最小二维凸包Graham扫描法选出的卫星数目和其他测站一样总能维持在8颗以上,少数历元为7颗,波动范围为9~11颗,完全能够满足四卫星系统组合精密单点定位的解算。相对稳定的选星数目对于减少待求整周模糊度个数有一定意义[14]。

|
图 2 凸包Graham扫描法的选星数目 Fig. 2 The number of selected satellites in the Graham's scan method |
从图 3可以看出,在不同高度角条件下,凸包法的GDOP值总是比最大体积法低。总体而言,随着卫星截止角的增加,两种方法的GDOP值均存在不同程度的起伏。当高度截止角到达25°时,由于接收机所能捕捉的信号大大减少,此时最大体积法的GDOP值已呈现较大波动甚至不能连续,而凸包凭借其算法的可适应性保证了结果的连续性。

|
图 3 凸包法和最大体积法在不同高度截止角的GDOP Fig. 3 The GDOP of convex method and maximum volume method at different elevation angle |
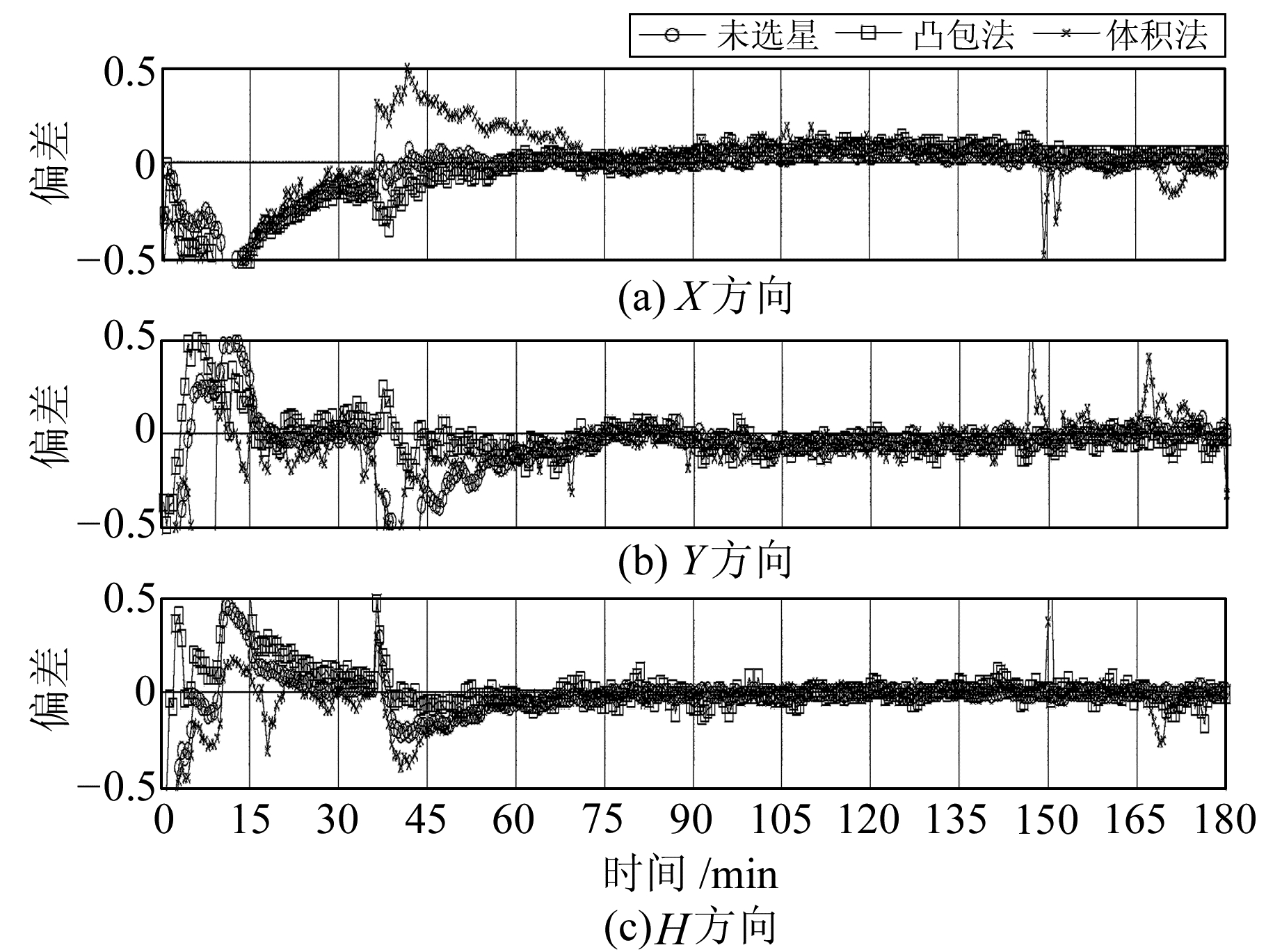
图 4是测站ANMG在未选星、凸包选星、体积法选星3种情况下的动态定位偏差,为便于显示,只给出前3 h的数据,测站的坐标参考值为该站的单天静态解算结果。可以看出,未选星时X、Y、H方向的定位结果收敛时间分别为40 min、60 min、70 min,凸包法选星算法的收敛时间与此相差不大,而体积法选星后收敛时间分别延迟了30 min、15 min、5 min。其后,未选星和凸包法选星的定位偏差已趋于平缓,而体积法仍在部分历元时刻有较大误差,这是由于体积法本身不能准确估计最大体积而导致选星不合理。
|
图 4 3种选星策略下的定位偏差 Fig. 4 Position bias under three kinds of selection algorithms |
从表 3可以看出,凸包选星法的选星数较传统方法略大,其数据处理过程中待估参数和观测方程也更多,但是解算时间却更短。在完全相同的硬件条件和开发平台下,其系统运行时间的优化率可达到36%以上。这进一步说明,凸包选星法能在不损失定位精度的条件下,实现快速简洁地选星,且所选卫星空间构型更优,继而改善PPP定位的收敛速度。
|
|
表 3 3种选星算法的单天数据PPP解算时间对比 Tab. 3 Comparison of single day PPP solution time of three kinds of satellites selection algorithms |
随着空间信息技术的快速发展,如何快速提供实时可靠的高精度导航定位结果成为影响GNSS服务质量的重要因素。为了在多星座观测条件下较大可能地实现定位实时性和精度之间的权衡,基于GDOP值与卫星空间构型体积的关系,本文引入了二维凸包Graham扫描法改进的快速选星法。动态精密单点实验表明,相较传统方法,凸包Graham扫描法能够快速有效地实现优质选星,空间构型明显改善。经本文算法筛选的卫星数目总能维持在8~9颗、10~11颗,选星比例相当于30%、40%,剔除了大量构型不佳的卫星,在不损失精度的前提下能够大幅减少定位解算所消耗的系统运行时间,且使X、Y、H方向的收敛时间分别缩短40%、20%和7%。该选星算法对于保证定位结果的实时性、降低接收机处理器的运算负荷及制造成本具有一定的价值。
本文算法仍有一些待深入研究的细节问题:1)选择合适的判别标准以限定每个历元时刻选取的卫星数目;2)考虑实际应用中不同卫星σUERE的差异对定位结果的影响。
| [1] |
陈灿辉, 张晓林. 一种新的卫星导航系统快速选星方法[J]. 电子学报, 2010, 38(12): 2887-2891 (Chen Canhui, Zhang Xiaolin. A Fast Satellite Selection Approach for Satellite Navigation System[J]. Acta Electronica Sinica, 2010, 38(12): 2887-2891)
(  0) 0) |
| [2] |
汪文雯, 黄彬. 多星座卫星导航系统选星算法的研究[C]. 第五届中国卫星导航学术年会, 南京, 2014 (Wang Wenwen, Huang Bin. Research on Satellite Selection Algorithm for Multi-Satellite Navigation System [C]. The Fifth Annual Conference for Satellite Navigation of China, Nanjing, 2014)
(  0) 0) |
| [3] |
霍航宇, 张晓林. 组合卫星导航系统的快速选星方法[J]. 北京航空航天大学学报, 2015, 41(2): 273-282 (Huo Hangyu, Zhang Xiaolin. Fast Satellite Selection Method for Integrated Navigation Systems[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(2): 273-282)
(  0) 0) |
| [4] |
宋丹, 许承东, 胡春生, 等. 基于遗传算法的多星座选星方法[J]. 宇航学报, 2015, 36(3): 300-308 (Song Dan, Xu Chengdong, Hu Chunsheng, et al. Satellite Selection with Genetic Algorithm under Multi-Constellation[J]. Journal of Astronautics, 2015, 36(3): 300-308)
(  0) 0) |
| [5] |
王兵浩, 吕志伟, 吕金浩. 一种适用于BDS/GPS组合姿态测量的选星算法[J]. 全球定位系统, 2015, 40(4): 41-45 (Wang Binghao, Lü Zhiwei, Lü Jinhao. A Satellite Selection Algorithm in BDS/GPS Combination Attitude Determination[J]. GPS World of China, 2015, 40(4): 41-45)
(  0) 0) |
| [6] |
金玲, 黄智刚, 李锐, 等. 多卫导组合系统的快速选星算法研究[J]. 电子学报, 2009, 37(9): 1931-1936 (Jin Ling, Huang Zhigang, Li Rui, et al. Study on Fast Satellite Selection Algorithm for Integrated Navigation[J]. Acta Electronica Sinica, 2009, 37(9): 1931-1936)
(  0) 0) |
| [7] |
袁社旺, 卓宁. GPS中一种选星方法及实验分析[J]. 中国惯性技术学报, 2008, 16(4): 445-447 (Yuan Shewang, Zhuo Ning. Method of Selecting GPS Satellites and Its Test Analysis[J]. Journal of Chinese Inertial Technology, 2008, 16(4): 445-447)
(  0) 0) |
| [8] |
韩天祥. GNSS多系统选星策略的研究[D]. 上海: 上海交通大学, 2014 (Han Tianxiang. Research on GNSS Multi-System Satellite Selection Strategy[D]. Shanghai: Shanghai Jiaotong University, 2014)
(  0) 0) |
| [9] |
丁赫, 孙付平, 李亚萍, 等. BDS/GPS/GLONASS组合精密单点定位模型及性能分析[J]. 大地测量与地球动力学, 2016, 36(4): 303-307 (Ding He, Sun Fuping, Li Yaping, et al. Modeling and Performance Analysis of Combined BDS/GPS/GLONASS Precise Point Positioning[J]. Journal of Geodesy and Geodynamics, 2016, 36(4): 303-307)
(  0) 0) |
| [10] |
刘慧娟, 党亚民, 王潜心. 多星座实时导航中一种快速次优的选星方法[J]. 测绘科学, 2013, 38(1): 20-22 (Liu Huijuan, Dang Yamin, Wang Qianxin. A Fast Sub-Optimal Satellite Selection Method in Multi-Constellation Real-Time Navigation[J]. Science of Surveying and Mapping, 2013, 38(1): 20-22)
(  0) 0) |
| [11] |
张小红, 左翔, 李盼, 等. BDS/GPS精密单点定位收敛时间与定位精度的比较[J]. 测绘学报, 2015, 44(3): 250-256 (Zhang Xiaohong, Zuo Xiang, Li Pan, et al. Convergence Time and Positioning Accuracy Comparison between BDS and GPS Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(3): 250-256 DOI:10.11947/j.AGCS.2015.20130771)
(  0) 0) |
| [12] |
任晓东, 张柯柯, 李星星, 等. Beidou、Galileo、GLONASS、GPS多系统融合精密单点定位[J]. 测绘学报, 2015, 44(12): 1307-1313 (Ren Xiaodong, Zhang Keke, Li Xingxing, et al. Precise Point Positioning with Multi-Constellation Satellite Systems:Beidou, Galileo, GLONASS, GPS[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(12): 1307-1313)
(  0) 0) |
| [13] |
屈利忠, 赵齐乐, 郭靖, 等. GNSS融合动态精密单点定位性能分析[J]. 大地测量与地球动力学, 2016, 36(4): 298-302 (Qu Lizhong, Zhao Qile, Guo Jing, et al. Performance Analysis on Multi-GNSS Kinematic Precise Point Positioning[J]. Journal of Geodesy and Geodynamics, 2016, 36(4): 298-302)
(  0) 0) |
| [14] |
Roongpiboonsopit D, Karimi A. A Multi-Constellations Satellite Selection Algorithm for Integrated Global Navigation Satellite Systems[J]. Journal of Intelligent Transportation Systems, 2009, 13(3): 127-141 DOI:10.1080/15472450903084238
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38


