传统的PPP模型由于受到卫星和接收机硬件延迟的影响,模糊度不再具有整数特性。为恢复模糊度的整数特性,实现PPP模糊度(PPP-AR)固定解,通常需要加入外在改正产品[1-2]。目前PPP模糊度整数解法常采用消电离层组合,浮点解精度严重影响窄巷模糊度固定,且当前模糊度固定方法多针对单系统。加入GLONASS与BDS观测值,可以显著提高浮点解收敛速度与解算精度,提高窄巷模糊度固定的成功率[3-5]。
本文对多系统组合PPP模糊度固定方法进行研究,介绍多系统融合定位的函数模型,对当前PPP模糊度固定方法进行详细的概述,推导IRC和FCBs产品的转换关系,以CNES提供的IRC产品为例进行实验分析,最后通过GLONASS、BDS辅助GPS模糊度整数解算例进行计算分析。
1 PPP模糊度固定产品分析当前PPP-AR产品包括武汉大学提供的相位偏差小数(FCBs)产品,加拿大自然资源部提供的实时、事后去耦钟(DC)产品以及法国国家太空研究中心(CNES)提供的实时、事后整数钟(IRC)产品。
1.1 去耦钟差产品Collins等[6]提出去耦钟差模型,认为伪距和相位观测值精度不同,在传统的PPP函数模型中,引入含有伪距硬件延迟的卫星钟差,为恢复模糊度的整数特性,应将卫星的伪距钟差和相位钟差区别对待。在去耦钟差模型中,伪距和相位对应的卫星钟差分别单独估计,使得模糊度不受伪距硬件延迟的影响,从而恢复模糊度的整数特性。去耦钟差模型通过构造伪距和相位的无电离层组合(IF)观测值,联合MW宽巷组合解算模糊度。其函数模型为[7]:
| $ \left\{ \begin{array}{l} {P_{{\rm{IF}}}} = \rho + (c{\rm{d}}t_{{P_{{\rm{IF}}}}}^r-c{\rm{d}}t_{{P_{{\rm{IF}}}}}^s) + T + {\varepsilon _{{P_{{\rm{IF}}}}}}\\ {L_{{\rm{IF}}}} = \rho + (c{\rm{d}}t_{{L_{{\rm{IF}}}}}^r-c{\rm{d}}t_{{L_{{\rm{IF}}}}}^s) + \\ \;\;\;T-{\lambda _{{\rm{IF}}}}(17{N_1} + 60{N_{{\rm{WL}}}}) + {\varepsilon _{{L_{{\rm{IF}}}}}}\\ {A_{{\rm{MW}}}} = (b_{{A_{{\rm{MW}}}}}^r - b_{{A_{{\rm{MW}}}}}^s) - {N_{{\rm{WL}}}} + {\varepsilon _{{A_{{\rm{MW}}}}}} \end{array} \right. $ | (1) |
式中,P为伪距观测值,L为载波相位观测值,ρ为测站与卫星之间几何距离,c为光速,dtr、dts分别为接收机、卫星钟差,T为对流层延迟,ε为观测噪声,N为模糊度,A为模糊度解,b为小数偏差值。其中,(cdtsPIF, cdtsLIF, bsAMW)和(cdtrPIF, cdtrLIF, brAMW)分别称为卫星和接收机的去耦钟差参数。在组网解算去耦钟差参数时,由于未知参数个数比观测方程个数多,导致观测方程出现秩亏,为求解去耦钟差参数,通常需要设置强约束或者基准。用户接收到卫星的去耦钟差参数后,将参数回代到式(1)中,此时为了消除观测方程秩亏,使未知参数有解,需要设置模糊度参考基准。利用式(1)可以直接解算出模糊度的宽巷NNW和N1的整数解,从而实现PPP的模糊度固定。
1.2 整数钟产品与去耦钟模型相似,IRC[8]同样是对伪距钟和相位钟分别估计从而恢复模糊度的整数特性。二者区别在于宽巷模糊度NNW和窄巷模糊度N1的求解不同,整数钟是通过弧段平滑取平均固定宽巷模糊度NNW,然后将NNW代入PPP函数模型中求解N1值,其函数模型为[9]:
| $ {A_{{\rm{MW}}}} = (b_{{A_{{\rm{MW}}}}}^r-b_{{A_{{\rm{MW}}}}}^s)-{N_{{\rm{WL}}}} + {\varepsilon _{{A_{{\rm{MW}}}}}} $ | (2) |
| $ \left\{ \begin{array}{l} {P_{{\rm{IF}}}} = \rho + (c{\rm{d}}t_{{P_{{\rm{IF}}}}}^r-c{\rm{d}}t_{{P_{{\rm{IF}}}}}^s) + T + {\varepsilon _{{P_{{\rm{IF}}}}}}\\ {L_{{\rm{IF}}}} = \rho + (c{\rm{d}}t_{{L_{{\rm{IF}}}}}^r-c{\rm{d}}t_{{L_{{\rm{IF}}}}}^s) + \\ \;\;\;\;T-{\lambda _{{\rm{IF}}}}(17{N_1} + 60{N_{{\rm{WL}}}}) + {\varepsilon _{{L_{{\rm{IF}}}}}} \end{array} \right. $ | (3) |
式中,(cdtsPIF, cdtsLIF, bsAMW)为整数钟函数模型的参数。该参数与去耦钟差参数类似,只是在参数的解算中,基准的选取和解算步骤不同,其中cdtsPIF可以通过IGS获得。整数钟参数的估计通常先估计宽巷小数偏差bsAMW,然后回代式(3)中固定宽巷模糊度NWL,最后求解cdtsLIF。
对于用户端而言,接收到整数钟产品(cdtsPIF, cdtsLIF, bsAMW)后,首先,利用式(4)求卫星的宽巷小数偏差对宽巷模糊度进行改正,利用式(5)计算多颗卫星平均值获得接收机端小数偏差,将接收机和卫星端的小数偏差代入式(6)获得宽巷模糊度的整数解;然后,将获得的宽巷整数解NWL代入式(3)的相位观测值,求解窄巷模糊度N1,并利用LAMBDA方法[10]对其进行搜索固定。
| $ {A_{{\rm{MW}}}} = b_{{A_{{\rm{MW}}}}}^s-{N_{{\rm{WL}}}} + b_{{A_{{\rm{MW}}}}}^r $ | (4) |
| $ \bar b_{{A_{{\rm{MW}}}}}^r = \frac{1}{n}\sum\limits_{i = 1}^n {{\rm{frac}}} {\left( {{A_{{\rm{MW}}}} + b_{{A_{{\rm{MW}}}}}^s} \right)_i} $ | (5) |
| $ \begin{array}{l} {L_{{\rm{IF}}}}-60{\lambda _{{\rm{IF}}}}{N_{{\rm{WL}}}} = \rho + (c{\rm{d}}t_{{L_{{\rm{IF}}}}}^r-c{\rm{d}}t_{{L_{{\rm{IF}}}}}^s) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;T-{\lambda _{{\rm{IF}}}}17{N_1} + {\varepsilon _{{L_{{\rm{IF}}}}}} \end{array} $ | (6) |
李星星等[11]深入分析了PPP模糊度不具有整数特性的原因,并根据当前用户多采用IGS提供的星历和钟差产品,提出了非差模糊度固定方法,即模糊度小数偏差法。其利用IGS跟踪网的观测数据求解卫星端的相位小数偏差,用户利用这些小数偏差可以恢复模糊度的整数特性,从而实现PPP模糊度固定解。该方法根据宽巷模糊度具有长波长的特性,先固定宽巷模糊度NWL,然后利用已固定的宽巷模糊度与无电离层组合模糊度NIF求解窄巷模糊度的实数解,再固定窄巷模糊度N1,最后得到模糊度固定的PPP解。
用户端利用服务端播发的产品bsAMW和bs,改正宽巷模糊度和窄巷模糊度的卫星端小数偏差,再根据式(5)获得接收机端的小数偏差,以恢复模糊度的整数特性,从而实现PPP的整数解。
1.4 产品之间的转换关系不同的PPP-AR产品都包含了相同的信息,因此可以相互转换。通过产品相互转换,用户可以检验不同产品的精度和准确度。使用不同的产品进行PPP解算,可以提高解算结果的可靠性。由于IRC和DC产品是相同的,只是在解算步骤上对宽巷模糊度的解算策略不同,因此,这里只给出IRC和FCBs产品的相互转换关系。FCBs的产品包括(dtsPIF, bsAMW, b1s),其中dtsPIF是IGS提供的钟差产品。FCBs产品与IRC产品的差别在于窄巷硬件延迟的估计,IRC方法是将窄巷硬件延迟吸收到相位钟差中,而FCBs则是对其进行估计。在宽巷硬件延迟的解算上,两种产品的计算方法是一样的,都是假定宽巷硬件延迟比较平稳,在一个弧段内是一个常数。在这两个产品的计算中,为解除计算产品时的秩亏问题,都采用相同的处理方法。两种产品的转换关系为:
| $ \left[\begin{array}{l} {\rm{d}}t_{{P_{{\rm{IF}}}}}^s\\ {\rm{d}}t_{{L_{{\rm{IF}}}}}^s\\ b_{{A_{{\rm{MW}}}}}^s \end{array} \right] = \left[{\begin{array}{*{20}{c}} 1&0&0\\ 1&{-\frac{c}{{{f_1} + {f_2}}}}&{-\frac{{c{f_2}}}{{f_1^2-f_2^2}}}\\ 0&0&1 \end{array}} \right]\left[\begin{array}{l} {\rm{d}}t_{{P_{{\rm{IF}}}}}^s\\ b_1^s\\ b_{{A_{{\rm{MW}}}}}^s \end{array} \right] $ | (7) |
CNES是IGS的一个运行数据中心,可以为用户提供实时和事后的IRC产品以及卫星的轨道产品。本文以CNES提供的产品为例进行分析。
图 1为2015-01-01~2016-03-05的GPS卫星端宽巷偏差(WSB)。可以看出,大部分卫星WSB短期、长期均变化平稳,只有少数卫星的变化相对剧烈。由于WSB与卫星钟有关,因此卫星钟的老化会对其有很大的影响。宽巷偏差在48 h内是一个比较稳定的常数,CNES所提供的产品的变化趋势与Ge等[1]的结论一致。

|
图 1 CNES宽巷小数偏差 Fig. 1 Wide lane satellite bias(GPS) |
图 2为2015-05-04 IGS G01卫星码钟差和CNES G01卫星相位钟差的对比。可以看出,IGS的码钟差在时段内会发生周期性的跳变,在一个周期内保持为常数,这是因为解算码钟差时通常将码偏差约束为常数,而实际上码偏差是随着时间变化的,使得IGS码钟差发生跳变;CNES的相位钟差则是随着时间发生变化,码偏差对相位钟差解算没有影响,而相位钟差也受到相位硬件延迟的影响,所以在时域上缓慢变化;IGS的钟差和CNES的相位钟差存在明显的系统性偏差,这与码偏差对伪距和相位的影响以及相位观测值的精度远高于码观测值的精度有关。

|
图 2 CNES相位钟差与IGS的码钟差 Fig. 2 Phase clock bias of CNES and code clock bias of IGS |
图 3给出了2015-05-04 CNES G01卫星与IGS G01卫星轨道的三维坐标。可以看出,CNES的卫星轨道与IGS的卫星轨道具有高度吻合性,这是CNES的IRC产品实现PPP模糊度固定的关键,也是实现高精度定位的关键。
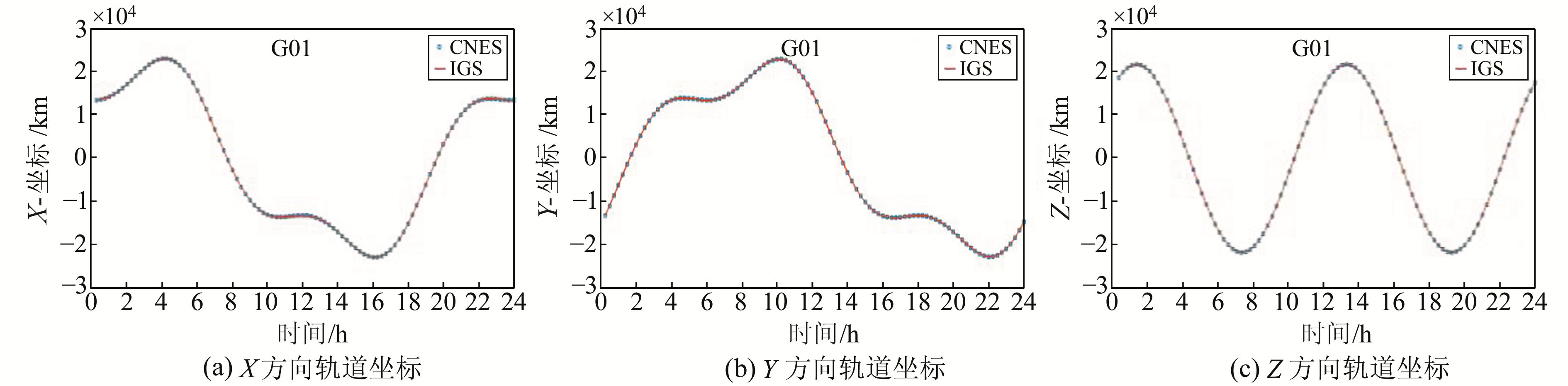
|
图 3 CNES和IGS的轨道坐标序列 Fig. 3 Orbital coordinate sequence of CNES and IGS |
为了验证IRC产品可以实现模糊度固定,以及多系统组合可以加快PPP收敛时间和初始固定的精度,设计单系统、双系统和三系统PPP模糊度固定的对比实验。
采用2015-05-04的15个MGEX跟踪站静态观测数据,采样间隔为30 s,PPP固定解使用的卫星轨道和钟差产品为CNES的事后精密星历和钟差。采用单系统(GPS,G)、双系统(GPS+BDS,GB;GPS+GLONASS,GR)和三系统(GPS+BDS+GLONASS,GBR)4种模式分析比较其模糊度初始固定时所用的时间和定位性能。
图 4给出了CUT0测站4种模式的可用卫星数。可以看出,GPS单系统可用卫星数基本少于10颗,观测条件较差时仅有6颗可用卫星;双系统(GB,GR)模式的可用卫星数基本维持在15颗左右,是单系统的2~3倍;三系统的可用卫星数大于20颗,是单系统的3~4倍。
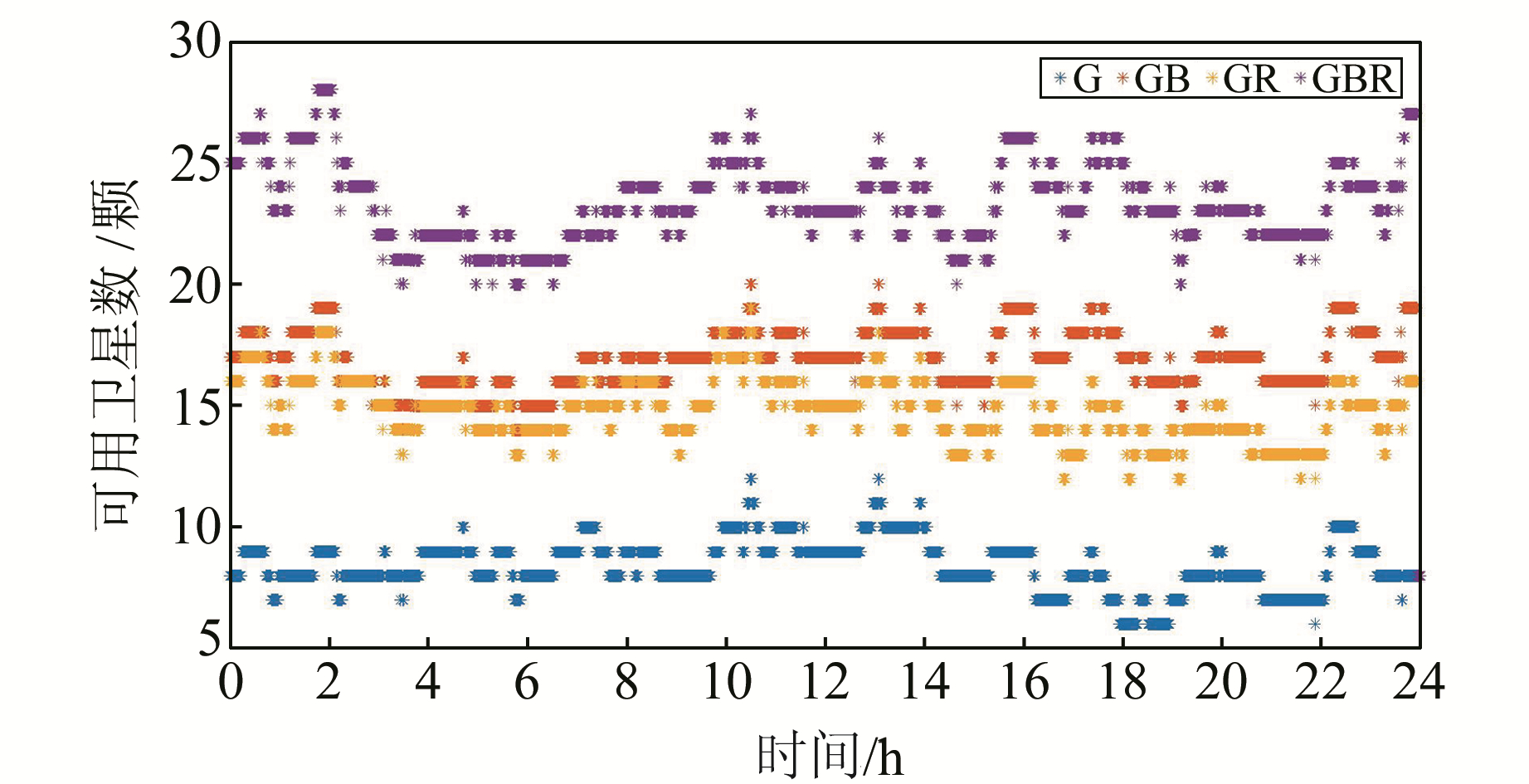
|
图 4 CUT0测站的可用卫星数 Fig. 4 Number of available satellites of CUT0 station |
图 5给出了CUT0测站4种模式的PDOP值统计。PDOP值反映的是卫星几何强度,其值越小,卫星几何强度越大。可以看出,GBR模式的PDOP值最小,基本维持在1.1左右;G模式的PDOP值最大,最大可达4.4。结合图 4可以看出,PDOP值的大小与可用卫星数相关。
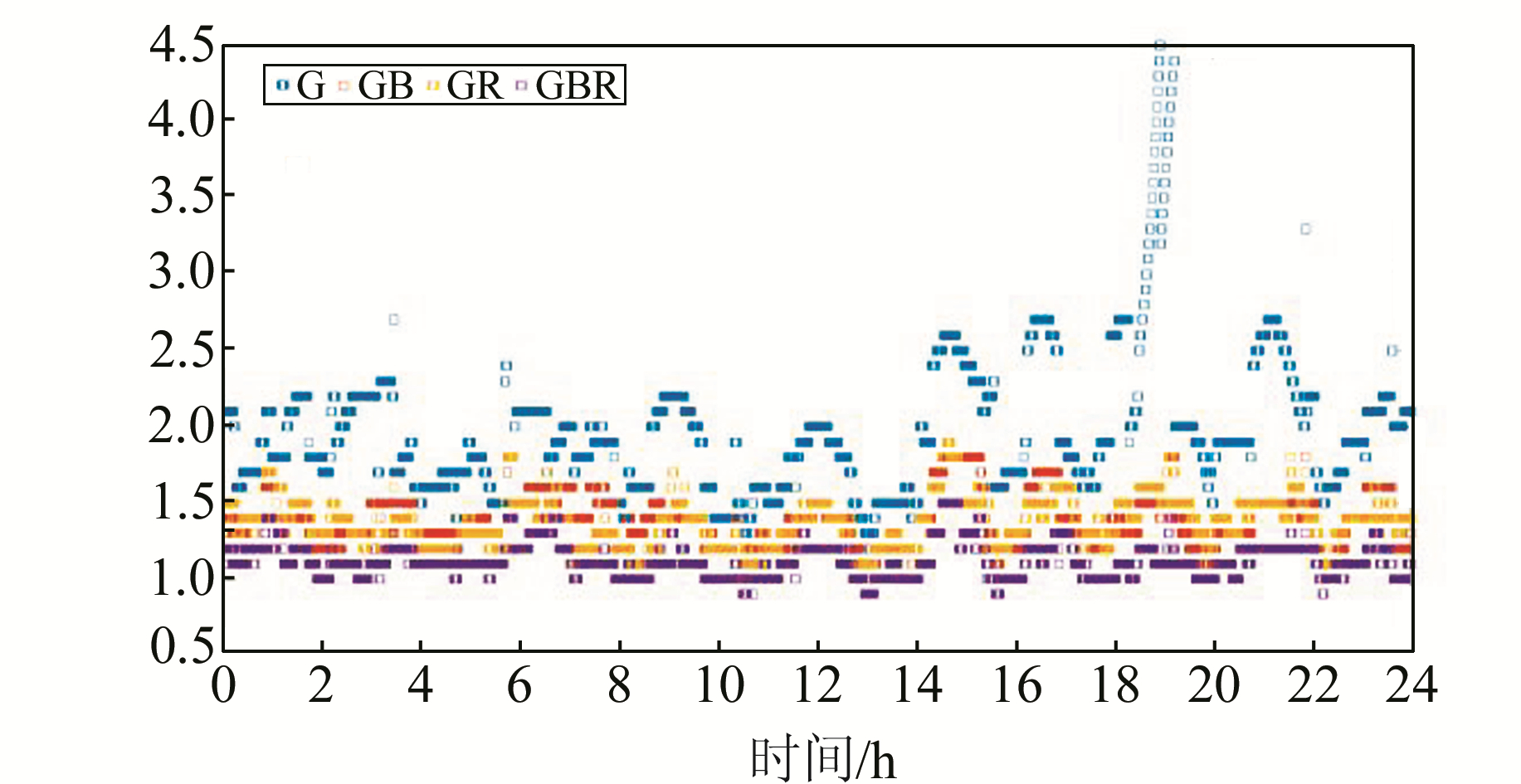
|
图 5 CUT0测站PDOP值 Fig. 5 PDOP values of CUT0 station |
图 6给出了CUT0测站的卫星天空图。可以看到,多系统融合的可观测卫星数明显增多,且空间的几何结构更强。

|
图 6 CUT0测站的天空图 Fig. 6 Sky map of CUT0 station |
图 7给出了DUND测站4种模式的静态PPP前120个历元的定位偏差。可以看出,未固定模糊度前,在精度和收敛时间上GB相对较差,GBR次之,GR最好。这与BDS系统有关,因为GEO卫星轨道精度较差,且BDS卫星的天线相位中心偏差和变化依然采用初始标定值,这与其真实值间存在一定的偏差,使得加入BDS系统后精度和收敛时间都差于其他模式。从图中东方向分量可以看出,模糊度固定后,定位偏差有明显的改善。三系统组合时,模糊度初始固定的时间最短,单系统初始固定的时间最长,双系统组合介于二者之间。

|
图 7 DUND测站的PPP固定解 Fig. 7 PPP fixed solution of DUND station |
图 8和图 9分别给出了4种定位模式模糊度初始固定的时间和定位偏差。从图 8可以看出,多系统的融合可以加快模糊度固定,单系统模糊度固定一般需要30 min左右,而三系统和双系统只需20 min左右。从图 9可以看出,多系统定位模糊度首次固定时,其定位偏差要小于单系统,并且随着卫星数的增加定位偏差逐渐减小。

|
图 8 模糊度初始固定的时间 Fig. 8 Frist fixed-time of ambiguity |

|
图 9 初始固定时的定位精度 Fig. 9 Positioning accuracy of frist fixed |
表 1为15个测站模糊度首次固定时的平均定位偏差和模糊度的平均固定时间统计结果。可以看到,模糊度固定后水平方向可以实现1~2 cm的定位偏差,高程方向可以实现5 cm的定位偏差;多系统融合定位时,定位精度有明显提高,GBR模式相比于G模式, E方向上精度提高了54.4%,N方向提高了7.4%,U方向提高了59.9%;在平均固定模糊度的时间上,单系统需要32.7 min,而三系统只需要21.0 min,时间缩短了35.6%。
|
|
表 1 15个测站的平均定位偏差及固定时间 Tab. 1 Average positioning bias and fixed-time of 15 stations |
综上所述,当多系统融合定位时,加入BDS系统会使得PPP的浮点解变差。多系统融合时可用卫星数越多,PDOP值越小,空间几何结构越强,可以加快模糊度固定的时间,提高模糊度初始固定时的定位精度。
4 结语1) IRC产品中的WSB在一定时间内稳定为一常数,相位钟差与IGS的码钟差具有明显的系统跳跃,卫星轨道与IGS轨道相同。
2) 无论是静态还是动态,CENS提供的事后IRC产品都可以使得PPP模糊度恢复整数特性,并且可以实现PPP模糊度的固定解。PPP模糊度固定解可以缩短PPP的收敛时间,提高PPP的定位精度。
3) 当多系统融合定位时,加入BDS系统会使得PPP的浮点解变差;多系统融合时可用卫星数增多,PDOP值减小,空间几何结构变强。这不仅可以加快模糊度固定的时间,同时也可以提高模糊度初始固定时的定位精度。
| [1] |
Ge M, Gendt G, Rothacher M, et al. Resolution of GPS Carrier-Phase Ambiguities in Precise Point Positioning (PPP) with Daily Observations[J]. International Journal of Implant Dentistry, 2008, 82(7): 389-399
(  0) 0) |
| [2] |
Geng J H, Meng X L, Dodson A H, et al. Integer Ambiguity Resolution in Precise Point Positioning: Method Comparison[J]. Journal of Geodesy, 2010, 84(9): 569-581 DOI:10.1007/s00190-010-0399-x
(  0) 0) |
| [3] |
Jokinen A, Feng S J, Schuster W, et al. GLONASS Aided GPS Ambiguity Fixed Precise Point Positioning[J]. Journal of Navigation, 2013, 66(3): 399-416 DOI:10.1017/S0373463313000052
(  0) 0) |
| [4] |
Li P, Zhang X H. Integrating GPS and GLONASS to Accelerate Convergence and Initialization Times of Precise Point Positioning[J]. GPS Solutions, 2014, 18(3): 461-471 DOI:10.1007/s10291-013-0345-5
(  0) 0) |
| [5] |
蔡昌盛. GPS/GLONASS组合精密单点定位理论与方法[D]. 徐州: 中国矿业大学, 2008 (Cai Changsheng. Theory and Method of Combined GPS/GLONASS Precise Point Positioning[D]. Xuzhou: China University of Mining, 2008) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=chtb201407002
(  0) 0) |
| [6] |
Collins P, Bisnath S, Lahaye F, et al. Undifferenced GPS Ambiguity Resolution Using the Decoupled Clock Model and Ambiguity Datum Fixing[J]. Navigation, 2010, 57(2): 123-135 DOI:10.1002/navi.2010.57.issue-2
(  0) 0) |
| [7] |
Shi J B, Gao Y. A Comparison of Three PPP Integer Ambiguity Resolution Methods[J]. GPS Solutions, 2014, 18(4): 519-528 DOI:10.1007/s10291-013-0348-2
(  0) 0) |
| [8] |
Laurichesse D, Mercier F, Berthias J P, et al. Integer Ambiguity Resolution on Undifferenced GPS Phase Measurements and Its Application to PPP and Satellite Precise Orbit Determination[J]. Navigation, 2009, 56(2): 135-149 DOI:10.1002/navi.2009.56.issue-2
(  0) 0) |
| [9] |
Loyer S, Perosanz F, Mercier F, et al. Zero-Difference GPS Ambiguity Resolution at CNES-CLS IGS Analysis Center[J]. Journal of Geodesy, 2012, 86(11): 991-1 DOI:10.1007/s00190-012-0559-2
(  0) 0) |
| [10] |
Teunissen P J L. The Least Squares Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy, 1995, 70(1-2): 65-82 DOI:10.1007/BF00863419
(  0) 0) |
| [11] |
李星星. GNSS精密单点定位及非差模糊度快速确定方法研究[D]. 武汉: 武汉大学, 2013 (Li Xingxing. Rapid Ambiguity Resolution in GNSS Precise Point Positioning[D]. Wuhan: Wuhan University, 2013) http://cdmd.cnki.com.cn/Article/CDMD-10486-1014135460.htm
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38

