2. 中国科学院大学地球科学学院, 北京市玉泉路19号(甲), 100049
大地震除产生涉及地球局部运动的体波和面波外,还能激发全球规模、维持数天的地球自由振荡。地球自由振荡是地震面波在传播过程中形成的驻波,其能量大小与震源破裂方式和破裂程度密切相关[1]。地球自由振荡存在环型振荡nTlm和球型振荡nSlm两种基本振型,其中n为沿半径方向零位移面的数目,l和m分别为纬度和经度方向的阶数[2-3],可被用于研究地球的内部结构[4]。开展中国大陆中部地区上地幔介质横向特性的研究,不仅可以更精细地认识上地幔的性质,且对研究该区地震发生的深部构造环境、探讨地震孕育、发生规律及预测均具有重要价值,对矿产资源预测也能提供一定的帮助[5]。
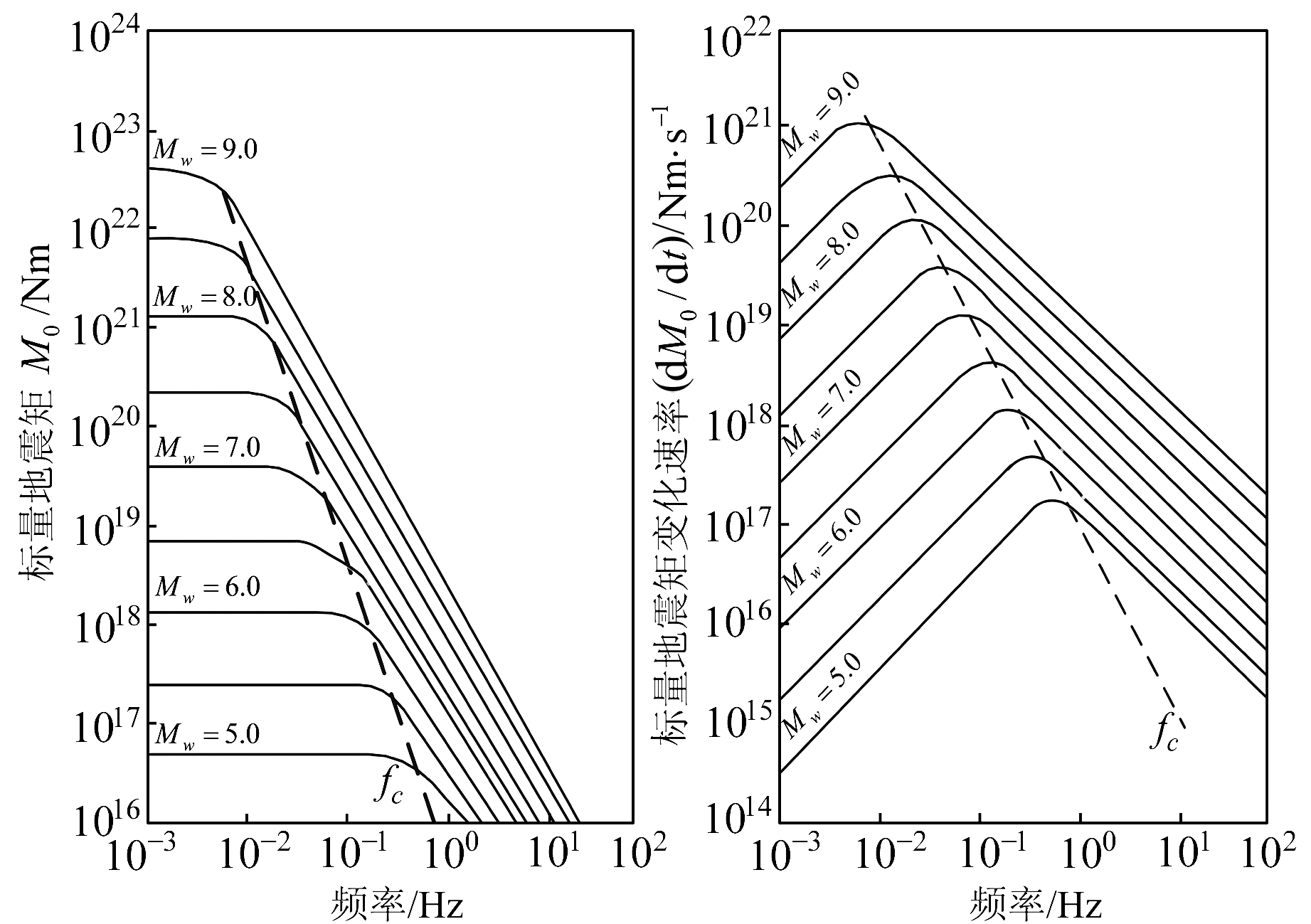
根据Aki[6]的研究,地震矩在一定的频率范围与地震引起的位移成正比(图 1)。大地震较低的转角频率fc会使地震矩在较高的频段快速衰减,导致地震矩与位移成正比的频率范围较狭窄,不便于在较宽的频带范围利用简正模研究上地幔的介质横向特性。Xu等[7]以2013年芦山地震为研究对象,利用中国大陆附近的17个台站的简振模观测值研究横向不均匀性,证明了利用简振模研究上地幔横向不均匀性的可行性。本文选用中国大陆附近发生的中级地震为研究对象,以大陆中部的3个地震台和2个超导台站记录的球型简振模,研究台站覆盖区域上地幔的介质横向特性。
|
图 1 地震矩频率范围与位移振幅 Fig. 1 Seismic moment is proportional to the displacement amplitude |
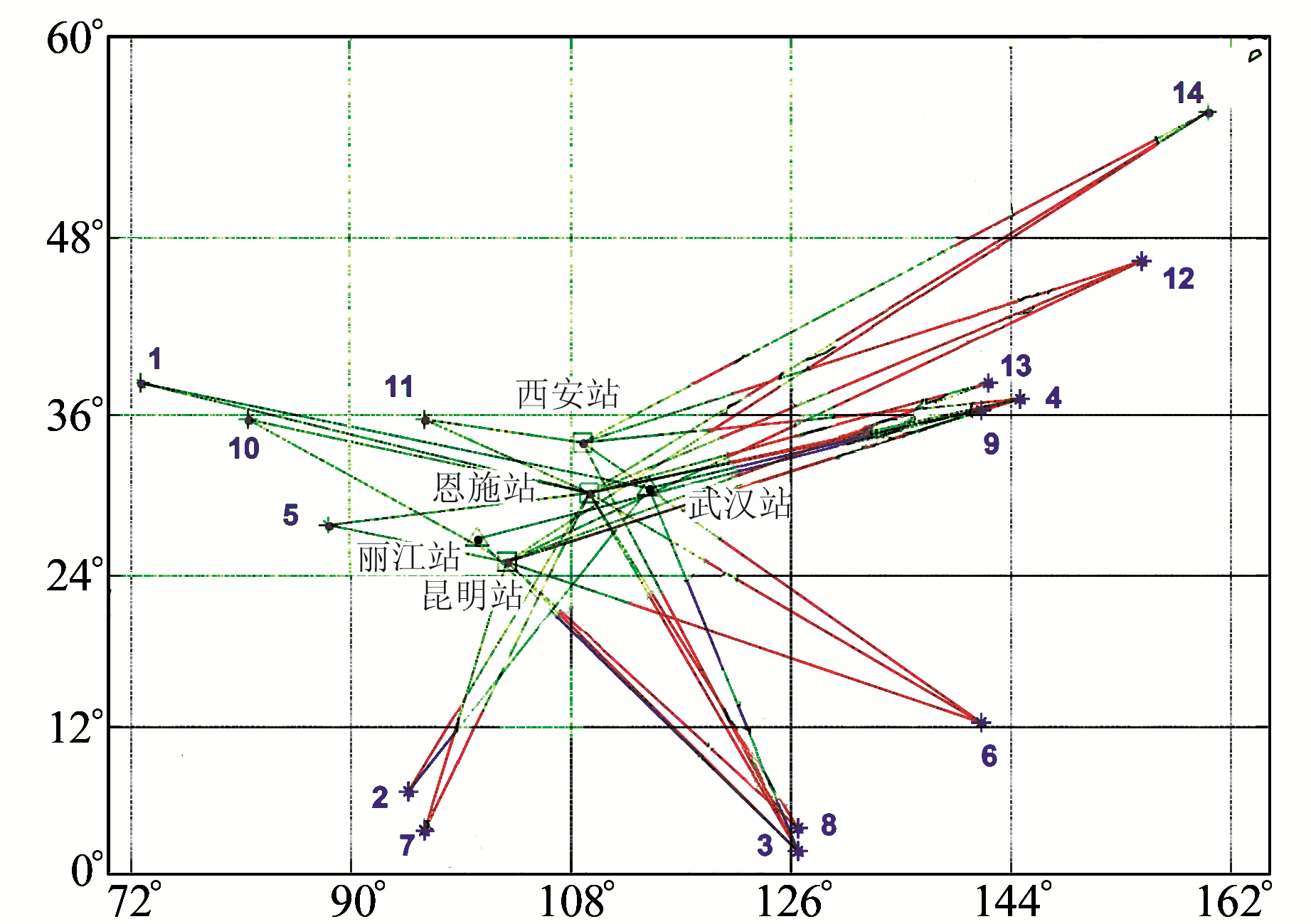
选取2004~2015年发生在我国大陆附近的矩震级为6.5~7.5的14个地震事件,参数见表 1,震源及台站分布见图 2。考虑到大陆中部地区台站分布、台站数据的优劣、台站和地震震中连线的分布以及能够提供低频LHZ数据的台站情况,选用安装STS-1宽频带地震仪的恩施、昆明和西安地震台观测值为原始数据。由于宽频带地震仪水平记录值噪音太大导致谱变换之后很难测定简振模的谱峰[7],所以主要分析LHZ数据。
|
|
表 1 地震事件及相关参数 Tab. 1 Earthquake events and related parameters |
|
图 2 地震震源、3个地震台和2个超导台的位置 Fig. 2 The locations of seismic epicenters, three seismic stations and two superconducting stations |
宽频带地震仪将地面的振动信号转化为电信号,但两者间转化系数随振动振幅和频率变化,因此宽频带地震仪去仪器响应后低频观测数据可能会出现标定问题[8]。超导重力仪用磁悬浮超导球的位置变化记录重力的变化,其响应特性可以用一个标定格值因子描述,该量通过超导重力仪和绝对重力仪同时观测地球潮汐参数的比较得到[9-11]。此外,超导重力仪具有很高的灵敏度和稳定性、较低的噪音水平和漂移、很宽的动态频率响应范围,可以检测周期从数s到几a的重力场信号,准确地记录低频地球自由振荡信号[11]。在100 s周期内,超导重力仪转化函数稳定平滑,且标定格值因子为常值,在记录周期100 s以上的简振模时不会出现标定格值因子的问题[7]。因此,文中用位置相同或相近的地震仪和超导重力仪的简振模观测值进行对比,由两者的拟合程度说明宽频带地震仪记录的有效性,以此来约束宽频带地震仪的标定问题。
1.2 简振模观测值与模拟值对3个地震台和2个超导重力仪观测值进行傅里叶谱变换,在频域比较简振模观测值和模拟值振幅差异,以此判断上地幔深部区域是否存在大范围横向不均匀结构。经数据筛选和预处理后,每个台站数据如下:恩施台13个,昆明台11个,西安台6个,丽江台2个,武汉台4个。
根据矩张量和横向均匀地球参考模型,可以计算测站r0处由点源地震激发的简振模位移。当点源处的时间函数是一阶跃函数时,在r处的位移u(r, t)为[12]:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{u}}\left({\mathit{\boldsymbol{r}}, t} \right) = \sum\limits_{n = 1} {\frac{{1-\cos {\omega _n}t \cdot \exp \left({-{\omega _n}t/2{Q_n}} \right)}}{{\omega _n^2}} \cdot } }\\ {{\mathit{\boldsymbol{S}}_n}\left(\mathit{\boldsymbol{r}} \right)\; \cdot \;\left({\mathit{\boldsymbol{M}}\left({{\mathit{\boldsymbol{r}}_0}} \right)\; \cdot \;{\mathit{\boldsymbol{\varepsilon }}_n}\left({{\mathit{\boldsymbol{r}}_0}} \right)} \right)} \end{array} $ | (1) |
式中,Sn(r)为测站上n阶简振模归一化的本征位移,ωn为本征频率,Qn为品质因子,εn(r)为点源在Sn(r)处的应变张量,M(r0)为点源的矩张量。
定义
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\alpha }}_k}\left( {\mathit{\boldsymbol{r}}, t} \right) = }\\ {\sum\limits_n {\frac{{1-\cos {\omega _n}t \cdot \exp \left( {-{\omega _n}t/2{Q_n}} \right)}}{{\omega _n^2}} \cdot {\mathit{\boldsymbol{S}}_n}\left( \mathit{\boldsymbol{r}} \right)\; \cdot \;{\mathit{\boldsymbol{\varepsilon }}_{nk}}} } \end{array} $ | (2) |
式中,εnk为εn(r0)的分量,则式(1)变为:
| $ {\mathit{\boldsymbol{u}}_v}\left( {\mathit{\boldsymbol{r}}, t} \right) = \sum\limits_{k = 1}^6 {{\mathit{\boldsymbol{\alpha }}_k}\left( {\mathit{\boldsymbol{r}}, t} \right){\mathit{\boldsymbol{M}}_k}} $ | (3) |
式中,αk(r, t)为传递函数,可由一维地球模型计算得到,对称矩张量Mk可由地震震源机制解得到[13]:
| $ \begin{array}{l} {M_1} =-{M_0}({\rm{sin}}\delta {\rm{cos}}\lambda {\rm{sin}}2\varphi + {\rm{sin}}2\delta {\rm{sin}}\lambda {\rm{si}}{{\rm{n}}^2}\varphi )\\ {M_2} = {M_0}({\rm{sin}}\delta {\rm{cos}}\lambda {\rm{sin}}2\varphi-{\rm{sin}}2\delta {\rm{sin}}\lambda {\rm{co}}{{\rm{s}}^2}\varphi )\\ {M_3} = {M_0}\left( {\sin 2\delta \sin \lambda } \right)\\ {M_4} = {M_0}({\rm{sin}}\delta {\rm{cos}}\lambda {\rm{cos}}2\varphi + \frac{1}{2}{\rm{sin}}2\delta {\rm{sin}}\lambda {\rm{si}}{{\rm{n}}^2}\varphi )\\ {M_5} =-{M_0}({\rm{cos}}\delta {\rm{cos}}\lambda {\rm{cos}}\varphi + {\rm{cos}}2\delta {\rm{sin}}\lambda {\rm{sin}}\varphi )\\ {M_6} = - {M_0}({\rm{cos}}\delta {\rm{cos}}\lambda {\rm{sin}}\varphi - {\rm{cos}}2\delta {\rm{sin}}\lambda {\rm{cos}}\varphi ) \end{array} $ | (4) |
式中,M0为标量地震矩,φ为断层走向角,δ为倾角,λ为滑动角。
模拟地震波采用以上述理论为基础的Mineos(http://www.geodynamics.org/cig/software/mineos)计算,其中一维地球模型采用PREM模型[14],断层参数采用global CMT提供的震源机制解。
引入比例因子S描述简正模观测值与模拟值的拟合程度,S定义为:
| $ S = \sum\limits_{i = 1}^n {{O_i}{S_i}/} \sum\limits_{i = 1}^n {S_i^2} $ | (5) |
式中,Oi和Si分别为简振模观测值和模拟值的振幅值,n为选择计算的频率点个数。因为断层运动参数对球型简振模的影响比较小,在简振模观测值和模拟值拟合时可认为M0为常数,因此S越接近于1说明两种简振模的拟合程度越高,表明地下结构与横向均匀模型越接近。
1.3 简振模对应的深度范围利用PREM地球参考模型,计算球型简振模的本征频率和本征函数,获得球型简振模的能量密度谱,经计算得到球型简振模可以到达上地幔的深度范围。0S12、0S33、0S54和0S82对应的频率分别为1.990 4 mHz、4.084 5 mHz、5.974 1 mHz和8.556 8 mHz,简振模的能量密度-深度分布如图 3所示。

|
图 3 球型简振模的能量密度-深度分布 Fig. 3 Energy densities-depths diagram for spherical modes 实线为剪切波能量,虚线为压缩波能量,竖直线为深度标记(仅地幔) |
图 3中4个简振模0S12、0S33、0S54和0S82的能量密度-深度主要分布范围分别为660~1 100 km、220~660 km、150~320 km和110~240 km。可知,频率为3.0~6.0 mHz的简振模可达上地幔的深度大概为200~660 km。
2 观测与比较参与比较的宽频带地震仪观测值、超导重力仪观测值和Mineos模拟值经过傅里叶变换得到线性振幅谱,从图 3可以看到部分球型简振模的谱峰。图 4为2008-02-20 Sumatera MW7.3地震简正模比较结果和以PREM模型计算的各频率简振模能到达上地幔的平均深度。可知,2.0~6.0 mHz范围内两种简振模拟合得很好,但在6.0 mHz之后观测值振幅比模拟值振幅下降速度快,出现较大偏差,且在所有比较结果中都会出现。

|
图 4 2008-02-20 Sumatera MW7.3地震西安台站简振模对比 Fig. 4 Spheroidal modes comparison of synthetic and observed results of Xi'an station about the Sumatera MW 7.3 earthquake on February 20, 2008 数据长度为6h,作 Hanning窗傅里叶变换,竖直虚线为理论简振模频率,下图均与此相同 |
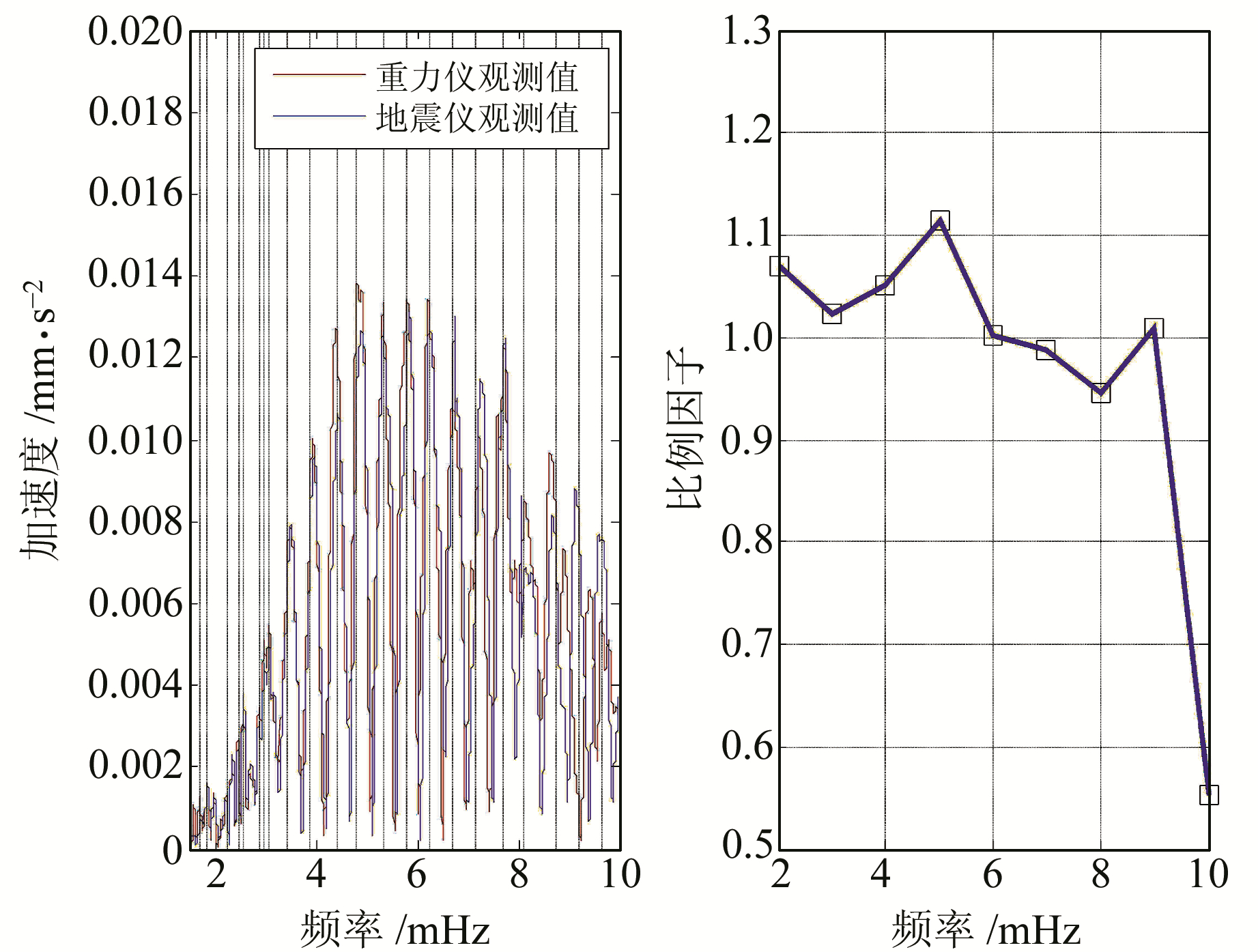
选用与地震台相邻的超导重力仪数据约束宽频带地震仪低频标定问题。同一地震发生后,相邻的不同台站接收相同路径传播的地震面波,而小区域的地下结构对地震面波的影响较小,可以认为相邻或者相近台站接收到的数据是一致的。图 5为2013-10-25日本Honshu MW7.1地震后恩施地震台和武汉超导台的比较及比例因子。结果显示,在2.0~6.5 mHz范围内观测值吻合良好,且比例因子S在0.9~1.1之间,表明恩施台宽频带地震仪没有低频标定问题,证明了利用宽频带地震仪记录球型简振模的有效性。
|
图 5 2013-10-25日本Honshu MW7.1地震在恩施地震台和武汉超导台的比较 Fig. 5 Spheroidal modes comparison of observed results of Enshi station and Wuhan superconducting station about Honshu of Japan MW7.1 earthquake on October 25, 2013 |
图 6为2013-10-25日本Honshu MW7.1地震后西安、恩施和昆明台宽频带地震仪以及武汉台超导重力仪的观测值与模拟值的比较和比例因子S。与图 5类似,图 6结果显示,宽频带地震仪观测值和超导重力仪观测值、宽频带地震仪观测值和模拟值、超导重力仪观测值和模拟值均拟合良好,且在3.0~6.0 mHz范围内,S值基本在0.9~1.1之间,进一步说明超导重力仪数据可以很好地约束宽频带地震仪数据,也说明利用两种数据的记录值进行介质横向特性分析的有效性。

|
图 6 2013-10-25日本Honshu MW7.1地震在各台站的观测值与模拟值比较 Fig. 6 Spheroidal modes comparison of simulated and observed results on Honshu of Japan MW7.1 earthquake on October 25, 2013 |
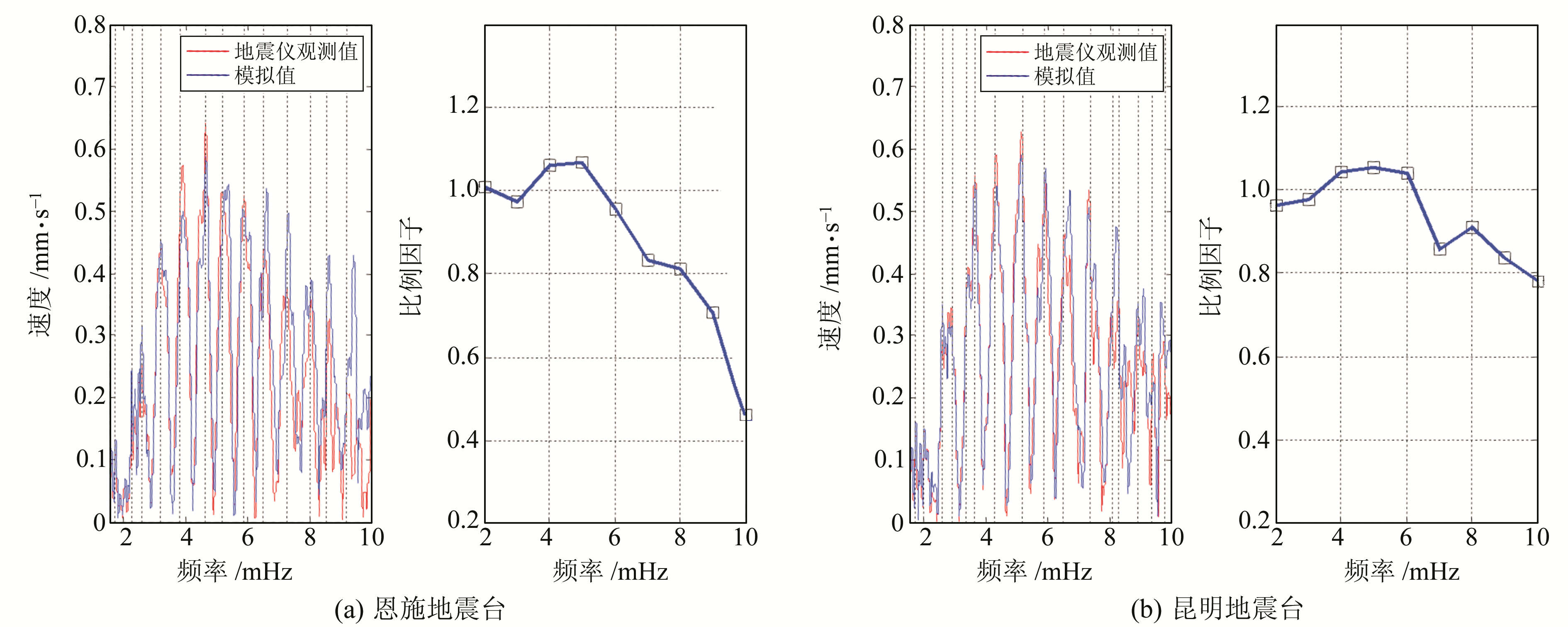
图 7为2008-03-20新疆MW7.1地震后恩施和昆明台宽频带地震仪观测值与模拟值的比较和比例因子S。结果显示,两个地震台观测值均拟合得很好。比较图 5~7发现,除了个别振幅谱大小有差异外,其余观测值和模拟值振幅在3.0~6.0 mHz基本吻合且不存在频率偏移,比例因子S均在0.9~1.1的范围内,说明仪器记录值和以横向均匀模型计算的模拟值很接近。
|
图 7 2008-03-20新疆MW7.1地震在恩施和昆明地震台的观测值与模拟值比较 Fig. 7 Spheroidal modes comparison of simulated and observed results on Xinjiang MW7.1 earthquake on October 25, 2013 |
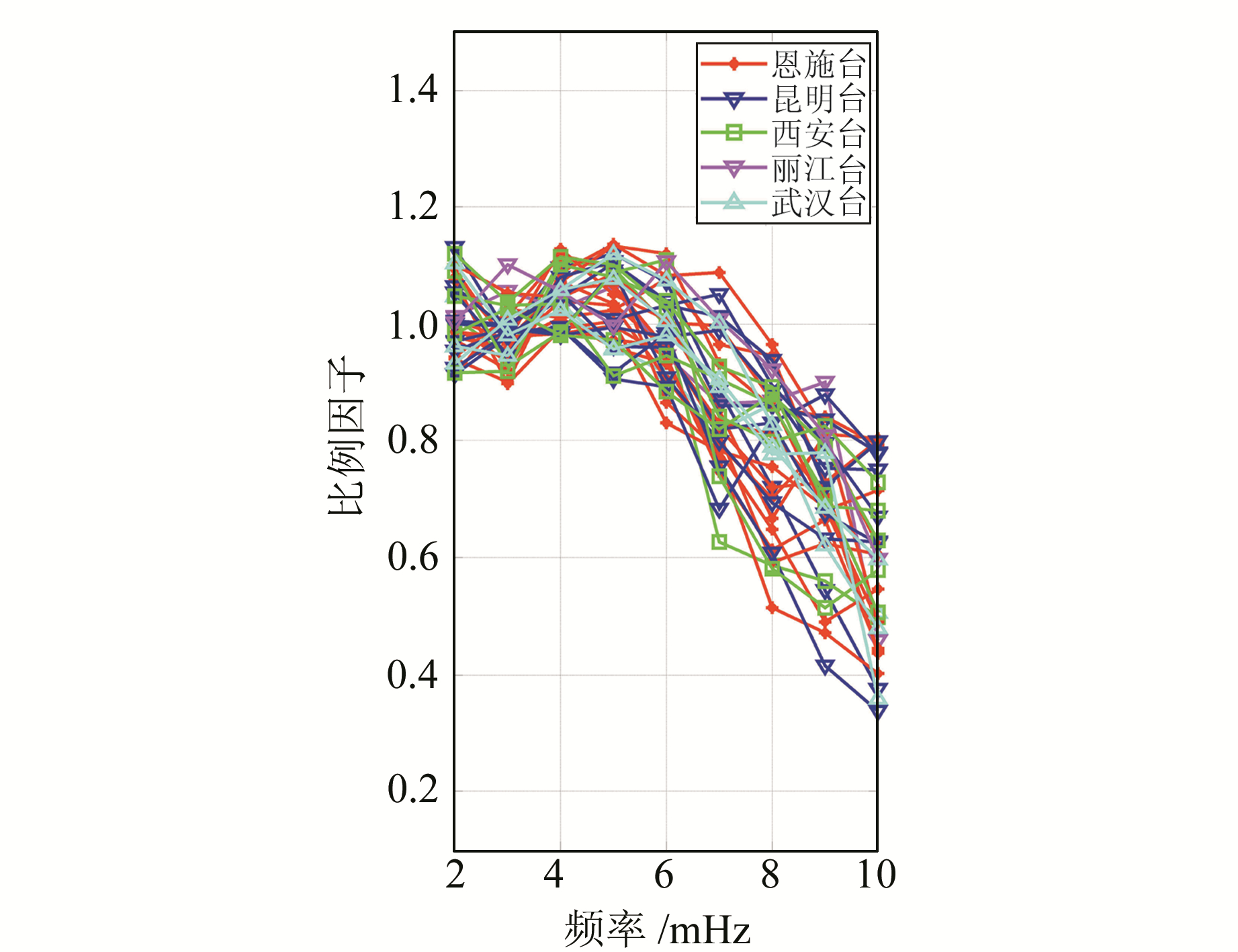
为了说明各简振模观测值和模拟值的拟合程度,从图 5~7及其他地震对比的结果中统计2.0~6.0 mHz范围内比例因子S的值,共有36条曲线,结果如图 8和表 2所示。从图 8中看出,S值在2.0~6.0 mHz基本保持在1附近且曲线较平缓,而在6.0 mHz之后迅速下降,说明在小于6.0 mHz的其他频率的简振模观测值和模拟值拟合很好。表 2说明在3.0~6.0 mHz范围内,至少83%的S值在0.9~1.1之间,其他不在该范围的S值主要是大于1.1,可能是受标量地震矩M0较大、地震类型、震源深度和震中距的影响。由此可知,在3.0~6.0 mHz范围内,简振模的观测值和模拟值拟合得比较好。
|
图 8 所有台站的比例因子S Fig. 8 The scaling factors S of all stations |
|
|
表 2 台站比例因子S统计 Tab. 2 Statistics of scaling factors S |
1) 根据Park[15]的研究,上地幔横向不均匀引起的球型简振-环形简振模(S-T)耦合会明显降低3.0~6.0 mHz范围内球型简正模的振幅,同时还存在谱峰偏移。但本文结果显示,3.0~6.0 mHz两种简振模振幅大小相当,谱峰偏移也并不明显,说明台站覆盖区域上地幔并未出现大范围横向不均匀引起的S-T耦合。
2) 频率为5.974 1 mHz的简振模0S54和4.084 5 mHz的0S33的能量密度谱峰分别分布在上地幔150~320+ km和220~660+ km深度范围,本文中的台站覆盖区域上地幔200~660 km内没有大范围的横向不均匀结构。
| [1] |
Stein S, Okal E A. Seismology: Speed and Size of the Sumatra Earthquake[J]. Nature, 2005, 434(7033): 581-582 DOI:10.1038/434581a
(  0) 0) |
| [2] |
严珍珍, 张怀, 杨长春, 等. 地震激发地球自由振荡的数值模拟初步探索[J]. 地球科学进展, 2008, 23(10): 1021-1026 (Yan Zhenzhen, Zhang Huai, Yang Changchun, et al. An Initial Study of the Numerical Simulation of the Earth's Free Oscillations Process Excited by Earthquake[J]. Advance in Earth Science, 2008, 23(10): 1021-1026)
(  0) 0) |
| [3] |
刘子维, 郝洪涛, 韦进, 等. 利用SG-C053超导重力仪检测智利8.8级地震激发的地球自由振荡[J]. 大地测量与地球动力学, 2011, 31(增1): 43-45 (Liu Ziwei, Hao Hongtao, Wei Jin, et al. Detection of Earth's Free Oscillation Excited by Chile MS8.8 Earthquake by Using Superconducting Gravimeter[J]. Journal of Geodesy and Geodynamics, 2011, 31(S1): 43-45)
(  0) 0) |
| [4] |
江颖, 胡小刚, 刘成利, 等. 利用地球自由振荡观测约束庐山地震的震源机制解[J]. 中国科学:地球科学, 2014, 44(12): 2689-2696 (Jiang Ying, Hu Xiaogang, Liu Chengli, et al. Constraining the Focal Mechanism of the Lushan Earthquake with Observations of the Earth's Free Oscillations[J]. Science China Earth Sciences, 2014, 44(12): 2689-2696)
(  0) 0) |
| [5] |
卢造勋, 姜德禄, 白云, 等. 东北地区地壳上地幔结构的探测与研究[J]. 东北地震研究, 2005, 21(1): 1-8 (Lu Zaoxun, Jiang Delu, Bai Yun, et al. Exploration and Research on the Structure of the Crust and Upper Mantle in Northeast China[J]. Seismological Research of Northeast China, 2005, 21(1): 1-8)
(  0) 0) |
| [6] |
Aki K. Scaling Law of Seismic Spectrum[J]. Journal of Geophysical Research, 1967, 72(4): 1217-1231 DOI:10.1029/JZ072i004p01217
(  0) 0) |
| [7] |
Hu X G, Jiang Y, Sun H P. Assessing the Scalar Moment of Moderate Earthquake and the Effect of Lateral Heterogeneity on Normal Modes--An Example from the 2013/04/20 Lushan Earthquake, Sichuan, China[J]. Physics of the Earth and Planetary Interiors, 2014, 232: 61-71 DOI:10.1016/j.pepi.2014.04.005
(  0) 0) |
| [8] |
Ekström G, Dalton C A, Nettles M. Observations of Time-Dependent Errors in Long-Period Instrument Gain at Global Seismic Stations[J]. Seismological Research Letters, 2006, 77(1): 12-22 DOI:10.1785/gssrl.77.1.12
(  0) 0) |
| [9] |
Hinderer J, Florsch N, Mäkinen J, et al. On the Calibration of a Superconducting Gravimeter Using Absolute Gravity Measurements[J]. Geophysical Journal International, 1991, 106(2): 491-497 DOI:10.1111/gji.1991.106.issue-2
(  0) 0) |
| [10] |
Francis O, Niebauer T M, Sasagawa G, et al. Calibration of a Superconducting Gravimeter by Comparison with an Absolute Gravimeter FG5 in Boulder[J]. Geophysical Research Letters, 1998, 25(7): 1075-1078 DOI:10.1029/98GL00712
(  0) 0) |
| [11] |
Sun H P, Chen X D, Hsu H T, et al. Accurate Determination of Calibration Factor for Tidal Gravity Observation of a GWR-Superconducting Gravimeter[J]. Acta Seismologica Sinica, 2001, 14(6): 692-700 DOI:10.1007/BF02718080
(  0) 0) |
| [12] |
Gilbert F. Derivation of Source Parameters from Low-Frequency Spectra[J]. Philosophical Transactions of the Royal Society of London, 1973, 274(1239): 369-371 DOI:10.1098/rsta.1973.0065
(  0) 0) |
| [13] |
Jost M L, Herrmann R B. A Student's Guide to and Review of Moment Tensors[J]. Seismological Research Letters, 1989, 60(2): 37-57
(  0) 0) |
| [14] |
Dziewonski A M, Anderson D L. Preliminary Reference Earth Model[J]. Physics of the Earth and Planetary Interiors, 1981, 25(4): 297-356 DOI:10.1016/0031-9201(81)90046-7
(  0) 0) |
| [15] |
Park J. Asymptotic Coupled-Mode Expressions for Multiplet Amplitude Anomalies and Frequency Shifts on an Aspherical Earth[J]. Geophysical Journal International, 1987, 90(1): 129-169 DOI:10.1111/j.1365-246X.1987.tb00679.x
(  0) 0) |
2. College of Earth Science, University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China
 2018, Vol. 38
2018, Vol. 38















