2. 武汉大学测绘学院,武汉市珞喻路129号,430079;
3. 东华理工大学江西省数字国土重点实验室,南昌市广兰大道418号,330013
高铁运行速度快,对线路的稳定性、平顺性要求高[1]。高铁路基沉降观测有利于控制路堤填筑的速度,保证路堤填筑的稳定性。通过预测沉降量,能确定路基是否平稳,为何时开始轨道施工提供理论依据[2]。高铁路基前期沉降量大,后期逐渐减慢,最后趋于稳定,而灰色理论作为一种预测理论,其线性变化遵循高铁路基沉降变化规律,并且能深入挖掘路基变形的内在信息,具有建模简单、要求的样本数据少、运用方便等优势,广泛应用于高铁路基沉降预测[3]。灰色理论GM(1, 1)是在最小二乘(LS)条件下对经典的Gauss-Markov模型L=Bx进行求解[4]。但当观测数据L包含误差时,观测数据一次累加形成的系数矩阵B同样包含误差,如果再使用LS求解,计算出的未知参数是有偏的[5]。总体最小二乘(TLS)算法兼顾观测矩阵和系数矩阵的误差,TLS解被证明具有渐进无偏性[6-7]。
路基观测值有时不可避免地包含少量粗差,如果不剔除,会使GM(1, 1)模型扭曲,预测结果错误。因此,需要稳健算法对粗差进行定位和剔除[7]。本文先提出部分变量误差模型的总体最小二乘估计(partial errors-in variables total least squares,PEIV-TLS),在此基础上,提出基于IGGⅢ抗差方案[8]的部分变量的总体最小二乘稳健估计(robust partial errors-in-variables total least squares based on IGGⅢ function,PEIV-TLS-IGGⅢ)。仿真数据和工程实例数据验证了模型的优越性。
1 PEIV-TLS-IGGⅢ稳健估计GM(1, 1)白化微分方程式为:
| $ \frac{{{\rm{d}}{\mathit{\boldsymbol{x}}^{\left( 1 \right)}}}}{{{\rm{d}}t}} + a{\mathit{\boldsymbol{x}}^{\left( 1 \right)}} = b $ | (1) |
式中,x(1)为对路基数据进行一次累加,a为发展系数,控制系统发展态势的大小,b为灰色作用量,反映数据的变化关系。
参数向量为:
| $ \mathit{\boldsymbol{\hat a}} = {\left[ {\begin{array}{*{20}{c}} a&b \end{array}} \right]^{\rm{T}}} $ | (2) |
令
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} { - 0.5\left( {{x^{\left( 1 \right)}}\left( 1 \right) + {x^{\left( 1 \right)}}\left( 2 \right)} \right)}&1\\ { - 0.5\left( {{x^{\left( 1 \right)}}\left( 2 \right) + {x^{\left( 1 \right)}}\left( 3 \right)} \right)}&1\\ \vdots&\vdots \\ { - 0.5\left( {{x^{\left( 1 \right)}}\left( {n - 1} \right) + {x^{\left( 1 \right)}}\left( n \right)} \right)}&1 \end{array}} \right] $ |
| $ \mathit{\boldsymbol{L}} = {\left[ {\begin{array}{*{20}{c}} {{x^{\left( 0 \right)}}\left( 2 \right)}&{{x^{\left( 0 \right)}}\left( 3 \right)}& \cdots &{{x^{\left( 0 \right)}}\left( n \right)} \end{array}} \right]^{\rm{T}}} $ |
式(1)可以表示为:
| $ \mathit{\boldsymbol{L}} + {{\mathit{\boldsymbol{ \varepsilon }}}_y} = \mathit{\boldsymbol{B}} \cdot \mathit{\boldsymbol{\hat a}} $ | (3) |
根据最小二乘原理可得未知参数的估值为:
| $ \mathit{\boldsymbol{\hat a}} = {\left[ {\begin{array}{*{20}{c}} a&b \end{array}} \right]^{\rm{T}}} = {\left[ {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B}}} \right]^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{L}} $ | (4) |
由式(4)可知,最小二乘方法求未知参数时,只考虑了系数矩阵L的误差。但是,系数矩阵B的第1列的数是由观测数据一次累加和的平均,当观测数据含有误差时,系数矩阵B也会含有误差。PEIV-TLS-IGGⅢ方法能够同时兼顾系数矩阵B中部分变量误差的影响,同时还具有一定的抗差能力。GM(1, 1)的PEIV-TLS-IGGⅢ误差模型为:
| $ \begin{array}{*{20}{c}} {\varphi \left( {{\mathit{\boldsymbol{e}}_y},{\mathit{\boldsymbol{e}}_B},\mathit{\boldsymbol{\hat a}}} \right) = \mathit{\boldsymbol{L}} + {\mathit{\boldsymbol{e}}_y} - \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1} + {\mathit{\boldsymbol{e}}_B}}&{{\mathit{\boldsymbol{B}}_2}} \end{array}} \right] \cdot \mathit{\boldsymbol{\hat a}}}\\ {{\mathit{\boldsymbol{e}}_y} \in {R^{n \times 1}},{\mathit{\boldsymbol{e}}_B} \in {R^{n \times 1}}} \end{array} $ | (5) |
式中,n为白化微分方程的个数,L为观测值的真值,B1为系数矩阵中含有误差变量的真值,B2为n行1列全为1的矩阵,ey和eB分别为观测值和系数矩阵误差的大小。
随机模型为:
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}_y}}\\ {{\mathit{\boldsymbol{e}}_B}} \end{array}} \right] \propto N\left( {\left[ \begin{array}{l} 0\\ 0 \end{array} \right],\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_L}}&0\\ 0&{{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_B}} \end{array}} \right]} \right) $ | (6) |
令未知参数ey、eB和
| $ \begin{array}{*{20}{c}} {f\left( {{\mathit{\boldsymbol{e}}_y},{\mathit{\boldsymbol{e}}_B},a} \right) \approx \varphi \left( {\mathit{\boldsymbol{e}}_y^0,\mathit{\boldsymbol{e}}_B^0,{{\mathit{\boldsymbol{\hat a}}}^0}} \right) + {\mathit{\boldsymbol{B}}_{10}}\left( {{\mathit{\boldsymbol{e}}_y} - \mathit{\boldsymbol{e}}_y^0} \right) + }\\ {{\mathit{\boldsymbol{B}}_{20}}\left( {{\mathit{\boldsymbol{e}}_B} - \mathit{\boldsymbol{e}}_B^0} \right) + {\mathit{\boldsymbol{A}}_0}\left( {\mathit{\boldsymbol{\hat a}} - {{\mathit{\boldsymbol{\hat a}}}^0}} \right) = 0} \end{array} $ | (7) |
其中,
| $ {\mathit{\boldsymbol{B}}_{10}} = \frac{{\partial \varphi \left( {{\mathit{\boldsymbol{e}}_y},{\mathit{\boldsymbol{e}}_B},\mathit{\boldsymbol{\hat a}}} \right)}}{{\partial {\mathit{\boldsymbol{e}}_y}}},{\mathit{\boldsymbol{B}}_{20}} = \frac{{\partial \varphi \left( {{\mathit{\boldsymbol{e}}_y},{\mathit{\boldsymbol{e}}_B},\mathit{\boldsymbol{\hat a}}} \right)}}{{\partial {\mathit{\boldsymbol{e}}_B}}}, $ |
| $ {\mathit{\boldsymbol{A}}_0} = \frac{{\partial \varphi \left( {{\mathit{\boldsymbol{e}}_y},{\mathit{\boldsymbol{e}}_B},\mathit{\boldsymbol{\hat a}}} \right)}}{{\partial \mathit{\boldsymbol{\hat a}}}} $ |
令
| $ {\mathit{\boldsymbol{W}}^0} = \varphi \left( {\mathit{\boldsymbol{e}}_y^0,\mathit{\boldsymbol{e}}_B^0,{{\mathit{\boldsymbol{\hat a}}}^0}} \right) - {\mathit{\boldsymbol{B}}_{10}}\mathit{\boldsymbol{e}}_y^0 - {\mathit{\boldsymbol{B}}_{20}}\mathit{\boldsymbol{e}}_B^0 $ | (8) |
则可得观测方程:
| $ {\mathit{\boldsymbol{B}}_{10}}{\mathit{\boldsymbol{e}}_y} + {\mathit{\boldsymbol{B}}_{20}}{\mathit{\boldsymbol{e}}_B} + {\mathit{\boldsymbol{A}}_0}\left( {\mathit{\boldsymbol{\hat a}} - {{\mathit{\boldsymbol{\hat a}}}^0}} \right) + {\mathit{\boldsymbol{W}}^0} = 0 $ | (9) |
IGGⅢ抗差方案充分考虑了实际观测数据,具有良好的抵御粗差能力[9],其权因子为:
| $ \mathit{\boldsymbol{W}}\left( u \right) = \left\{ {\begin{array}{*{20}{c}} {1,\left| u \right| < {k_0}}\\ {\frac{{{k_0}}}{{\left| u \right|}}{{\left( {\frac{{{k_1} - \left| u \right|}}{{{k_1} - {k_0}}}} \right)}^2},{k_0} \le \left| u \right| < {k_1}}\\ {0,\left| u \right| \ge {k_1}} \end{array}} \right. $ | (10) |
式中,u表示标准化残差(u=
由式(10)可知,观测向量L和系数矩阵B的权因子矩阵分别为:
| $ \begin{array}{l} {\mathit{\boldsymbol{W}}_y} = {\rm{diag}}\left( {{\mathit{\boldsymbol{W}}_{y,1}},{\mathit{\boldsymbol{W}}_{y,2}}, \cdots {\mathit{\boldsymbol{W}}_{y,n}}} \right),\\ {\mathit{\boldsymbol{W}}_B} = {\rm{diag}}\left( {{\mathit{\boldsymbol{W}}_{B,1}},{\mathit{\boldsymbol{W}}_{B,2}}, \cdots {\mathit{\boldsymbol{W}}_{B,n}}} \right) \end{array} $ | (11) |
设初始权阵为Py和PB,其权因子初值均为1,即Py=PB=diag(1, 1, …, 1)∈Rn×n, 则经过IGGⅢ方案后得到相应的权阵P1=Py×Wy,P2=PB×WB,相应的协因数阵为Q1=P2-1,Q2=P2-1。
利用拉格朗日乘数λ构造目标函数[10]:
| $ \begin{array}{*{20}{c}} {\mathit{\Phi }\left( {{\mathit{\boldsymbol{e}}_y},{\mathit{\boldsymbol{e}}_B},\mathit{\boldsymbol{\lambda }},\mathit{\boldsymbol{\hat a}}} \right) = \mathit{\boldsymbol{e}}_y^{\rm{T}}\mathit{\boldsymbol{Q}}_1^{ - 1}{\mathit{\boldsymbol{e}}_y} + \mathit{\boldsymbol{e}}_B^{\rm{T}}\mathit{\boldsymbol{Q}}_2^{ - 1}{\mathit{\boldsymbol{e}}_B} - 2{\mathit{\boldsymbol{\lambda }}^{\rm{T}}}}\\ {\left[ {{\mathit{\boldsymbol{B}}_{10}}{\mathit{\boldsymbol{e}}_y} + {\mathit{\boldsymbol{B}}_{20}}{\mathit{\boldsymbol{e}}_B} + {\mathit{\boldsymbol{A}}_0}\left( {\mathit{\boldsymbol{\hat a}} - {{\mathit{\boldsymbol{\hat a}}}^0}} \right) + {\mathit{\boldsymbol{W}}^0}} \right]} \end{array} $ | (12) |
对未知函数求偏导:
| $ \frac{{\partial \mathit{\Phi }}}{{2\partial {\mathit{\boldsymbol{e}}_y}}} = \mathit{\boldsymbol{e}}_y^{\rm{T}}\mathit{\boldsymbol{Q}}_1^{ - 1} - {\mathit{\boldsymbol{\lambda }}^{\rm{T}}}{\mathit{\boldsymbol{B}}_{10}} = 0 $ | (13) |
| $ \frac{{\partial \mathit{\Phi }}}{{2\partial {\mathit{\boldsymbol{e}}_B}}} = \mathit{\boldsymbol{e}}_B^{\rm{T}}\mathit{\boldsymbol{Q}}_2^{ - 1} - {\mathit{\boldsymbol{\lambda }}^{\rm{T}}}{\mathit{\boldsymbol{B}}_{20}} = 0 $ | (14) |
| $ \frac{{\partial \mathit{\Phi }}}{{2\partial \mathit{\boldsymbol{\hat a}}}} = - {\mathit{\boldsymbol{\lambda }}^{\rm{T}}}{\mathit{\boldsymbol{A}}_0} = 0 $ | (15) |
| $ \frac{{\partial \mathit{\Phi }}}{{2\partial \mathit{\boldsymbol{\lambda }}}} = - \left( {{\mathit{\boldsymbol{B}}_{10}}{\mathit{\boldsymbol{e}}_y} + {\mathit{\boldsymbol{B}}_{20}}{\mathit{\boldsymbol{e}}_B} + {\mathit{\boldsymbol{A}}_0}\left( {\mathit{\boldsymbol{\hat a}} - {{\mathit{\boldsymbol{\hat a}}}^0}} \right) + \mathit{\boldsymbol{W}}} \right) = 0 $ | (16) |
令
| $ \mathit{\boldsymbol{N}} = {\mathit{\boldsymbol{B}}_{10}}{\mathit{\boldsymbol{Q}}_1}\mathit{\boldsymbol{B}}_{10}^{\rm{T}} + {\mathit{\boldsymbol{B}}_{20}}{\mathit{\boldsymbol{Q}}_2}\mathit{\boldsymbol{B}}_{20}^{\rm{T}} $ | (17) |
则:
| $ \mathit{\boldsymbol{\hat a}} = - {\left[ {\mathit{\boldsymbol{A}}_0^{\rm{T}}{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{A}}_0}} \right]^{ - 1}}\mathit{\boldsymbol{A}}_0^{\rm{T}}{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{W}}^0} + {{\mathit{\boldsymbol{\hat a}}}^0} $ | (18) |
| $ \mathit{\boldsymbol{\lambda }} = - {\mathit{\boldsymbol{N}}^{ - 1}}\left[ {{\mathit{\boldsymbol{A}}_0}\left( {\mathit{\boldsymbol{\hat a}} - {{\mathit{\boldsymbol{\hat a}}}^0}} \right) + {\mathit{\boldsymbol{W}}^0}} \right] $ | (19) |
相应的残差向量为:
| $ \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat e}}}_y}}\\ {{{\mathit{\boldsymbol{\hat e}}}_B}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Q}}_1}\mathit{\boldsymbol{B}}_{10}^{\rm{T}}}\\ {{\mathit{\boldsymbol{Q}}_2}\mathit{\boldsymbol{B}}_{20}^{\rm{T}}} \end{array}} \right]\mathit{\boldsymbol{\lambda }} $ | (20) |
将
计算得到
| $ {{\hat x}^{\left( 1 \right)}}\left( {t + 1} \right) = \left( {{x^{\left( 0 \right)}}\left( 1 \right) - \frac{b}{a}} \right){{\rm{e}}^{ - at}} + \frac{b}{a} $ | (21) |
通过一次累减生成GM(1, 1)预测值:
| $ {{\hat x}^{\left( 0 \right)}}\left( {t + 1} \right) = \left( {1 - {{\rm{e}}^a}} \right)\left( {{x^{\left( 0 \right)}}\left( 1 \right) - \frac{b}{a}} \right) \times {{\rm{e}}^{ - at}} $ | (22) |
当PEIV-TLS-IGGⅢ方法中不经过IGGⅢ抗差方案处理时,就退化成为部分变量误差模型的总体最小二乘估计(PEIV-TLS),当IGGⅢ抗差方案和最小二乘进行组合,就形成了稳健最小二乘估计(LS-IGGⅢ)。
2 模拟实验设计根据高铁路基沉降规律,现取发展系数a=0.2,b=2,初始观测值为1.812 7 mm,通过式(22)得到21位模拟观测值。为验证LS、PEIV-TLS、PEIV-TLS-IGGⅢ的稳定性和可靠性,采用如下两种方案进行模拟实验。
方案一 在模拟的观测数据中添加服从正态分布N(0,σ2 Ι)(σ2=0.2, Ι为单位阵)的随机误差,并令第3位观测值为3 mm (远大于3倍中误差),多次重复实验,求各模型的稳定性。
方案二 粗差为2个,粗差的大小从0 mm增加到4 mm,步长为0.01 mm,求各模型的抗差能力。各模型分析结果见表 1。
|
|
表 1 各模型实验对比分析 Tab. 1 Comparison and analysis on models |
当模拟数据中不含有误差时,LS、PEIV-TLS、PEIV-TLS-IGGⅢ能得出相同的估计值,且估计结果无误差。当在模拟变量中加入一个粗差和一个方差为0.2的随机误差时,由表 1可知,LS的估计值a、b偏离真值最大,估计结果不再具有无偏性,但LS估计值a、b的方差最小,计算结果最稳定。在模拟实验中,PEIV-TLS方法比LS方法多引入20个系数变量,PEIV-TLS因为考虑到了系数矩阵的误差,并在总体均方差最小的情况下求解各变量值。由表 1可知,PEIV-TLS较LS方法a、b的精度分别提高了0.011和0.106,后验比也减少了0.045。而PEIV-TLS-IGGⅢ方法因为在部分变量总体最小二乘基础上引入了IGGⅢ抗差方案,所以具有一定的抗差性能。由表 1可知,PEIV-TLS-IGGⅢ方法a、b估计值效果最好,最接近真值,后验比最小,达到一级精度要求。
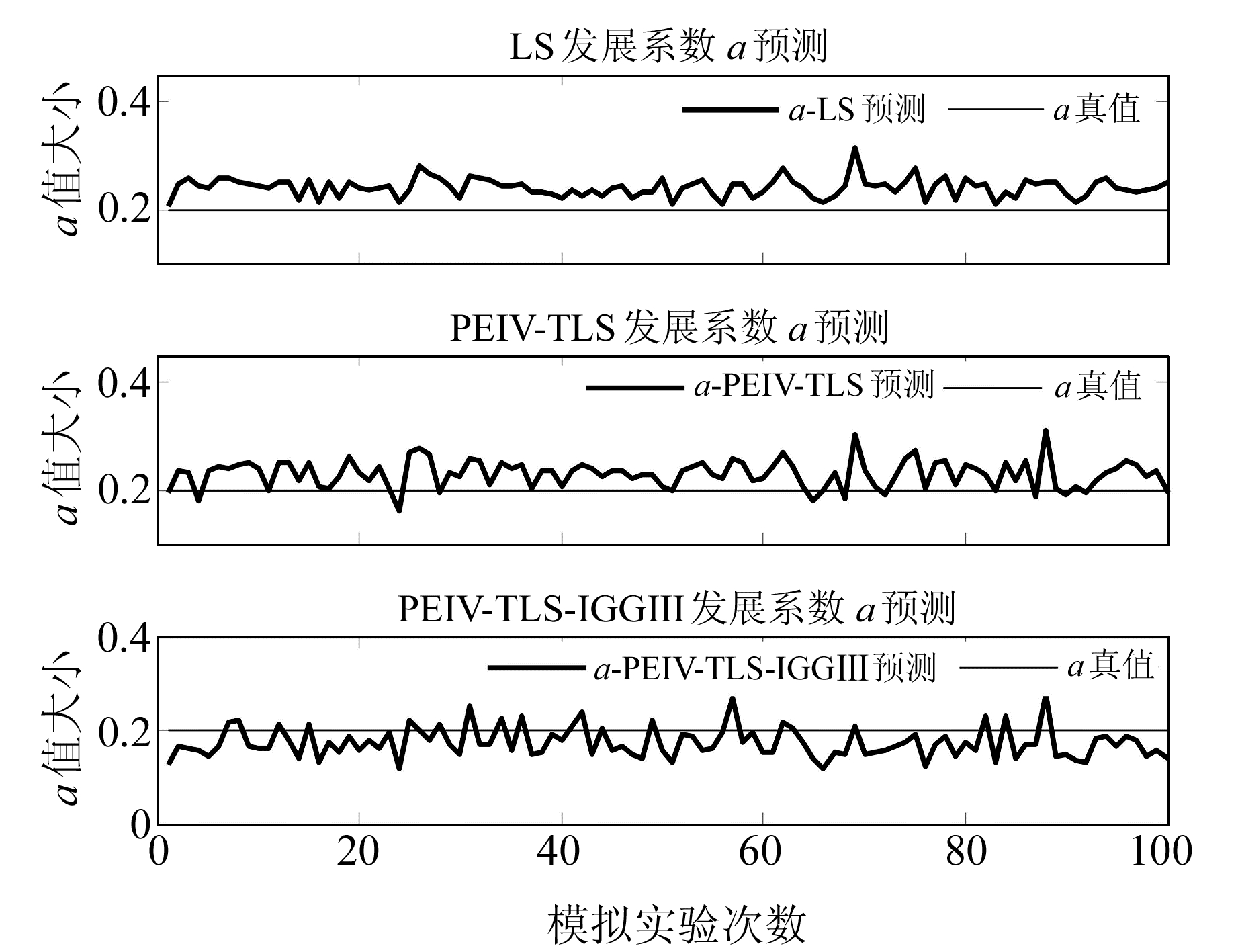
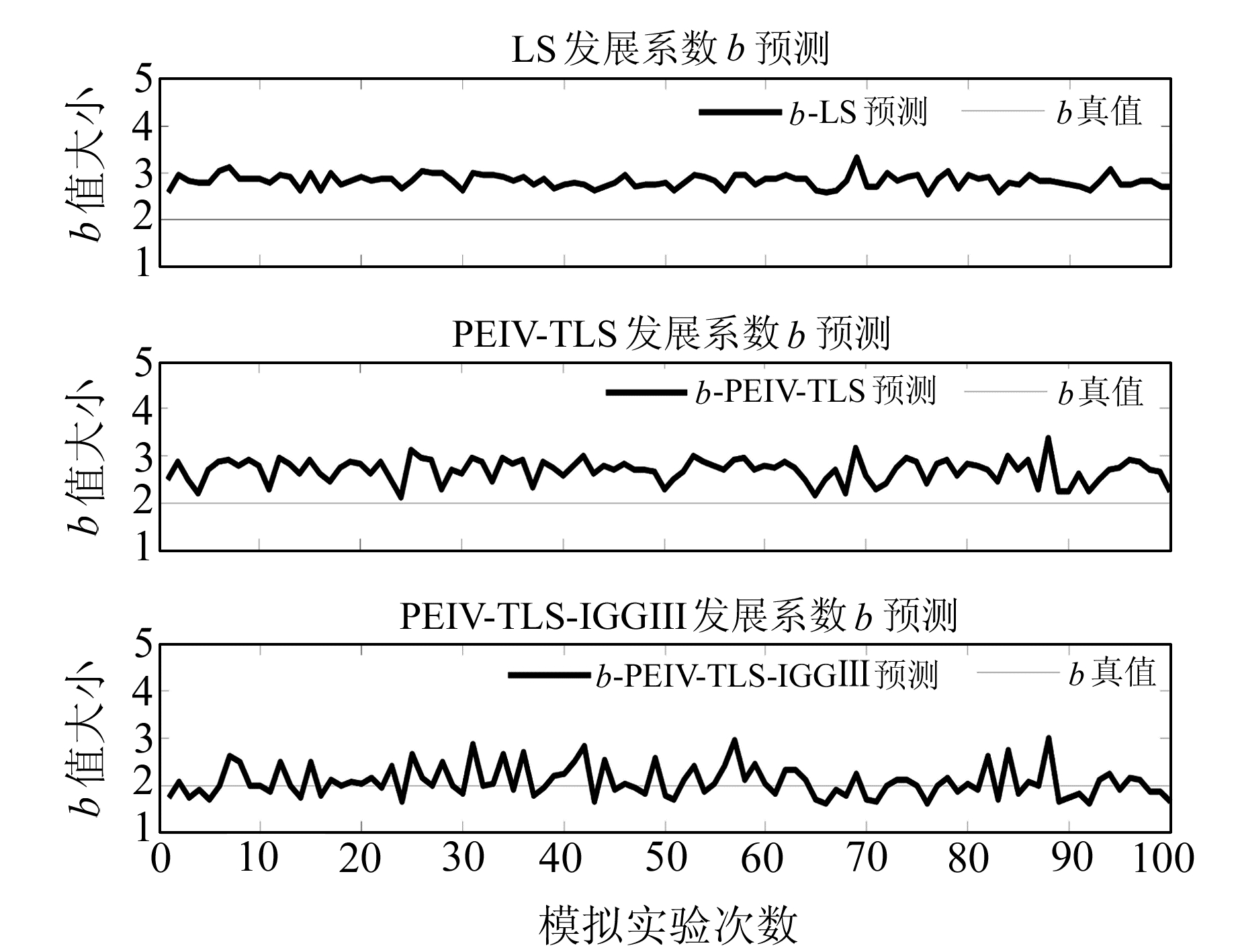
由图 1可以看出,在发展系数a的预测中,LS预测值明显偏离真值,预测精度最差;PEIV-TLS方法预测值开始靠近真值,但预测结果波动较大,预测值不稳定;PEIV-TLS-IGGⅢ方法能够不受粗差的影响,预测结果围绕a真值上下波动。由图 2可以看出,LS方法b预测值严重偏离实际值;PEIV-TLS方法开始向真值靠拢;PEIV-TLS-IGGⅢ方法b预测值围绕真值上下波动。所以,当观测数据中含有粗差时,PEIV-TLS-IGGⅢ方法预测效果最好。
|
图 1 方案一发展系数a预测图像 Fig. 1 The development coefficient of alphabet a prediction images |
|
图 2 方案一灰作用量b预测图像 Fig. 2 The grey action of alphabet b prediction images |
由表 1可知,当只含有1个或2个粗差时,LS估计a、b偏离真值最远,且随着粗差个数的增加,后验比也增加,表明LS方法不具有抗差性,预测效果最差;PEIV-TLS方法在只有1个粗差时,a值预测最准确,且方差最小,但b值的预测偏差相差0.37;PEIV-TLS-IGGⅢ方法只相差0.031,方差仅为0.012,预测效果最好,且后验比也最小。当粗差为2个时,各模型预测方法误差都增加,LS方法效果最差,完全无法使用;PEIV-TLS方法预测值方差偏大,预测值不稳定;PEIV-TLS-IGGⅢ方法预测也不准,偏差大,但后验比仍是最小的。
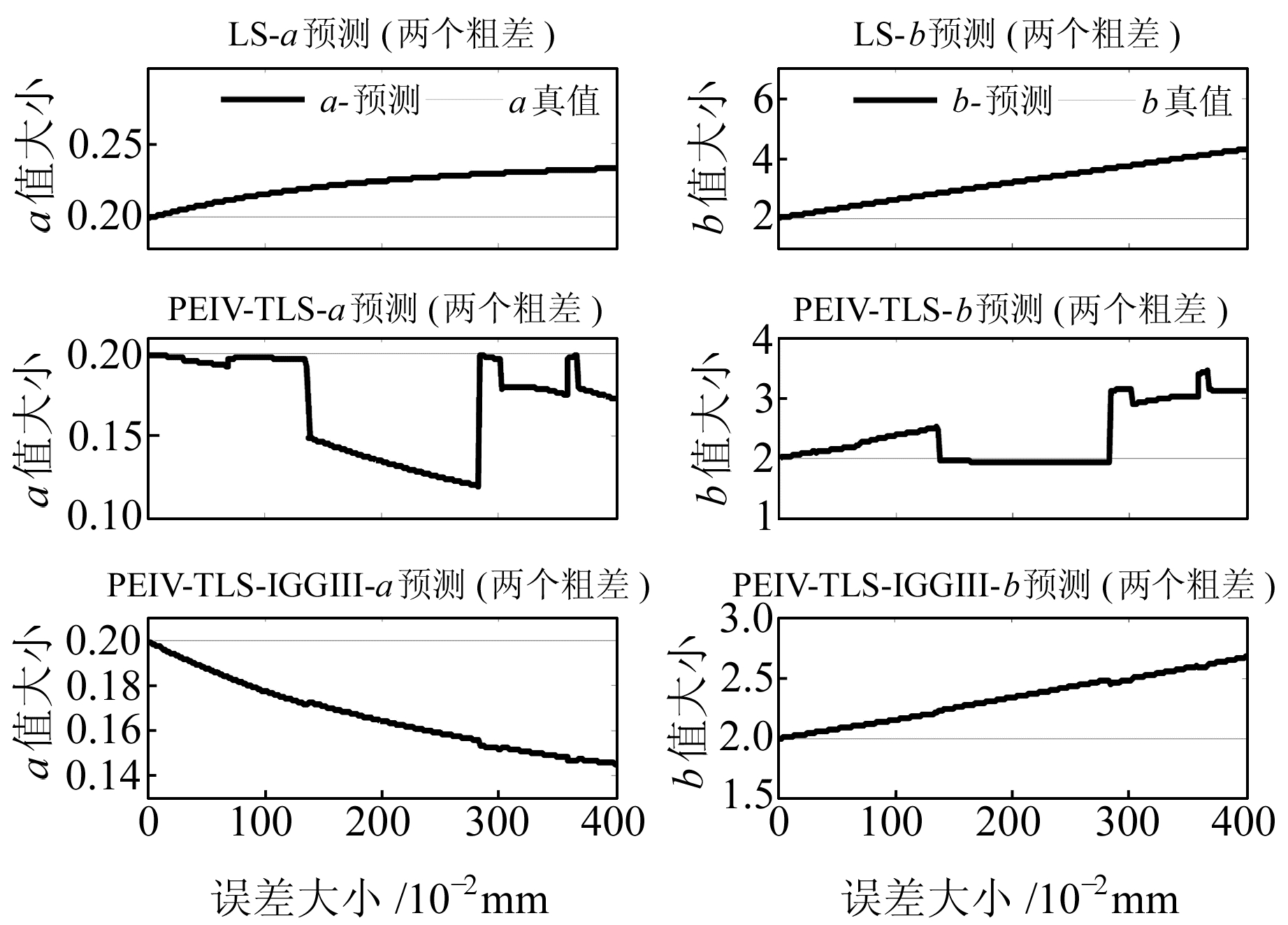
由图 3和图 4可以看出,当粗差增大时,预测曲线逐渐偏离真值。LS方法偏离真值的速率最快,后期完全无法使用;当存在2个粗差时,PEIV-TLS预测存在突变的现象,预测不稳定,其原因是引入了多个参数,且没有进行抗差处理;PEIV-TLS-IGGⅢ方法中a随粗差的增大而逐渐减小,b逐渐增大,预测效果仍是最佳。综上可知,当观测数据存在粗差时,LS估计不具有抗差性,预测偏差较大;PEIV-TLS方法预测不稳定,预测值方差较大;PEIV-TLS-IGGⅢ方法具有一定的抗差性,且预测稳定。

|
图 3 方案二含一个粗差各模型预测图像 Fig. 3 Scheme 2 prediction images with single outlier |
|
图 4 方案二含两个粗差各模型预测图像 Fig. 4 Scheme 2 prediction images with two outliers |
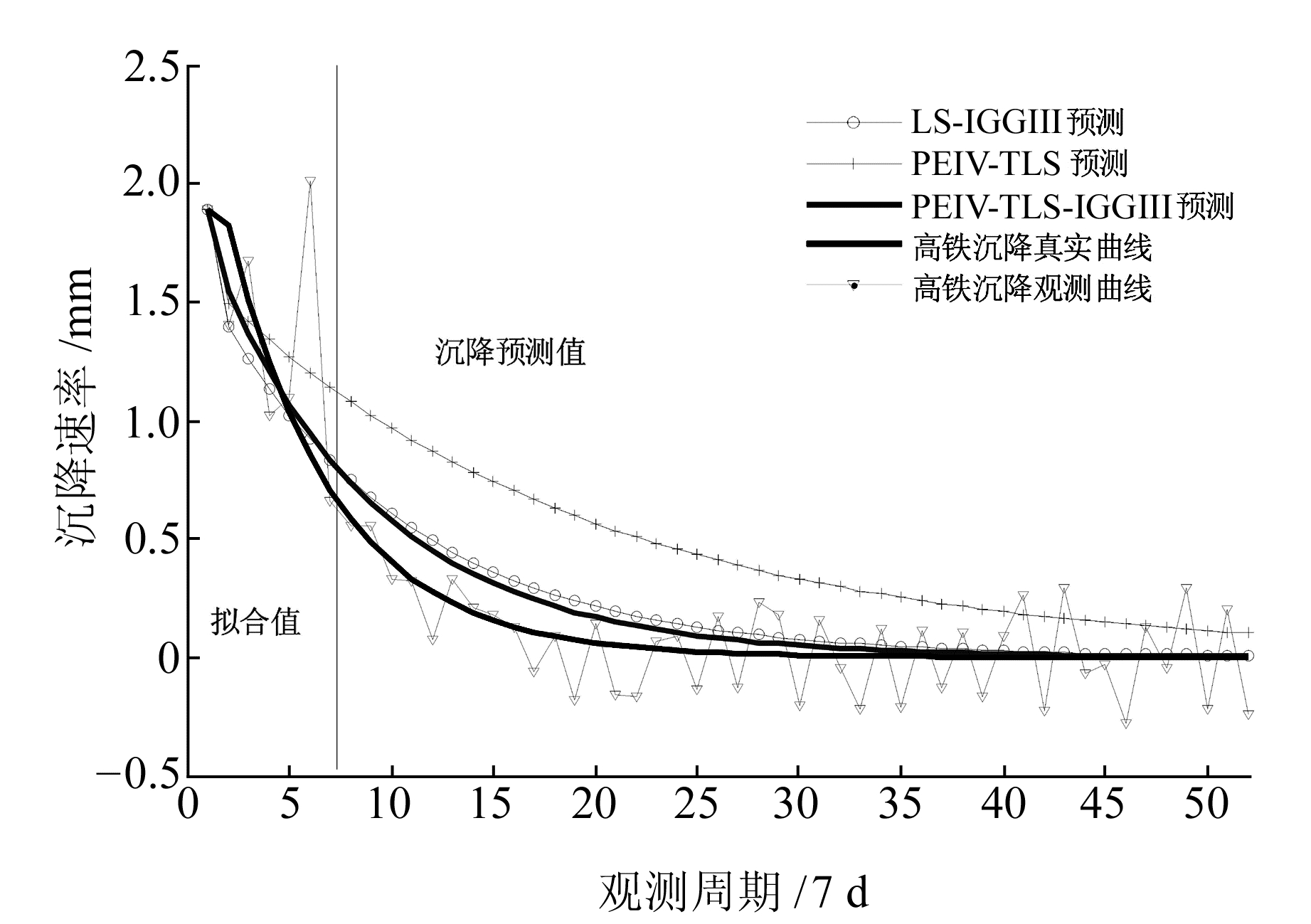
选用贵广高铁某监测点数据,其沉降监测周期为7 d。选取前52期沉降观测数据进行分析, 前7期数据建立LS-IGGⅢ、PEIV-TLS、PEIV-TLS-IGGⅢ模型,预测图像见图 5。
|
图 5 高铁路基沉降预测曲线图像 Fig. 5 High speed railway subsidence prediction image |
受光线、气温、仪器等随机因素影响,沉降变形监测数据不可避免地受到较大噪声干扰,因此沉降数据表现为较大的波动,需要对观测数据进行平差分析,识别高铁沉降真实曲线。利用前52期观测数据建立GM(1, 1)模型,可以计算出沉降真实曲线发展系数a=0.189, 灰作用量b=2.352。由图 5可知,沉降观测数据在第6期偏离真实数据较大,通过计算,该观测值包含粗差。在图 5中,PEIV-TLS预测曲线与真实沉降曲线的偏离程度远大于LS-IGGⅢ和PEIV-TLS-IGGⅢ预测曲线,说明观测数据中含有粗差时,预测模型的精度主要受粗差大小的影响,并且IGGⅢ抗差方案具有一定的抗差性。PEIV-TLS-IGGⅢ预测精度高于LS-IGGⅢ,说明观测方程中系数矩阵存在误差时,对观测方程进行总体最小二乘估计效果优于最小二乘估计。为比较各模型快速识别高铁路基沉降真实曲线的能力,选用前7~10期观测数据分别计算各模型发展系数a、灰作用量b预测值和后验比,计算结果见表 2。
|
|
表 2 各估计方法对比分析 Tab. 2 The estimation methods comparison and analysis |
由表 2可知,随着沉降观测期数的增加,各模型a、b的预测值逐渐靠近真值,后验比逐渐减小。当用前7期数据建立模型时,PEIV-TLS模型预测效果最差,后验比达到0.738。随着建模期数的增加,PEIV-TLS模型预测精度快速提高,在第10期时,预测精度靠近PEIV-TLS-IGGⅢ模型。这也验证了本文模拟实验的结论——PEIV-TLS模型受观测数据误差大小和分布规律的影响较大,预测值不稳定。LS-IGGⅢ模型预测值比较稳定,但是随着建模期数的增加,LS-IGGⅢ模型预测精度还是很低,后验比最大,主要是因为LS-IGGⅢ没有进行系数矩阵误差改正。而PEIV-TLS-IGGⅢ模型的后验比最小,预测精度最高。
综上可知,PEIV-TLS-IGGⅢ模型加入了IGGⅢ抗差方案,具有一定的抗差性,稳定性优于PEIV-TLS模型。同时,PEIV-TLS-IGGⅢ模型使用了总体最小二乘准则,考虑了系数矩阵误差改正,因此预测精度高于LS-IGGⅢ模型。
4 结语1) 通过模拟实验可以得出,当观测数据中含有粗差时,LS估计和PEIV-TLS估计都对粗差很敏感,不具备抗差性。PEIV-TLS因为考虑了系数矩阵的误差,其估计精度高于LS估计,但PEIV-TLS模型估计值方差较大,预测不稳定。
2) 由工程实例可知,PEIV-TLS-IGGⅢ模型考虑了系数矩阵误差,并在总体最小二乘条件下求解未知参数,预测精度高于LS-IGGⅢ模型。同时,PEIV-TLS-IGGⅢ模型具有一定的抗差性,预测值稳定性高于PEIV-TLS模型。
3) 高铁路基前期下沉量大,下沉速度快,容易产生测量误差,并且前期的测量值对后期的沉降预测影响较大。而PEIV-TLS-IGGⅢ方法使用少量数据就能实现高精度预测,为迅速准确预测工后沉降量、确定何时开始轨道工程施工提供依据。
本文算法虽然考虑了灰色白化微分方程系数矩阵常数项无需改正,但无法保证系数矩阵B中常数项拥有相同的改正数。因此,如何提高预测精度,仍需进一步研究。实际工程中,观测数据受白噪声、系统误差等多种类型误差的影响,如何对误差进行分类和改正也需进一步研究。
| [1] |
伍绍浩. 基于稳健估计的高速铁路沉降预测与数据处理方法研究[D]. 长沙: 中南大学, 2014 (Wu Shaohao. Research of Settlement Prediction and Data Processing Based on Robust Estimation on High-Speed Railway Underline Construction[D]. Changsha: Central South University, 2014) http://cdmd.cnki.com.cn/Article/CDMD-10533-1014408576.htm
(  0) 0) |
| [2] |
岳建平, 田林亚. 变形监测技术与应用[M]. 北京: 国防工业出版社, 2014 (Yue Jianping, Tian Linya. Deformation Monitoring Technology and Application[M]. Beijing: National Defense Industry Press, 2014)
(  0) 0) |
| [3] |
铁道部工程管理中心. 客运专线铁路变形观测评估技术手册[M]. 北京: 铁道出版社, 2011 (The Ministry of Railways Engineering Management Center. Passenger Dedicated Railway Deformation Observation Technical Manuals[M]. Beijing: Railway Publishing House, 2011)
(  0) 0) |
| [4] |
邓聚龙. 灰理论基础[M]. 武汉: 华中科技大学出版社, 2002 (Deng Julong. Grey Theory[M]. Wuhan: Huazhong University of Science and Technology Press, 2002)
(  0) 0) |
| [5] |
Xu P L. The Effect of Errors-in-Variables on Variance Component Estimation[J]. Journal of Geodesy, 2016, 90(8): 1-21
(  0) 0) |
| [6] |
鲁铁定. 总体最小二乘平差理论及其在测绘数据处理中的应用[D]. 武汉: 武汉大学, 2010 (Lu Tieding. The Total Least Squares Adjustment Theoryand Its Applications in Surveying and Mapping Data Processing[D]. Wuhan: Wuhan University, 2010) http://kns.cnki.net/KCMS/detail/detail.aspx?filename=chxb201304028&dbname=CJFD&dbcode=CJFQ
(  0) 0) |
| [7] |
曾文宪. 系数矩阵误差对EIV模型平差结果的影响研究[D]. 武汉: 武汉大学, 2013 (Zeng Wenxian. Effect of the Random Design Matrix on Adjustment of an EIV Model and Its Reliability Theory[D]. Wuhan: Wuhan University, 2013) http://cdmd.cnki.com.cn/Article/CDMD-10486-1013210882.htm
(  0) 0) |
| [8] |
陈义, 陆珏. 以三维坐标转换为例解算稳健总体最小二乘方法[J]. 测绘学报, 2012, 41(5): 715-722 (Chen Yi, Lu Jue. Performing 3D Similarity Transformation by Robust Total Least Squares[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 715-722)
(  0) 0) |
| [9] |
刘亚彬, 郑南山, 张旭, 等. GPS高程拟合的加权总体最小二乘抗差估计[J]. 大地测量与地球动力学, 2016, 36(1): 30-34 (Liu Yabin, Zheng Nanshan, Zhang Xu, et al. Robust Weighed Total Least Squares Estimation for GPS Leveling Fitting[J]. Journal of Geodesy and Geodynamics, 2016, 36(1): 30-34)
(  0) 0) |
| [10] |
龚循强, 李志林. 稳健加权总体最小二乘法[J]. 测绘学报, 2014, 43(9): 888-894 (Gong Xunqiang, Li Zhilin. Robust Weighted Total Least Squares Method[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(9): 888-894)
(  0) 0) |
2. School of Geodesy and Geomatics, Wuhan University, 129 Luoyu Road, Wuhan 430079, China;
3. Key Laboratory for Digital Land and Resources of Jiangxi Province, East China University of Technology, 418 Guanglan Road, Nanchang 330013, China
 2018, Vol. 38
2018, Vol. 38


