测量工作者能从测量目标区域获得第一手数据资料[1],但测量数据中往往包含许多不确定的先验信息或附加信息(其统计信息和概率分布函数无法确定)[2-3],建立的函数模型常出现病态现象[4]。王乐洋等[5]、曾文宪等[6]运用整体最小二乘的平差方法处理此类病态问题,但考虑到整体最小二乘平差模型将不确定性同时融入观测矩阵和系数矩阵,可能导致系数矩阵过度修正[7]。另有学者将先验信息转化成等式或者不等式约束,应用于GPS、导航以及变形监测模型的建立[8-12]。等式和不等式约束虽然可以更好地描述观测对象的几何和物理力学性质,容易建立相关的约束平差模型,但对于一些以范围、集合形式出现的复杂先验信息也无能为力。本文通过研究边坡变形非线性时变系统的力学原理,利用多项式拟合方法改进原模型,使之适用于测量工作者普遍接受的高斯-马尔科夫平差模型,且在参数解算过程中考虑测量数据的不确定性给解算结果带来消极影响,通过限制不确定度,利用min-max准则提高参数解算的准确性。最后将预测结果与实测数据进行对比,分析改进的边坡变形非线性时变系统预测变形的有效性。
1 改进的高边坡变形非线性时变系统 1.1 时效因素和降雨因素边坡变形是内外动力因素共同作用下的外在表现。高边坡挖掘引起的变形可分为浅层改造变形和时效变形,其中随时间持续发展的时效变形为高边坡变形失稳的主要表现。有学者通过大量的室内实验和现场观察资料,总结变形与控制因素(时间、应力、稳定等)之间的函数关系[13-15],建立了边坡变形的经验或半经验模型,供预测边坡失稳破坏的可能性。按照函数形式,岩石经验蠕变公式分为以下3种类型。
1) 幂函数型, 表达式为:
| $ y\left( t \right) = c{t^d} $ | (1) |
2) 对数函数型,表达式为:
| $ y\left( t \right) = u + v\ln \left( t \right) $ | (2) |
3) 指数函数型,表达式为:
| $ y\left( t \right) = q\left( {1 - {{\rm{e}}^{f\left( t \right)}}} \right) $ | (3) |
岩石流变可分为3个阶段:初始流变阶段(在此阶段,岩石流变速率很快衰减为一个不为0的恒定值)、稳态流变阶段(在此阶段,岩石流变速率基本保持不变)、加速流变阶段(在此阶段,岩石流变速率迅速增大,直至破裂)。前两个阶段可以采用式(2)拟合;加速流变阶段采用式(1)拟合,充分反映加速流变特性。根据室内流变实验结果,可拟定边坡变形的时效特性模型为:
| $ {y_\xi }\left( t \right) = u + v\ln \left( t \right) + c{t^d} $ | (4) |
式中,yξ(t)为边坡时效变形,t为时间间隔(监测开始的累计天数),u、v、c、d为时效特性系数。
降雨是除了时效特性以外影响边坡变形的另一个主要的外动力因素。由于降雨对边坡的影响相对复杂, 许强等[13]提出采用有效降雨量进行处理,具体做法为:将选取观测日期前一个月的降雨量与间隔天数乘以0.8进行折减,然后累计求和,即得到降雨因子P:
| $ P = \sum\limits_{i = 0}^{T - 1} {{{0.8}^i}{R_i}} $ | (5) |
| $ {y_P}\left( t \right) = r\sum\limits_{i = 0}^{T - 1} {{{0.8}^i}{R_i}} $ | (6) |
式中,T为观测当月天数,Ri为距离观测第i天的降雨量,r为降雨因子系数。
综合时效因素和降雨因素,可以得到边坡变形的非线性时变模型:
| $ \tilde y = {y_\xi }\left( t \right) + {y_P}\left( t \right) = u + v\ln \left( t \right) + c{t^d} + rP $ | (7) |
式中,u、v、c、d、r为常数,
在MATLAB平台上能用非线性回归的方法求解式(7)中的5个常数。本文通过观察岩石流变速率图以及实测位移量月变化图,决定采用多项式拟合的方法改进式(7)中的幂函数部分,多项式最高次数选择为二次(通过实验发现,二次多项式拟合结果优于其他高次多项式),既能反映位移变化的非线性,同时计算量也较小。另外,改进后模型的未知参数全部剥离于输入数据(时间间隔t、降雨因子P),运用间接平差同样能求解出相应的系数,但运算步骤更为简单,使用方便。
改进模型如下。令
| $ c{t^d} = mt + n{t^2} $ | (8) |
于是得到改进的边坡变形非线性时变系统:
| $ \tilde y = {y_\xi }\left( t \right) + {y_P}\left( t \right) = u + v\ln \left( t \right) + mt + n{t^2} + rP $ | (9) |
为了方便理解和计算,令
| $ \mathit{\boldsymbol{L}} = \mathit{\boldsymbol{y}} $ |
| $ \mathit{\boldsymbol{X}} = {\left( {\begin{array}{*{20}{c}} r&n&m&v&u \end{array}} \right)^{\rm{T}}} $ |
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {{P_1}}&{t_1^2}&{{t_1}}&{\ln \left( {{t_1}} \right)}&1\\ {{P_2}}&{t_2^2}&{{t_2}}&{\ln \left( {{t_2}} \right)}&1\\ \vdots&\vdots&\vdots&\vdots&\vdots \\ {{P_n}}&{t_n^2}&{{t_n}}&{\ln \left( {{t_n}} \right)}&1 \end{array}} \right] $ |
由间接平差公式可得:
| $ \mathit{\boldsymbol{\hat X}} = {\mathit{\boldsymbol{N}}^{ - 1}}\mathit{\boldsymbol{c}}\left( {\mathit{\boldsymbol{N}} = {\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B}},\mathit{\boldsymbol{c}} = {\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{L}}} \right) $ |
观测数据常常存在一些不确定的附加信息或先验信息,它们的统计信息和概率分布函数无法确定。例如对于某一次沉降观测值xi,其干扰量Δxi带有不确定区间,即
| $ {a_i} \le \Delta {x_i} \le {b_i},i = 1,2, \cdots ,n $ |
而上一节所介绍的非线性时变模型中,边坡变形位移和有效降雨量类似沉降观测值,具备不确定区间的干扰量,于是B、L的干扰量ΔB、ΔL就是带有不确定性的矩阵和向量,可以用2-范数形式表达这种不确定性:
| $ {\left\| {\Delta \mathit{\boldsymbol{B}}} \right\|_2} \le \alpha ,{\left\| {\Delta \mathit{\boldsymbol{L}}} \right\|_2} \le \beta $ | (10) |
在平差模型中融入不确定度参数α和β,于是成为带不确定性的平差模型:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{L}} + \Delta \mathit{\boldsymbol{L}} = \left( {\mathit{\boldsymbol{B}} + \Delta \mathit{\boldsymbol{B}}} \right)\mathit{\boldsymbol{X}}\\ {\left\| {\Delta \mathit{\boldsymbol{B}}} \right\|_2} \le \alpha ,{\left\| {\Delta \mathit{\boldsymbol{L}}} \right\|_2} \le \beta \end{array} \right. $ | (11) |
在带不确定性的平差模型中,不确定度α和β的上限已知,即系数矩阵B和观测向量L的不确定性是已知的。而我们知道,在整体最小二乘平差(TLS)中,系数矩阵和观测向量的不确定性是未知的;最小二乘平差(LS)中没有系数矩阵的不确定性(即ΔB=0),观测向量的不确定性未知。
对ΔB和ΔL的不确定性进行参数估计,可根据文献[3]给出的min-max平差准则,让残差的最大不确定性达到最小,即
| $ \begin{array}{l} \mathop {\min }\limits_{\hat X} \mathop {\max }\limits_{{{\left\| {\Delta \mathit{\boldsymbol{B}}} \right\|}_2} \le \alpha ,{{\left\| {\Delta \mathit{\boldsymbol{L}}} \right\|}_2} \le \beta } \\ \left\{ {{{\left\| {\left( {\mathit{\boldsymbol{L}} + \Delta \mathit{\boldsymbol{L}}} \right) - \left( {\mathit{\boldsymbol{B}} + \Delta \mathit{\boldsymbol{B}}} \right)\mathit{\boldsymbol{\hat X}}} \right\|}_2}} \right\} \end{array} $ | (12) |
在此准则下的一个岭估计为:
| $ \mathit{\boldsymbol{\hat X}} = {\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B}} + \mu \mathit{\boldsymbol{I}}} \right)^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{L}} $ | (13) |
岭参数μ的计算方法见文献[3]。
3 实例分析选取某水电站左岸边坡累计变形最大、变形速率最快的变形点TP12-1和TP12-5的位移观测数据进行分析(如表 1、图 1)。利用前20期数据(2005-12~2007-07)建立改进的边坡变形非线性时变模型,分别运用最小二乘法(LS)、整体最小二乘法(TLS)以及带不确定性的平差算法(ULS)(关于α、β的选取,根据每年有效降雨量与平均年有效降雨量之间的差值在6 mm内,确定月有效降雨量的不确定度为0.5 mm,从而得到‖ΔB‖2≤α=2.5,位移的不确定性受到观测手段、仪器精度等影响,按一级变形监测精度要求,取位移不确定度为1 mm,得到‖ΔL‖2≤β=5)计算模型中的5个参数u、v、c、d、r,然后根据所计算的参数以及后7期(2007-08~2008-02)观测数据预测相应的边坡位移量,将预测值与实测边坡位移量进行比较,分析不确定平差算法在改进的边坡变形非线性时变系统中的有效性。
|
|
表 1 变形点TP12-1和TP12-5的位移观测数据 Tab. 1 Displacement observation data of point TP12-1 and point TP12-5 |

|
图 1 变形点TP12-1和TP12-5的位移量 Fig. 1 Displacement values of point TP12-1 and point TP12-5 |
从表 2、表 3计算结果看出,对于变形点TP12-1和TP12-5,3种平差模型的预测结果都能反映实际边坡变形的趋势。计算3种模型预测绝对误差绝对值的平均值,TP12-1结果分别为2.86 mm(LS)、3.02 mm(TLS)和0.92 mm(ULS);TP12-5结果分别为0.56 mm(LS)、2.17 mm(TLS)和0.40 mm(ULS)。说明ULS预测结果更接近实际测量数据,TLS由于系数矩阵和观测向量同时考虑不确定性,但这种不确定性的限度未知,导致修正过度,使得结果不及LS。而对于变形点TP12-5,可能由于不确定性对于该点测量数据影响较小,所以ULS预测结果和LS预测结果相差不大。通过图 2和图 3可以直观地看到,ULS算法结果曲线更接近实测曲线,与上述结论一致。
|
|
表 2 LS、TLS和ULS的预测结果以及绝对误差(TP12-1) Tab. 2 Forecasted results and absolute errors of LS, TLS and ULS(TP12-1) |
|
|
表 3 LS、TLS和ULS的预测结果以及绝对误差(TP12-5) Tab. 3 Forecasted results and absolute errors of LS, TLS and ULS(TP12-5) |
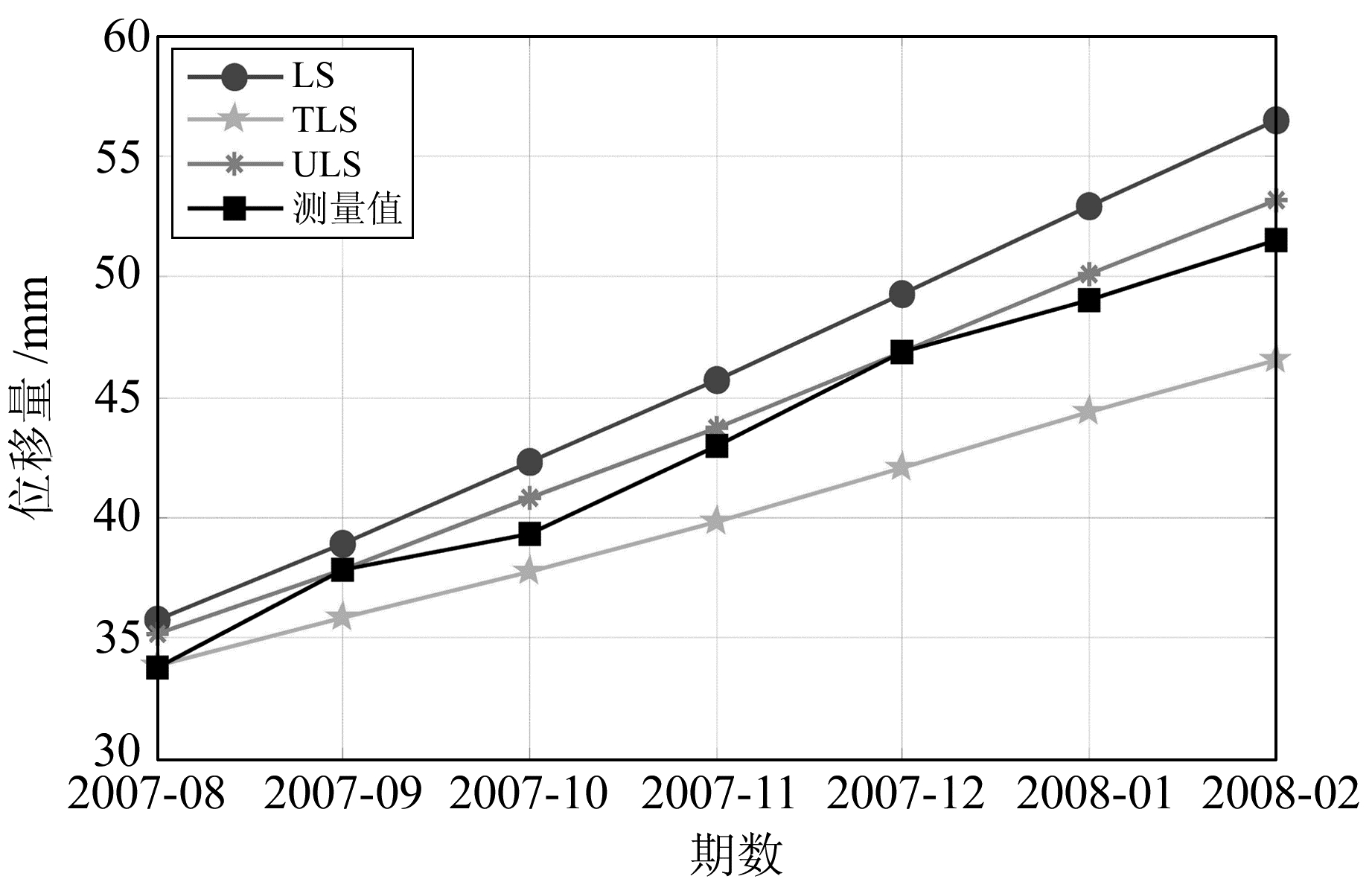
|
图 2 预测曲线与实测曲线(TP12-1) Fig. 2 Line of forecasted results and observation data(TP12-1) |
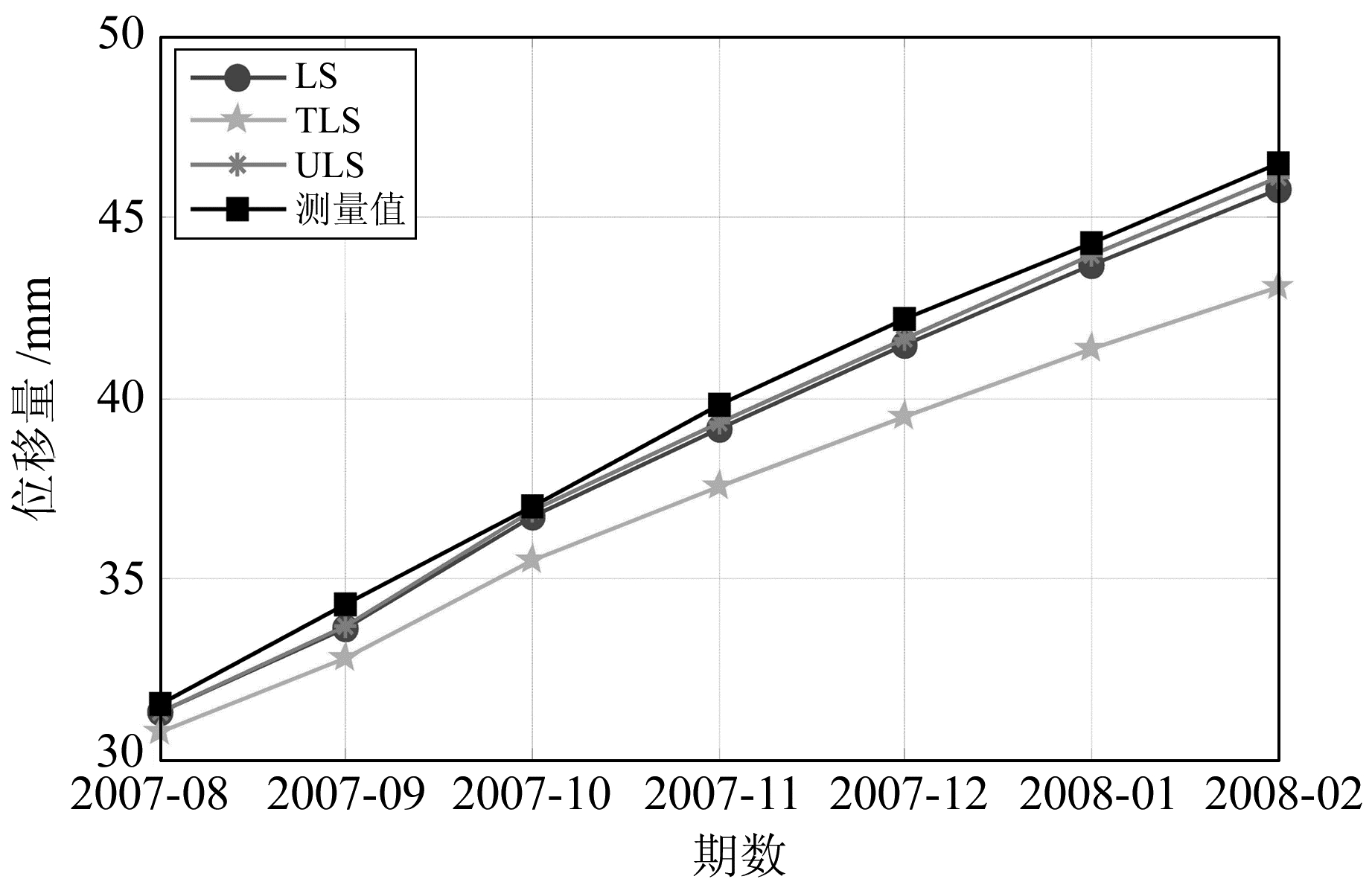
|
图 3 预测曲线与实测曲线(TP12-5) Fig. 3 Line of forecasted results and observation data(TP12-5) |
边坡变形非线性时变系统对边坡变形预测及其安全性判定有重要研究意义。本文通过研究该系统的力学原理,利用多项式拟合方法改进原模型,使之适用于测量工作者普遍接受的高斯-马尔科夫平差模型,且在参数解算过程中,考虑到测量数据的不确定性给解算结果带来的消极影响,提出带不确定性的平差算法(ULS)。将不确定度融入模型系数矩阵和观测向量,分别加以限制约束,利用min-max准则,结合残差中不确定性的误差传播规律,避免了整体最小二乘平差(TLS)虽然考虑不确定性但不确定性未知导致的模型修正过度,使得参数估计结果不佳的弊端。实测数据的预测结果证明了改进的边坡变形非线性时变系统预测变形的有效性。
| [1] |
贾明娟, 牛冲. 基于灰色模型的建筑物沉降预测研究[J]. 测绘与空间地理信息, 2016, 39(1): 44-46 (Jia Mingjuan, Niu Chong. Research on Building Subsidence Prediction Based on Gray Model[J]. Geomatics & Spatial Information Technology, 2016, 39(1): 44-46)
(  0) 0) |
| [2] |
宋迎春, 谢雪梅, 陈晓林. 不确定性平差模型的平差准则与解算方法[J]. 测绘学报, 2015, 44(2): 135-141 (Song Yingchun, Xie Xuemei, Chen Xiaolin. Adjustment Criterion and Algorithm in Adjustment Model with Uncertainty[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 135-141 DOI:10.11947/j.AGCS.2015.20130213)
(  0) 0) |
| [3] |
宋迎春, 金昊, 崔先强. 带有不确定性的观测数据平差解算方法[J]. 武汉大学学报:信息科学版, 2014, 39(7): 788-792 (Song Yingchun, Jin Hao, Cui Xianqiang. Adjustment Algorithm about Observation Data with Uncertainty[J]. Geomatics and Information Science of Wuhan University, 2014, 39(7): 788-792)
(  0) 0) |
| [4] |
谢建, 朱建军. 等式约束病态模型的正则化解及其统计性质[J]. 武汉大学学报:信息科学版, 2013, 38(12): 1440-1444 (Xie Jian, Zhu Jianjun. A Regularized Solution and Statistical Properties of Ill-Posed Problem with Equality Constraints[J]. Geomatics and Information Science of Wuhan University, 2013, 38(12): 1440-1444)
(  0) 0) |
| [5] |
王乐洋, 于冬冬. 病态总体最小二乘问题的虚拟观测解法[J]. 测绘学报, 2014, 43(6): 575-581 (Wang Leyang, Yu Dongdong. Virtual Observation Method to Ill-Posed Total Least Squares Problem[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(6): 575-581)
(  0) 0) |
| [6] |
曾文宪, 方兴, 刘经南, 等. 附有不等式约束的加权整体最小二乘算法[J]. 测绘学报, 2014, 43(10): 1013-1018 (Zeng Wenxian, Fang Xing, Liu Jingnan, et al. Weighted Total Least Squares Algorithm with Inequality Constraints[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10): 1013-1018)
(  0) 0) |
| [7] |
邹渤, 宋迎春, 唐争气, 等. 沉降观测AR模型的不确定性平差算法[J]. 大地测量与地球动力学, 2016, 36(8): 686-688 (Zou Bo, Song Yingchun, Tang Zhengqi, et al. Adjustment Alorithm on AR Model with Uncertain in Settlement Observation[J]. Journal of Geodesy and Geodynamics, 2016, 36(8): 686-688)
(  0) 0) |
| [8] |
谢建, 朱建军. 等式约束对病态问题的影响及约束正则化方法[J]. 武汉大学学报:信息科学版, 2015, 40(10): 1344-1348 (Xie Jian, Zhu Jianjun. Influence of Equality Constraints on Ill-Conditioned Problems and Constrained Regularization Method[J]. Geomatics and Information Science of Wuhan University, 2015, 40(10): 1344-1348)
(  0) 0) |
| [9] |
王乐洋, 朱建军. 附不等式约束的大地测量反演[J]. 大地测量与地球动力学, 2008, 28(1): 109-113 (Wang Leyang, Zhu Jianjun. Geodetic Inversion Theory Constrained with Inequality[J]. Journal of Geodesy and Geodynamics, 2008, 28(1): 109-113)
(  0) 0) |
| [10] |
王乐洋, 许才军, 汪建军. 附有病态约束矩阵的等式约束反演问题研究[J]. 测绘学报, 2009, 38(5): 397-401 (Wang Leyang, Xu Caijun, Wang Jianjun. Research on Equality Constraint Inversion with Ill-Posed Constraint Matrix[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(5): 397-401)
(  0) 0) |
| [11] |
冯光财, 朱建军. 基于有效约束的附不等式约束平差的一种新算法[J]. 测绘学报, 2007, 36(2): 119-122 (Feng Guangcai, Zhu Jianjun. A New Approach to Inequality Constrained Least-Squares Adjustment[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 119-122)
(  0) 0) |
| [12] |
张松林, 陈德虎. 带不等式约束的间接平差模型的3种解算方法比较[J]. 大地测量与地球动力学, 2013, 33(2): 41-44 (Zhang Songlin, Chen Dehu. Comparson among Three Algorithms of Parameter Adjustment Model with Inequality Constraints[J]. Journal of Geodesy and Geodynamics, 2013, 33(2): 41-44)
(  0) 0) |
| [13] |
许强, 汤明高, 徐开祥, 等. 滑坡时空演化规律及预警预报研究[J]. 岩石力学与工程学报, 2008, 27(6): 1104-1112 (Xu Qiang, Tang Minggao, Xu Kaixiang, et al. Research on Space-Time Evolution Laws and Early Warning Prediction of Landslides[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(6): 1104-1112)
(  0) 0) |
| [14] |
谈小龙, 徐卫亚, 梁桂兰, 等. 高边坡变形非线性时变统计模型研究[J]. 岩土力学, 2010, 31(5): 1633-1650 (Tan Xiaolong, Xu Weiya, Liang Guilan, et al. Research on Nonlinear Time Series Evolution Statistic Model of High Slope Displacements[J]. Rock and Soil Mechanics, 2010, 31(5): 1633-1650)
(  0) 0) |
| [15] |
郑东健, 顾冲时, 吴中如. 边坡变形的多因素时变预测模型[J]. 岩石力学与工程学报, 2005, 24(17): 3180-3184 (Zheng Dongjian, Gu Chongshi, Wu Zhongru. Time Series Evolution Forecasting Model of Slope Deformation Based on Multiple Factors[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(17): 3180-3184 DOI:10.3321/j.issn:1000-6915.2005.17.028)
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38

