2. 武汉地震工程研究院有限公司,武汉市洪山侧路40号,430071
危岩是指位于陡崖或陡坡上被岩体结构面切割且稳定性较差的岩块,按照失稳模式可分为滑塌型、倾倒型和坠落型3类[1]。危岩是我国三峡库区和西部高山深谷区的公路边坡及斜坡带的主要地质灾害类型,具有分布面广、稳定性差、致灾严重等特点。危岩的防治需要系统地对危岩发育机理进行研究,其核心是研究主控结构面的形成及发展。将危岩体后部贯通或断续贯通且力学强度较低的面(或带)定义为主控结构面,危岩变形破坏过程本质上就是主控结构面扩展、相互作用和贯通的过程。结构面尖端在应力场和外界因素的作用下发生的失稳扩展是危岩致灾的根本原因,所以研究结构面尖端的断裂韧度、断裂机理、断裂判据对于认识危岩发育机理和采取有效防治措施都有重要意义。
近年来,断裂力学开始应用于岩土工程,解决了一些常规岩石力学无法解决的问题,尤其在岩体节理、裂隙断裂扩展等研究上取得了许多成果。邓华锋等[2]和韩铁林等[3]通过实验对砂岩的断裂韧度和强度特征进行研究,发现干湿循环和冻融循环对岩石的力学参数劣化程度影响非常显著。周家文等[4]建立了基于Mohr-Coulumb准则和Drucker-Prager准则的岩石压剪断裂判据。在对危岩体结构面的断裂机理研究方面,主要是以应力为参数,通过推导计算结构面尖端应力强度因子来解释主控结构面的扩展和评价危岩体的稳定性[5-6]。以能量为参数的能量释放率准则目前在危岩机理研究中暂时没有应用。
本文基于线弹性断裂力学能量释放率准则的假定,计算推导出剪切破坏型危岩的断裂扩展角和断裂韧度,为进一步从能量角度探究危岩的破坏机理提供一种思路。
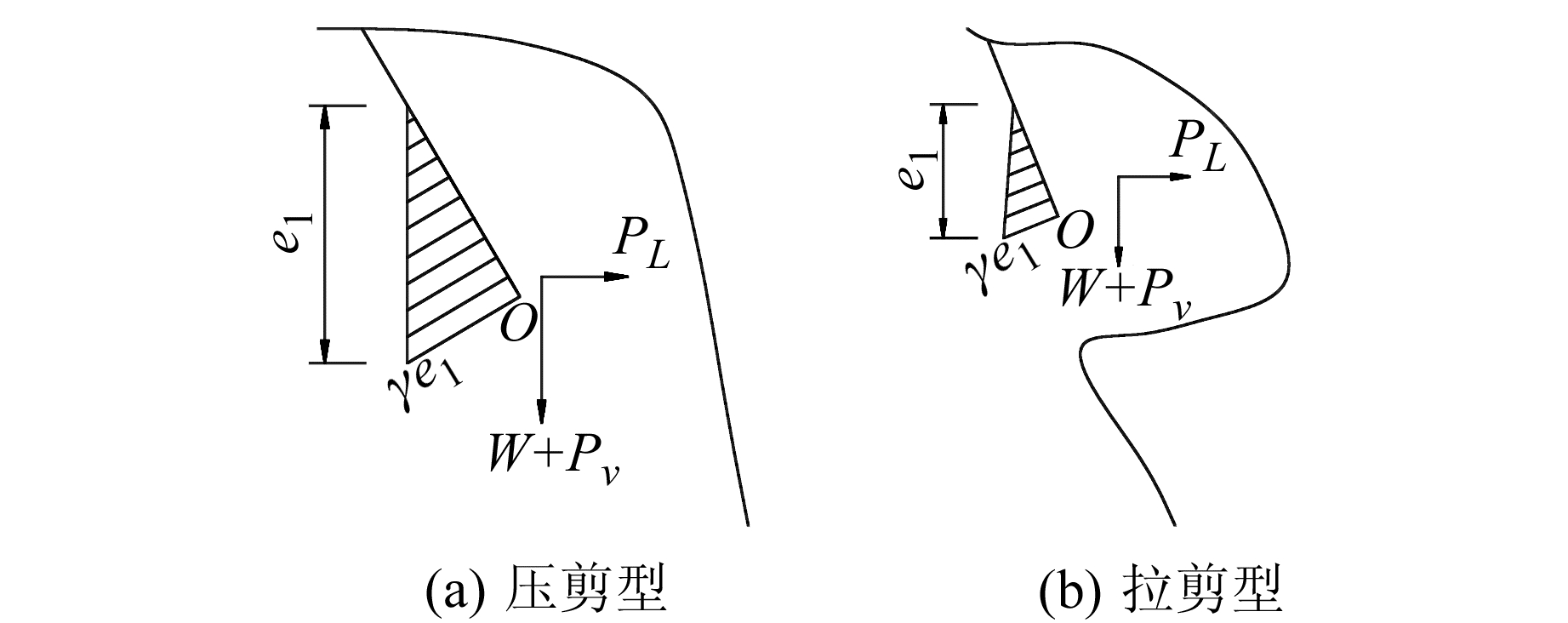
1 应力强度因子求解坠落型危岩属于主控结构面的拉裂破坏(Ⅰ型裂纹扩展问题);滑塌型危岩属于主控结构的压剪破坏(Ⅰ-Ⅱ复合型裂纹扩展问题);倾倒型危岩属于主控结构面的拉剪破坏(Ⅰ-Ⅱ复合型裂纹扩展问题)。根据现有资料统计,在危岩体集中分布的地区,以滑塌、倾倒破坏的剪切型危岩占危岩总数的70%以上,故本文以此为研究对象(图 1)。
|
图 1 剪切型危岩受力示意图 Fig. 1 The model of shear-type unstable rock |
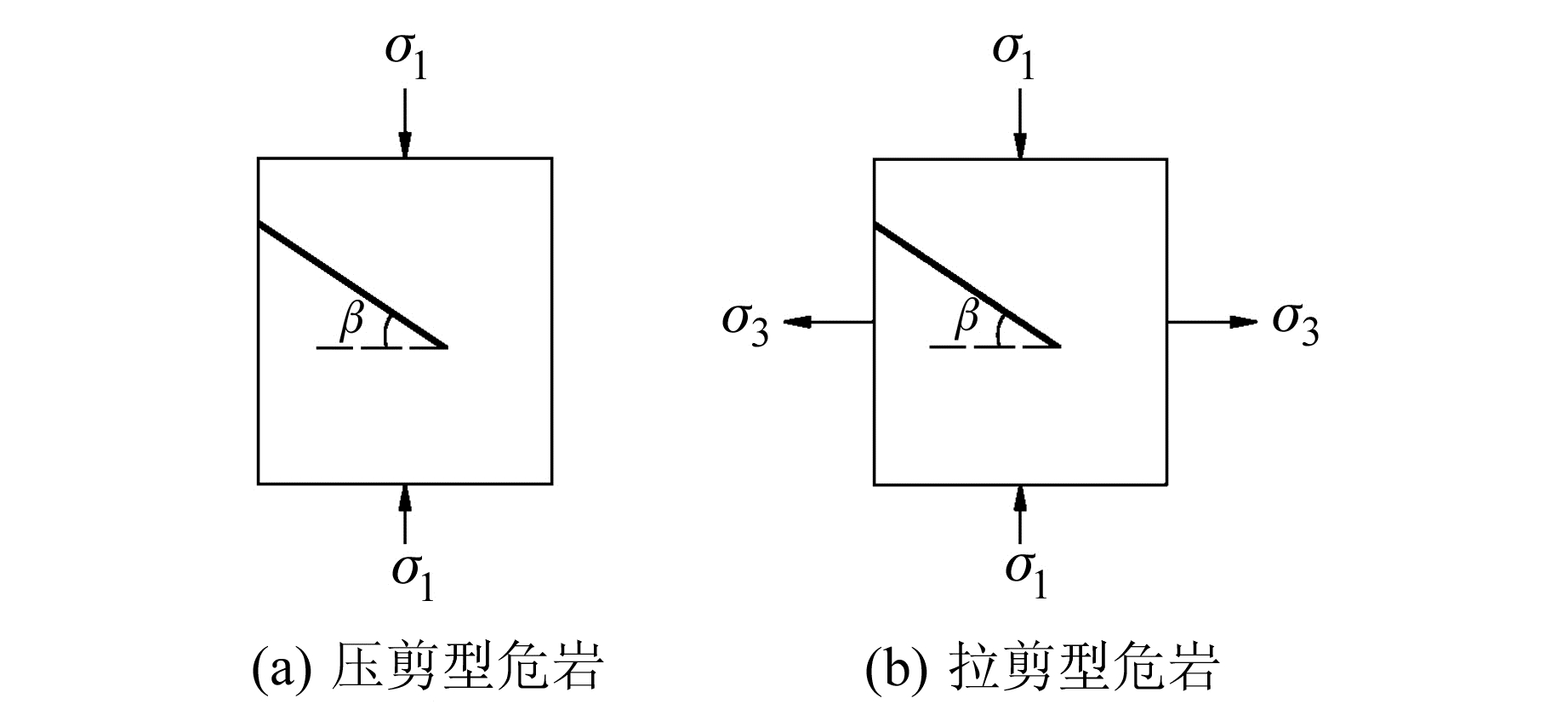
危岩体作用在主控结构面上的应力可归纳为图 2中两种基本形式[7-8]。
|
图 2 剪切型危岩主控结构面应力作用形式 Fig. 2 The stress on the control fissure of shear-type unstable rock |
图 2中,σ1为危岩体所受的竖向应力,由危岩体自重W、竖向地震力PV以及渗透力的竖向分量决定;σ3为危岩体水平向应力,由水平地震力PL和渗透力的水平分量决定(各变量如图 1所示)。
对于压剪型危岩(图 2(a)),主控结构面所受的正应力和切应力分别为:
| $ \sigma = - {\sigma _1}{\cos ^2}\beta + {\gamma _w}{e_1} $ | (1) |
| $ \tau = {\sigma _1}\sin \beta \cos \beta + \frac{1}{2}b{\gamma _w}\cos \beta $ | (2) |
式(1)右边的负号表示在压剪应力作用下,沿结构面方向不引起结构面的张开,而是使其闭合,减小了裂尖的应力强度因子,即压应力对结构面有增韧阻裂的作用;拉应力对结构面起拉张作用,增大裂尖的应力强度因子,故取为正号,下同。
对于拉剪型危岩(图 2(b)),主控结构面所受的正应力和切应力分别为:
| $ \sigma = \frac{1}{2}\left[ {\left( {{\sigma _1} - {\sigma _3}} \right) + \left( {{\sigma _1} + {\sigma _3}} \right)\cos 2\beta } \right] - {\gamma _w}{e_1} $ | (3) |
| $ \tau = \frac{1}{2}\left( {{\sigma _1} + {\sigma _3}} \right)\sin 2\beta + \frac{1}{2}b{\gamma _w}\cos \beta $ | (4) |
对于压剪型危岩,相应的Ⅰ、Ⅱ型应力强度因子为:
| $ \left\{ \begin{array}{l} {K_{\rm{I}}} = - \left( {{\sigma _1}{{\cos }^2}\beta - {\gamma _w}{e_1}} \right)\sqrt {\pi a} \\ {K_{{\rm{II}}}} = \left( {{\sigma _1}\sin \beta \cos \beta + \frac{1}{2}b{\gamma _w}\cos \beta } \right)\sqrt {\pi a} \end{array} \right. $ | (5) |
对于拉剪型危岩,相应的Ⅰ、Ⅱ型应力强度因子为:
| $ \left\{ \begin{array}{l} {K_{\rm{I}}} = - \left\{ {\frac{1}{2}\left[ {\left( {{\sigma _1} - {\sigma _3}} \right) + } \right.} \right.\\ \;\;\;\;\left. {\left. {\left( {{\sigma _1} + {\sigma _3}} \right)\cos 2\beta } \right] - {\gamma _w}{e_1}} \right\}\sqrt {\pi a} \\ {K_{{\rm{II}}}} = \left[ {\frac{1}{2}\left( {{\sigma _1} + {\sigma _3}} \right)\sin 2\beta + } \right.\\ \;\;\;\;\;\left. {\frac{1}{2}b{\gamma _w}\cos \beta } \right]\sqrt {\pi a} \end{array} \right. $ | (6) |
式中,γw为水的重度,e1为主控结构面贯通段内的充水高度,β为结构面倾角,a为结构面的长度,b为结构面开度。
2 能量释放率判据对于主控结构面属于Ⅰ-Ⅱ复合型裂纹的压剪和拉剪型危岩,断裂扩展并不按原裂纹面方向进行。按应变能释放率准则,假设[9-10]:
1) 裂纹沿着应变能释放率达到最大的方向扩展,即
| $ \frac{{\partial {G_\theta }}}{{\partial \theta }} = 0 $ | (7) |
由式(7)可求得开裂角θ=θ0。
2) 当该方向(θ=θ0)上的应变能释放率达到临界值时(即断裂韧度),裂纹开始扩展,即
| $ {G_{{\theta _0}}} = {G_\theta }\left| {_{\theta = {\theta _0}}} \right. = {G_{{\rm{IC}}}} $ | (8) |
对于剪切型危岩,视为平面应变情况,沿原裂纹方向扩展的能量释放率为:
| $ G = \frac{{\left( {1 - {\nu ^2}} \right)}}{E}\left( {K_{\rm{I}}^2 + K_{{\rm{II}}}^2} \right) $ | (9) |
式中,ν为泊松比,E为弹性模量。
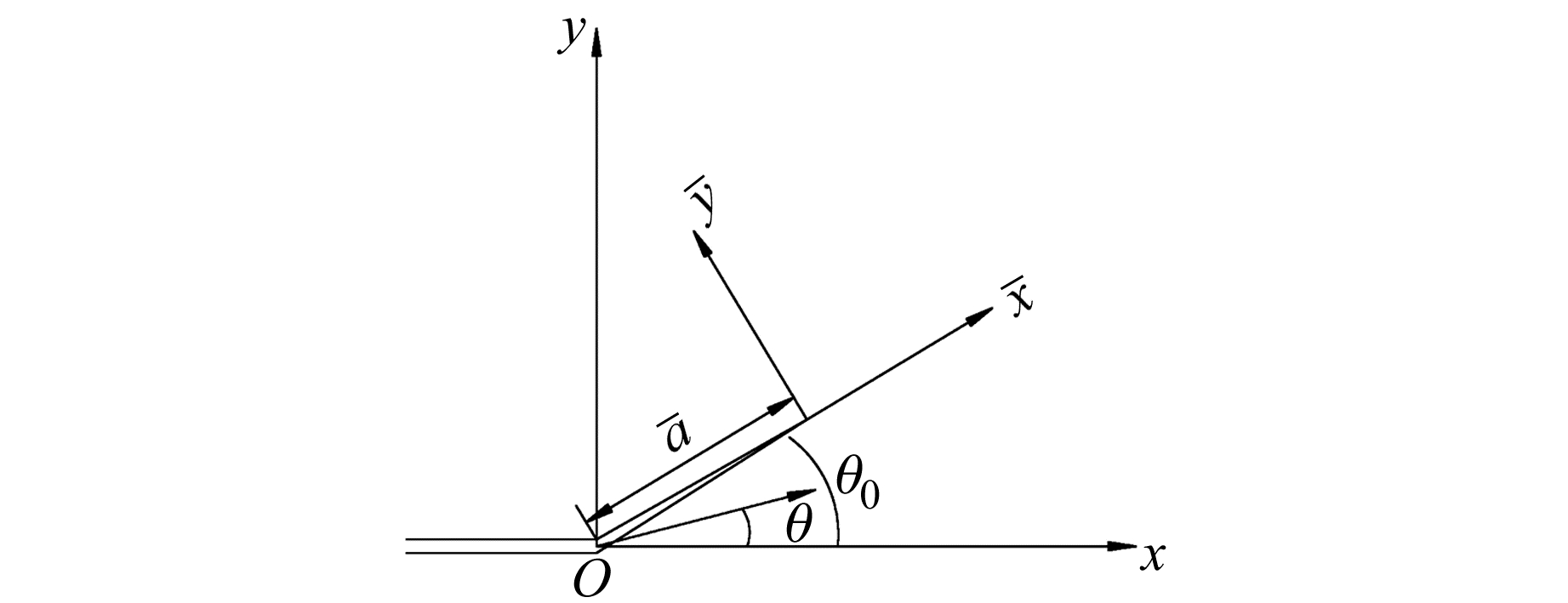
假设裂纹沿θ=θ0方向产生一个长为a的支裂纹(图 3),为了区别,将支裂纹的有关各量符号上加一横线。由于断裂的起始扩展条件是重点,不妨令a→0,利用连续性假设求应力强度因子的起始值KⅠ和KⅡ:
| $ \left\{ \begin{array}{l} {{\bar K}_{\rm{I}}} = \frac{1}{2}\cos \frac{{{\theta _0}}}{2}\left[ {{K_{\rm{I}}}\left( {1 + \cos {\theta _0}} \right) - 3{K_{{\rm{II}}}}\sin {\theta _0}} \right]\\ {{\bar K}_{{\rm{II}}}} = \frac{1}{2}\cos \frac{{{\theta _0}}}{2}\left[ {{K_{\rm{I}}}\sin {\theta _0} - {K_{{\rm{II}}}}\left( {3\cos {\theta _0} - 1} \right)} \right] \end{array} \right. $ | (10) |
|
图 3 结构面的扩展角及坐标系 Fig. 3 Cracking angle and coordinate system of fissure |
则主控结构面尖端开始扩展瞬间的能量释放率为:
| $ {G_{{\theta _0}}} = \frac{{\left( {1 - {\nu ^2}} \right)}}{E}\left( {\bar K_{\rm{I}}^2 + \bar K_{{\rm{II}}}^2} \right) $ | (11) |
将得到的开裂角θ0代入能量释放率准则的第2假设(式(8)),即可求得主控结构面失稳扩展的临界条件。
当能量释放率达到某临界值GIC时,裂纹开始扩展。将式(10)代入式(11),可得:
| $ \begin{array}{*{20}{c}} {{G_\theta } = \frac{{\left( {1 - {\nu ^2}} \right)}}{{4E}}\left( {1 + \cos {\theta _0}} \right)\left[ {K_{\rm{I}}^2\left( {1 + \cos \theta } \right) - } \right.}\\ {\left. {4{K_{\rm{I}}}{K_{{\rm{II}}}}\sin \theta + K_{{\rm{II}}}^2\left( {5 - 3\cos \theta } \right)} \right]} \end{array} $ | (12) |
联立式(7)和式(12),可由式(13)确定θ0:
| $ \begin{array}{*{20}{c}} {K_{\rm{I}}^2\sin \theta + {K_{\rm{I}}}{K_{{\rm{II}}}}\cos \theta + }\\ {{K_{\rm{I}}}{K_{{\rm{II}}}}\cos 2\theta - K_{{\rm{II}}}^2\sin \theta = 0} \end{array} $ | (13) |
对式(13)进行变量替换,令
| $ {\lambda ^2}{t^4} - {t^3} + 3\lambda {t^2} + {\lambda ^2}t - t - \lambda = 0 $ | (14) |
取不同的λ值,都有与之相对应的开裂角θ0。将求得的θ0代入式(12)中,即可求得主控结构面扩展时的能量释放率。
对于压剪、拉剪型危岩,将式(5)、式(6)分别代入式(12)、式(13)中,即得到以β为参数确定的GIC和θ0。
3 算例首立山危岩位于重庆市万州区天城经济开发区,危岩发育在首立山的陡崖上(图 4(a))。陡崖坡脚多为泥岩,由于差异风化,与上部陡崖的砂岩形成岩腔,岩腔高1.0~3.0 m,深0.5~3.0 m(图 4(b))。陡崖裂隙发育,砂岩受裂隙切割破坏,共发育危岩体(带)145处,分布在高程195.0~425.6 m范围,体积在2.29~7 904.82 m3之间。危岩体顶端距陡崖坡脚的高度一般小于25 m,以中位危岩居多,低位危岩相对较少,严重威胁陡崖下的厂矿企业及居民区安全。

|
图 4 首立山危岩(中段)和差异风化形成的岩腔 Fig. 4 The middle section of Shoulishan unstable rocks and a rock cavity formed by differential weathering |
危岩体主要由砂岩构成,主要矿物成分为长石、石英,其余为云母等。天然块体密度平均值为2.51 g/cm3,饱和块体密度平均值为2.53 g/cm3,天然、饱和抗拉强度标准值分别为2.67 MPa、1.73 MPa,天然弹性模量为0.69×104 MPa,泊松比为0.21,饱和弹性模量为0.57×104 MPa,泊松比为0.23。从首立山危岩选取5个较为典型的剪切破坏型危岩体,计算天然状态下主控结构面开裂角θ0及断裂韧度GIC。
算例表明,以能量释放率准则建立的断裂判据可以用于危岩主控结构面断裂扩展的定量计算,断裂角的计算结果与基于最大周向应力准则的断裂角计算结果一致,主控结构面的开裂方向均是指向临空面方向。从计算过程来看,当岩体的材料参数一定时,结构面扩展的能量释放率和断裂后的扩展路径完全决定于其尖端应力场。
|
|
表 1 首立山典型剪切型危岩主控结构面开裂角计算结果 Tab. 1 The control fissure of typical shear-type unstable rocks cracking angle in Shoulishan |
除拉裂坠落型危岩外,其余类型的危岩属于剪切型危岩,其主控结构面的开裂扩展本质上是Ⅰ-Ⅱ复合型断裂问题。本文基于能量释放率准则的两点假设,推导出危岩主控结构面开裂角θ0及其断裂韧度GIC的计算公式,为从能量角度研究危岩发育机理提供了一种思路。以首立山典型剪切型危岩为例,得到了主控结构面的断裂韧度,基于能量释放率准则计算的危岩主控结构面扩展起始方向与最大周向应力准则推测方向一致。随着主控结构面的扩展,危岩总体表现出断裂韧度减小、危险性增大的趋势。
岩石作为一种非常复杂的固体脆性材料,各向异性特点显著,理论的推导和计算是建立在简化的力学模型基础上,与危岩体实际发育过程有着不小的差异。断裂的过程也是能量积累-扩展释放-再积累的过程,每一次扩展都会改变结构面尖端的应力状态,进而决定下一次扩展的能量释放率与扩展路径。准确地获取计算参数,建立可靠的结构面受力模型,是采用能量法进行危岩机理研究的难点。
| [1] |
陈洪凯, 唐红梅, 叶四桥. 危岩防治原理[M]. 北京: 地震出版社, 2006 (Chen Hongkai, Tang Hongmei, Ye Siqiao. Control Principle of Unstable Rocks[M]. Beijing: Seismological Press, 2006)
(  0) 0) |
| [2] |
邓华锋, 朱敏, 李建林, 等. 砂岩Ⅰ型断裂韧度及其与强度参数的相关性研究[J]. 岩土力学, 2012, 33(12): 3585-3591 (Deng Huafeng, Zhu Min, Li Jianlin, et al. Study of Mode-Ⅰ Fracture Toughness and Its Correlation with Strength Parameters of Sandstone[J]. Rock and Soil Mechanics, 2012, 33(12): 3585-3591)
(  0) 0) |
| [3] |
韩铁林, 师俊平, 陈蕴生. 冻融循环和干湿循环作用下砂岩断裂韧度及其与强度特征相关性的试验研究[J]. 固体力学学报, 2016, 37(4): 348-359 (Han Tielin, Shi Junping, Chen Yunsheng. Experimental Study on Fracture Toughness and Its Correlation with Strength Characteristics of Sandstone under Freeze-Thaw Cycles and Dry-Wet Cycles[J]. Chinese Journal of Solid Mechanics, 2016, 37(4): 348-359)
(  0) 0) |
| [4] |
周家文, 徐卫亚, 石崇. 基于破坏准则的岩石压剪断裂判据研究[J]. 岩石力学与工程学报, 2007, 26(6): 1194-1201 (Zhou Jiawen, Xu Weiya, Shi Chong. Investigation on Compression-Shear Fracture Criterion of Rock Based on Failure Criteria[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(6): 1194-1201)
(  0) 0) |
| [5] |
陈洪凯, 张祎. 考虑渗透力作用的危岩主控结构面断裂力学求解[J]. 重庆建筑大学学报, 2008, 30(5): 77-80 (Chen Hongkai, Zhang Yi. A Fracture Mechanics Solution for Control Fissure in Perilous Rock under Seepage Stress[J]. Journal of Chongqing Jianzhu University, 2008, 30(5): 77-80)
(  0) 0) |
| [6] |
周云涛. 三峡库区危岩稳定性断裂力学计算方法[J]. 岩土力学, 2016, 37(增1): 495-499 (Zhou Yuntao. A Method for Calculating the Stability of Unstable Rocks on Three Gorges Reservoir by Fracture Mechanics[J]. Rock and Soil Mechanics, 2016, 37(S1): 495-499)
(  0) 0) |
| [7] |
汤连生, 张鹏程, 王洋. 复合型裂纹的扩展规律[J]. 中山大学学报:自然科学版, 2003, 42(1): 90-94 (Tang Liansheng, Zhang Pengcheng, Wang Yang. Propagation of the Complex Cracks in Rocks without Water Pressure[J]. Acta Scientiarum Naturalium University Sunyatseni, 2003, 42(1): 90-94)
(  0) 0) |
| [8] |
Goodman R E. Introduction to Rock Mechanics[M]. New York: John Wiley & Sons Inc, 1980
(  0) 0) |
| [9] |
李庆芬. 断裂力学及其工程应用[M]. 哈尔滨: 哈尔滨工程大学出版社, 1998 (Li Qingfen. Fracture Mechanics and Engineering Application[M]. Harbin: Harbin Engineering University Press, 1998)
(  0) 0) |
| [10] |
洪起超. 工程断裂力学基础[M]. 上海: 上海交通大学出版社, 1987 (Hong Qichao. Basic Fracture Mechanics in Engineering[M]. Shanghai: Shanghai Jiaotong University Press, 1987)
(  0) 0) |
2. Wuhan Institute of Earthquake Engineering Co Ltd, 40 Hongshance Road, Wuhan 430071, China
 2018, Vol. 38
2018, Vol. 38

