2. 地壳运动与地球观测实验室,武汉市洪山侧路40号,430071;
3. 安徽省地震局,合肥市长江西路558号,230031;
4. 江西省地震局,南昌市洪都北大道865号,330039
重力异常场是实际地球的形状、质量分布与理论参考椭球体的差异,是地下物质分布不均匀在空间上的宏观表现,其作为地球的一种基本位场信息,是大地测量、地球物理、地质和海洋等学科的重要研究内容[1]。
重力异常场主要包括自由空气异常、布格重力异常和均衡重力异常,其计算的关键步骤是从自由空气异常中分别消除地形和假想“山根”的重力响应。早期布格异常计算通常忽略地形的影响,直到Hayford等[2]首次计算了地形起伏对重力的影响后,通常将未考虑地形起伏的布格异常称为简单重力布格异常,考虑地形起伏的布格异常称为完全重力布格异常,简称布格重力异常。目前,布格和均衡重力异常计算通常是分区域、分步、人工完成,还未见有自动化计算程序。这主要是由于地形改正和均衡改正需采用数字地形模型进行重力正演计算获得,涉及调用大量地形模型数据,且计算量较大。为简化其计算量,发展了多种计算算法,如Bullard等[3]提出布格改正由3个部分组成,即沿用至今的Bullard A、B、C体系;Hammer[4]采用块体同心环网格积分计算地形改正,给出地形改正查询表;Parker[5]采用平均地形模型,基于傅里叶变换快速计算地形改正;Cogbill[6]提出改进的曲率计算算法, 采用Kane[7]和Nagy[8]的近、远区地形改正公式和精密数字地形模型, 发布了高精度地形改正程序TCPackage,根据不同计算精度需求和计算能力,再采用不同的算法。近年来,即使是高度集成的重力数据处理软件,考虑到普通计算机运算速度和内存的限制,也只能将地形改正作为一个独立的计算模块,如美国Geosoft公司开发的地球科学成图和数据处理的软件Oasis montaj(http://www.geosoft.com/)和中国地质调查局编制的RGIS(http://www.drc.cgs.gov.cn/tech/201603/t20160309_266571.html)等。
随着现代大地测量技术的发展,多种局部地区或全球的数字地形模型公开发布,地形数据也存在多种数据格式、精度、覆盖范围,需借助其他地理信息软件提取、转换、拼接,使得重力异常计算的数据准备工作量较大,极大地限制了地形改正及均衡改正的计算速度。本文拟在计算服务器上建立数字地形数据库,设计地形提取、拼接算法,自动获取计算点邻近区域内的地形数据,通过云服务器强大的计算能力,快速、精确、自动计算得到相应区域或点位的重力异常场,可极大地降低重力异常场的计算成本。
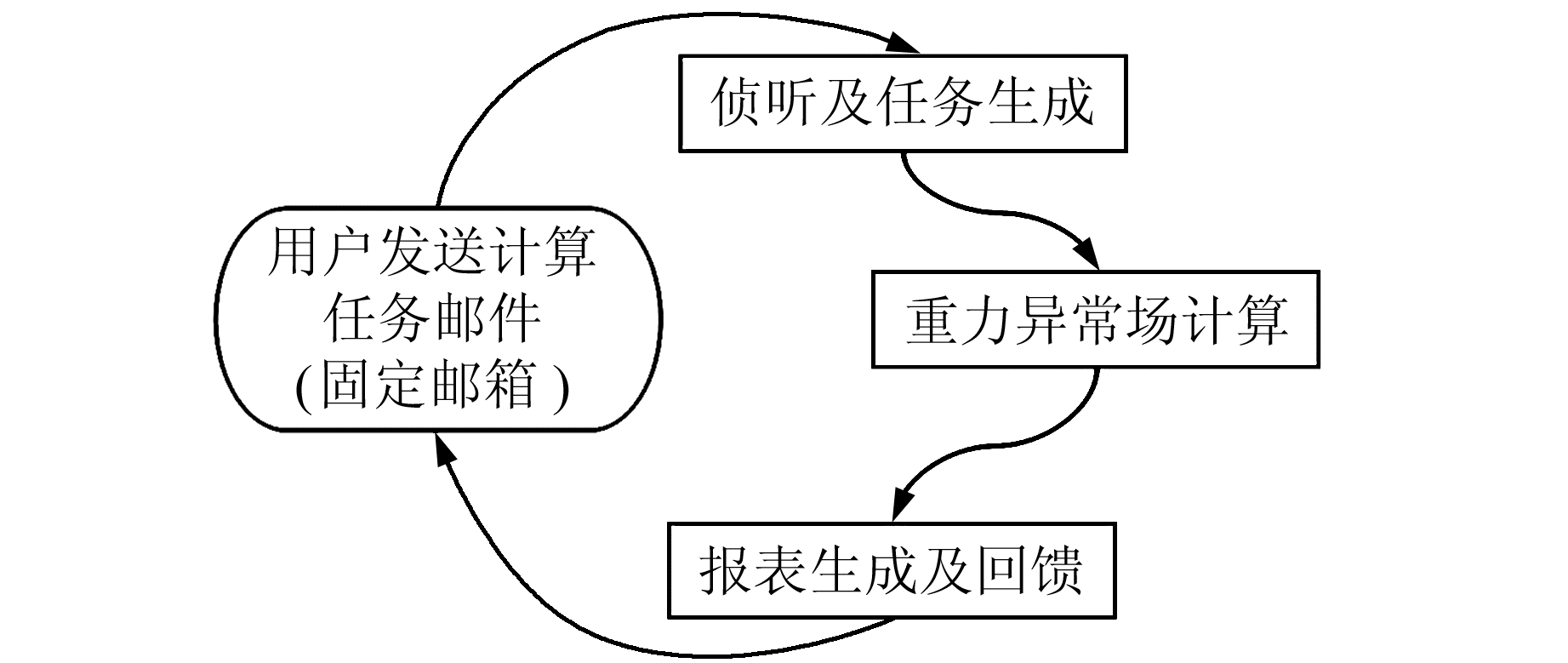
1 总体设计本软件主要分为3个功能模块,分别为侦听及任务生成、重力异常场计算、报表生成及回馈(图 1)。用户向指定邮箱发送计算任务邮件,侦听及任务生成模块定时扫描固定邮箱,如有新邮件则生成计算任务,同时调用重力异常场计算模块开始计算,重力异常场计算模块完成计算后,调用报表生成及回馈模块给当前用户发送报表及结果文件。为便于数据保密,计算系统处理的输入数据为计算点三维坐标(经度、纬度、高程坐标)和重力异常的假定值(结果返回后再自行替换为真实值)。
|
图 1 重力异常场云计算系统组成 Fig. 1 Cloud computing system framework of gravity anomaly field system |
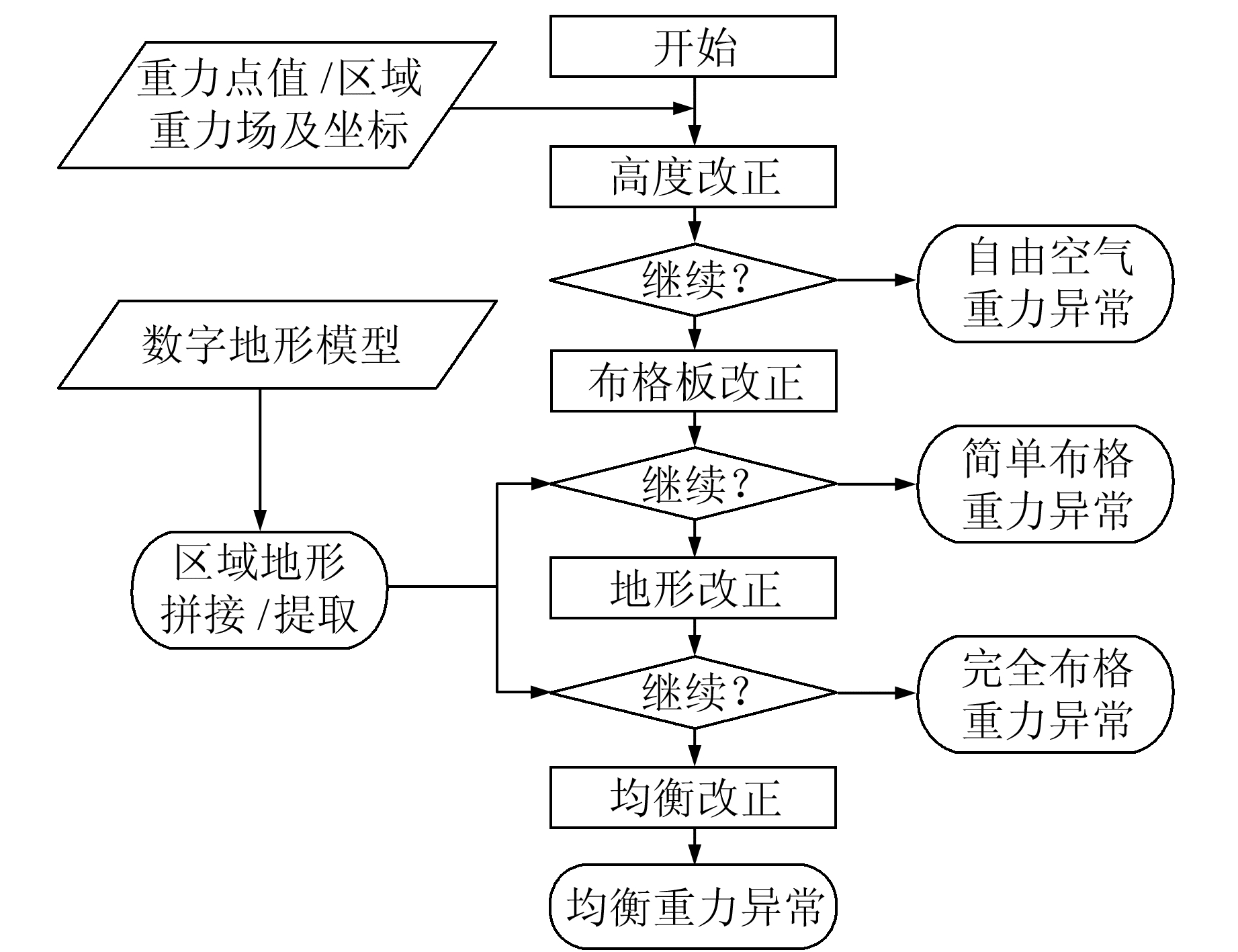
重力异常场计算模块主要完成异常场计算工作,既可以处理实际观测重力点位的重力异常值,也可以基于卫星测高和卫星重力场模型计算特定区域的重力异常场。本文中实际观测重力点位值是指经格值转换、仪器漂移、潮汐、仪器高、大气、极移改正及重力网(段)平差后得到的测点重力值。实测重力异常须依次经过经高度改正得到自由空气异常,经布格板改正(或称中间层改正)得到简单布格重力异常,经地形改正得到完全布格重力异常,再经均衡改正得到均衡重力异常,其计算流程见图 2。
|
图 2 重力异常场计算流程 Fig. 2 Calculation flow chart of gravity anomaly field |
回馈模块的主要功能是将计算结果通过邮件发送给当前任务的发件人,内容主要包括计算结果统计信息、采用的主要参数、参考基准、主要计算算法和计算结果文件等。
2 数据与主要算法 2.1 数据数字地形数据集主要有ASTER GDEM地形数据[9]、ETOPO(全球陆地海洋DEM高程数据)及其改进版TerrainBase[10]、SRTM数据(包括SRTM、SRTM15_PLUS、SRTM30_PLUS)[11]、全球30″陆地地形(GTOPO30)[12]、大洋地势图(GEBCO)[13]等。其中ASTER数据(-83°~83°N)空间分辨率达到1″×1″(约30 m); ETOPO数据分为1′、2′、5′三种网格精度; SRTM数据有1″和3″两种精度。此外,还有利用多种数据合成的全球地形模型,如SIO数据(scripps institute of oceanography)[14]利用海底地形数据和SRTM陆地数据合成全球地形数据,其中全球地形数据最新版本为V18.1。各数据具体精度见表 1。
|
|
表 1 常见陆地/海洋地形数据 Tab. 1 Common land/sea topographic data |
如计算区域重力异常场,则可提取卫星重力场模型,计算布格重力异常和均衡重力异常。目前,主要的卫星重力场模型有全球重力场模型EGM96[15]和EGM2008[16]。利用EGM2008重力场模型的球谐函数展开引力位系数可获得自由空气异常Δgf:
| $ \begin{align} & \Delta {{g}_{f}}=\frac{fM}{{{R}^{2}}}\sum\limits_{n=2}^{N}{\left( n-1 \right)\sum\limits_{m=0}^{n}{\left( {{\overline{C}}_{mn}}\cos m\lambda + \right.}} \\ & \left. \ \ \ \ \ \ \ \ \ \ {{\overline{S}}_{nm}}\sin m\lambda \right){{\overline{P}}_{mn}}\left( \cos \theta \right) \\ \end{align} $ | (1) |
式中,fM为地球引力常数,Cnm、Snm为完全正常化地球扰动引力位系数,θ为地心余纬,R为地球平均半径,λ为地心经度,Pnm(cosθ)为完全正常化缔合勒让德函数。
此外,SIO数据利用EGM2008数据和海洋船测重力合成全球重力场模型,其中全球重力场数据最新版本为V24.1。
2.2 主要算法本软件的正常场改正、高度改正、中间层改正、地形改正等计算公式参见文献[17]。地形改正中需要裁剪提取计算点周围地形计算其重力响应,通常将计算点周围区域按照近区Ri(0~30 m)、中区Rm(30 m~2 km)、远区Rd(20 km~166.735 km)划分为3个区域,因此需要提取计算点周围166.735 km的地形数据。166.735 km对应地球椭球经度长度为
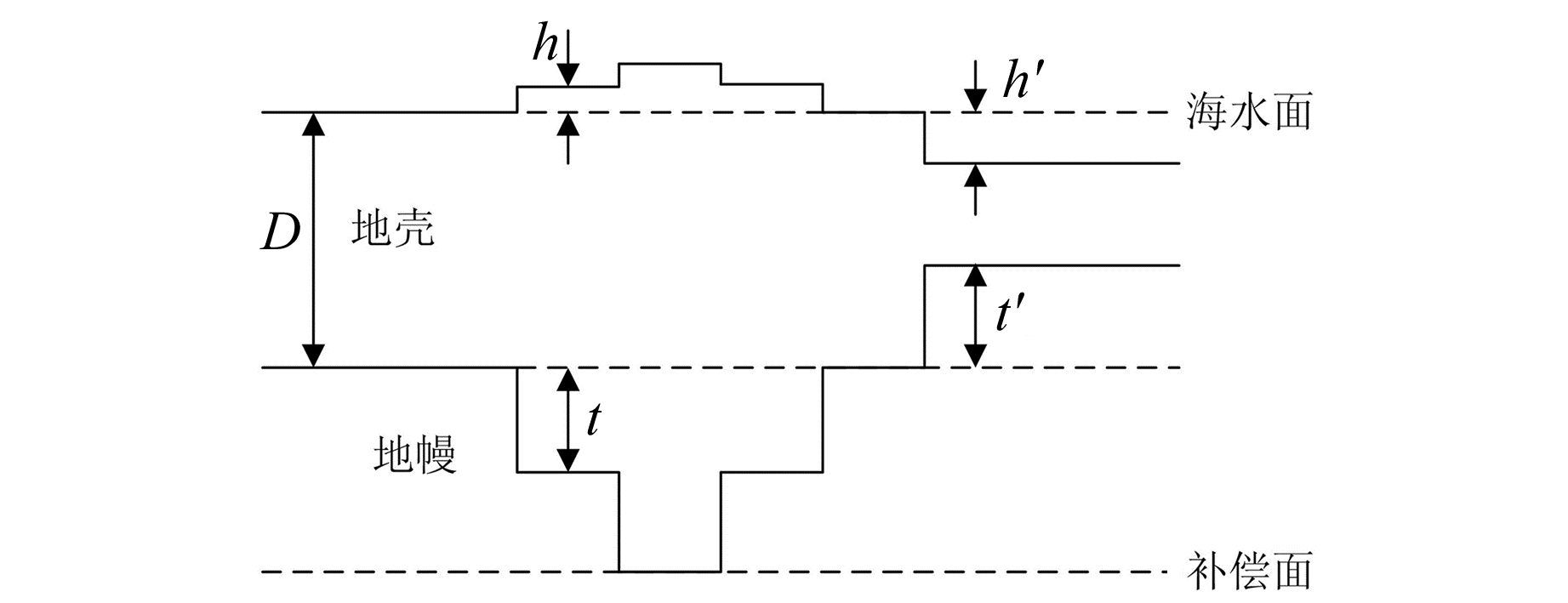
地壳均衡异常计算模型主要有艾黎-海斯卡宁均衡模型(简称艾黎模型)、普拉特-海福特均衡模型(简称普拉特模型)、维宁·迈尼兹模型、实验均衡模型和动态均衡模型,本文暂只考虑艾黎模型。均衡异常是在布格异常基础上进行均衡改正得到的,其实质是将实测重力值减去理论地球模型所产生的重力值,再把大地水准面外的质量移到地球内部以弥补质量亏损,最后将重力观测值归化到大地水准面上。艾黎模型见图 3。
|
图 3 艾黎模型 Fig. 3 Airy-Hesikanen isostatic compensation model |
图 3中,h为陆地地形高度,h′为海水深度,D为标准地壳厚度(30 km),t和t′分别为陆地和海洋补偿深度,海水平均密度ρw一般取1.027 g/cm3,地壳平均密度ρc一般取2.67 g/cm3,地幔平均密度ρm一般取3.27 g/cm3,则补偿密度为:
| $ \Delta \rho ={{\rho }_{m}}-{{\rho }_{c}}=0.6\ \text{g}/\text{c}{{\text{m}}^{3}} $ | (2) |
依据艾黎模型,陆地上的均衡补偿深度为:
| $ t=\frac{{{\rho }_{c}}}{\Delta \rho }h=4.45h $ | (3) |
海洋上的均衡补偿深度为:
| $ {t}'=\frac{{{\rho }_{c}}-{{\rho }_{w}}}{{{\rho }_{m}}-{{\rho }_{c}}}{h}'=2.73{h}' $ | (4) |
对重力场进行均衡改正,就是求出各个柱体的抵偿密度为Δρ的柱体对计算点的引力,从均衡模型可得,陆地均衡地壳厚度为:
| $ C=D+h+t $ | (5) |
海洋均衡地壳厚度为:
| $ {C}'={D}'-{h}'\text{-}{t}' $ | (6) |
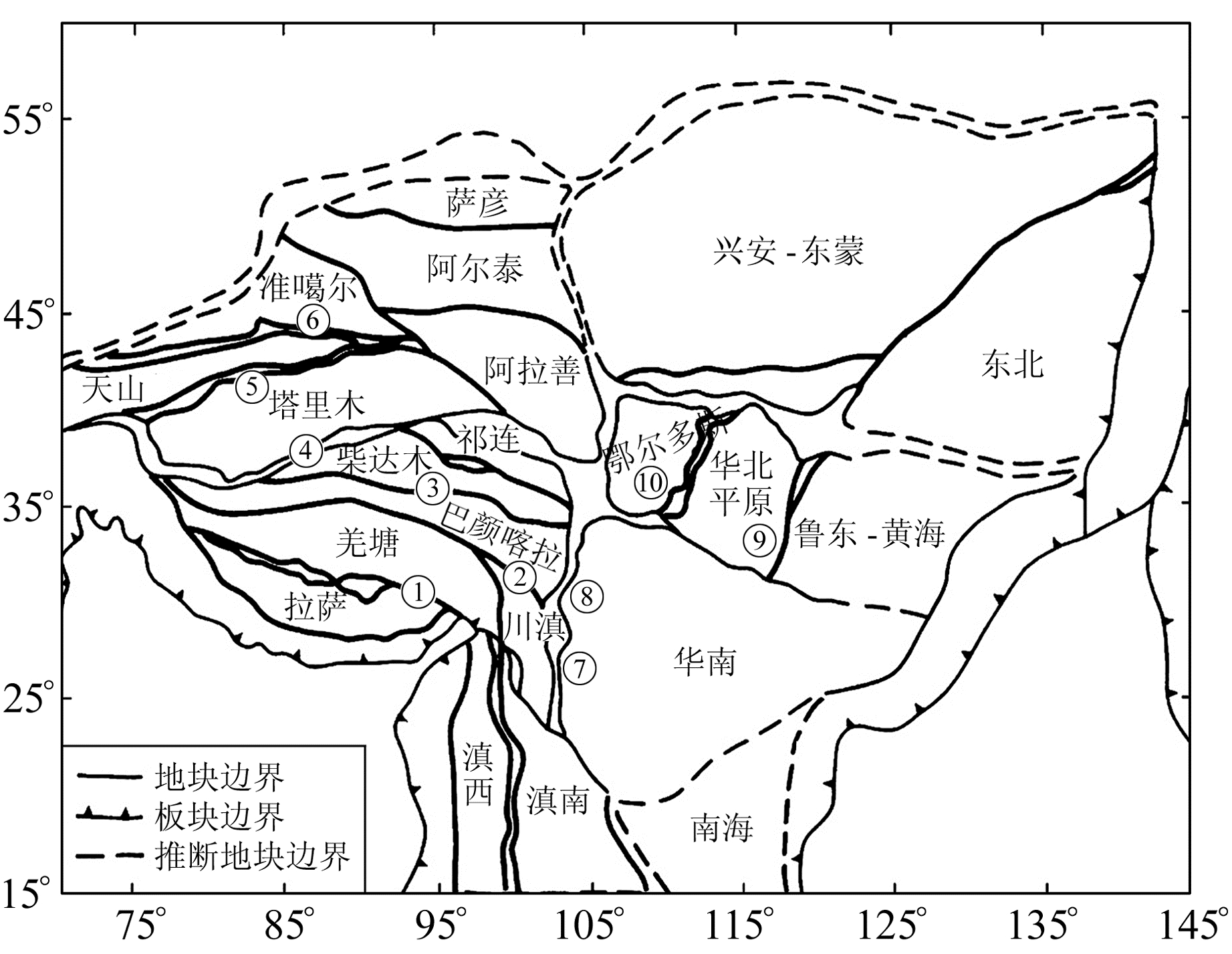
青藏高原东构造结及邻区(88°~106°E,20°~35°N)位于阿尔卑斯-印支特提斯构造带东段与太平洋构造带的交汇部位, 是由劳亚与冈瓦纳大陆之间诸多地体或陆块构成的复杂造山带[18]。该区主要包括印度板块和拉萨地块、羌塘地块、巴颜喀拉地块、扬子地块前缘(四川盆地)、川滇地块、滇西地块、滇缅地块等二级块体。这些块体在印度板块的推挤作用下,物质向青藏高原东部及南部迁移,围绕青藏高原东构造结产生顺时针旋转(图 4)。研究表明,该区域内地震均与此构造运动密切相关。
布格异常反映地壳内部密度分布的不均匀特征,均衡重力异常反映地壳垂向构造应力分布特征,通过重力异常场的分析,可加深对该区域动力构造环境的认识。该地区有一半以上的面积尚没有重力测点, 是重力数据空白区[19], 本文采用SIO数据计算其布格重力异常和均衡重力异常,以此来测试重力异常场云计算软件系统性能。
3.1 青藏高原东构造结及邻区重力异常场计算采用SIO数据,其中全球地形数据版本为V18.1(图 4),全球卫星重力场数据版本为V24.1(图 5),按5′×5′数据分辨率。该区地形高差起伏较大,高差范围约为-1 000~7 000 m,涵盖了喜马拉雅山和部分印度洋区域,其在印度板块与拉萨地块、川滇地块与四川盆地均显示急剧变化的地形特征。自由空气异常变化范围约为-300~600 mGal(图 6), 变化特征与地形基本一致,表明其与地形变化密切相关。

|
图 5 青藏高原东缘数字地形模型 Fig. 5 Terrain model of the eastern Tibetan plateau |
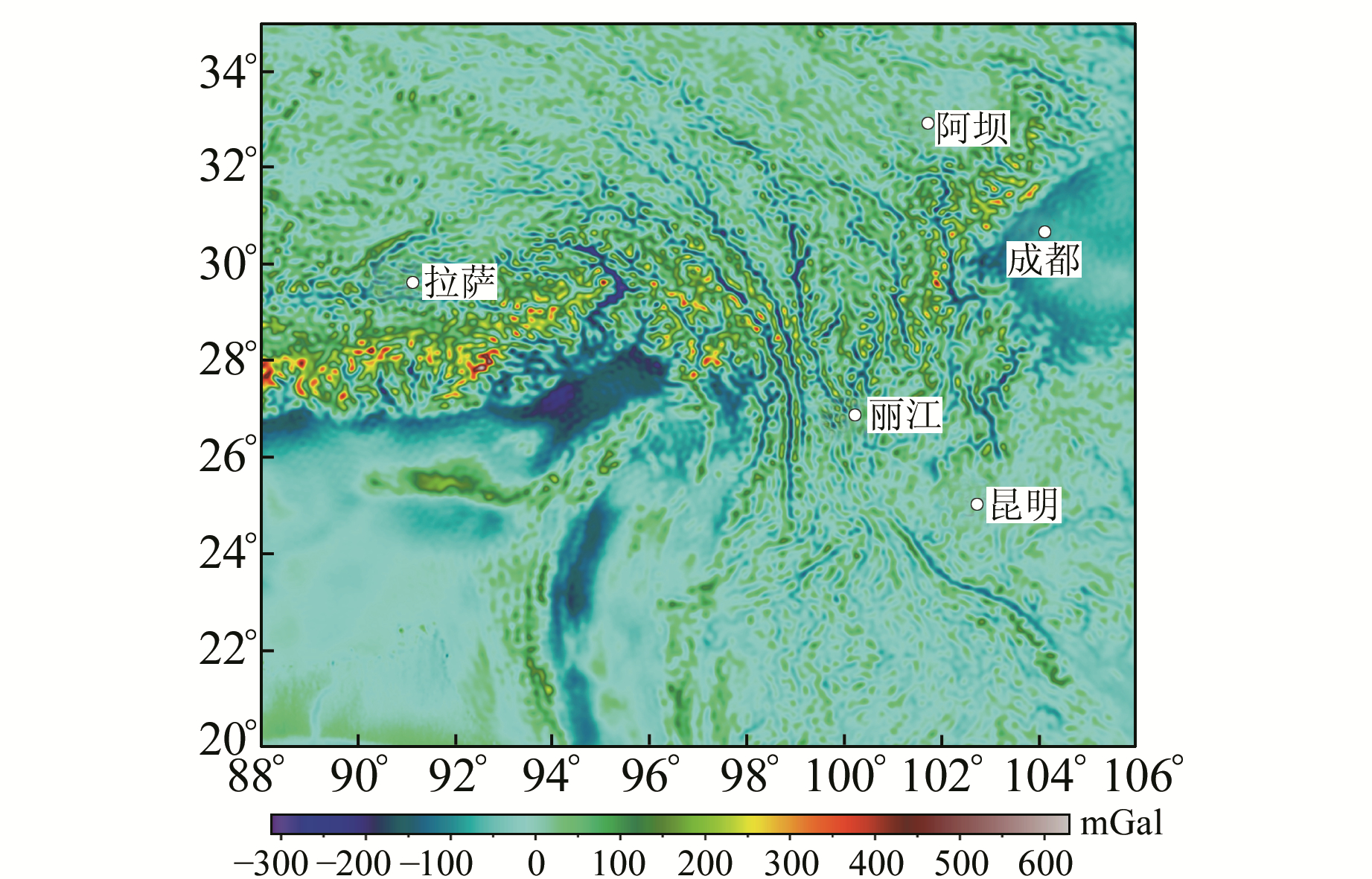
|
图 6 青藏高原东缘自由空气异常 Fig. 6 Free air anomalies of the eastern Tibetan plateau |
利用重力异常场计算软件系统,对青藏高原东构造结及邻区布格重力异常和均衡重力异常进行计算,得到该区域布格重力(图 7)和均衡重力异常(图 8)。布格重力异常变化范围约为-500~0 mGal, 以青藏高原东缘及南缘为异常陡变带,以其为界,青藏高原内部布格异常均低于-300 mGal, 青藏高原及东构造结以东区域负异常逐渐减小。印度大陆大部分区域在零值附近,地壳结构表现为稳定的地台特征。

|
图 7 青藏高原东缘布格重力异常 Fig. 7 Bouguer anomalies of the eastern Tibetan plateau |
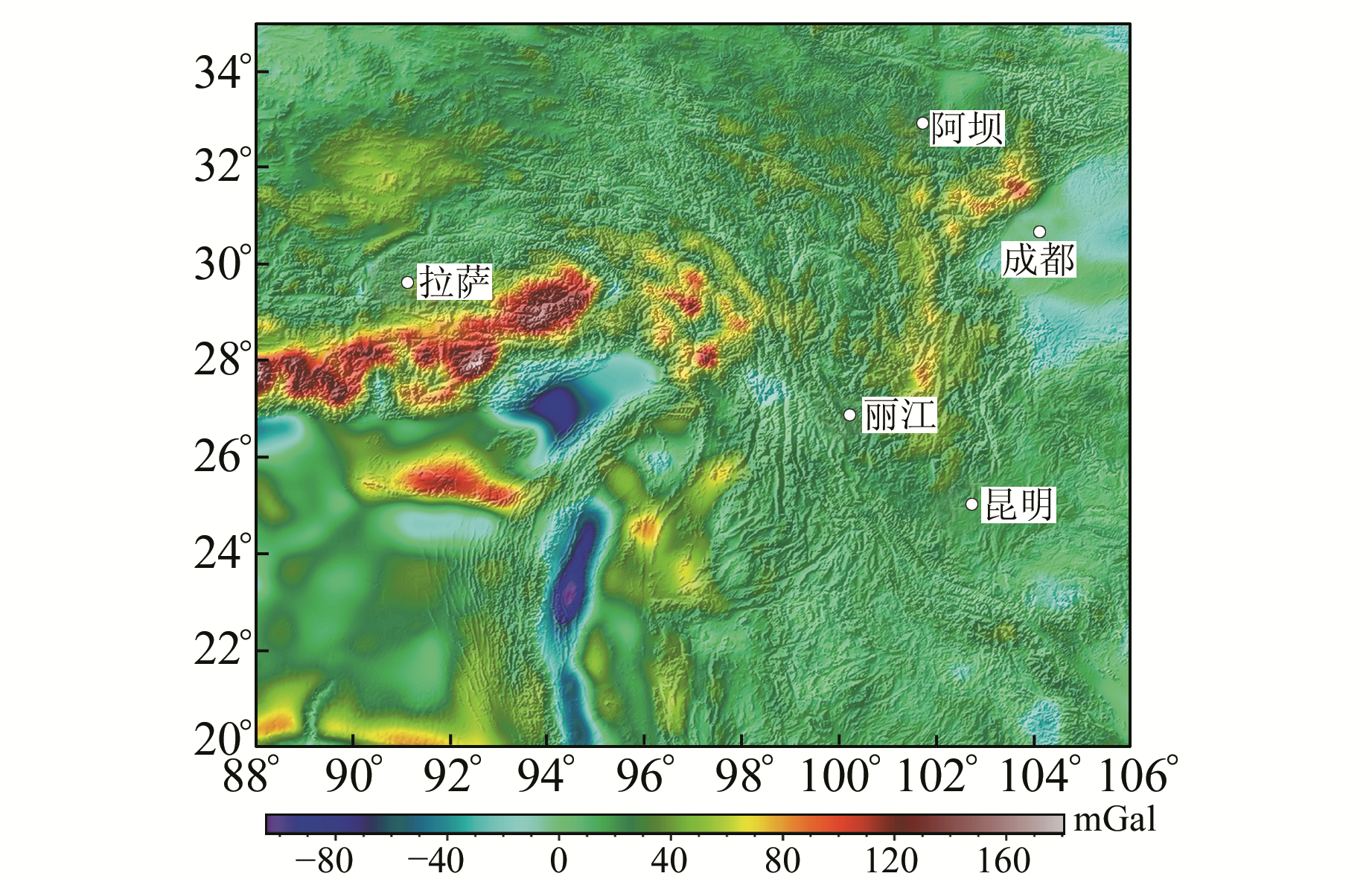
|
图 8 青藏高原东缘均衡重力异常 Fig. 8 Isostatic gravity anomalies of the eastern Tibetan plateau |
上述布格重力异常计算结果与滕吉文等[20]的结果显示基本一致的特征,其极值略有差异,可能与所采用的重力场模型及地形数据不同有关。均衡异常计算中对“山根”重力效应的计算与布格异常计算所采用的地形改正算法一致,可见本文云计算程序结果是可靠的。
3.2 计算性能分析对于青藏高原东构造结及邻区重力异常场,共计算22 032个点位,计算区域范围为18°×15°。为减少不必要的内存消耗,设置程序自动按照4°×4°区块切割,共分为20个计算区块。地形和重力数据统一转换为广泛应用于大气科学、水文、海洋学、环境模拟、地球物理等诸多领域的NetCDF格式(http://www.unidata.ucar.edu/software/netcdf/),该数据格式便于存储和交换。程序可自动按照设置好的地形数据库路径分别为每个区块准备6°×6°范围的地形数据(外延2°),无需如Geosoft、RGIS等单独进行人工转换、切割、拼接各计算区域的地形数据,可节省大量人工成本。
利用4核48线程、主频2.6 GHz的英特尔至强处理器E5-4607的测试服务器进行计算,程序采用并行计算,自动开启48个并行线程,耗时约6 h。该计算在1核8线程、主频2.7 GHz英特尔Core i7-3740QM处理器的移动工作站上运行约4 d可完成,计算效率是移动工作站的16倍。通过云服务器提供共享计算,其计算算法可根据最新研究成果即时予以改进,硬件计算性能也能不断更新,普通用户不必为计算重力异常场购置专用服务器。因此,重力异常场云计算软件系统不仅可提高计算速度,也可节约计算成本和人工成本。
4 结语本文开发的跨平台重力异常场云计算软件系统OnGra解决了目前重力异常场计算繁琐、速度慢、无法自动处理等问题,极大改善了标准化计算和快速输出结果,并得到验证。该云计算软件系统具有以下特点:
1) 统一了不同数据格式、处理流程、参数选取等,可根据最新研究成果,实时更新计算算法,自适应提取计算区域数字地形模型并输出结果。
2) 借助高性能工作站实现了重力异常场计算的标准化、快速(并行)化、智能化,提高了重力观测数据的处理效率。
| [1] |
杨金玉, 张训华, 张菲菲, 等. 应用多种来源重力异常编制中国海陆及邻区空间重力异常图及重力场解读[J]. 地球物理学报, 2014, 57(12): 3920-3931 (Yang Jinyu, Zhang Xunhua, Zhang Feifei, et al. Preparation of the Free-Air Gravity Anomaly Map in the Land and Seas of China and Adjacent Areas Using Multi-Source Gravity Data and Interpretation of the Gravity Field[J]. Chinese J Geophys, 2014, 57(12): 3920-3931 DOI:10.6038/cjg20141206)
(  0) 0) |
| [2] |
Hayford J F, Bowie W. Geodesy:The Effect of Topography and Isostatic Compensation upon the Intensity of Gravity[M]. Washington: US Gove Print Off, 1912
(  0) 0) |
| [3] |
Bullard E C. Gravity Measurements in East Africa[J]. Philosophical Transactions of the Royal Society, 1936, 235(757): 445-534 DOI:10.1098/rsta.1936.0008
(  0) 0) |
| [4] |
Hammer S. Terrain Corrections for Gravimeter Stations[J]. Geophysics, 1939, 4(3): 184-194 DOI:10.1190/1.1440495
(  0) 0) |
| [5] |
Parker R L. The Rapid Calculation of Potential Anomalies[J]. Geophysical Journal International, 1973, 31(4): 447-455 DOI:10.1111/j.1365-246X.1973.tb06513.x
(  0) 0) |
| [6] |
Cogbill A. Gravity Terrain Corrections Calculated Using Digital Elevation Models[J]. Geophysics, 1990, 55(1): 102-106 DOI:10.1190/1.1442762
(  0) 0) |
| [7] |
Kane M F. A Comprehensive System of Terrain Corrections Using a Digital Computer[J]. Geophysics, 1962, 27(4): 455-462 DOI:10.1190/1.1439044
(  0) 0) |
| [8] |
Nagy D. The Geravitational Attraction of a Right Rectangular Prism[J]. Geophysics, 1966, 30(4): 362-371
(  0) 0) |
| [9] |
ASTER GDEM Validation Team. ASTER Global Dem Validation Summary Report[R]. METI/ERSDAC NASA/LPDAACUSGS/EROS, 2009 https://www.mendeley.com/research-papers/aster-global-dem-validation/
(  0) 0) |
| [10] |
Amante C, Eakins B W. ETOPO1 Arc-Minute Global Relief Model: Proce-Dures, Data Sources and Analysis[EB/OL]. http://www.ngdc.noaa.gov/mgg/global/global.html, 2009
(  0) 0) |
| [11] |
Bamler R. The SRTM Mission: A World-Wide 30 m Resolution DEM from SAR Interferometry in 11 Days[C]. Photogrammetric Week '99', Wichmann Verlag, Heidelberg, 1999 https://www.researchgate.net/publication/224000358_The_SRTM_mission_A_world-wide_30_m_resolution_DEM_from_SAR_interferometry_in_11_days
(  0) 0) |
| [12] |
LP DAAC. Global 30 Arc-Second Elevation Data Set GTOPO30[EB/OL]. http://decdaac.usgs.gov/gtopo30.asp, 2004
(  0) 0) |
| [13] |
Becker J J, Sandwell D T, Smith W H, et al. Global Bathymetry and Elevation Data at 30 Arc Seconds Resolution: SRTM30_PLUS[J]. Marine Geodesy, 2009, 32(4): 355-371 DOI:10.1080/01490410903297766
(  0) 0) |
| [14] |
Sandwell D T, Smith W H. Global Marine Gravity from Retracked Geosat and ERS-1 Altimetry: Ridge Segmentation versus Spreading Rate[J]. J Geophys Res, 2009, 114(B1)
(  0) 0) |
| [15] |
Smith D A. There Is No Such Thing as "THE"EGM96 Geoid: Subtle Points on the Use of a Global Geopotential Model[C]. IGES Bulletin No. 8, International Geoid Service, Milan, 1998 http://www.researchgate.net/publication/285027356_There_is_no_such_thing_as_The_EGM96_geoid_Subtle_points_on_the_use_of_a_global_geopotential_model
(  0) 0) |
| [16] |
Pavlis N K, Holmes S A, Kenyon S C, et al. The Development and Evaluation of the Earth Gravitational Model 2008 EGM2008)[J]. Journal of Geophysics Research: Solid Earth, 2012, 117(B4)
(  0) 0) |
| [17] |
杨光亮, 申重阳, 孙少安, 等. 类乌齐-玉树-玛多剖面重力异常研究[J]. 大地测量与地球动力学, 2011, 31(5): 1-4 (Yang Guangliang, Shen Chongyang, Sun Shao'an, et al. Study on Gravity Anomaly of Profile Riwoqe-Yushu-Maduo[J]. Journal of Geodesy and Geodynamics, 2011, 31(5): 1-4)
(  0) 0) |
| [18] |
Royden L H, Burchfiel B C, King R W, et al. Surface Deformation and Lower Crustal Flow in Eastern Tibet[J]. Science, 1997, 276(5313): 788-790 DOI:10.1126/science.276.5313.788
(  0) 0) |
| [19] |
张培震, 邓起东, 张国民, 等. 中国大陆的强震活动与活动地块[J]. 中国科学:地球科学, 2003, 33(B4): 12-20 (Zhang Peizhen, Deng Qidong, Zhang Guomin, et al. Strong Earthquake Activity and Active Block in the Mainland of China[J]. Science China Earth Science, 2003, 33(B4): 12-20)
(  0) 0) |
| [20] |
滕吉文, 王谦身, 王光杰, 等. 喜马拉雅东构造结地区的特异重力场与深部地壳结构[J]. 地球物理学报, 2006, 49(4): 1045-1052 (Teng Jiwen, Wang Qianshen, Wang Guangjie, et al. Specific Gravity Field and Deep Crustal Structure of the 'Himalayas East Structural Knot'[J]. Chinese J Geophys, 2006, 49(4): 1045-1052)
(  0) 0) |
2. Crustal Movement Laboratory, 40 Hongshance Road, Wuhan 430071, China;
3. Anhui Earthquake Agency, 558 West-Changjiang Road, Hefei 230031, China;
4. Jiangxi Earthquake Agency, 865 North-Hongdu Road, Nanchang 330039 China
 2018, Vol. 38
2018, Vol. 38