2. 中国地震局地壳应力研究所武汉科技创新基地,武汉市洪山侧路40号,430071
伺服控制系统是绝对重力仪研制的关键环节之一[1-2]。目前,绝大部分重力仪采用机械传动来实现落体的伺服控制,如基于齿轮齿条传动的A10[3]、基于钢带式传动的FG-5[4]、FG-5X[5]等。用凸轮驱动器代替落体的伺服控制系统[6-7],可使绝对重力仪结构小巧、测量效率高、便于携带,是绝对重力仪发展的重要方向之一。2005年Faller等研制的凸轮式绝对重力仪参加第七次国际重力仪比对,但无凸轮驱动器设计方面的报道。吴书清等[8]搭建了凸轮式绝对重力仪测量系统,也未涉及凸轮驱动器的设计。余斌彬等[9]采用四次多项式函数设计凸轮轮廓曲线,但未实现无柔性冲击的特征,且加速度较大,易导致构件之间磨损,运动精度下降。
本文提出一种自由落体凸轮驱动器结构设计方法,采用凸轮机构代替伺服控制系统,利用等加速等减速运动规律获得绝对重力仪需要的自由落体运动控制,并通过SolidWorks进行建模与运动仿真。
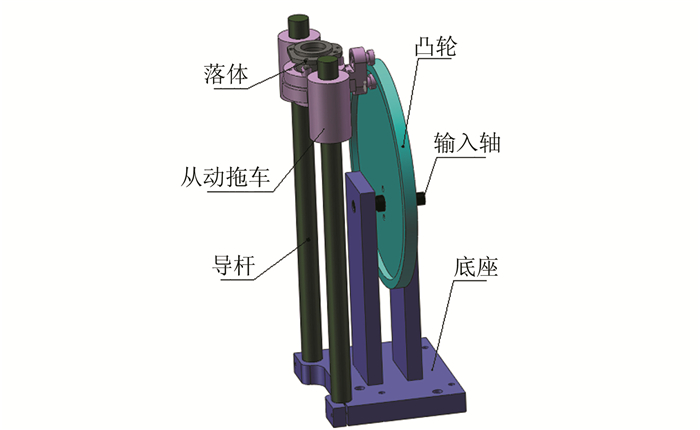
1 构成与工作原理自由落体凸轮驱动器总体结构如图 1所示,其工作原理[10]是:输入轴匀速转动带动凸轮转动,凸轮带动从动支架上下往复运动,质量不超过200 g的落体静止放置在从动支架上。当凸轮由远程端开始转动时,凸轮带动从动支架以略大于重力加速度的加速度加速,从动支架释放搁置在其上的落体并与落体的间距逐渐增大。当落体与从动支架的间距增大到设计值时,保持恒定距离不变,直到落体自由下落过程结束。在落体下落结束时,从动支架减速并平稳接住落体,此过程无刚性冲击,从而实现落体的软承接。最后从动支架再向上把落体举到初始位置,由此周而复始地实现自由落体的释放、自由下落、软承接和提升4个阶段。通过拟合大量的落体在自由下落阶段的距离和时间值,即可得到绝对重力值。
|
图 1 总体结构 Fig. 1 General structure |
为避免凸轮驱动器零件之间的尺寸干涉,设计落体最低位置距离输入轴轴心65.6 mm,将落体的释放、自由下落、软承接3个阶段行程分别设计为1.36 mm、22.4 mm、30.64 mm,因此落体最高点距离输入轴轴心120 mm。要求落体在释放初始阶段即与从动支架脱开,并在释放阶段末端落体与从动支架脱开距离达到2 mm;在自由下落阶段从动支架与落体始终保持恒定距离p=2 mm;软承接阶段从动支架逐渐减少与落体的间距,直到平稳接住落体并减速到零;提升阶段从动支架推动落体提升,并在提升阶段末端的速度值为零。要保证凸轮驱动器满足自由落体运动的要求,必须选用合适的从动件运动规律。最大加速度是影响机构运动特性的重要参数,等加速等减速运动规律具有最小的最大加速度值,是一种最适合中速轻载的运动规律[10],因此采用该规律来模拟自由落体运动。
2.1 数学模型设S、V、A分别为从动拖车在某一段上的位移、速度、加速度,其表达式为:
| $ S = {C_0} + {C_1}t + {C_2}{t^2} $ | (1) |
| $ V = {C_1} + 2{C_2}t $ | (2) |
| $ A = 2{C_2} $ | (3) |
式中,Ci(i=0, 1, 2)为待求系数,t为从动拖车时间。
2.2 求解设输入轴转速n=200 rpm,时间因子a=
1) 释放阶段(0≤t<2 a)采用等加速等减速运动规律。该阶段从动支架与落体逐渐脱离,当t=0.02 s时从动拖车与落体分开距离p=2 mm。边界条件及连续性条件为:起始位置位移为120 mm,速度为零;末端位置的位移比落体低2 mm;中间位置的位移比落体低1 mm。
2) 自由下落阶段(2a≤t<8a)采用二项式运动规律。该阶段位移始终比落体低2 mm。
3) 软承接阶段(8a≤t<16a)采用等加速等减速运动规律。该阶段从动支架逐渐减少与落体的间距,直到平稳接住落体并减速到零。分为抓取和减速调整两个过程:抓取过程(8a≤t<10 a)的边界条件及连续性条件为起始位置位移和速度连续,末端位置的位移和速度与落体一致,刚好接住落体,中间位置的位移比落体低1 mm;减速调整过程(10 a≤t<16 a)的边界条件及连续性条件为从动拖车拖住落体减速到零,起始位置位移和速度连续,末端位置速度为零。
4) 提升阶段(16 a≤t<36 a)采用等加速等减速运动规律。从动支架推动落体提升,并保证在远程端的速度为零。该阶段边界条件及连续性条件为起始位置位移和速度连续,末端位置的速度为零,位移为120 mm,中间位置从动拖车上升位移量为总行程量的一半。
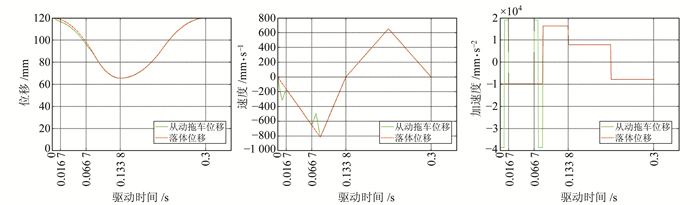
2.3 运动曲线将设定的边界条件及连续性条件代入式(1)~(3),计算各段曲线对应的系数Ci(i=0, 1, 2),求凸轮驱动器运动方程,如表 1所示,落体与从动拖车的运动学规律如图 2所示。
|
图 2 落体与从动拖车的运动学规律 Fig. 2 Kinematical event of free-falling body and follower |
|
|
表 1 凸轮驱动器与落体运动方程 Tab. 1 Motion equation of cam driver and free-falling body |
由表 1和图 2看出,速度曲线连续,且无刚性冲击;加速度在各阶段中间位置发生突变,会产生柔性冲击,但落体载荷较轻,可用于中速低载场合。凸轮的轮廓曲线具有一定的合理性,满足绝对重力仪自由落体运动的要求。
3 凸轮驱动器的设计与运动仿真 3.1 设计为保证凸轮从动件和轮廓始终接触,根据机构的封闭方式可分为力封闭型和几何封闭型两种。共轭凸轮属于后者,具有接触应力小、传动精度高等特点,具有良好的转动特性和动力学特性,适用于中高速场合[11]。自由落体凸轮驱动器是利用同侧双滚子形锁合共轭盘形凸轮实现的,从动支架有两个滚子(图 1),其中一个借助外力牵制另外一个运动,使凸轮能与从动支架始终保持接触,从而在振动、噪音、磨损等方面得到有效控制。设滚子直径φ=12 mm,双滚子中心距d=19.8 mm。由表 1获得凸轮理论廓线的位移时间数据点导入到SolidWorks的线性马达驱动从动支架,设置运动周期0.3 s,给驱动凸轮的输入轴添加角速度为200 rpm的旋转马达,跟踪双滚子圆心的运动轨迹,再利用这两条运动轨迹曲线求得等距6 mm的凸轮实际廓线,分别拉伸、切除即可得到三维凸轮模型[12]。完成设计的凸轮模型如图 3所示,图中两条红色细实线为双滚子圆心的运动轨迹。将设计好的凸轮模型另存为IGS格式,即可供其他CAM软件进行调用。

|
图 3 凸轮模型 Fig. 3 Model of cam |
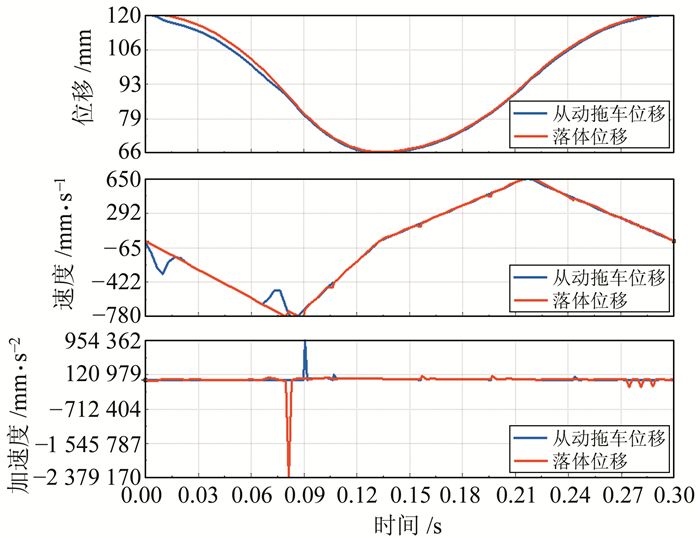
将设计好的凸轮模型装入装配体,设置凸轮与从动拖车的配合关系为“凸轮配合”。在motion中取消从动拖车的线性马达,添加重力方向,进行仿真计算,则从动拖车和落体在重力方向的位移、速度和加速度曲线如图 4所示。
|
图 4 落体与从动拖车的仿真运动学规律 Fig. 4 Simulation kinematical event of free-falling body and follower |
对比图 4与图 2的位移、速度曲线看出,自由落体凸轮驱动器的运动规律与设计要求基本相符。由图 4的加速度仿真曲线看出,落体在被从动拖车接住的瞬间冲击较大,加速度在运动规律变化的始末位置发生突变,产生柔性冲击,这都是引起凸轮驱动器振动噪音的主要来源。运动仿真是在未考虑传动系统间隙的理想情况下进行的,在实验样机的制造过程中,可以在间隙中填充相应的润滑介质以减小振动[13]。
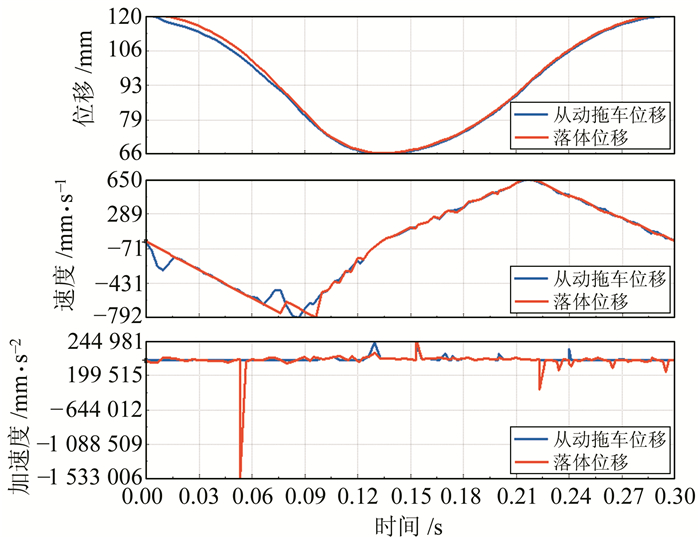
3.3 误差分析设凸轮加工误差的均值μ=0,均方根差σ=0.02 mm,将Matlab生成的正态分布函数代入凸轮廓线中,对凸轮驱动器进行运动仿真,其运动曲线如图 5所示。
|
图 5 落体与从动拖车的仿真运动学规律(代入凸轮径向误差) Fig. 5 Simulation kinematical event of free-falling body and follower(radial error of cam is substituted into the model) |
对比图 4与5看出,代入凸轮径向误差的凸轮驱动器的位置曲线无明显变化,但对运动特性产生影响,振动和冲击均明显加强。在实验样机的设计过程中,可通过机械结构惯性平衡优化的方法减小凸轮驱动器的振动和冲击。
利用凸轮驱动器实现落体的释放、自由下落、软承接和提升4个阶段,采用SolidWorks motion进行建模仿真,可为加工提供理论基础。
| [1] |
刘达伦, 吴书清, 徐进义, 等. 绝对重力仪研究的最新进展[J]. 地球物理学进展, 2004, 19(4): 739-742 (Liu Dalun, Wu Shuqing, Xu Jinyi, et al. The New Evolution of Absolute Gravimeter[J]. Progress in Geophysics, 2004, 19(4): 739-742)
(  0) 0) |
| [2] |
邢乐林, 申重阳, 李辉, 等. 欧洲Walferdange绝对重力仪比对观测[J]. 大地测量与地球动力学, 2009, 29(3): 77-79 (Xing Lelin, Shen Chongyang, Li Hui, et al. Comparative Observation of Absolute Gravimeters in Walferdange[J]. Journal of Geodesy and Geodynamics, 2009, 29(3): 77-79)
(  0) 0) |
| [3] |
王林松, 陈超, 王同庆, 等. A-10绝对重力仪野外测量精度分析[J]. 大地测量与地球动力学, 2012, 32(1): 60-64 (Wang Linsong, Chen Chao, Wang Tongqing, et al. Analysis of Measuring Accuracy in Field with A-10 Absolute Gravimeter[J]. Journal of Geodesy and Geodynamics, 2012, 32(1): 60-64)
(  0) 0) |
| [4] |
Niebauer T M, Sasagawa G S, Faller J E, et al. A New Generation of Absolute Gravimeters[J]. Metrologia, 2005, 32(3): 159-180
(  0) 0) |
| [5] |
李建国, 李辉, 张松堂, 等. 中国绝对重力仪第二次比对测量[J]. 大地测量与地球动力学, 2014, 34(4): 64-66 (Li Jianguo, Li Hui, Zhang Songtang, et al. Results of the Second Contrast Observation of Absolute Gravimeters(CCAG-2013)[J]. Journal of Geodesy and Geodynamics, 2014, 34(4): 64-66)
(  0) 0) |
| [6] |
Faller J E, Niebauer T M, Vitoucrine A L. Rotary Cam Driven Free Fall Dropping Chamber Mechanism: US6298722B1[R]. 2001
(  0) 0) |
| [7] |
Faller J E. The Measurement of Little g: A Fertile Ground for Precision Measurement Science[J]. Journal of Research of the National Institute of Standards & Technology, 2005, 110(6): 559-581
(  0) 0) |
| [8] |
吴书清, 刘达伦, 徐进义, 等. 凸轮式绝对重力仪的研制进展[C]. 中国地球物理学会第25届年会, 合肥, 2009 (Wu Shuqing, Liu Dalun, Xu Jinyi, et al. The Development of the Cam Absolute gravimeter[C]. The 25th Annual Meeting of Chinese Geophysics Society, Hefei, 2009)
(  0) 0) |
| [9] |
余斌彬, 黄曲红, 安治国, 等. 绝对重力仪的凸轮廓线设计[J]. 测绘地理信息, 2015, 40(1): 18-21 (Yu Binbin, Huang Quhong, An Zhiguo, et al. Cam Profile Design of Absolute Gravimeter[J]. Journal of Geomatics, 2015, 40(1): 18-21)
(  0) 0) |
| [10] |
刘昌祺, 牧野洋, 曹西京. 凸轮机构设计[M]. 北京: 机械工业出版社, 2005 (Liu Changqi, Mu Yeyang, Cao Xijing. Cam Mechanism Design[M]. Beijing: China Mechine Press, 2005)
(  0) 0) |
| [11] |
李艳莉, 张海燕, 李茂斌. 基于MATLAB和SolidWorks软件的共轭凸轮设计及运动仿真[J]. 轻工机械, 2008, 26(1): 52-54 (Li Yanli, Zhang Haiyan, Li Maobin. Design and Motion Simulation of Conjugating Cams Based on MATLAB and SolidWorks[J]. Light Industry Machinery, 2008, 26(1): 52-54)
(  0) 0) |
| [12] |
陈详超, 胡其登. SolidWorks Motion运动仿真教程[M]. 北京: 机械工业出版社, 2012 (Chen Xiangchao, Hu Qideng. SolidWorks Motion Simutation Tutorial[M]. Beijing: China Machine Press, 2012)
(  0) 0) |
| [13] |
相立峰. 基于ADAMS和SolidWorks的印刷机凸轮传动系统的性能分析与优化设计[D]. 南京: 南京信息工程大学, 2011 (Xiang Lifeng. Performance Analysis and Optimized Design of Cam Drive System of Rotary Press Based on ADAMS and SolidWorks[D]. Nanjing: Nanjing University of Information Science & Technology, 2011)
(  0) 0) |
2. Wuhan Base of Institute of Crustal Dynamics, CEA, 40 Hongshance Road, Wuhan 430071, China
 2018, Vol. 38
2018, Vol. 38


