2. 中国地震局地壳应力研究所,北京市安宁庄路1号,100085
水位是地震地下流体台网监测的主要测项,通过对地下水位观测资料的分析可获得多种地壳应力、应变信息, 如地球固体潮、气压变动、地震波扰动、地球自由震荡、地面水体负荷、液核动力学效应等[1]。我国地震地下水位动态观测仪器主要包括模拟观测仪器和数字观测仪器,其中数字水位仪比例为70%,包括LN-3(A)、SWY-1(Ⅱ)、ZKGD3000、DRSW-1等型号[2],均为压力式水位仪。数字压力式水位仪具有灵敏度高、动态响应快、测量精度高等特点。十多年的运行情况表明,绝大部分仪器运行良好,最大观测误差不大于0.2%FS,符合地震井水位观测要求,但也有一些仪器存在明显的零漂现象[3-4],观测误差较大。本文对压力式水位仪观测误差来源及其影响程度进行分析,并结合近年来多次水位仪招标仪器的测试情况,提出相应的测试方法。
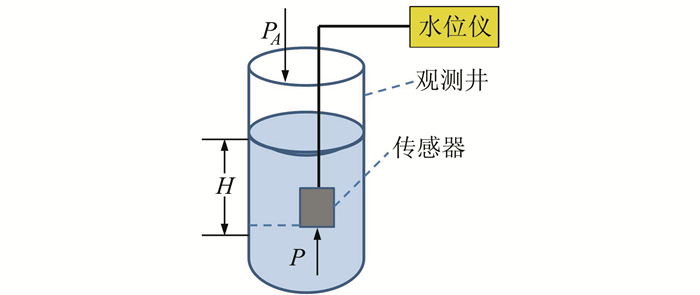
1 观测误差来源压力式水位仪工作原理是把压力传感器固定在水面以下某一深度,通过测量液体内部压强的方法来测量水位。如图 1所示,P为水位传感器测得的总压力值,PA为井口大气压力值,ρ为观测井水密度,g为观测井点重力加速度。压力式水位仪器测得的水位值H(传感器与水位的高度)可以表示为:
|
图 1 压力式水位仪测量原理 Fig. 1 Schematic diagram of measuring principle of pressure type water level meter |
| $ H(\rho, g, P, {P_A}) = (P-{P_A})/\left( {\rho g} \right) $ | (1) |
目前在地震系统使用的数字压力式水位仪包括差压式和绝压式两种类型。绝压式水位仪中(如ZKGD型水位仪),PA通过水位仪自带的气压仪测得;差压式水位仪(如LN-3系列、SWY系列)则是在水位传感器电缆线内增加一条导气管,通过导气管与大气连通对传感器进行气压补偿[5-6], 水位传感器测得的压力值即为水柱高度压力值P,式(1)简化为:
| $ H\left( {p, g, P} \right) = P/\left( {\rho g} \right) $ | (2) |
根据压力式水位仪的测量原理,水位仪的测量属于间接测量,其观测误差来源于总压力测量误差(Δp)、大气压测量误差(ΔpA)、观测井水密度取值误差(Δρ)和观测井点重力加速度取值误差(Δg)。其中,Δp、ΔpA与仪器元器件的性能、工艺有关,Δρ和Δg则是仪器标定设置的重力加速度及水密度与仪器所在的观测井点重力加速度及井水密度的差异造成。
间接测量的观测误差可以按照代数和法[7-8]进行合成。对式(1)求偏微分,水位仪的观测误差(ΔH)可以表示为:
| $ \begin{array}{l} \Delta H = \Delta {H_\rho } + \Delta {H_g} + \Delta {H_P} + \Delta {H_P}_A = {\rm{ }}\\ \frac{H}{\rho }{\rm{ }}\cdot\Delta \rho + {\rm{ }}\frac{H}{g}{\rm{ }}\cdot\Delta g + \frac{1}{{\rho g}}{\rm{ }}\cdot\Delta p + \frac{1}{{\rho g}}\Delta {p_A} \end{array} $ | (3) |
从式(3)可以看出,水位仪压力(包括水柱压力和大气压)测量误差与水柱高度无关,而密度与重力加速度引起的误差则与水柱高度有关。
通常,密度与重力加速度默认为厂家标定环境的密度与重力加速度。目前,我国地震井水位观测网使用的水位仪的重力加速度出厂设置为9.801 5 m/s2,密度设置为1 g/cm3,现场安装时一般不修改。
据最新统计,我国地震井水位观测网共计有508个观测站,水位传感器一般投放在水面以下5 m以内的深度。约80%的观测井水位年变幅小于3 m,大于5 m的观测井基本上分布在京津冀地区。
2.1 重力加速度不考虑压力测量和密度ρ取值的误差,假定仪器测得的水柱高度为H,根据式(3),水位观测误差可以表示为:
| $ \Delta H = \frac{H}{g}\cdot\Delta g $ | (4) |
重力加速度主要与纬度、海拔高程有关。全国观测井所在地重力加速度变化范围为9.779 9~9.806 6 m/s2,变幅较小,最大值在黑龙江,最小值在西藏。
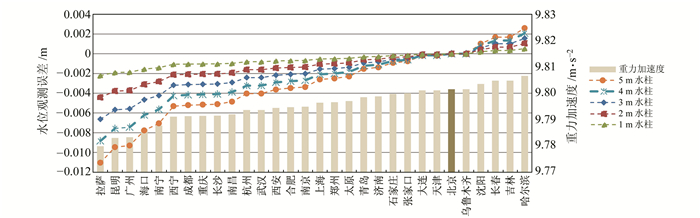
根据式(4),选取观测井分布区域中的31个城市,计算因其重力加速度与仪器出厂的重力加速度差异,在水位仪器观测的水柱高度分别为1 m、2 m、3 m、4 m、5 m时引起的观测误差,计算结果如图 2所示。
|
图 2 重力加速度变化与水位观测误差的关系 Fig. 2 Relationship between gravity acceleration variation and water level observation error |
计算结果表明,当水柱高度为1 m时,重力加速度取值误差引起的最大水位误差为0.002 2 m;为2 m时,最大水位误差为0.004 4 m;为3 m时,最大水位误差为0.006 6 m;为4 m时,最大水位误差为0.008 8 m;为5 m时,最大水位误差为0.011 m。
当水柱高度为1~5 m时,除西藏地区外,其他地区引起的水位观测误差均小于1 cm,特别是水位观测井密集的北京、天津、河北、山东、辽宁等地区的观测误差较小,均不大于2 mm。而西藏目前只有拉萨一口观测井,其年最大变幅在1 m左右,引起的观测误差仅为2~3 mm。
2.2 井水密度井水密度主要受井水矿化度、气水比、水温等因素的影响。根据地震地下流体水位台站建设标准[9],井水矿化度一般要求小于3 g/L。对井水温度高于40 ℃的自流井,设副井管装置进行降温处理。经过降温处理后,井水位观测井筒水温一般在40 ℃以下,且气泡含量很小。因此,在对我国地震井水位观测网中的井水位观测误差分析时,只考虑水温对井水密度的影响,变化范围为0~40 ℃。
不考虑重力加速度g的取值误差,假定仪器测得的水柱高度为H,井水密度为ρ,对应的观测误差可以表示为:
| $ \Delta H = \frac{H}{\rho }\cdot\Delta \rho $ | (5) |
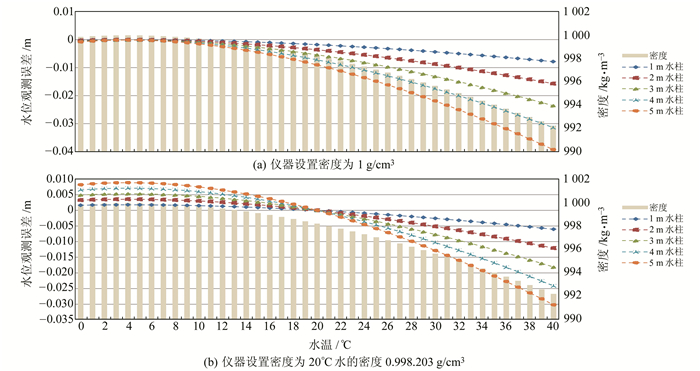
根据1990国际温标水密度表[10]查得0~40 ℃水的密度,计算因其密度与仪器出厂密度(1 g/cm3)的差异,在水位仪器观测的水柱高度分别为1 m、2 m、3 m、4 m、5 m时引起的观测误差,计算结果如图 3(a)所示。
|
图 3 水温引起的水密度变化与水位观测误差关系 Fig. 3 The relationship of water density change and water level observation error caused by water temperature |
从计算结果来看,0~10 ℃的观测误差很小,均小于1 mm,且随着温度的升高,观测误差明显增大。当水柱高度为1~3 m、水温小于28 ℃时,水位观测误差小于1 cm;当水柱高度为3 m、水温大于35 ℃时,出现大于2 cm的误差;当水柱高度为4 m、5 m,水温大于30 ℃时,即出现超过2 cm的误差。
将仪器出厂密度设置为水温20 ℃的水密度值(0.998 203 g/cm3),计算结果如图 3(b)所示。0~10 ℃的观测误差略有增加,但不超过1 cm;20~40 ℃的观测误差则有所减小。当水柱高度为1~5 m、水温小于30 ℃时,观测误差小于1 cm。观测误差大于2 cm只出现在水柱高度为4~5 m、水温大于35 ℃的情形。
据初步统计,我国地震水位观测网的水位观测井筒中水温基本在4~30 ℃范围内,水温常年比较稳定,大部分观测井的水位年最大变幅小于3 m,水位的观测误差不大于1 cm。对于少数水温大于30 ℃、年变幅度较大的非自流井,水位观测误差不容忽视。
3 测试方法水位仪的招标测试与入网测试中,常用的观测误差测试方法主要有两种:模拟井孔法和压力输入法。根据规程[11],最大观测误差不大于0.2%FS。
3.1 模拟井孔法选用长度11~12 m、内径65~110 mm、一端封闭的透明管材,开口朝上竖立,注满水作为模拟井孔。以水位传感器压力敏感元件位置为基点0 m,依次在探头电缆上做好1 m、2 m、3 m、…10 m标志,通过调节水位传感器的位置进行测试。
1) 去程测试:将水位传感器依次下放至模拟井口以下1 m、2 m、3 m、…9 m、10 m处,停留3~5 min,稳定后记录仪器测量值。
2) 回程测试:将水位传感器依次上提至模拟井口以下9 m、8 m、7 m、…2 m、1 m处,停留3~5 min,稳定后记录仪器测量值。
计算每个测量点仪器测量值与实际水位值的误差,最大观测误差在0.2%FS以下,认为该仪器观测误差指标合格。
以某中标仪器#1和#2为例,测试结果如表 1所示。仪器#1去程、回程观测误差均在0.2%FS之内,观测误差指标合格。仪器#2去程的8~10 m、回程的4~10 m,观测误差大于0.2%FS,其他观测误差在0.2%FS之内,观测误差指标不合格。
|
|
表 1 模拟井孔中两套测试仪器观测误差测试记录 Tab. 1 The observation error test record of two sets of testing instruments in simulated well bore |
采用气体作为加压源,压力控制器控制输入压力大小,测试设备连接如图 4所示。通过压力控制器依次给水位传感器施加1、2、3、4、5、6、7、8、9、10 m水柱高度压力,然后卸压依次为9、8、7、6、5、4、3、2、1 m水柱高度压力(压力换算为水柱高度时g取9.801 5 m/s2,水密度取998.203 kg/m3(相当于水温20 ℃的纯水密度)),通过水位仪器主机读取水位值,计算其观测误差。

|
图 4 水位仪观测误差测试设备连接方法 Fig. 4 Schematic diagram of test equipment connection method for water level meter |
计算每个测量点仪器测量值与实际压力值换算得到的水柱高度的误差,最大误差不大于0.2%FS则认为该仪器观测误差指标合格。
对于差压式水位仪,只需要对水位传感器的观测误差进行测试;而对于绝压式水位仪,则还需要对气压传感器的观测误差进行测试。气压传感器的测试方法与水位传感器类似,施压与卸压在相当于4~12 m水柱高度的压力范围内即可。
3.3 测试方法讨论模拟井孔法是对水位仪观测误差的直接测量,反映了在测试环境下水位仪在观测井中不同水柱高度下的观测误差水平。缺点是传感器投放深度误差较大,难以控制。在测试中经常发现,观测误差过大是由于探头电缆长度刻度误差过大而使传感器投放深度不准确所致。从表 1中也发现,同一套仪器回程误差普遍比去程误差要大,反映了人工操作下放、提升传感器也会带来误差。此外,模拟井孔通常只能选在户外,水温受气温影响波动较大也会造成一定误差。
压力输入法是一种间接测量方法,实质是水位仪压力传感器的压力观测误差测试,根据预设的密度和重力加速度来计算水位观测误差,其操作简单,操作误差几乎可以忽略,不受场地影响。
4 结语综上所述,对于我国地震井水位观测网,重力加速度的取值误差对水位观测误差的影响可以忽略,而大部分观测井水温引起的密度取值误差对井水位观测误差的影响基本在允许范围内。水位传感器投放深度越深,密度与重力加速度取值误差引起的水位观测误差越大,其中密度的取值误差影响更为明显。因此,建议水位传感器位置不宜过深,当水温大于28 ℃时,传感器宜放置在水面以下3 m以内,以减少观测误差。水位测量井筒水温不宜超过30 ℃,超过30 ℃的自流井应增设副管进行降温处理,否则需要厂家修改密度参数并重新标定仪器。选择一个合理、适中的水密度值,可以减少整个井水位观测网因密度取值带来的观测误差。
此外,对于少数矿化度较高、水温较高的非自流井,矿化度、水温对水密度的影响不容忽视,要求水位仪标定时必须考虑实际观测井水密度的问题,否则会引起较大的观测误差。对于个别富含气体的井,水气比对水密度的影响更为显著,可能需要将传感器投放到较深的部位或采用其他类型的仪器进行水位观测。
在条件许可的情况下,观测误差采用压力输入法与模拟井孔法相结合进行测试更为全面、准确。对于出厂检测或抽测,可以采用压力输入法进行全量程的观测误差测试,采用模拟井孔法测试仪器在其中某测量范围(如水柱高度2~5 m)的观测误差,既可以检测仪器全量程范围内的观测误差,又可以检查密度和重力加速度的取值是否合理。对于台站测试,则可以采用多深度校测来检查仪器的观测误差。
| [1] |
汪成民. 中国地震地下水动态观测网[M]. 北京: 地震出版社, 1990 (Wang Chengmin. China Earthquake Ground Water Dynamic Observation Network[M]. Beijing: Seismological Press, 1990)
(  0) 0) |
| [2] |
刘春国, 孔令昌, 杨竹转, 等. 我国地震前兆观测井水位观测网监测效能评估分析[J]. 中国地震, 2015, 31(2): 329-337 (Liu Chunguo, Kong Lingchang, Yang Zhuzhuan, et al. Monitoring Efficiency Evaluation of Well-Water-Level Observation Network in China[J]. Earthauqke Research in China, 2015, 31(2): 329-337)
(  0) 0) |
| [3] |
车用太, 王吉易, 李一兵, 等. 首都圈地下流体监测与地震预测[M]. 北京: 气象出版社, 2004 (Che Yongtai, Wang Jiyi, Li Yibing, et al. Underground Fluid Monitoring and Earthquake Prediction in the Capital Circle[M]. Beijing: Meteorological Press, 2004)
(  0) 0) |
| [4] |
杨鼎鸿, 程庆斌, 邓聪, 等. 数字化水位观测仪零漂分析[J]. 地震地磁观测与研究, 2013, 34(3): 144-149 (Yang Dinghong, Cheng Qingbin, Deng Cong, et al. The Zero Drift Problems and Technical Analysis of Digital Water Level Observation[J]. Seismological and Geomagnetic Observation and Research, 2013, 34(3): 144-149)
(  0) 0) |
| [5] |
中国地震局监测预报司. 地下流体数字观测技术[M]. 北京: 地震出版社, 2002 (Secretary of Earthquake Monitoring and Prediction, CEA. Digital Observation Techniques of Underground Fluid[M]. Beijing: Seismological Press, 2002)
(  0) 0) |
| [6] |
何案华, 贾鸿飞, 王宝琐, 等. SWY-Ⅱ型水位仪的研制[J]. 大地测量与地球动力学, 2012, 32(6): 156-159 (He Anhua, Jia Hongfei, Wang Baosuo, et al. Development of SWY-Ⅱ Water Level Meter[J]. Journal of Geodesy and Geodynamics, 2012, 32(6): 156-159)
(  0) 0) |
| [7] |
吴石林, 张玘. 误差分析与数据处理[M]. 北京: 清华大学出版社, 2010 (Wu Shilin, Zhang Qi. Error Analysis and Data Processing[M]. Beijing: Tsinghua University Press, 2010)
(  0) 0) |
| [8] |
孙翼, 王其柳. 安德拉水位计测量中水位值计算的误差分析和估算[J]. 海洋科学进展, 1991(1): 56-60 (Sun Yi, Wang Qiliu. Error Analysis and Assesment in the Computation of Water-Level Values Obtained by Aanderaa Water Level Recorder[J]. Advances in Marine Science, 1991(1): 56-60)
(  0) 0) |
| [9] |
中国地震局. 地震台站建设规范地下流体台站第1部分: 水位和水温台站(DB/T 20. 1-2006)[S]. 北京: 地震出版社, 2006 (CEA. Specification for the Construction of Seismic Station Underground Fluid Station Part1: Water Level and Water Temperature Observatory(DB/T 20. 1-2006)[S]. Beijing: Seismological Press, 2006)
(  0) 0) |
| [10] |
周湄生. 最新温标纯水密度表[J]. 计量技术, 2000(3): 40-42 (Zhou Meisheng. The Realization of the New Water Density Table[J]. Measurement Technique, 2000(3): 40-42)
(  0) 0) |
| [11] |
中国地震局. 中国地震前兆台网技术规程(JSGC-02)[S]. 北京: 地震出版社, 2005 (CEA. Stipulation on Geoscience Observatory Network in China(JSGC-02) [S]. Beijing: Seismological Press, 2005)
(  0) 0) |
2. Institute of Crustal Dynamics, CEA, 1 Anningzhuang Road, Beijing 100085, China
 2018, Vol. 38
2018, Vol. 38

